Вместо предисловия
Урок русского языка вгрузинскойнерусской школе.
Учительница:
— Дэти, это нэльзя понять, это надо запомнить: ОТ ВАС пишется раздельно, а
КВАС — вместе.
Анекдот взят тут.
Введение
На написание статьи вдохновила игра «Wesnoth» — пошаговая стратегия с элементами RPG. В этой игре персонажи перемещаются по карте, состоящей из шестиугольных полигонов. Таким образом, окруженный со всех сторон персонаж может быть атакован шестью вражескими. По этой причине тактическая составляющая в игре очень важна. Возник вопрос: как повлияет на игровой процесс переход от карты с фиксированной геометрией полигонов на карту с произвольной геометрией?
В данном посте решил написать о возможности использования «диаграммы Вороного» в качестве случайной игровой карты. Описаний алгоритмов для построения диаграммы Вороного в сети нашел несколько. Но все, что довелось прочитать мне, либо слишком поверхностны, либо написаны академическим языком. В общем, описания, пригодного для немедленной реализации алгоритма я не нашел. Пришлось начинать реализацию не имея четкого понимания всех тонкостей алгоритма. Нашел в сети исходники на разных языках, но для перевода на нужный мне язык и адаптации под мою задачу все равно не хватало знаний. Поэтому решился изобретать велосипед «с чуть более круглыми колесами и с седушкой помягше».
Возможно кто-то из читателей встречал описание подобной задачи с исходными кодами. Тогда оставьте, пожалуста, в комментариях ссылку — сравним с тем, что получилось у меня.
Алгоритм
Итак… серия «на пальцах» продолжается. Вы можете почитать по-русски про диаграмму Вороного в википедии [1]. Суть такова, что для случайного набора точек (центров) на плоскости (я для простоты рассматриваю 2D-случай) эта диаграмма представляет собой совокупность таких полигонов, что все точки внутри полигона находятся ближе к его «центру», чем к «центрам» других полигонов. Соответственно, все точки на границе между двумя полигонами располагаются на одинаковых расстояниях от обоих центров, а вершины полигонов равноудалены сразу от трех или даже более центров.
Самым «простым» способом построения диаграммы является построение «серединных перпендикуляров» между всеми центрами, т.е. перпендикуляров к отрезкам, соединяющим пары центров, размещенных в середине этих отрезков. Затем нужно найти точки пересечения полученных перпендикуляров и произвести отсечения. Однако вычислений при это нужно будет сделать больше всего (O(n^2 * log n)).
Есть алгоритм т.н. «заметающей прямой» (sweep line, fortune's algorithm [2]). Его вычислительная сложность O(nlogn). Он и будет описан ниже.
Суть алгоритма
В основе этого алгоритма лежит применение вспомогательного объекта — заметающей прямой (ЗП). Она может быть вертикальной или горизонтальной. Я использую горизонтальную ЗМ, движущуюся от бОльших значений Y к меньшим.
Суть в том, что при каждом положении ЗП рассматриваются лишь точки выше этой линии и непосредственно на ней. При этом для каждого из «центрОв» строится парабола, точки на которой равноудалены от «центра» и от ЗП. В данном случае «центры» являются фокусами соответствующих им парабол, а ЗП — директриса этих же парабол.
Уравнение параболы имеет вид:
y = ((x - xf)^2 +yf^2 - L^2)/(2*(yf - L))
где xf, yf — координаты фокуса параболы (центр полигона Вороного);
L — положение ЗП (координата Y текущего обрабатываемого события).
Если построить огибающую снизу всех парабол, то получится т.н. «береговая линия» (beach line). Эта кусочная кривая играет ключевую роль в алгоритме. Точки пересечения «кусков парабол» (назовем их брейкпоинтами) лежат на границах полигонов диаграммы. Когда сходятся в одну точку два брейкпоинта, то одна из «арок» (кусок одной из парабол) «схлопывается», т.е. две соседние к ней арки соединяются друг с другом. При этом образуется вершина полигона диаграммы.
Таким образом, задача сводится к детектированию и обработке двух событий — добавления в список рассматриваемых центров новой точки (site event) и подозрение на наличие вершины (circle event) [3]. И так далее… примерно такое описалово я и находил в сети на разных языках. И на данном, концептуальном, уровне все выглядет не очень сложно. Но как именно (по шагам) осуществляется детектирование? И что именно делать с этими событиями?
Попробую изложить простыми словами.
Структура данных
Как было сказано выше, в алгоритме ключевыми объектами являются события: событие точки (site event) и событие круга (circle event). Эти события помещаются в список, который сортируется в моем случае по убыванию координаты Y, т.е. события имеющие бОльшие значения координаты Y размещаются выше в очереди и обрабатываются раньше. Таким образом, первое, что нам понадобится — упорядоченный список для хранения событий.
Второе, что нам понадобится — бинарное дерево. В этом дереве будут размещены узлы трех типов: Arc — арка (часть параболы), этот узел должен хранить координаты фокуса параболы и ссылку на событие круга, если таковое имеется; BP — breakpoint, точка пересечения двух парабол; BPOwner — корень поддерева, его детьми являются узлы типа BP. Узлы BP и BPOwner должны хранить ссылку на грань. Нужно обязательно хранить грани в отдельном списке, т.к. узлы BP и BPOwner будут удаляться при обработке событий круга.
Соответствие узлам Arc и BP вы легко найдете в публикации [6]. BPOwner прямого наименования не имеет — просто корень поддерева. Я дал ему наименование лишь для удобства программной реализации.
Типичная схема бинарного дерева для диаграммы Вороного (как я ее себе представляю) изображена на рис. 1.
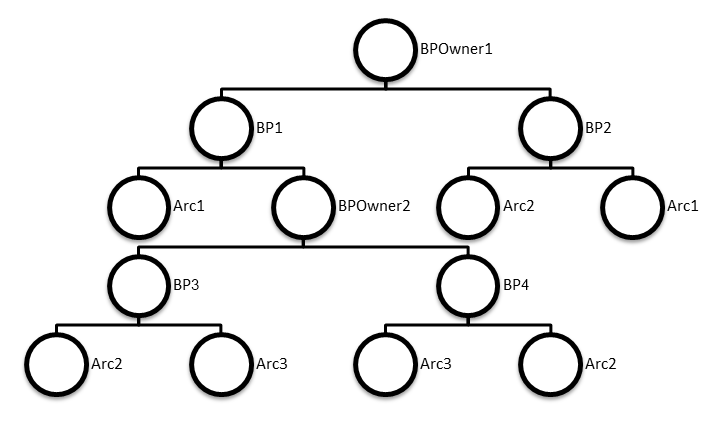
Рис. 1. Бинарное дерево.
На этом рисунке сразу можно выделить потенциально имеющееся событие круга. Если смотреть слева, то Arc1, Arc2, Arc3 образуют тройку фокусов, которые с большой вероятностью не будут лежать на одной прямой. Больше событию круга возникнуть негде, т.к. остаются тройки {Arc3 Arc3 Arc2}, {Arc3 Arc2 Arc2} и {Arc2 Arc2 Arc1}. Такая схема построения дерева пусть и избыточна, но проста в анализе.
Подробнее структуру данных можно изучить в [6]. Возможно мое изложение отличается от представленного в той публикации, но для меня так проще.
Главный цикл
- Инициализация данных.
- Пока очередь НЕ ПУСТА:
- Вырезать из очереди первое событие (с наибольшим значением координаты Y)
- If(event = = Site Event)
ProcessSite(event) - Else
ProcessCircle(event)
- Финишировать все грани, ссылки на которые имеются в бинарном дереве.
Действительно просто. Вся магия в обработчиках событий.
Обработка «события точки»
Что такое событие точки для нашего бинарного дерева? Когда ЗП попадает на очередную точку, то в дерево добавляется новая парабола. Нужно заметить, что, во-первых, по алгоритму ЗП перемещается от события к событию (в демо-анимациях к алгоритму эта прямая движется плавно), а во-вторых, изначально парабола представляет собой вертикально направленный луч. В месте пересечения этого луча с одной из парабол образуется сразу два «брейкпоинта» (BP). Таким образом, для каждого события точки в дереве находится парабола с которой произойдет пересечение соответствующего луча. Сделать это легко методом спуска, начиная с корня всего дерева и сравнивая координаты X этого события и узлов BPOwner и BP. Спуск происходит до тех пор пока не встретится арка. Если арка содержит ссылку на существующее в очереди событие круга, то нужно удалить это событие из очереди и удалить ссылки на это событие из данной арки и ее соседей, арки справа и слева. Далее вместо арки (см. Arc1 ниже) создается поддерево вида:
BPOwner
/ \
BP BP
/ \ / \
Arc1 Arc2 Arc2 Arc1Теперь, когда структура дерева поменялась, следует пробежать по дереву слева направо в поисках событий круга. Для этого нужно брать последовательно тройки арок и проверять координаты фокусов соответствующих им парабол на колинеарность. Если три фокуса не лежат на одной прямой, то можно построить общую для них окружность. Если нижняя точка этой окружности лежит ниже ЗП, то можно добавить в очередь событие круга. Нижняя точка окружности — это место, где событие произойдет, а центр — это точка, где будет находиться вершина полигона Вороного.
Подводя итог скажу, что события точек только добавляют узлы в дерево и события круга в очередь событий. Больше ничего при их возникновении не делается. При наступлении события точки даже не производится вычисление координат BP — точек пересечения парабол. «Главная магия» делается в обработчике событий круга.
Обработка «события круга»
Каждое событие круга должно содержать ссылку на арку, которая будет удалена («схлопнется», см. выше) при наступлении этого события. Ранее было написано, что для детектирования события круга рассматриваются тройки арок. Так вот, в событии круга должна храниться ссылка на среднюю арку, т.е. на ту, у которой значение координаты X находится между соответствующими значениями двух других арок. В этих соседних арках также должна храниться ссылка на то же событие круга, что и у средней. Хотя особой необходимости я в этом не вижу. Мне, как «на-палечнику», проще записать в среднюю арку ссылки на две соседние арки — левую и правую. Благодаря этому не придется прогуливаться по дереву в поисках соседней ветки с нужной аркой (обязательно одна из оставшихся двух арок будет в соседней ветке, т.к. дерево бинарное).
Обработка события круга будет заключаться в обновлении координат брейкпоинтов, непосредственно ограничивающих удаляемую арку. Далее производится удаление арки и двух, связанных с ней брейкпоинтов. После этого нужно перестроить дерево. В результате будет добавлен новый узел BP, а получившееся поддерево переместится на уровень выше…
Текстом такие процедуры воспринимаются достаточно трудно. Во всяком случае для меня, как человека без серьезных знаний в теории графов и бинарных деревьев, это было нетривиальной задачей, поэтому привожу еще и иллюстрацию на рис. 2.
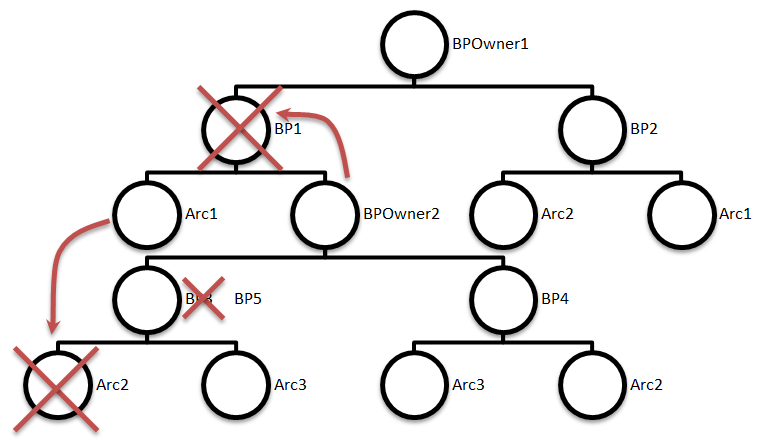
Рис. 2 Обработка события круга
Результат
Здесь я приведу характерный вид диаграммы, т.е. вид игровой карты с произвольной полигональной геометрией.

Рис.3 Игровая карта
На этой карте в «центрАх» (напомню — это исходный набор случайно распределенных по площади точек) могут находиться персонажи. Через грани этих полигонов на персонажа может напасть персонаж противника. На представленном выше рисунке «зеленый человечик» обозначает… нет не алкоголизм. Полигон, в котором размещен силуэт зеленого цвета — безопасная локация с точки зрения количества возможнах атак за ход противника (4 максимум). А вот персонажу красного цвета не повезло. На него может быть совершено максимум 8 нападений со стороны недружественного населения.
Тактика
Каждому полигону на карте можно присвоить «стоимость прохождения». Можно поступить иначе — назначить «стоимость пересечения» границам полигонов или использовать комбинацию того и другого (стоимость пересечения границы + половина стоимости прохождения). Также, в зависимости от площади полигона (или количества охвачиваемых точек координатной сетки карты), можно назначить различные бонусы (периодичность рождения артефактов, происхождения каких-либо событий и пр.), очки защиты, ресурсы постройки укреплений и т.д. Это уже предоставляет большие тактические возможности. Плюс к этому следует правильно выбирать полигон, в котором можно остановиться. Как написано в начале, большой полигон может иметь большее количество границ, а значит и большее число нападений за один ход противника. Однако большой полигон — это большие бонусы (при условии назначения бонусов в зависимости от площади, а не от количества границ). Значит особо ценными будут полигоны с максимальной площадью при минимальном количестве границ. Вот такая задача «МаксиМин», которую нетрудно автоматизировать. Труднее автоматизировать успешное использование получаемых бонусов для ИИ.
Поиск пути можно осуществлять с использованием A* («TODO» для отдельного поста). Можно ввести систему прокладки путей — сначала проводится персонаж вручную, делается запись пути, а потом можно использовать созданные «waypoint'ы» для автоматизации. Но это будет скорее всего слишком неудобно. На геймплее может сказаться негативно.
Теперь об укреплениях. У каждого полигона должен быть некий набор ресурсов для создания укреплений, от которых будет зависеть тип фортификации и скорость возведения сооружений. Прямо «Цивилизация» получается. На укрепление в выбранной позиции персонаж тратит очки действий. Их можно разделить на две группы — защитные и атакующие. При этом зашитные ОД тратятся на постройку укреплений и оборонительную активность во время атаки противника (поднять щит, увернуться от стрелы, блокировать атаку и пр.), а атакующие могут быть потрачены как в стадии атаки, так и при защите (контратака, обезоруживание). Тут можно упомянуть ZPG «MyBrute», в которой аватарчик может при защите перехватить инициативы и атаковать в ответ, не получив удара от противника.
Каждый персонаж может иметь набор укреплений, постройке которых он обучен. Каждый тип укреплений дает разную степень защищенности и/или бонусы. Помимо бонусов от укреплений, сам полигон может давать случайные бонусы. Пребывая долгое время в данном месте, персонаж увеличивает вероятность найти что-то ценное или «открыть» некое скрытое свойство данного полигона.
Можно и дальше продолжать такие рассуждения. Пространства для маневров предостаточно, но тогда мы отклонимся от темы статьи.
Выводы
Смена геометрии игровой карты неминуемо приведет к серьезным изменениям (думаю в лучшую сторону) в тактике игры. Появится дополнительный тактический уровень, возможность при правильном подходе в переломный момент битвы перевесить чашу весов в свою сторону. К тому же, такой подход позволит сделать игровую карту динамической — видоизменять ее топологию (локально или глобально). Тут нельзя не вспомнить не реализованную до конца (на мой взгляд) задумку изменяемых локаций в играх «S.T.A.L.K.E.R.». В 2D это реализовать не очень сложно. Но не забываем о том, что диаграмма Вороного строится и для 3D.
Спасибо за внимание! Ваши комментарии…