Введение
В 1965 г. в журнале «Information and Control» была опубликована работа Л.Заде под названием «Fuzzy sets». Это название переведено на русский язык как нечеткие множества. Побудительным мотивом стала необходимость описания таких явлений и понятий, которые имеют многозначным и неточный характер. Известные до этого математические методы, использовавшие классическую теорию множеств и двузначную логику, не позволяли решать проблемы этого типа.
При помощи нечетких множеств можно формально определить неточные и многозначные понятия, такие как «высокая температура» или «большой город». Для формулирования определения нечеткого множества необходимо задать так называемую област рассуждений. Например, когда мы оцениваем скорость автомобиля, мы ограничимся диапазоном X = [0, Vmax], где Vmax — максимальная скорость, которую может развить автомобиль. Необходимо помнить, что X — четкое множество.
Основные понятия
Нечетким множеством A в некотором непустом пространстве X называется множество пар

где

— функция принадлежности нечеткого множества A. Эта функция приписывает каждому элементу x степень его принадлежности нечеткому множеству A.
Продолжив предыдущий пример, рассмотрим три неточные формулировки:
— «Малая скорость автомобиля»;
— «Средняя скорость автомобиля»;
— «Большая скорость автомобиля».
На рисунке представлены нечеткие множества, соответствующие приведенным формулировкам, с помощью функций принадлежности.

В фиксированной точке X=40км/ч. функция принадлежности нечеткого множества «малая скорость автомобиля» принимает значением 0,5. Такое же значение принимает функция принадлежностинечеткого множества «средняя скорость автомобиля», тогда как для множества «большая скорость автомобиля» значение функции в этой точке равно 0.
Функция T двух переменных T: [0, 1] x [0, 1] -> [0, 1] называется T-нормой, если:
— является не возрастающей относительно обоих аргументов: T(a, c) < T(b, d) для a < b, c < d;
— является коммутативной: T(a, b) = T(b, a);
— удовлетворяет условию связности: T(T(a, b), c) = T(a, T(b, c));
— удовлетворяет граничным условиям: T(a, 0) = 0, T(a, 1) = a.
Прямой нечеткий вывод
Под нечетким выводом понимается процесс, при котором из нечетких посылок получают некоторые следствия, возможно, тоже нечеткие. Приближенные рассуждения лежат в основе способности человека понимать естественный язык, разбирать почерк, играть в игры, требующие умственных усилий, в общем, принимать решения в сложной и не полностью определенной среде. Эта способность рассуждений в качественных, неточных терминах отличает интеллект человека от интеллекта вычислительной машины.
Основным правилом вывода в традиционной логике является правило modus ponens, согласно которому мы судим об истинности высказывания B по истинности высказываний A и A -> B. Например, если A — высказывание «Степан — космонавт», B — высказывание «Степан летает в космос», то если истинны высказывания «Степан — космонавт» и «Если Степан — космнавт, то он летает в космос», то истинно и высказывание «Степан летает в космос».
Однако, в отличие от традиционной логики, главным инструментом нечеткой логики будет не правило modus ponens, а так называемое композиционное правило вывода, весьма частным случаем которого является правило modus ponens.
Предположим, что имеется кривая y=f(x) и задано значение x=a. Тогда из того, что y=f(x) и x=a, мы можем заключить, что y=b=f(a).
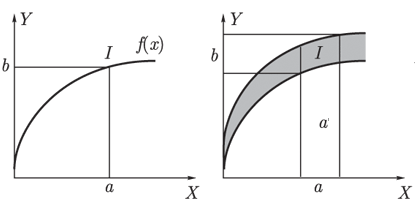
Обобщим теперь этот процесс, предположив, что a — интервал, а f(x) — функция, значения которой суть интервалы. В этом случае, чтобы найти интервал y=b, соответствующий интервалу a, мы сначала построим множество a' с основанием a и найдем его пересечение I с кривой, значения которой суть интервалы. Затем спроектируем это пересечение на ось OY и получим желаемое значение y в виде интервала b. Таким образом, из того, что y=f(x) и x=A — нечеткое подмножество оси OX, мы получаем значение y в виде нечеткого подмножества B оси OY.
Пусть U и V — два универсальных множества с базовыми переменными u и v, соответственно. Пусть A и F — нечеткие подмножества множеств U и U x V. Тогда композиционное правило вывода утверждает, что из нечетких множеств A и F следует нечеткое множество B = A * F.
Пусть A и B — нечеткие высказывания и m(A), m(B) — соответствующие им функции принадлежности. Тогда импликации A -> B будет соответствовать некоторая функция принадлежности m(A -> B). По аналогии с традиционной логикой, можно предположить, что

Тогда
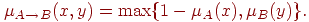
Однако, это не единственное обобщение оператора импликации, существуют и другие.
Реализация
Для реализации метода прямого нечеткого логического вывода нам понадобится выбрать оператор импликации и T-норму.
Пуская T-норма будет функция минимума:
- def t_norm(v1, v2):
- return min(v1, v2)
а оператором импликации будет функция Гёделя:
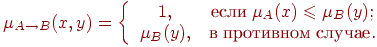
- def impl(v1, v2):
- '''<br/> Godel implication<br/> '''
- if v1 <= v2:
- return 1.0
- else:
- return v2
Входные данные будут содержать знания (нечеткие множества) и правила (импликации), например:
A = {(x1, 0.0), (x2, 0.2), (x3, 0.7), (x4, 1.0)}.
B = {(x1, 0.7), (x2, 0.4), (x3, 1.0), (x4, 0.1)}.
A => B.
Импликация будет представлена в виде декартовой матрицы, каждый элемент которой рассчитывается с помощью выбранного оператора импликации (в данном примере — функции Гёделя):
- def compute_impl(set1, set2):
- '''<br/> Computing implication<br/> '''
- relation = {}
- for i in set1.items():
- relation[i] = {}
- for j in set2.items():
- v1 = set1.value(i)
- v2 = set2.value(j)
- relation[i][j] = impl(v1, v2)
- return relation
Для данных выше это будет:
Conclusion:
A => B.
x1 x2 x3 x4
x1 1.0 1.0 1.0 1.0
x2 1.0 1.0 1.0 0.1
x3 1.0 0.4 1.0 0.1
x4 0.7 0.4 1.0 0.1
Далее в результате вывода получается новое множество:
- def conclusion(set, relation):
- '''<br/> Conclusion <br/> '''
- conl_set = []
- for i in relation:
- l = []
- for j in relation[i]:
- v_set = set.value(i)
- v_impl = relation[i][j]
- l.append(t_norm(v_set, v_impl))
- value = max(l)
- conl_set.append((i, value))
- return conl_set
Результат:
B' = {(x1, 1.0), (x2, 0.7), (x3, 1.0), (x4, 0.7)}.
Источники
- Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского. — М.: Горячая линия — Телеком, 2006. — 452 с.: ил.
- Zadeh L. A. Fuzzy Sets, Information and Control, 1965, vol. 8, s. 338-353