Facebook Hacker Cup 2011 проходит в 4 раунда — квалификационный, два онлайн раунда и финальный, в главном офисе.
Квалификационный раунд, анонсированный официально Хабром завершился успешно.
Результаты раунда говорят о 5846 игроках, прошедших в первый онлайн тур.
Участникам квалификационного раунда предлагалось 3 задачи, для прохождения достаточно было правильного решения любой из них.
А вот первый онлайн раунд, прервав ближе к завершению, перенесли из-за технических проблем минимум на неделю:
We've decided to push back the remaining subrounds of round 1 until we are sure that they can run smoothly. Updates will follow here, but you can safely assume that the subrounds will not occur at least until next weekend.
В целях экономии места, перевод условий я сокращу, оставив суть, необходимую для решения. Полные условия доступны в оригинале на английском.
Найти число представлений целого числа в виде суммы двух полныых квадратов целых (например: 10=1^2+3^2 — одно разложение, а 25=5^2+0^2=4^2+3^2 два разных разложения).
На входящие числа:
10 25 3 0 1
Правильный ответ программы:
1 2 0 1 1
На задачу наложено ограничение по времени — отправить ответ нужно до истечения 6 минут с момента скачивания файла заданий, в котором максимум 100 чисел, требующих подсчета числа разложений.
Оценка: корень из 2147483647 равен 46340,95 — не так уж и много.
Идея: заполнить массив полными квадратами от 0 до 46341
тогда задача сведется к пробеганию с двух концов массива вовнутрь:
А пока голова думает, руки успевают набрать кривое решение прямым перебором (обходя массив слева направо и из разности исходного числа и квадрата беря корень).
Приводить код не буду — сэкономим внимание для более интересной задач.
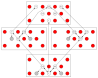
Между двумя стенками в шахматном порядке закреплены шайбы (красные):

С зеленого кружочка падает монетка, которая налетая на шайбу равновероятно отскакивает левее или правее (от крайней шайбы монетка всегда отскакивает вовнутрь). Падая монетка попадет в голубой кружочек — выход. Если монетку кидали в средний кружок, она может путешествовать вдоль любой стрелочки:

Во входящих данных указан размер «поля» — всегда нечетного числа строк, и любого числа столбцов, и номер выхода, в который нужно попасть монеткой.
За ответ принимают номер окна и вероятность, с которой монетка попадет в заданный выход с наибольшей вероятностью.
Помимо этого, некоторые шайбы удалены (потерялись от времени).
Будем рассматривать поле поменьше, в котором 1 шайба потерялась, а попасть нужно в средний выход:

Рекурсия с подсчетом всевозможных путей не успеет — максимальный размер поля 99на100 а за отведенные 6 минут нужно успеть просчитать до 100 разных полей, и успеть отправить назад результат.
Ключевая идея:

Идем снизу вверх, от точки выхода — в нее кладем вероятность 1. в нее можем попасть из двух точек, левее-выше и правее-выше. Из этих точек в точку выхода мы попадаем с вероятностью 1/2. Правило сложения вероятностей говорит об их перемножении. Уровень закончили, переходим к следующему: Есть 2 точки, с вероятностями 1/2. Рассматриваем независимо их вклад в следующий:
Теперь складываем (уже по обычному) полученные вероятности, чтобы получить третий слой, который оказывается последним. (Иначе для каждого элемента с ненулевой вероятностью запускаем аналогичный процесс).
Имеем, что в средний выход можно попасть только кидая монетку из среднего или правого окошка, причем с одинаковой вероятностью.
В формате исходных данный фейсбука, рассматриваемое поле представляется строкой: 3 4 1 1 0
Теперь реализуем эту идею:
Переставляя слова данного набора составить слово с наименьшим лексикографическим порядком (как в словаре).
Например, из набора: facebook hacker cup for studious students
Нужно получить слово: cupfacebookforhackerstudentsstudious
(удалил неправильное решение)
Решение от хабраюзера funca, сложность О(N!)
По условию N<=9, факториальная сложность успевает отлично
Плюсовать этот его коммент
Решение от хабраюзера Skiminok сложность O(N log N)
Плюсовать этот его коммент
Более короткая версия на лямбде от funca
Плюсовать этот коммент
Квалификационный раунд, анонсированный официально Хабром завершился успешно.
Результаты раунда говорят о 5846 игроках, прошедших в первый онлайн тур.
Участникам квалификационного раунда предлагалось 3 задачи, для прохождения достаточно было правильного решения любой из них.
А вот первый онлайн раунд, прервав ближе к завершению, перенесли из-за технических проблем минимум на неделю:
We've decided to push back the remaining subrounds of round 1 until we are sure that they can run smoothly. Updates will follow here, but you can safely assume that the subrounds will not occur at least until next weekend.

В целях экономии места, перевод условий я сокращу, оставив суть, необходимую для решения. Полные условия доступны в оригинале на английском.
Задача 1. «Double Squares»
Найти число представлений целого числа в виде суммы двух полныых квадратов целых (например: 10=1^2+3^2 — одно разложение, а 25=5^2+0^2=4^2+3^2 два разных разложения).
- Диапазон входящих чисел от нуля до 2147483647
На входящие числа:
10 25 3 0 1
Правильный ответ программы:
1 2 0 1 1
На задачу наложено ограничение по времени — отправить ответ нужно до истечения 6 минут с момента скачивания файла заданий, в котором максимум 100 чисел, требующих подсчета числа разложений.
Решаем:
Оценка: корень из 2147483647 равен 46340,95 — не так уж и много.
Идея: заполнить массив полными квадратами от 0 до 46341
тогда задача сведется к пробеганию с двух концов массива вовнутрь:
- сумма квадратов больше заданного числа — правую границу сдвигаем влево
- сумма квадратов меньше заданного числа — левую границу сдвигаем вправо
- сумма квадратов равна заданному числу — инкрементируем результат
- границы соединились — выводим ответ, берем следующее число
А пока голова думает, руки успевают набрать кривое решение прямым перебором (обходя массив слева направо и из разности исходного числа и квадрата беря корень).
Приводить код не буду — сэкономим внимание для более интересной задач.
Задача 2. Peg Game
Между двумя стенками в шахматном порядке закреплены шайбы (красные):

С зеленого кружочка падает монетка, которая налетая на шайбу равновероятно отскакивает левее или правее (от крайней шайбы монетка всегда отскакивает вовнутрь). Падая монетка попадет в голубой кружочек — выход. Если монетку кидали в средний кружок, она может путешествовать вдоль любой стрелочки:

Во входящих данных указан размер «поля» — всегда нечетного числа строк, и любого числа столбцов, и номер выхода, в который нужно попасть монеткой.
За ответ принимают номер окна и вероятность, с которой монетка попадет в заданный выход с наибольшей вероятностью.
Помимо этого, некоторые шайбы удалены (потерялись от времени).
Будем рассматривать поле поменьше, в котором 1 шайба потерялась, а попасть нужно в средний выход:

Решение
Рекурсия с подсчетом всевозможных путей не успеет — максимальный размер поля 99на100 а за отведенные 6 минут нужно успеть просчитать до 100 разных полей, и успеть отправить назад результат.
Ключевая идея:

Идем снизу вверх, от точки выхода — в нее кладем вероятность 1. в нее можем попасть из двух точек, левее-выше и правее-выше. Из этих точек в точку выхода мы попадаем с вероятностью 1/2. Правило сложения вероятностей говорит об их перемножении. Уровень закончили, переходим к следующему: Есть 2 точки, с вероятностями 1/2. Рассматриваем независимо их вклад в следующий:
- В левую точку мы можем попасть только упав справа (сверху шайба), а слева просто пролетим мимо. Из правого «родителя» в нее мы попадаем с 1/2. Опять «складываем» вероятности, т.е. перемножаем 1/2*1/2, получаем 0.25
- В правой точке вероятность прихода от левого родителя 1/2, а от правого — 1, т.к. за игровое поле монетка не выходит — там стенка
Теперь складываем (уже по обычному) полученные вероятности, чтобы получить третий слой, который оказывается последним. (Иначе для каждого элемента с ненулевой вероятностью запускаем аналогичный процесс).
Имеем, что в средний выход можно попасть только кидая монетку из среднего или правого окошка, причем с одинаковой вероятностью.
В формате исходных данный фейсбука, рассматриваемое поле представляется строкой: 3 4 1 1 0
- первые две цифры — размеры поля
- номер выхода (считают с нулевого)
- количество потерянных шайб, такое же количество следующих пар-координат (1 0 означает удаленную первую шайбу из второй строчки)
Теперь реализуем эту идею:
- #!/usr/bin/python
- #coding=utf-8
-
- #ищет "родителей"
- def next(y,x,v):
- l=[]
- if (x+y)%2==0: #где запланирована фишка
- l.append((y-1,x,v))
- return l
- #значит на пустом месте
- if (y-1,x) in skip:#над нами пусто
- l.append((y-1,x,v))
- #но ретернить рано - могли и с боков свалиться
- #проверяем левее
- if x!=0:#не в самом левом столбике
- if x!=0 and x!=size:
- if (y,x-1) not in skip:#левее есть фишка
- if x==1 or (y%2==1 and ( x==2 or x==size)):
- #дополнительные условия - на то, что крестик не скраю
- l.append((y-1,x-1,v))# с самой левой один путь дорога
- else:
- l.append((y-1,x-1,v/2.))# не с самой левой - два пути
- # если в самом левом столбце - падение сверху уже запланировано
- #проверяем правее
- if x!=size:#не в самом правом столбике
- if (y,x+1) not in skip:#правее есть фишка
- if x==size-1 or (y%2==1 and ( x+1==2 or x+1==size-2)):
- l.append((y-1,x+1,v))# с самой правой один путь дорога
- else:
- l.append((y-1,x+1,v/2.))# не с самой правой - два пути
- return l
- #перевод входных данных в сквозную декартову адресацию
- def rc_to_yx(rs,cs):
- if rs%2==0:
- return (rs,cs*2)
- return (rs,cs*2+1)
- f = open('in', 'r')
- f.readline()
- lines_in=f.readlines()
- for inputWords in lines_in:
- skip_l = []
- skip=set(skip_l)
- inputWords = inputWords[0:-1].split(' ')
- inputWords= filter (lambda a: a != "", inputWords)
- r=int(inputWords.pop(0))
- c=int(inputWords.pop(0))
- target=int(inputWords.pop(0))
- s_count=inputWords.pop(0)
- for q in range(int(s_count)):
- rs=inputWords.pop(0)
- cs=inputWords.pop(0)
- skip.add(rc_to_yx(int(rs),int(cs)))
- #Закончили с загрузкой данных, приступаем к вычислениям
- size=c+c-2 #"ширина"слоя, для определения правой границы
- n={}
- n[(r-1,target*2+1)]=1
- for q in range(r-1):
- s=n
- n={}
- for (b,a),v in s.iteritems():
- for (y,x,v) in next(b,a,v):
- try:
- n[(y,x)]+=v
- except KeyError:
- n[(y,x)]=v
- #print n #дебажный послойный вывод
- #Все уже посчитали, осталось вывести максимальную вероятность
- maxv=0
- maxx=0
- for (y,x),v in n.iteritems():
- if v>maxv:
- maxv=v
- maxx=x
- #Выводим, как хочет фейсбук - с 6 нулями
- print '%(i)d %(d)f' % \
- {"i":(maxx-1)/2, "d":maxv}
- print
* This source code was highlighted with Source Code Highlighter.Задача 3. «Studious Student»
Переставляя слова данного набора составить слово с наименьшим лексикографическим порядком (как в словаре).
Например, из набора: facebook hacker cup for studious students
Нужно получить слово: cupfacebookforhackerstudentsstudious
Решение
Решение от хабраюзера funca, сложность О(N!)
- from itertools import permutations
- source = "jibw ji jp bw jibw"
- words = source.split()
- answer = min("".join(combination) for combination in permutations(words))
* This source code was highlighted with Source Code Highlighter.По условию N<=9, факториальная сложность успевает отлично
Плюсовать этот его коммент
Решение от хабраюзера Skiminok сложность O(N log N)
- from functools import cmp_to_key
- def comp(a, b):
- return -1 if a + b < b + a else 1 if a + b > b + a else 0
- def solve(s):
- return "".join(sorted(s.split(), key = cmp_to_key(comp)))
* This source code was highlighted with Source Code Highlighter.Плюсовать этот его коммент
Более короткая версия на лямбде от funca
- def solve(s):
- return "".join(sorted(s.split(), cmp=lambda a, b: cmp(a+b, b+a)))
* This source code was highlighted with Source Code Highlighter.Плюсовать этот коммент