Добрый вечер.
В этом посте я разберу задачу B «Дубы» с практического тура городской олимпиады школьников Санкт-Петербурга по информатике.
Задача эта на динамическое программирование по подотрезкам и идея решения интересна тем, что удобнее посчитать две динамики вместо одной. Если вас заинтересовало (незнание динамики не освобождает, но будет труднее) — добро пожаловать.
Для начала можете посмотреть условие задачи. Оно вместе с тестами лежит тут (только условия можно скачать с min.us).
После откидывания легенды остаётся следующая задача:
Если хотите, можете подумать (название поста может Вам подсказать).
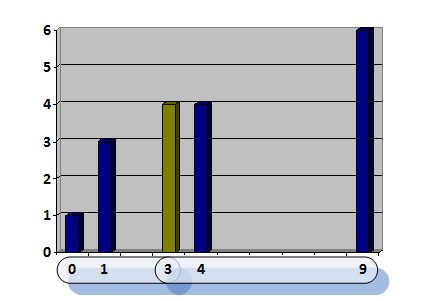
Как можно было догадаться из тегов — решение есть некая динамика. Если Вы забыли или не знали, что такое динамическое программирование, я напомню. Идея динамики в том, что для совсем маленьких примеров (например, одно дерево) ответ очевиден (ничего не пилить), а для больших решение можно получить, зная решения для каких-то более мелких независимых подзадач. В этом месте динамика очень напоминает индукцию. Как же свести задачу, например, для десяти деревьев к меньшим? Предположим, что мы уже знаем ответ (мы не будем этим пользоваться, но это полезно представить). В нём есть два крайних дерева и какая-то середина. Давайте переберём любое дерево из этой середины (вообще любое, которое лежит по высоте между границами — в противном случае его оставлять нельзя):
Можно заметить, что все операции будут производиться либо в левой части, либо в правой. Значит, друг от друга они не зависят никак. Вот и разбили на две независимые подзадачи. Можно прорелаксировать (выбрать лучший) ответ на нашем большом отрезке.
А что делать, когда на отрезке между нашими границами нет деревьев (например, деревья 4 и 9)? Тут мы понимаем, что в таком случае нам нужно срубить все деревья на интервале. Вопрос — в каком порядке? Есть соблазн сделать жадный алгоритм: срубать первое попавшееся дерево и так, пока они не кончатся. Однако он неверен:

Думаю, очевидно, что не стоит придумывать различные оптимизации в стиле «на последних двух шагах запустить перебор» и пр. — это всё обламывается большим случайным тестом.
Нужно что-то поумнее. Смотрим на название поста еще разок и придумываем очень похожуюю динамику по подотрезкам: для двух деревьев и меньше удалять вообще ничего не надо. А для большего количества надо перебрать дерево, которое удалим последним и заметить, что опять получили две подзадачи: слева и справа. Единственный отличающий момент — надо проверить, что это дерево можно будет в конце удалить (когда его соседями станут границы интервала)
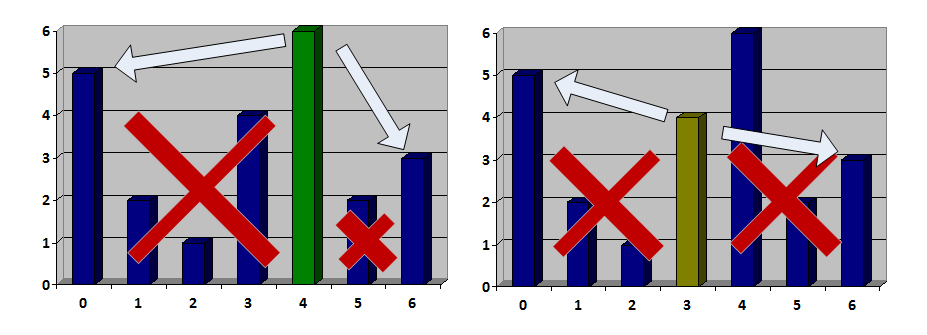
Например, удалить дерево 4 последним можно, а 3 — нельзя.
Ответ восстанавливается классическим методом — запоминаем оптимальный переход из каждого состояния (где достигся самый лучший ответ) в массив, а потом идём с конца. В динамике по подотрезкам восстановление удобно писать рекурсивно:
Всего у нас O(n2) состояний каждой динамики (по одному на каждый подотрезок). В каждой динамике переход производится за O(n) — перебрать дерево внутри интервала. При восстановлении ответа каждое состояние мы посещаем не более одного раза. Получается квадрат, но так это асимпотически (бесконечно меньше на бесконечно больших n) меньше куба, то им можно пренебречь.
Итоговое время работы — O(n3), что при n=200 составляет O(8*106), что отрабатывает мгновенно. Это нас тоже устраивает.
Для начала надо считать данные в массив/вектор. Это Вы делать умеете.
Далее надо подсчитать динамику для удаления всех деревьев. Будем хранить её в массиве int del[a][b] — -1, если невозможно удалить все деревья на интервале (a, b), и номер последнего дерева иначе.
Для перебора подотрезков есть соблазн написать два цикла:
Однако это в корне неверно, посколько переход динамики будет верным только тогда, когда мы знаем ответ для «меньших» подзадач. В нашем случае — для подотрезков меньшей длины. Поэтому надо сначала перебрать длину отрезка, а затем — начало (или конец):
В этом цикле надо перебрать последнее дерево и проверить возможность удаления. Также не следует забывать проинициализировать динамику для пустых интервалов:
Вторую динамику будем хранить в двух массивах — int dyn[a][b] и int fr[a][b]. Первый — собственно, ответ для подотрезка (сколько минимум деревьев надо удалить), или бесконечность (я использую 109), если нельзя оставить неубывающую подпоследовательность. А во втором массиве мы будем хранить либо -1, если в первом записана бесконечность, либо последнее удалённое дерево.
Итак, пишем. Тут можно инициализировать всё по ходу (отдельный цикл нужен только для заполнения бесконечностями):
Оно было уже полностью написано выше — тот код полностью работает. Осталось лишь проверить, что ответ есть, вызвать функцию, и вывести результат:
Всю программу можно просмотреть на pastebin. Так как она писалась на олимпиаде, в ней присутствуют некоторые сокращения для быстрого набора и отсутствуют комментарии. Впрочем, весь значимый код я привёл в статье.
На тему тестирования алгоритмических задач можно написать много больших статей. Но нам же хочется побыстрее, правда же? Поэтому вспоминаем, куда мы скачали тесты в начале статьи, распаковываем их куда-нибудь (задача называется oaks) и либо ручками прогоняем все 50 тестов, либо компилируем файл check.dpr (скомпилированный) и пишем скрипт на CMD:
Запускаем. Если увидели надпись ALL IS OK! и «Нажмите Any key» — ваше решение верное. Если нет — значит есть тест, на котором оно работает неверно. Не спешите смотреть этот тест — гораздо полезнее будет самостоятельно найти и исправить баг.
Вот и всё, что я хотел рассказать. Надеюсь, Вы всё поняли и я не зря потратил Ваше время.
Спасибо за внимание, легких вам Accepted'ов.
Буду рад конструктивной критике.
В этом посте я разберу задачу B «Дубы» с практического тура городской олимпиады школьников Санкт-Петербурга по информатике.
Задача эта на динамическое программирование по подотрезкам и идея решения интересна тем, что удобнее посчитать две динамики вместо одной. Если вас заинтересовало (незнание динамики не освобождает, но будет труднее) — добро пожаловать.
Условие
Для начала можете посмотреть условие задачи. Оно вместе с тестами лежит тут (только условия можно скачать с min.us).
После откидывания легенды остаётся следующая задача:
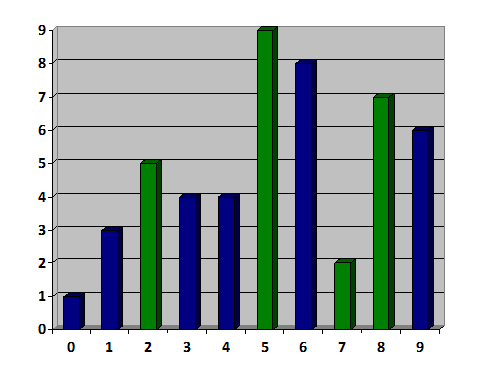
- Имеется n (2<=n<=200) дубов, у каждого есть высота — целое число от 1 до 1000 (вкл.) .
- Мы умеем: удалить дуб из последовательности, если:
- Либо он строго меньше обоих соседей
- Либо строго больше их же
Например, на следующем рисунке зелёным выделены «дубы», которые можно удалить:

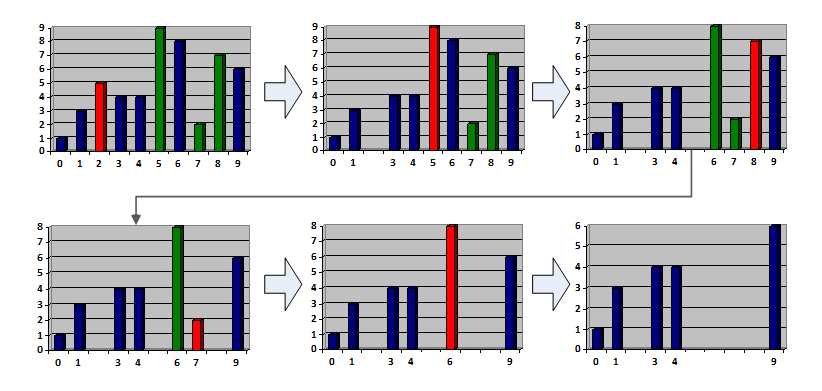
- Надо за минимальное количество операций превратить последовательность в нестрого возрастающую. Последовательность удалений также надо вывести. Например, так:

Если хотите, можете подумать (название поста может Вам подсказать).
Основная идея
Как можно было догадаться из тегов — решение есть некая динамика. Если Вы забыли или не знали, что такое динамическое программирование, я напомню. Идея динамики в том, что для совсем маленьких примеров (например, одно дерево) ответ очевиден (ничего не пилить), а для больших решение можно получить, зная решения для каких-то более мелких независимых подзадач. В этом месте динамика очень напоминает индукцию. Как же свести задачу, например, для десяти деревьев к меньшим? Предположим, что мы уже знаем ответ (мы не будем этим пользоваться, но это полезно представить). В нём есть два крайних дерева и какая-то середина. Давайте переберём любое дерево из этой середины (вообще любое, которое лежит по высоте между границами — в противном случае его оставлять нельзя):

Можно заметить, что все операции будут производиться либо в левой части, либо в правой. Значит, друг от друга они не зависят никак. Вот и разбили на две независимые подзадачи. Можно прорелаксировать (выбрать лучший) ответ на нашем большом отрезке.
А что делать, когда на отрезке между нашими границами нет деревьев (например, деревья 4 и 9)? Тут мы понимаем, что в таком случае нам нужно срубить все деревья на интервале. Вопрос — в каком порядке? Есть соблазн сделать жадный алгоритм: срубать первое попавшееся дерево и так, пока они не кончатся. Однако он неверен:

Думаю, очевидно, что не стоит придумывать различные оптимизации в стиле «на последних двух шагах запустить перебор» и пр. — это всё обламывается большим случайным тестом.
Нужно что-то поумнее. Смотрим на название поста еще разок и придумываем очень похожуюю динамику по подотрезкам: для двух деревьев и меньше удалять вообще ничего не надо. А для большего количества надо перебрать дерево, которое удалим последним и заметить, что опять получили две подзадачи: слева и справа. Единственный отличающий момент — надо проверить, что это дерево можно будет в конце удалить (когда его соседями станут границы интервала)

Например, удалить дерево 4 последним можно, а 3 — нельзя.
Восстановление ответа
Ответ восстанавливается классическим методом — запоминаем оптимальный переход из каждого состояния (где достигся самый лучший ответ) в массив, а потом идём с конца. В динамике по подотрезкам восстановление удобно писать рекурсивно:
Восстановление ответа
vector<int> ans; // Последовательность удалений
// a и b - границы интервала, на котором хотим срубить все деревья
void deleteAll(int a, int b) {
assert(del[a][b] >= 0);
if (del[a][b] == a) return;
deleteAll(a, del[a][b]);
deleteAll(del[a][b], b);
ans.push_back(del[a][b]);
}
// аналогично
void restoreAns(int a, int b) {
assert(fr[a][b] >= 0);
if (fr[a][b] == a) {
deleteAll(a, b);
return;
}
restoreAns(a, fr[a][b]);
restoreAns(fr[a][b], b);
}Время работы
Всего у нас O(n2) состояний каждой динамики (по одному на каждый подотрезок). В каждой динамике переход производится за O(n) — перебрать дерево внутри интервала. При восстановлении ответа каждое состояние мы посещаем не более одного раза. Получается квадрат, но так это асимпотически (бесконечно меньше на бесконечно больших n) меньше куба, то им можно пренебречь.
Итоговое время работы — O(n3), что при n=200 составляет O(8*106), что отрабатывает мгновенно. Это нас тоже устраивает.
Как писать
Для начала надо считать данные в массив/вектор. Это Вы делать умеете.
Первая динамика
Далее надо подсчитать динамику для удаления всех деревьев. Будем хранить её в массиве int del[a][b] — -1, если невозможно удалить все деревья на интервале (a, b), и номер последнего дерева иначе.
Для перебора подотрезков есть соблазн написать два цикла:
for (int left = 0; left < n; left++)
for (int right = left; right < n; right++) {
// ...
}Однако это в корне неверно, посколько переход динамики будет верным только тогда, когда мы знаем ответ для «меньших» подзадач. В нашем случае — для подотрезков меньшей длины. Поэтому надо сначала перебрать длину отрезка, а затем — начало (или конец):
for (int l = 2; l < n; l++)
for (int a = 0; a + l < n; a++) {
int b = a + l;
// ...
}В этом цикле надо перебрать последнее дерево и проверить возможность удаления. Также не следует забывать проинициализировать динамику для пустых интервалов:
// Можем ли мы удалить дерево высоты h2, если его соседи имеют высоты h1 и h3
bool can(int h1, int h2, int h3) {
if (h1 < h2 && h3 < h2) return true;
if (h1 > h2 && h3 > h2) return true;
return false;
}
// ...
for (int a = 0; a + 1 < n; a++)
del[a][a + 1] = a;
for (int l = 2; l < n; l++)
for (int a = 0; a + l < n; a++) {
int b = a + l;
for (int i = a + 1; i < b; i++)
if (del[a][i] >= 0 && del[i][b] >= 0 && can(h[a], h[i], h[b])) {
del[a][b] = i;
break;
}
}Вторая динамика
Вторую динамику будем хранить в двух массивах — int dyn[a][b] и int fr[a][b]. Первый — собственно, ответ для подотрезка (сколько минимум деревьев надо удалить), или бесконечность (я использую 109), если нельзя оставить неубывающую подпоследовательность. А во втором массиве мы будем хранить либо -1, если в первом записана бесконечность, либо последнее удалённое дерево.
Итак, пишем. Тут можно инициализировать всё по ходу (отдельный цикл нужен только для заполнения бесконечностями):
// Точно также перебираем отрезки
for (int l = 1; l < n; l++)
for (int a = 0; a + l < n; a++) {
int b = a + l;
if (h[a] > h[b]) continue; // Если левая граница выше правой, тут мы бессильны
if (del[a][b] >= 0) { // Если можно удалить вообще все поддеревья, давайте попробуем
dyn[a][b] = b - a - 1;
fr[a][b] = a;
}
for (int i = a + 1; i < b; i++) {
// Если наше дерево ниже левой границы, или выше правой,
// оно нам не точно подходит - оставить мы его не можем
if (h[a] > h[i] || h[i] > h[b]) continue;
// Если хоть в одном месте будет бесконечность, то в сумме
// также будет число, большее бесконечности
int cans = dyn[a][i] + dyn[i][b];
if (dyn[a][b] > cans) {
dyn[a][b] = cans;
fr[a][b] = i;
}
}
}Восстановление ответа
Оно было уже полностью написано выше — тот код полностью работает. Осталось лишь проверить, что ответ есть, вызвать функцию, и вывести результат:
int a = 0, b = n - 1;
if (fr[0][n - 1] < 0) printf("-1\n");
else {
ans = vector<int>();
restoreAns(a, b);
printf("%d\n", ans.size());
for (int i = 0; i < ans.size(); i++)
printf("%d\n", ans[i] + 1);
}Всё вместе
Всю программу можно просмотреть на pastebin. Так как она писалась на олимпиаде, в ней присутствуют некоторые сокращения для быстрого набора и отсутствуют комментарии. Впрочем, весь значимый код я привёл в статье.
Тестирование
На тему тестирования алгоритмических задач можно написать много больших статей. Но нам же хочется побыстрее, правда же? Поэтому вспоминаем, куда мы скачали тесты в начале статьи, распаковываем их куда-нибудь (задача называется oaks) и либо ручками прогоняем все 50 тестов, либо компилируем файл check.dpr (скомпилированный) и пишем скрипт на CMD:
@echo off
for %%i IN (tests\??) DO (
del oaks.in oaks.out >nul 2>&1
copy %%i oaks.in >nul 2>&1
main >nul 2>&1
if errorlevel 1 exit
check oaks.in oaks.out %%i.a
if errorlevel 1 exit
)
echo ALL IS OK!
pauseЗапускаем. Если увидели надпись ALL IS OK! и «Нажмите Any key» — ваше решение верное. Если нет — значит есть тест, на котором оно работает неверно. Не спешите смотреть этот тест — гораздо полезнее будет самостоятельно найти и исправить баг.
Заключение
Вот и всё, что я хотел рассказать. Надеюсь, Вы всё поняли и я не зря потратил Ваше время.
Спасибо за внимание, легких вам Accepted'ов.
Буду рад конструктивной критике.