Введение
В этой статье хочется представить реализацию дерева бинарного поиска для задачи, изложенной в статье [1]. В описанной там задаче используется алгоритм «sweeping line», для которой нужно бинарное дерево с возможностью перемещения не только от корня дерева к дочерним узлам и листьям, но и по листьям в отдельности, начиная от крайнего листа (левого или правого). Задача показалась достаточно простой, потому не стал долго искать уже готовые реализации и решил сделать самостоятельно. При этом поставил дополнительную задачу — задание процедуры добавления нового листа в дерево снаружи.
Немного теории
Здесь будет совсем мало теории. Основная масса информации может быть получена в Википедии [2]. Коротко говоря, предмет повествования является древовидной структурой данных, в которой каждый элемент может иметь по два дочерних. В моем случае детей будет именно двое, что является следствием поставленной в [1] задачи. Иначе узел будет листом, т.е. детей у него не будт вообще. При добавлении нового элемента в дерево производится спуск до близжайщего по значению листа. Найденный лист заменяется на дерево, состоящее из одного родителя и двух детей. Родитель получает значение, которое равно среднеарифметическому от значений нового элемента и замененного деревом листа. Дети — это наш новый элемент и замененный лист, позиции которых (слева или справа) зависят от того, у какого элемента значение меньше. Узел с меньшим значением оказывается слева. При добавлении поддерева обязательно нужно добавить/обновить ссылки между указанными тремя элементами (связи «родитель-дитя»).
Спуск, о котором было сказано выше, производится также по принципу «больше-меньше, влево-вправо». Сравнивается значение узла со значением нового элемента. Если новое значение меньше значения узла, то спускаемся влево, а иначе (>=) движемся вправо. Как это работает наглядно показано в следующем разделе.
В итоге мы получим отсортированное множество листьев и узлов, связанных друг с другом («родитель-дитя», «левый», «правый»). Далее нужно организовать переход от одного листа к другому, соседу справа или слева. С этой логикой пришлось повозиться больше всего. Описывать ее лучше на картинках (см. следующий раздел).
Логика дерева в иллюстрациях
Начнем с добавления элемента. Если дерево пусто, то новый элемент становится корнем. Иначе создаем поддерево вместо одного из узлов. На рис. 1 изображено добавление первых двух элементов.
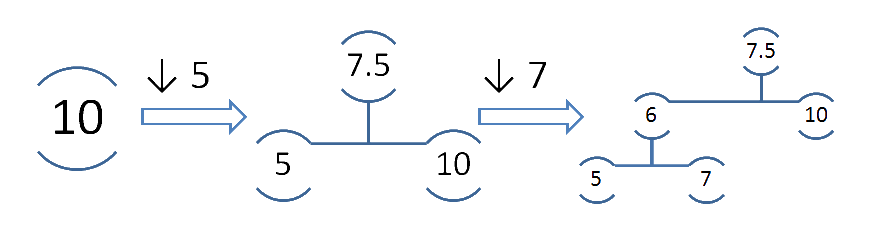
Рисунок 1. Вставка нового элемента
После того, как дерево будет заполнено, можно будет пройтись по листьям, например, слева направо. На рис. 2 изображен пример дерева. Черными стрелками обозначены переходы от одного листа к другому (соседу справа).
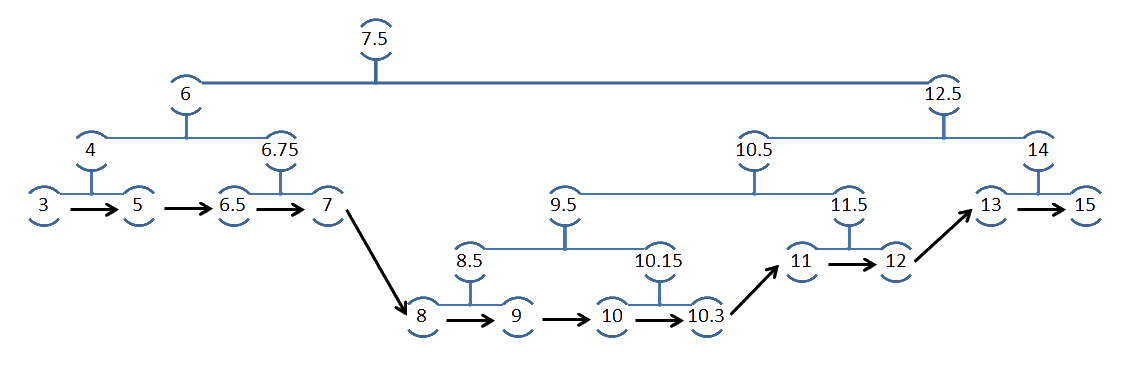
Рисунок 2. Переходы «по листьям»
Зачем нужна возможность перехода по листьям? В задаче построения диаграммы Вороного листья дерева соответствуют «аркам». Для каждой последовательности из трех арок потенциально может возникнуть «событие круга». Поэтому и нужно иметь возможность перемещаться по аркам, т.е. по листьям в дереве, как в линейном двусвязном списке. Сначала эту возможность решил реализовать только через функциональную рекуррсию. Как видно из рис. 2, самым сложным моментом при этом оказались переходы вида «7 -> 8». При использовании только рекурсии попал в вечный цикл между «7» и «6.75». Решил проблему добавлением цикла, по которому производился переход до первого родителя, не являющегося правым ребенком (в данном случае это переход от «7» к «6»). При переходе из самого правого листа («15») упомянутый цикл приведет к корню всего дерева, после чего мы получим «nil» в нотации Ruby и поиск соседей справа окончится.
Код
Класса узла "Node".
class Node
attr_accessor :val, :parent, :left, :right
def initialize( val, parent=nil, left=nil, right=nil)
@val = val
@parent, @left, @right = parent, left, right
end
def root?
return @parent.!
end
def leaf?
(@left || @right).!
end
def left?
return true unless @parent
if @parent.left
return self.equal?(@parent.left)
else
return false
end
end
def right?
return true unless @parent
if @parent.right
return self.equal?(@parent.right)
else
return false
end
end
def to_s
res = "l:"
if @left
res << "#{@left.val.to_s} s:#{@val.to_s} r:"
else
res << "nil s:#{@val.to_s} r:"
end
if @right
res << @right.val.to_s
else
res << "nil"
end
res
end
def Node.get_left_neighbour(node, up_dir = true)
return nil unless curr
if up_dir
node = curr.parent
if curr.right?
return Node.get_left_neighbour(curr.left, false) if curr.left
return Node.get_left_neighbour(node.left, false)
else
while node && node.left?
node = node.parent
end
return node ? Node.get_left_neighbour(node.parent.left, false) : nil
end
else
return curr if curr.leaf?
return Node.get_left_neighbour(curr.left, false) unless curr.right
return Node.get_left_neighbour(curr.right, false)
end
end
def Node.get_right_neighbour(curr, up_dir = true)
return nil unless curr
if up_dir
node = curr.parent
if curr.left?
return Node.get_right_neighbour(curr.right, false) if curr.right
return Node.get_right_neighbour(node.right, false)
else
while node && node.right?
node = node.parent
end
return node ? Node.get_right_neighbour(node.parent.right, false) : nil
end
else
return curr if curr.leaf?
return Node.get_right_neighbour(curr.right, false) unless curr.left
return Node.get_right_neighbour(curr.left, false)
end
end
end":val, :parent, :left, :right" — публичные свойства; соответственно, значение узла, ссылка на его родителя, а также ссылки на левого и правого потомков.
"root?, leaf?" — возвращают «true», если узел является корнем дерева или листом.
"left?, right?" — возвращают «true», если узел является левым или правым потомком.
"to_s" — возвращает строковое представление узла и его потомков.
"Node.get_left_neighbour(node, up_dir) и Node.get_right_neighbour(node, up_dir)" — возвращают левого или правого соседа для текущего узла. Т.к. функция вызывается рекуррентно, то присутствует параметр "up_dir". Значение по умолчанию «true», означает движение вверх по дереву. При вызове для листа этот параметр должен иметь значение по умолчанию.
Класс дерева "BTree".
class BTree
attr_accessor :root, :processor
def initialize(root=nil, &processor)
@root, @processor = nil, processor
end
def insert(val)
unless @root
@root = Node.new(val)
else
@processor.call(val, root)
end
self
end
def BTree.most_left(node)
return node unless node.left
return BTree.most_left(node.left)
end
def BTree.most_right(node)
return node unless node.right
return BTree.most_right(node.right)
end
def print_leafs
iterator = BTree.most_left(@root)
puts "Most left:", iterator.to_s
until iterator.!
iterator = Node.get_right_neighbour(iterator,true)
puts format("Right neigh: %s", iterator.to_s)
end
end
end":root, :processor" — публичные свойства; ссылка на корень дерева и на процедуру вставки элемента в дерево.
"insert(val)" — функция-обертка над процедурой вставки значения в бинарное дерево.
"BTree.most_left(node); BTree.most_right(node)" — статические функции, возвращающие крайние листы в дереве, корнем которого является переданный в качестве параметра узел.
"print_leafs" — выводит на консоль все листы слева-направо.
Использование дерева.
tree = BTree.new do |val, node|
iterator = node
until iterator.leaf?
iterator = (val < iterator.val) ? iterator.left : iterator.right
end
if val < iterator.val
iterator.left = Node.new(val)
iterator.right = Node.new(iterator.val)
else
iterator.right = Node.new(val)
iterator.left = Node.new(iterator.val)
end
iterator.val = (val + iterator.val)/2.0
iterator.left.parent, iterator.right.parent = iterator, iterator
puts iterator.to_s
end
tree.insert(10).insert(1).insert(8).insert(7).insert(7.5).insert(5).insert(3).insert(15).insert(12).insert(11)
tree.print_leafsВ последнем блоке кода создается дерево и процедура, осуществляющая вставку нового значения в дерево. В последних двух строках производится последовательная вставка значений в дерево и распечатка листьев. Вроде все просто.
Заключение
Код, конечно, сырой, но работает. Создавал его на платформе .Net + DLR (IronRuby) для возможности в будущем сделать отрисовку дерева с использованием WPF. Думаю этот код легко можно перенести как на чистый Ruby, так и на Silverlight.
Подобных реализаций наверняка полно в сети, но в продолжение серии про диаграмму Вороного решил все-таки представить свою реализацию. К тому же логика дерева адаптирована под конкретную задачу. Для меня важно разобрать отдельные моменты алгоритма [1] на практике самостоятельно, чтобы потом не натыкаться на чужие подводные камни.
Спасибо за внимание! Ваши комментарии…
Список литературы
1. Ход «Voronoi»
2. Двоичное дерево