Аннотация
В статье рассказывается о вычислении градиента по изображению, с использованием разностных шаблонов. Предлагается очевидный и красивый способ оптимизировать последовательность: «Смаз -> Вычисление градиента». Статья является необходимой преамбулой к планируемой статье о быстрых и хитрых алгоритмах выделения контуров и углов.
Введение
Градиент — векторная величина, показывающая направление наискорейшего возрастания некоторой величины. В нашем случае «некоторая величина» — это двумерная функция яркости изображения, допустим что мы рассматриваем «псевдонепрерывное» изображение, тогда вектор градиента определяется формулой

где I – это наше изображение.
На практике, картинка дискретна и в классическом смысле производной не существует, поэтому используют ее разностные аналоги, например в простейшем случае
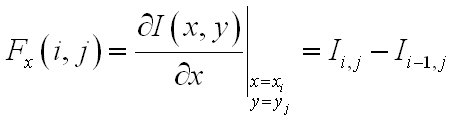
— левая разностная производная. Разностных аналогов существует великое множество, и все они обладают различными порядками аппроксимации, подробнее здесь. Увеличение порядка аппроксимации, например как тут в теории должно приводить к увеличению точности расчета производной. Более того, увеличив количество элементов в аппроксимации можно повысить устойчивость к шуму.
К примеру, будем использовать разностный аналог первой производной, шестого порядка точности аппроксимации по шагу дискретизации:

А теперь предположим, что I(i,j) — независимые случайные величины, распределенные по любому закону распределению, и посмотрим дисперсии:
- Для первой аппроксимации получаем:
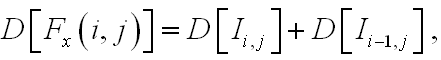
- Для второй аппроксимации получаем

Как правило дисперсию аддитивного шума можно считать изотропной и тогда вытекает соотношения
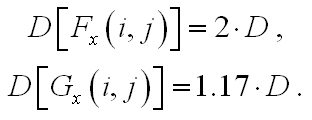
Таким образом, коэффициент усиления шума (1.17), в случае аппроксимации производной разностью более высокого порядка, меньше чем коэффициент (2) в случае аппроксимации производной левой разностью. Логично, что при этом сильно возрастают вычислительные затраты. А теперь рисуночки:
Рисунок 1 — Исходное изображение, 2 — модуль градиента по первой формуле, 3 — модуль градиента по второй формуле.

В итоге мы рассчитали градиент, на котором шумовая компонента увеличилась не в 2 раза а всего в 1.17 раз, однако опять же, если на картинке есть шум, то было бы неплохо его диспресию предварительно (до вычисления градиента) уменьшить – например, смазать исходное изображение I, то есть сделать свертку например с гауссовым ядром f. Тогда градиент запишется как:

однако, из свойств оператора свертки известна формула:
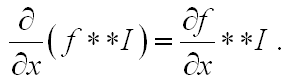
Мы вычисляем производную не по изображению, а по ядру f; и выбор точеного шаблона для расчета разностного аналога производной ограничивается лишь размерами окна.
Таким образом, можно построить алгоритм «Смаз — Вычисление градиента»:
- Вычисляем разностные аналоги производных по ядру,
- Сворачиваем полученные ядра с изображением
- В итоге, получим компоненты вектора градиента.
В вычислительном плане:
Было: Одна свертка c окном (NxN) для смаза, + две свертки со специфическими окнами (1xN, Nx1) для вычисления производных.
Стало: Две свертки со специфическими окнами (но уже NxN) для вычисления производных.
Вычисление градиента смазанного изображения задача, которая очень часто встречается, например, в хитрых детекторах углов и контуров, о которых будет следующая статья.
Что будет работать быстрее, а главное — устойчивее к шуму? Я предлагаю ответить на этот вопрос в комментариях к статье самим читателям.