Введение
Задача RMQ весьма часто встречается в спортивном и прикладном программировании. Удивительно, что на Хабре ещё никто не упомянул эту интересную тему. Попробую восполнить пробел.
Аббревиатура RMQ расшифровывается как Range Minimum (Maximum) Query – запрос минимума (максимума) на отрезке в массиве. Для определённости мы будем рассматривать операцию взятия минимума.
Пусть дан массив A[1..n]. Нам необходимо уметь отвечать на запрос вида «найти минимум на отрезке с i-ого элемента по j-ый».
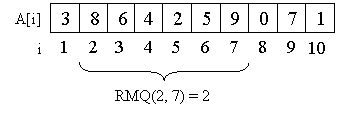
Рассмотрим в качестве примера массив A = {3, 8, 6, 4, 2, 5, 9, 0, 7, 1}.
Например, минимум на отрезке со второго элемента по седьмой равен двум, то есть RMQ(2, 7) = 2.
В голову приходит очевидное решение: ответ на каждый запрос будем находить, просто пробегаясь по всем элементам массива, лежащим на нужном нам отрезке. Такое решение, однако, не является самым эффективным. Ведь в худшем случае нам придётся пробежаться по O(n) элементам, т.е. временная сложность этого алгоритма – O(n) на один запрос. Однако, задачу можно решить эффективнее.
Постановка проблемы
Для начала уточним постановку задачи.
Что значит слово static в заголовке статьи? Задачу RMQ иногда ставят с возможностью изменения элементов массива. То есть к запросу взятия минимума добавляется возможность изменения элемента, или даже изменения элементов на отрезке (например, увеличения всех элементов на подотрезке на 3). Такой вариант задачи, называемый dynamic RMQ, я рассмотрю в последующих статьях.
Замечу здесь же, что задачу RMQ подразделяют на offline и online версии. В offline-варианте есть возможность сначала получить все запросы, проанализировать их каким-нибудь образом и только потом выдать на них ответ. В online-постановке запросы даются по очереди, т.е. следующий запрос поступает только после ответа на предыдущий. Заметим, что решив RMQ в online-постановке, мы сразу получаем решение и для offline RMQ, правда, может существовать более эффективное решение для offline RMQ, не применимое для online-постановки.
В этой статье мы будем рассматривать static online RMQ.
Время препроцессинга
Для оценки эффективности алгоритма введём ещё одну временнýю характеристику – время препроцессинга. В ней будем учитывать время на подготовку, т.е. предподсчёт некоторой информации, необходимой для ответа на запросы.
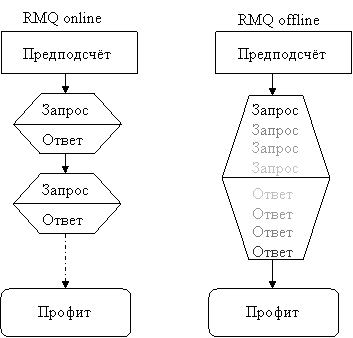
Казалось бы, зачем нам надо выделять препроцессинг отдельно? А вот зачем. Приведём ещё одно решение задачи.
Перед тем как начать отвечать на запросы, возьмём и просто насчитаем ответ для каждого отрезка! Т.е. построим массив P[n][n] (в дальнейшем я буду пользоваться C-подобным синтаксисом, хотя массив A буду нумеровать с единицы для простоты реализации), где P[i][j] будет равняться минимуму на отрезке с i до j. Причём насчитаем этот массив хоть за O(n3) – самым тупым образом, пробегаясь по всем элементам для каждого отрезка. Зачем мы это делаем? Предположим, количество запросов q намного больше n3. Тогда общее время работы нашего алгоритма – O(n3) + q * O(1) = O(q), т.е. время на препроцессинг по большому счёту и не повлияет на общее время работы алгоритма. Зато благодаря насчитанной информации мы научились отвечать на запрос за время O(1) вместо O(n). Ясно, что O(q) лучше O(qn).
С другой стороны, при q < n3 время препроцессинга будет играть свою роль, и в приведённом алгоритме оно – O(n3) – к сожалению, является слишком большим, даже несмотря на то, что его можно снизить (подумайте как) до O(n2).
Начиная с этого момента будем обозначать временные характеристики алгоритма как (P(n), Q(n)), где P(n) – время на предподсчёт и Q(n) – время на ответ на один запрос.
Итак, мы имеем два алгоритма. Один работает за (O(1), O(n)), второй – за (O(n2), O(1)). Научимся решать задачу за (O(nlogn), O(1)), где logn – двоичный логарифм n.
Лирическое отступление. Заметим, что в качестве основания логарифма можно брать любое число, т.к. logan всегда отличается от logbn ровно в константное число раз. Константа, как мы помним из курса школьной алгебры равна logab.
Итак, мы дошли до следующего шага:
Sparse Table, или разреженная таблица
Sparse Table – это таблица ST[][] такая, что ST[k][i] есть минимум на полуинтервале [A[i], A[i+2k]). Иными словами, она содержит минимумы на всех отрезках, длина которых есть степень двойки.
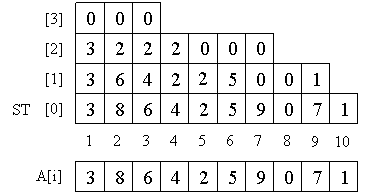
Насчитаем массив ST[k][i] следующим образом. Понятно, что ST[0] просто и есть наш массив A. Далее воспользуемся понятным свойством:
ST[k][i] = min(ST[k-1][i], ST[k-1][i + 2k — 1]). Благодаря нему мы можем сначала посчитать ST[1], потом ST[2] и т. д.
Заметим, что в нашей таблице O(nlogn) элементов, потому что номера уровней должны быть не больше logn, т. к. при больших значениях k длина полуинтервала становится больше длины всего массива и хранить соответствующие значения бессмысленно. И на каждом уровне O(n) элементов.
Снова лирическое отступление: Легко заметить, что у нас остаётся много неиспользованных элементов массива. Не стоит ли по-другому хранить таблицу дабы не тратить память впустую? Оценим количество незадействованной памяти в нашей реализации. На i-ом ряду неиспользованных элементов – 2i – 1. Значит, всего неиспользованными остаётся Σ(2i – 1) = O(2logn) = O(n), т. е. в любом случае понадобится порядка O(nlogn) – O(n) = O(nlogn) места для хранения Sparse Table. Значит, можно не беспокоиться о неиспользуемых элементах.
А теперь главный вопрос: зачем мы всё это считали? Заметим, что любой отрезок массива разбивается на два перекрывающихся подотрезка длиною в степень двойки.

Получаем простую формулу для вычисления RMQ(i, j). Если k = log(j – i + 1), то RMQ(i, j) = min(ST(i, k), ST(j – 2k + 1, k)). Тем самым, получаем алгоритм за (O(nlogn), O(1)). Ура!
…почти получаем. Как мы логарифм считать собрались за O(1)? Проще всего его тоже предподсчитать для всех значений, не превосходящих n. Понятно, что асимптотика препроцессинга от этого не изменится.
А что дальше?
А в последующих статьях мы рассмотрим множество вариаций этой задачи и сюжеты, связанные с ними, как то:
- дерево отрезков
- интервальная модификация
- двумерное дерево отрезков
- смежная задача RSQ
- дерево Фенвика
- задача LCA
- персистентная постановка задачи RMQ
- …много чего интересного…
- и самая прелесть: алгоритм Фараха-Колтона и Бендера и преобразование RMQ -> LCA -> RMQ±1, позволяющее решать задачу RMQ за (O(n), O(1))
За подробностями можно обращаться, например, в умную книжку Т. Кормена, Ч. Лейзерсона, и Р. Ривеста «Алгоритмы: построение и анализ».
В последующих темах будут появляться другие источники.
Благодарю за внимание.