В первой части нашей темы мы рассмотрели решение задачи static RMQ за (O(nlogn), O(1)). Теперь мы разберёмся со структурой данных, называемой дерево отрезков, или интервалов (в англоязычной литературе – segment tree или interval tree). С помощью неё можно решать dynamic RMQ за (O(n), O(logn)).
Введём понятие дерева отрезков. Для удобства дополним длину массива до степени двойки. В добавленные элементы массива допишем бесконечности (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится). Итак, дерево отрезков это двоичное дерево, в каждой вершине которого написано значение заданной функции на некотором отрезке. Функция в нашем случае – это минимум.
Каждому листу будет соответствовать элемент массива с номером, равным порядковому номеру листа в дереве. А каждой вершине, не являющейся листом, будет соответствовать отрезок из элементов массива соответствующих листам-потомкам этой вершины.
За кажущейся монструозностью определения скрывается вполне простое понятие – обращаем взгляд на рисунок.
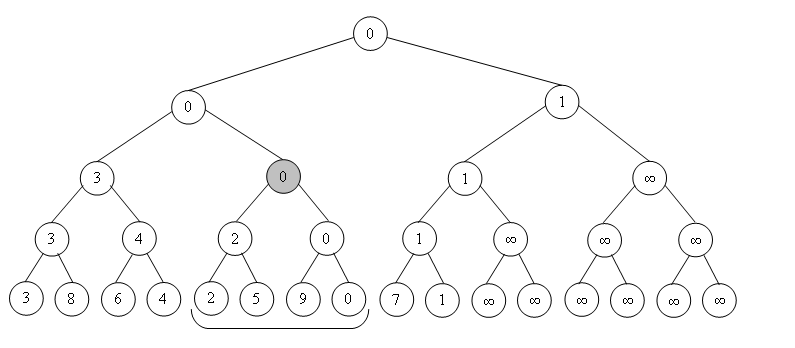
Поясним определение. Выделенной вершине будет соответствовать отмеченный отрезок, потому как он является объединением всех листов-потомков данной вершины (начиная с этого момента отождествим лист и элемент массива, который он представляет).
Хранить дерево будем подобно двоичной куче. Заведём массив T[2n – 1]. Корень будет лежать в первом элементе массива, а сыновья i-ой вершины будут лежать в элементах с номерами 2i и 2i + 1 – левый и правый соответственно. Сразу можно заметить очевидное свойство: T[i] = min(T[2i], T[2i + 1]) для i-ой вершины, не являющейся листом. Листы, к слову, будут лежать при такой нумерации в элементах с номерами от n до 2n – 1.
Построим дерево, пробежавшись по элементам с (n – 1)-ого по первый, считая минимум значений в сыновьях для каждой вершины.
Начиная с этой статьи я буду давать код для большей наглядности.
Функция build_tree(V) превращает массив V в дерево отрезков для этого массива. Итак, как теперь по отрезку найти минимум на нём? Для этого введём понятие фундаментального отрезка.
Назовём фундаментальным отрезком в массиве такой отрезок, что существует вершина в дереве, которой он соответствует. Разобьём наш отрезк на минимальное количество непересекающихся фундаментальных. Покажем, что на каждом уровне их количество не превосходит 2.
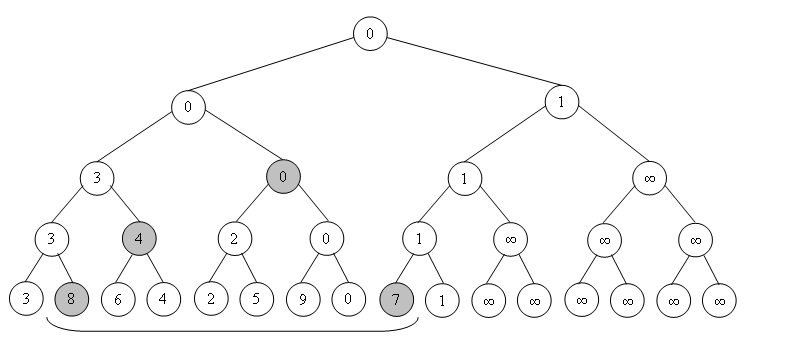
Возьмём самый большой фундаментальный отрезок в разбиении. Пусть его длина – 2t. Заметим, что фундаментальных отрезков длиной 2t – не более двух (1). Возьмём самый левый из имеющихся максимальных фундаментальных. Будем двигаться от него налево. Заметим, опять же, что длины отрезков будут убывать (2). Так же и с правым из максимальных. Тем самым получим, что фундаментальных отрезков – не более 2t, что не превосходит 2logn. Пункты (1) и (2) в доказательстве я оставлю для самостоятельного осмысления.
Чем нам это помогает? Теперь мы можем реализовать запрос минимума «снизу». Будем подниматься снизу, добавляя к ответу на каждом уровне, если надо, фундаментальный отрезок.
Заведём два указателя – l и r, с помощью которых будем находить очередные фундаментальные отрезки разбиения. Изначально установим l и r указывающими на листы, соответствующие концам отрезка запроса. Заметим, что если l указывает на вершину, являющуюся правым сыном своего родителя, то эта вершина принадлежит разбиению на фундаментальные отрезки, в противном случае не принадлежит. Аналогично с указателем r – если он указывает на вершину, являющуюся левым сыном своего родителя, то добавляем её в разбиение. После этого сдвигаем оба указателя на уровень выше и повторяем операцию. Продолжаем операции пока указатели не зайдут один за другой.
Находя очередной фундаментальный отрезок, мы сравниваем минимум на нём с текущим найденным минимумом и уменьшаем его в случае необходимости. Асимптотика работы алгоритма – O(logn), т. к. на каждом уровне мы выполняем константное число операций, а всего уровней – logn.
Теперь научимся изменять значение элемента дерева. Заметим, что для каждого листа есть ровно logn фундаментальных отрезков, которые его содержат – все они соответствуют вершинам, лежащим на пути от нашего листа до корня.
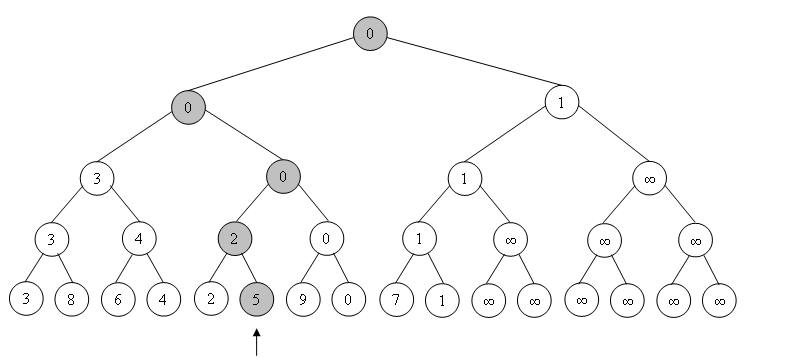
Значит, при изменении элемента достаточно просто пробежаться от его листа до корня и обновить значение во всех вершинах на пути по формуле T[i] = min(T[2i], T[2i + 1]).
Ура! Получаем решение задачи Dynamic RMQ за (O(n), O(logn)).
В следующей статье мы научимся делать запрос сверху. Несмотря на то, что асимптотика у запроса сверху будет такая же, у него есть одна большая плюшка – возможность легко и непринуждённо прикрутить модификацию на отрезке. До новых встреч!
Определение
Введём понятие дерева отрезков. Для удобства дополним длину массива до степени двойки. В добавленные элементы массива допишем бесконечности (за бесконечностью стоит понимать, например, число, больше которого в данных ничего не появится). Итак, дерево отрезков это двоичное дерево, в каждой вершине которого написано значение заданной функции на некотором отрезке. Функция в нашем случае – это минимум.
Каждому листу будет соответствовать элемент массива с номером, равным порядковому номеру листа в дереве. А каждой вершине, не являющейся листом, будет соответствовать отрезок из элементов массива соответствующих листам-потомкам этой вершины.
За кажущейся монструозностью определения скрывается вполне простое понятие – обращаем взгляд на рисунок.

Поясним определение. Выделенной вершине будет соответствовать отмеченный отрезок, потому как он является объединением всех листов-потомков данной вершины (начиная с этого момента отождествим лист и элемент массива, который он представляет).
Хранить дерево будем подобно двоичной куче. Заведём массив T[2n – 1]. Корень будет лежать в первом элементе массива, а сыновья i-ой вершины будут лежать в элементах с номерами 2i и 2i + 1 – левый и правый соответственно. Сразу можно заметить очевидное свойство: T[i] = min(T[2i], T[2i + 1]) для i-ой вершины, не являющейся листом. Листы, к слову, будут лежать при такой нумерации в элементах с номерами от n до 2n – 1.
Построение
Построим дерево, пробежавшись по элементам с (n – 1)-ого по первый, считая минимум значений в сыновьях для каждой вершины.
Начиная с этой статьи я буду давать код для большей наглядности.
const int INF = INT_MAX;
void build_tree(const vector<int>& V)
{
// размер, доведённый до степени двойки
int n = (1 << (log(n - 1) + 1));
V.resize(2 * n, INF);
// инициализируем листы
for (int i = n; i < 2 * n; i++)
V[i] = V[i - n];
// и все остальные вершины
for (int i = n - 1; i > 0; i--)
V[i] = min(V[2 * i], V[2 * i + 1]);
}
Функция build_tree(V) превращает массив V в дерево отрезков для этого массива. Итак, как теперь по отрезку найти минимум на нём? Для этого введём понятие фундаментального отрезка.
Запрос минимума
Назовём фундаментальным отрезком в массиве такой отрезок, что существует вершина в дереве, которой он соответствует. Разобьём наш отрезк на минимальное количество непересекающихся фундаментальных. Покажем, что на каждом уровне их количество не превосходит 2.

Возьмём самый большой фундаментальный отрезок в разбиении. Пусть его длина – 2t. Заметим, что фундаментальных отрезков длиной 2t – не более двух (1). Возьмём самый левый из имеющихся максимальных фундаментальных. Будем двигаться от него налево. Заметим, опять же, что длины отрезков будут убывать (2). Так же и с правым из максимальных. Тем самым получим, что фундаментальных отрезков – не более 2t, что не превосходит 2logn. Пункты (1) и (2) в доказательстве я оставлю для самостоятельного осмысления.
Чем нам это помогает? Теперь мы можем реализовать запрос минимума «снизу». Будем подниматься снизу, добавляя к ответу на каждом уровне, если надо, фундаментальный отрезок.
Заведём два указателя – l и r, с помощью которых будем находить очередные фундаментальные отрезки разбиения. Изначально установим l и r указывающими на листы, соответствующие концам отрезка запроса. Заметим, что если l указывает на вершину, являющуюся правым сыном своего родителя, то эта вершина принадлежит разбиению на фундаментальные отрезки, в противном случае не принадлежит. Аналогично с указателем r – если он указывает на вершину, являющуюся левым сыном своего родителя, то добавляем её в разбиение. После этого сдвигаем оба указателя на уровень выше и повторяем операцию. Продолжаем операции пока указатели не зайдут один за другой.
Находя очередной фундаментальный отрезок, мы сравниваем минимум на нём с текущим найденным минимумом и уменьшаем его в случае необходимости. Асимптотика работы алгоритма – O(logn), т. к. на каждом уровне мы выполняем константное число операций, а всего уровней – logn.
int rmq_up(vector<int>& T, int l, int r)
{
int ans = INF;
int n = T.size() / 2;
l += n - 1, r += n - 1;
while (l <= r)
{
// если l - правый сын своего родителя,
// учитываем его фундаментальный отрезок
if (l & 1)
ans = min(ans, T[l]);
// если r - левый сын своего родителя,
// учитываем его фундаментальный отрезок
if (!(r & 1))
ans = min(ans, T[r]);
// сдвигаем указатели на уровень выше
l = (l + 1) / 2, r = (r - 1) / 2;
}
return ans;
}
Модификация
Теперь научимся изменять значение элемента дерева. Заметим, что для каждого листа есть ровно logn фундаментальных отрезков, которые его содержат – все они соответствуют вершинам, лежащим на пути от нашего листа до корня.

Значит, при изменении элемента достаточно просто пробежаться от его листа до корня и обновить значение во всех вершинах на пути по формуле T[i] = min(T[2i], T[2i + 1]).
void update(vector<int>& T, int i, int x)
{
int n = T.size() / 2;
i += n – 1;
T[i] = x;
while (i /= 2)
T[i] = min(T[2 * i], T[2 * i + 1]);
}
Ура! Получаем решение задачи Dynamic RMQ за (O(n), O(logn)).
В следующей статье мы научимся делать запрос сверху. Несмотря на то, что асимптотика у запроса сверху будет такая же, у него есть одна большая плюшка – возможность легко и непринуждённо прикрутить модификацию на отрезке. До новых встреч!