Постановка задачи
Пусть дан массив A длины N, и дано число K ≤ N. Требуется найти максимум (минимум, сумма ...) в подотрезках длины K данного массива. Это частный случай задачи RMQ (Range Minimum Query — минимум на отрезке), но с дополнительными ограничениями — постоянная длина отрезка поиска. В данном решении задача не предполагает возможность изменения элементов массива. Для определенности будем рассматривать нахождение максимума.
Преимущества и недостатки
Данный алгоритм позволяет находить максимум на подотрезках фиксированной длины за O(1), с препроцессингом за O(N). При этом вспомогательной памяти требуется 2*N. Но основным преимуществом можно считать очень простую реализацию и понятность. Недостаток – алгоритм не адаптирован для изменения элементов исходного массива. Т.е. изменение возможно, но для этого потребуется выполнить порядка O(K) действий.
Решение
Препроцессинг
Разделим исходный массив A на блоки длиной K-1 (почему именно K-1, поймете чуть ниже). Затем рассчитаем два дополнительных массива B и C следующим образом:
в B[i] будем хранить максимум на промежутке от начала текущего блока до i-го элемента;
в C[i] будем хранить максимум на промежутке от i-го элемента до конца текущего блока.
Например в B[2] будем хранить максимум от A[0] до A[2], а в С[2] — максимум от A[2] до A[3]. Понятно, что эту операцию можно выполнить за O(n). На следующем рисунке приведен пример для N=22, K=5:
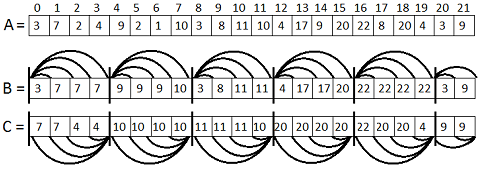
Обработка запроса
Теперь, с помощью этой нехитрой структуры, можно легко найти максимум на отрезке длины K. Мы специально сделали блоки длиной K-1, что бы края любого запроса всегда попадали в два соседних блока. И, следовательно, при любом запросе, в отрезок будет входить граница 2-х блоков. Назовем её T. Левый край отрезка — l, правый — r. Теперь для того что бы получить максимум, нам необходимо всего лишь взять max(C[l], B[r]). Действительно C[l] — это максимум на отрезке от l до T, а B[r] — максимум от T до r, и, следовательно, максимум от C[l] и B[r], будет максимумом на отрезке от l до r.
Реализация
Ниже приведена простейшая реализация на C++;
vector< int > B, C;
void
build(const vector< int > A, int k)
{
int n = A.size();
B.resize(n);
C.resize(n);
k--;
// Расчитываем B
for(int i = 0; i < n; i++)
{
if(i % k)
B[i] = max(A[i], B[i - 1]);
else
B[i] = A[i];
}
// Расчитываем C
C.back() = A.back();
for(int i = n - 2; i >= 0; i--)
{
if((i + 1) % k)
C[i] = max(A[i], C[i + 1]);
else
C[i] = A[i];
}
}
int
GetMax(int l, int k)
{
return max(C[l], B[l + k - 1]);
}
Для правильной работы так же необходимо что бы K, подаваемый на вход функций build и GetMax, был одинаковый.
Очевидно что данная реализация функции build не является оптимальной, однако она наиболее проста и понятна. На каждом следующем шаге вычисляется новое значение на основании предыдущего. Ниже приведена более скоростная реализация.
void
build(const vector< int > A, int k)
{
int n = A.size();
B.resize(n);
C.resize(n);
B.front() = A.front();
C.back() = A.back();
k--;
for(int i1(1), i2(n - 2); i1 < n; i1++, i2--)
{
B[i1] = (i1 % k) ? max(A[i1], B[i1 - 1]) : A[i1];
C[i2] = ((i2 + 1) % k) ? max(A[i2], C[i2 + 1]) : A[i2];
}
}
Итог
Как видите алгоритм очень прост и в плане реализации, и в плане понимания. Он дает асимптотически лучшую оценку O(1) для поиска максимума на подотрезке заданной длины. Эту структуру легко изменить для поиска минимума или суммы. Кроме того максимальное количество возможных вариантов будет равно N-K, и значит, с помощью этой структуры можно посчитать все возможные комбинации за O(n). В каждый момент времени, в памяти нужно хранить только два соседних блока длиной K, что уменьшит размер памяти в более продвинутых реализациях.
Авторство алгоритма принадлежит Ван Херку.
Ссылки
Задача RMQ — 1. Static RMQ
Задача RMQ — 2. Дерево отрезков
Решение этой же задачи через модификацию стека (e-maxx)
Еще немного о RMQ (e-maxx)
Большое количество информации (на английском)