Иногда полезно представить граф в графической форме, так чтобы была видна структура. Можно привести десятки примеров, где это может пригодиться: визуализация иерархии классов и пакетов исходного кода какой-нибудь программы, визуализация социального графа (тот же Twitter или Facebook) или графа цитирования (какие публикации на кого ссылаются) и т.д. Но вот незадача: количество ребер в графе зачастую настолько велико, что нарисованный граф просто невозможно разобрать. Взгляните на эту картинку:

Это граф зависимостей некой программной системы. Он представляет собой дерево разбиения на пакеты (серые шарики — пакеты, белые — классы), на которое поверх наложены ребра зависимости одних классов от других. Чтобы не рисовать стрелки направления, ребра нарисованы в виде градиентных линий, где зеленый — это начало, а красный — конец ребра. Как видите, граф настолько визуально перегружен, что архитектуру программы невозможно проследить.
Под катом описание метода, решающего эту проблему.
Идея метода гениально проста — почему бы не использовать тот же принцип, что и в кабельных сетях? Многие из нас знают, какой бардак начинается, когда проводов становится слишком много. Для того, чтобы это бардак предотвратить, провода объединяют в жгуты.
Как эту идею применить к графам и реализовать алгоритмически?
Рассмотрим пример рисования одного ребра на примере. Необходимо провести ребро из вершины P0 в вершину P4:
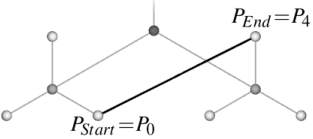
Найдем путь между этими вершинами:

Теперь проведем кривую через полигон, образованный точками P0, P1, P2, P3, P4:
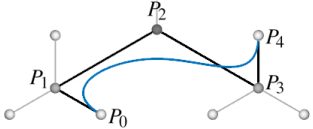
Собственно, а как это сделать? Авторы этого метода проанализировали, что лучше всего для целей визуализации в качестве кривых подходят кусочно-заданные кубические B-сплайны. Задача нахождения таких B-сплайнов является классической и давным давно решена другими. Вкратце лишь скажу, что кубический B-сплайн — это просто набор кривых третьего порядка в двухмерном пространстве, для которых выполняется условия сшивки первых и вторых производных на краях. Если кому-то захочется реализовать этот метод, не изобретайте велосипед — в конце я выложил работающий код отрисовки ребер на C#.
Для того, чтобы управлять степенью связанности ребер, вводится параметр β, который принимает значения от 0 до 1 (0 — ребра не связаны в жгут и представляют собой независимые прямые линии, 1 — ребра максимально связаны друг с другом). Математически это выглядит так:

S(t) — это точки сплайна, S'(t) — это результирующая кривая, которая и отрисовывается на экран в виде ребра.
Ну и вот результат того, во что вся эта математика выливается:

Здесь β = 0.85. Теперь архитектрура программы представляется значительно яснее. Видны отдельные связки ребер, проглядываются зависимости между пакетами.
Тот же граф, только используется радиальный способ визуализации архитектуры (без применения метода, эквивалентно β = 0):

С применением метода (β = 0.85):

Как видно, метод связывания ребер можно сочитать с различными методами рисования деревьев: в этом его большое преимущество.
Граф цитирования публикаций. Зеленый круг — это публикации 2008 года, которые ссылаются на публикации предыдущих годов (2007, 2006 и т.д.). Отмечаются только ссылки публикаций 2008 года. Без применения метода это выглядит так:

С применением метода (β = 0.99):

1. Чтобы не было вот такого:

можно использовать альфа-канал:

2. Если из контрольного полигона удалить вершину LCA (least common ancestor, наименьший общий предок между соединяемыми вершинами), то граф будет выглядеть значительно лучше. Взгляните на разницу:


Во втором случае вершина LCA исключается из набора вершин, и граф выглядит намного красивее.
Ниже выложена реализация класса-расширения System.Drawing.Graphics, который умеет рисовать кубический Б-сплайн через набор вершин.
Описанный метод связывания ребер и почти все картинки взяты из статьи «Hierarchical Edge Bundles:
Visualization of Adjacency Relations in Hierarchical Data». Автор — Danny Holten.

Это граф зависимостей некой программной системы. Он представляет собой дерево разбиения на пакеты (серые шарики — пакеты, белые — классы), на которое поверх наложены ребра зависимости одних классов от других. Чтобы не рисовать стрелки направления, ребра нарисованы в виде градиентных линий, где зеленый — это начало, а красный — конец ребра. Как видите, граф настолько визуально перегружен, что архитектуру программы невозможно проследить.
Под катом описание метода, решающего эту проблему.
Описание метода
Идея метода гениально проста — почему бы не использовать тот же принцип, что и в кабельных сетях? Многие из нас знают, какой бардак начинается, когда проводов становится слишком много. Для того, чтобы это бардак предотвратить, провода объединяют в жгуты.
Как эту идею применить к графам и реализовать алгоритмически?
Рассмотрим пример рисования одного ребра на примере. Необходимо провести ребро из вершины P0 в вершину P4:

Найдем путь между этими вершинами:

Теперь проведем кривую через полигон, образованный точками P0, P1, P2, P3, P4:

Собственно, а как это сделать? Авторы этого метода проанализировали, что лучше всего для целей визуализации в качестве кривых подходят кусочно-заданные кубические B-сплайны. Задача нахождения таких B-сплайнов является классической и давным давно решена другими. Вкратце лишь скажу, что кубический B-сплайн — это просто набор кривых третьего порядка в двухмерном пространстве, для которых выполняется условия сшивки первых и вторых производных на краях. Если кому-то захочется реализовать этот метод, не изобретайте велосипед — в конце я выложил работающий код отрисовки ребер на C#.
Для того, чтобы управлять степенью связанности ребер, вводится параметр β, который принимает значения от 0 до 1 (0 — ребра не связаны в жгут и представляют собой независимые прямые линии, 1 — ребра максимально связаны друг с другом). Математически это выглядит так:

S(t) — это точки сплайна, S'(t) — это результирующая кривая, которая и отрисовывается на экран в виде ребра.
Ну и вот результат того, во что вся эта математика выливается:

Здесь β = 0.85. Теперь архитектрура программы представляется значительно яснее. Видны отдельные связки ребер, проглядываются зависимости между пакетами.
Тот же граф, только используется радиальный способ визуализации архитектуры (без применения метода, эквивалентно β = 0):

С применением метода (β = 0.85):

Как видно, метод связывания ребер можно сочитать с различными методами рисования деревьев: в этом его большое преимущество.
Другие примеры
Граф цитирования публикаций. Зеленый круг — это публикации 2008 года, которые ссылаются на публикации предыдущих годов (2007, 2006 и т.д.). Отмечаются только ссылки публикаций 2008 года. Без применения метода это выглядит так:

С применением метода (β = 0.99):

Замечания
1. Чтобы не было вот такого:

можно использовать альфа-канал:

2. Если из контрольного полигона удалить вершину LCA (least common ancestor, наименьший общий предок между соединяемыми вершинами), то граф будет выглядеть значительно лучше. Взгляните на разницу:


Во втором случае вершина LCA исключается из набора вершин, и граф выглядит намного красивее.
Реализация на C#
Ниже выложена реализация класса-расширения System.Drawing.Graphics, который умеет рисовать кубический Б-сплайн через набор вершин.
using System;
using System.Text;
using System.Drawing;
static class GraphicsExtension
{
private static void DrawCubicCurve(this Graphics graphics, Pen pen, float beta, float step, PointF start, PointF end, float a3, float a2, float a1, float a0, float b3, float b2, float b1, float b0)
{
float xPrev, yPrev;
float xNext, yNext;
bool stop = false;
xPrev = beta * a0 + (1 - beta) * start.X;
yPrev = beta * b0 + (1 - beta) * start.Y;
for (float t = step; ; t += step)
{
if (stop)
break;
if (t >= 1)
{
stop = true;
t = 1;
}
xNext = beta * (a3 * t * t * t + a2 * t * t + a1 * t + a0) + (1 - beta) * (start.X + (end.X - start.X) * t);
yNext = beta * (b3 * t * t * t + b2 * t * t + b1 * t + b0) + (1 - beta) * (start.Y + (end.Y - start.Y) * t);
graphics.DrawLine(pen, xPrev, yPrev, xNext, yNext);
xPrev = xNext;
yPrev = yNext;
}
}
/// <summary>
/// Draws a B-spline curve through a specified array of Point structures.
/// </summary>
/// <param name="pen">Pen for line drawing.</param>
/// <param name="points">Array of control points that define the spline.</param>
/// <param name="beta">Bundling strength, 0 <= beta <= 1.</param>
/// <param name="step">Step of drawing curve, defines the quality of drawing, 0 < step <= 1</param>
internal static void DrawBSpline(this Graphics graphics, Pen pen, PointF[] points, float beta, float step)
{
if (points == null)
throw new ArgumentNullException("The point array must not be null.");
if (beta < 0 || beta > 1)
throw new ArgumentException("The bundling strength must be >= 0 and <= 1.");
if (step <= 0 || step > 1)
throw new ArgumentException("The step must be > 0 and <= 1.");
if (points.Length <= 1)
return;
if (points.Length == 2)
{
graphics.DrawLine(pen, points[0], points[1]);
return;
}
float a3, a2, a1, a0, b3, b2, b1, b0;
float deltaX = (points[points.Length - 1].X - points[0].X) / (points.Length - 1);
float deltaY = (points[points.Length - 1].Y - points[0].Y) / (points.Length - 1);
PointF start, end;
{
a0 = points[0].X;
b0 = points[0].Y;
a1 = points[1].X - points[0].X;
b1 = points[1].Y - points[0].Y;
a2 = 0;
b2 = 0;
a3 = (points[0].X - 2 * points[1].X + points[2].X) / 6;
b3 = (points[0].Y - 2 * points[1].Y + points[2].Y) / 6;
start = points[0];
end = new PointF
(
points[0].X + deltaX,
points[0].Y + deltaY
);
graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}
for (int i = 1; i < points.Length - 2; i++)
{
a0 = (points[i - 1].X + 4 * points[i].X + points[i + 1].X) / 6;
b0 = (points[i - 1].Y + 4 * points[i].Y + points[i + 1].Y) / 6;
a1 = (points[i + 1].X - points[i - 1].X) / 2;
b1 = (points[i + 1].Y - points[i - 1].Y) / 2;
a2 = (points[i - 1].X - 2 * points[i].X + points[i + 1].X) / 2;
b2 = (points[i - 1].Y - 2 * points[i].Y + points[i + 1].Y) / 2;
a3 = (-points[i - 1].X + 3 * points[i].X - 3 * points[i + 1].X + points[i + 2].X) / 6;
b3 = (-points[i - 1].Y + 3 * points[i].Y - 3 * points[i + 1].Y + points[i + 2].Y) / 6;
start = new PointF
(
points[0].X + deltaX * i,
points[0].Y + deltaY * i
);
end = new PointF
(
points[0].X + deltaX * (i + 1),
points[0].Y + deltaY * (i + 1)
);
graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}
{
a0 = points[points.Length - 1].X;
b0 = points[points.Length - 1].Y;
a1 = points[points.Length - 2].X - points[points.Length - 1].X;
b1 = points[points.Length - 2].Y - points[points.Length - 1].Y;
a2 = 0;
b2 = 0;
a3 = (points[points.Length - 1].X - 2 * points[points.Length - 2].X + points[points.Length - 3].X) / 6;
b3 = (points[points.Length - 1].Y - 2 * points[points.Length - 2].Y + points[points.Length - 3].Y) / 6;
start = points[points.Length - 1];
end = new PointF
(
points[0].X + deltaX * (points.Length - 2),
points[0].Y + deltaY * (points.Length - 2)
);
graphics.DrawCubicCurve(pen, beta, step, start, end, a3, a2, a1, a0, b3, b2, b1, b0);
}
}
}
* This source code was highlighted with Source Code Highlighter.Литература
Описанный метод связывания ребер и почти все картинки взяты из статьи «Hierarchical Edge Bundles:
Visualization of Adjacency Relations in Hierarchical Data». Автор — Danny Holten.