Аннотация
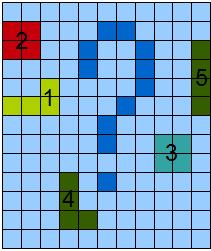 Раз, два, три, четыре, пять. Будем в прятки мы играть. В статье рассказывается про алгоритм разметки (или подсчета) объектов на бинарном изображении и о том, как без дополнительного прохода вычисляются (в еще неопубликованной части 2) геометрические характеристики этих объектов. Алгоритмы подобного типа часто используются при распознавании образов на бинарном препарате и показывают свою вычислительную эффективность.
Раз, два, три, четыре, пять. Будем в прятки мы играть. В статье рассказывается про алгоритм разметки (или подсчета) объектов на бинарном изображении и о том, как без дополнительного прохода вычисляются (в еще неопубликованной части 2) геометрические характеристики этих объектов. Алгоритмы подобного типа часто используются при распознавании образов на бинарном препарате и показывают свою вычислительную эффективность.В завершении статьи, читателям предлагается интересная задачка, грамотное решение которой существует и необходимо, при практической реализации алгоритма. Приводится исходный код, но в отличии от предыдущих моих постов, он выполнен не на языке MatLab а в абсолютно свободной, не менее мощной среде SciLab.
Введение
В практических приложениях, рассчитанных на использование в реальном времени распознавание образов часто выполняют в виде следующей последовательности:
Получение изображения (1) -> Адаптивная бинаризация (2) -> Серия морфологических операций (3) -> Разметка объектов (4) -> Заполнение пространства признаков объектов (5).
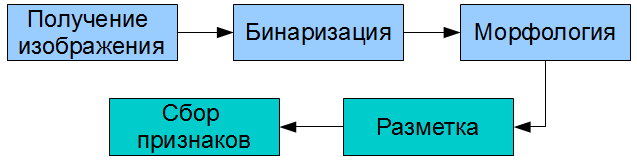
Рисунок 1 — Упрощенная схема распознавания образов на изображении. Схема исключает этапы разделения пространства признаков и принятия решения.
На рисунке 2 изображены фрагменты изображения после бинаризации и серии морфологических операций (рис.2а) и собственно результат разметки (рис.2б).
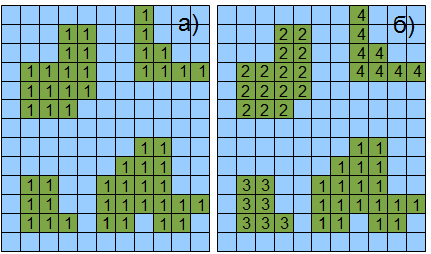
Рисунок 2 — а) — бинаризованное изображение, б) — изображение с размеченными объектами.
В статье мы будем не только размечать объекты, но подсчитывать геометрические характеристики такие как площадь и периметр. Их соотношения могут описывать компактность объекта и фактор формы Малиновского, а в комбинации с более сложными геометрическими признаками — вытянутость и особенности контура.
По научному, то что мы хотим получить, называется — выделение связных областей. Существует множество решений данной задачи — основанные на шаблонах [1], некоторые рекурсивные реализации (например листинг 1 из [2]) и др.
void Labeling(BIT* img[], int* labels[])
{
int L = 1;
for(int y = 0; y < H; ++y)
for(int x = 0; x < W; ++x)
Fill(img, labels, x, y, L++);
}
void Fill(BIT* img[], int* labels[], int x, int y, int L)
{
if( (labels[x][y] == 0) & (img[x][y] == 1) )
{
labels[x][y] = L;
if( x > 0 )
Fill(img, labels, x – 1, y, L);
if( x < W — 1 )
Fill(img, labels, x + 1, y, L);
if( y > 0 )
Fill(img, labels, x, y — 1, L);
if( y < H — 1 )
Fill(img, labels, x, y + 1, L);
}
}
* This source code was highlighted with Source Code Highlighter.
Листинг 1 — рекурсивная реализация алгоритма разметки связных областей.
Это все нам не подходит.
Область пикселей будем называть связной, если для каждого пикселя из этой области существует сосед из этой же области. Про виды связности я приводил иллюстрацию в этом топике(Рис.1,2). Наш алгоритм будет четырех связным, хотя его без особых умственных усилий можно переделать и для восьми связного варианта.
Однопроходный, не рекурсивный алгоритм разметки
Идея данного алгоритма основана на использовании уголка — ABC-маски, которая показана на рисунке 3.

Рисунок 3 — ABC маска и направление последовательного сканирования изображения.
Проход по изображению данной маской осуществляется слева-направо и сверху-вниз. Считается, что за границей изображения объектов нет, поэтому, если туда попадают B или C — это требует дополнительной проверки при сканировании. На рисунке 4 изображены 5 возможных позиций маски на изображении.
Рассмотрим их.
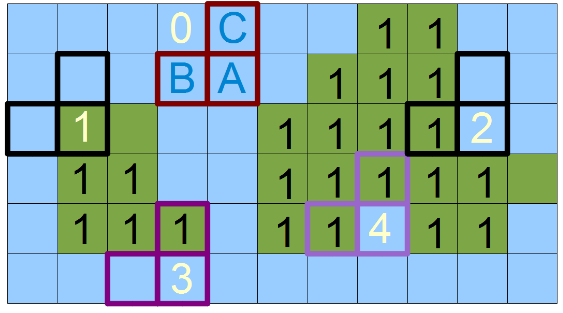
Рисунок 4 — Пять возможных позиций ABC-маски
- Позиция под номером 0, когда не размечены все три компонента маски — в этом случае мы просто пропускаем пиксель.
- Позиция под номером 1, когда помечен только элемент A — в этом случае мы говорим о создании нового объекта — новый номер.
- Позиция под номером 2, когда помечен элемент элемент B — в этом случае мы помечаем текущий пиксель A меткой, расположенной в B.
- Позиция под номером 3, когда помечен элемент элемент С — в этом случае мы помечаем текущий пиксель A меткой, расположенной в С.
- Позиция под номером 4, тогда мы говорим о том, что метки (номера объектов) B и C связаны — то есть эквивалентны и пиксель A может быть помечен либо как B либо как C. В некоторых реализация составляют граф эквивалентности таких меток, с последующим его разбором, однако на мой взгляд в это нет необходимости. Мы будем делать так — в том случае, если B не равно C то перенумеруем все уже обработанные пиксели помеченные как С в метку B. Но об этом в самом конце.
Ближе к реализации.
В начале создадим тестовые данные аналогичные изображенным на рисунке 2, а именно матрицу Image состоящую из нулей и единичек.
Image = [0 0 0 0 0 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 0 0 0;
0 0 0 1 1 0 0 1 1 0 0;
0 1 1 1 1 0 0 1 1 1 1;
0 1 1 1 1 0 0 0 0 0 0;
0 1 1 1 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 0 1 1 0 0;
0 0 0 0 0 0 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 0 0;
0 1 1 0 0 1 1 1 1 1 1;
0 1 1 1 0 1 1 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0]
Matplot(Image*255) // Посмотрим на нашу матрицу как на картинке
[m,n]=size(Image); // Узнаем горизонтальный и вертикальные размеры матрицы
km = 0; kn = 0; // Они нам еще пригодятся
cur = 1; // Переменная для подсчета объектов
* This source code was highlighted with Source Code Highlighter.
Листинг 2 — инициализация исходных данных.
А затем пройдемся по изображению выполняя серию простых и очевидных проверок. ABC-маска, которой мы проходим по картинке, проиллюстрирована на рисунке 3. Возможные комбинации, которые проверяются этой маской изображены на рисунке 4.
// Цикл по пикселям изображения
for i = 1:1:m
for j = 1:1:n
kn = j — 1;
if kn <= 0 then
kn = 1;
B = 0;
else
B = Image(i,kn); // Смотри рисунок 3 в статье
end
km = i — 1;
if km <= 0 then
km = 1;
C = 0;
else
C = Image(km,j); // Смотри рисунок 3 в статье
end
A = Image(i,j); // Смотри рисунок 3 в статье
if A == 0 then // Если в текущем пикселе пусто — то ничего не делаем
elseif B == 0 & C == 0 then // Если вокруг нашего пикселя пусто а он не пуст — то это повод подумать о новом объекте
cur = cur + 1;
Image(i,j) = cur;
elseif B ~=0 & C == 0 then
Image(i,j) = B;
elseif B == 0 & C ~= 0 then
Image(i,j) = C;
elseif B ~= 0 & C ~= 0 then
if B == C then
Image(i,j) = B;
else
Image(i,j) = B;
Image(Image == C) = B;
end
end
end
end
* This source code was highlighted with Source Code Highlighter.
Листинг 3 — последовательное сканирование пикселей изображения и разметка связных областей.
Результатом выполнения этого скрипта будет размеченная матрица:
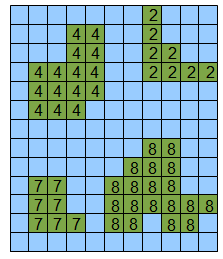
Рисунок 5 — Результат выполнения листингов 2 и 3 — объектам присвоены уникальные номера.
Недостаток — номера не последовательны, однако это по большому счету абсолютно не нужно, но исправляется дополнительными модификациями алгоритма.
В заключение первой части статьи — перенумерацию меток можно вообще не делать, если умным образом использовать матрицу указателей на специальную структуру. Над этим я предлагаю поразмыслить читателю. На языке SciLab не получится реализовать версию с указателями, однако в последней третьей части статьи я это сделаю с использованием псевдокода.
Что будет во второй части — в ней будет рассказано об эмпирических факторах форм объектов, компактности и факторе Малиновского. Мы посмотрим уникальную иллюстрацию, над которой я сейчас работаю, на которой плавное изменение формы объекта отражается возрастанием или падением его фактора-формы.
Спасибо всем прочитавшим, жду ваших отзывов.
Ссылки и использованные источники
[1] Алгоритмы / Подсчёт объектов на изображении ссылка (видимо эта статья когда-то была на Хабре, но найти не удалось)
[2] Лекция: Анализ информации содержащейся в изображении ссылка на ppt файл