Многие хабрапользователи наверняка знакомы с квайнами — программами, выводящими собственный исходный код. Сегодня я хочу показать как сделать интересный вариант квайна — ZIP-архив, который распаковывается сам в себя.
Алгоритм, используемый в ZIP-файлах (Lempel-Ziv) на самом деле довольно прост. В нём есть два вида инструкций:
Соответственно, наша задача такова: используя этот алгоритм написать программу, которая выводит свой код при запуске. Другими словами, написать сжатый поток данных который разворачивается сам в себя. Программа-максимум: написать поток который разворачивается сам в себя с произвольными данными в начале и конце (чтобы его можно было использовать как настоящий zip- или gzip-файл, с заголовком и другими необходимыми данными).
Давайте договоримся использовать
Простой квайн будет выглядеть так:
(Видно что содержимое столбцов «Код» и «Вывод» одинаково)
Интересная часть программы — последовательность из 6 байт
Если мы пишем квайн на Питоне, обычно проблемой является то что оператор
Операторы-пустышки
(Вывод равен коду плюс
Мне пришлось потратить большую часть воскресенья чтобы добраться до этой точки, но когда у меня получилось, я уже знал что победил. Из своих экспериментов я выяснил, что довольно легко создать программу которая выводит саму себя без нескольких инструкций или даже такую которая выводит себя с префиксом, минус несколько инструкций. Дополнительные байты
Вот так выглядит программа с произвольными префиксом и суффиксом:
(Вывод это P, потом байты из колонки «Код», потом S.)
Теперь переходим к реальным действиям. Мы разрешили основную технологическую проблему создания рекурсивного ZIP-файла, но осталось ещё несколько деталей.
Первая проблема: перевести наш квайн, записанный в упрощённых опкодах, в реальные опкоды Lempel-Ziv. RFC 1951 определяет формат DEFLATE, используемый в gzip и zip; последовательность блоков, каждый из которых содержит последовательность опкодов закодированных кодированием Хаффмана. Кодирование Хаффмана назначает строки разной длины разным опкодам, что не совпадает с нашим предположением о том что у опкодов одинаковая длина. Но постойте! Мы можем, если постараемся, найти кодирование с фиксированной длиной, которое можно будет использовать.
В DEFLATE существуют блоки литералов и блоки опкодов. Заголовок блока литералов это 5 байт:

Если наши опкоды L занимают по 5 байт каждый, опкоды R тоже должны занимать по 5 байт, и каждый байт выше будет повторён пять раз (например, аргумент для L4 теперь занимает 20 байт, и R4 повторяет последние 20 байт вывода). Блок опкодов с одним

К счастью, блок опкодов содержащий две инструкции
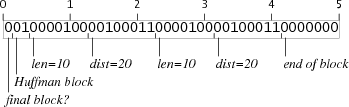
Кодирование

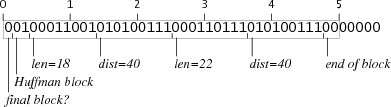
Блок, повторяющий последние 10 байт на 2 бита меньше чем нужно, но за каждым блоком повтора следует блок литералов, который начинается с трёх нулевых битов и добивки до границы ближайшего байта. Если блок повтора заканчивается за 2 бита до границы и за ним следует блок литералов, добивка вставит недостающие два бита. Точно так же блок повторяющий 40 байт выходит за границу на 5 бит, но эти биты нулевые. Начиная блок на 5 бит позже мы отнимаем эти биты у добивки. Оба этих трюка работают потому что последние 7 бит любого блока повтора — нулевые, и биты в первом байте блока литералов тоже нулевые, так что граница не видна. Если бы блок литералов начинался с одного бита, этот хитрый приём бы не сработал.
Второе препятствие состоит в том что zip-архивы (и gzip тоже) хранят контрольную сумму несжатых данных. Так как несжатые данные представляют собой тот же самый zip-архив, контрольная сумма тоже участвует в расчёте. Стало быть, нам надо найти такое значение
Команда CRC32 интерпретирует весь файл как одно большое число и вычисляет остаток при делении этого числа на определённую константу используя специальный метод деления. Мы могли бы выписать соответствующие уравнения и решить их для
Если Вы захотите повторить всё это самостоятельно, Вас ждёт ещё парочка несложных проблем, например сделать так чтобы длина tar-файла делилась без остатка на 512 и сжатие заголовка zip до 59 байт чтобы
Итак, у меня получились файлы r.gz (gzip-архив), r.tar.gz (tar-файл, сжатый gzip), и r.zip (zip-архив). Жаль, но я не смог найти программу, которая бы рекурсивно распаковывала эти файлы до бесконечности. Было бы забавно понаблюдать, но похоже намного менее сложные zip-бомбы уже испортили нам всё веселье.
Если чувствуете себя в форме, вот rgzip.go, программа на Go, генерирующая эти файлы. Интересно, получится ли у Вас создать zip-файл, содержащий gzip файл, содержащий в свою очередь оригинальный zip-файл). Кен Томпсон предложил попробовать создать zip-архив, распаковывающий свою копию но немного большего размера, чтобы при рекурсивном распакавывании размер архива рос до бесконечности (если у Вас получится то или другое, пожалуйста, оставьте комментарий).
Алгоритм Lempel-Ziv
Алгоритм, используемый в ZIP-файлах (Lempel-Ziv) на самом деле довольно прост. В нём есть два вида инструкций:
literal(n), за которым следует поток данных который надо вывести как есть, и repeat(d, n), который возращается назад на d байт и выводит n байт с этой позиции.Соответственно, наша задача такова: используя этот алгоритм написать программу, которая выводит свой код при запуске. Другими словами, написать сжатый поток данных который разворачивается сам в себя. Программа-максимум: написать поток который разворачивается сам в себя с произвольными данными в начале и конце (чтобы его можно было использовать как настоящий zip- или gzip-файл, с заголовком и другими необходимыми данными).
Давайте договоримся использовать
Ln и Rn в качестве сокращений для literal(n) и repeat(n, n), и программа предполагает что каждый код это один байт. L0, соответственно, это аналог NOP в Lempel-Ziv, L5 hello выведет hello; то же самое выведет L3 hel R1 L1 o.Простой квайн будет выглядеть так:
| Код | Вывод | |||
|---|---|---|---|---|
| no-op | L0 |
|||
| no-op | L0 |
|||
| no-op | L0 |
|||
| вывести 4 байта | L4 L0 L0 L0 L4 |
L0 L0 L0 L4 |
||
| повторить 4 последних байта | R4 |
L0 L0 L0 L4 |
||
| вывести 4 байта | L4 R4 L4 R4 L4 |
R4 L4 R4 L4 |
||
| повторить 4 последних байта | R4 |
R4 L4 R4 L4 |
||
| вывести 4 байта | L4 L0 L0 L0 L0 |
L0 L0 L0 L0 |
(Видно что содержимое столбцов «Код» и «Вывод» одинаково)
Интересная часть программы — последовательность из 6 байт
L4 R4 L4 R4 L4 R4, которая выводит 8 байт: R4 L4 R4 L4 R4 L4 R4. То есть, выводит саму себя с одним байтом до и одним после.Если мы пишем квайн на Питоне, обычно проблемой является то что оператор
print всегда длиннее того что он выводит. Мы решаем эту проблему с помощью рекурсии, подставляя строку для печати в саму себя. Здесь мы можем использовать другой подход. Программа на Lempel-Ziv частично повторяется, таким образом что повторяемая подстрока содержит весь изначальный фрагмент. Рекурсия здесь в самом представлении программы, а не в выполнении. В любом случае, этот фрагмент критически важен. До финального R4 вывод программы отстаёт от ввода. После выполнения, вывод на один байт опережает ввод.Операторы-пустышки
L0 можно использовать и в более общем варианте программы, который может дополнять себя произвольными трёхбайтовыми префиксом и суффиксом:| Код | Вывод | |||
|---|---|---|---|---|
| вывести 4 байта | L4 aa bb cc L4 |
aa bb cc L4 |
||
| повторить 4 последних байта | R4 |
aa bb cc L4 |
||
| вывести 4 байта | L4 R4 L4 R4 L4 |
R4 L4 R4 L4 |
||
| повторить 4 последних байта | R4 |
R4 L4 R4 L4 |
||
| вывести 4 байта | L4 R4 xx yy zz |
R4 xx yy zz |
||
| повторить 4 последних байта | R4 |
R4 xx yy zz |
(Вывод равен коду плюс
aa bb cc добавленные в начало и xx yy zz , добавленные в конец)Мне пришлось потратить большую часть воскресенья чтобы добраться до этой точки, но когда у меня получилось, я уже знал что победил. Из своих экспериментов я выяснил, что довольно легко создать программу которая выводит саму себя без нескольких инструкций или даже такую которая выводит себя с префиксом, минус несколько инструкций. Дополнительные байты
aa bb cc в выводе позволяют добавить к программе нужный фрагмент. Так же несложно написать код, который выводит себя плюс дополнительные три байта xx yy zz. Эти два приёма можно использовать чтобы добавить к архиву заголовок и дополнительные данные в конце.Вот так выглядит программа с произвольными префиксом и суффиксом:
| Код | Вывод | |||
|---|---|---|---|---|
| выводим префикс | [P] |
P |
||
| выводим p+1 байт | Lp+1 [P] Lp+1 |
[P] Lp+1 |
||
| повторяем последние p+1 байт | Rp+1 |
[P] Lp+1 |
||
| выводим 1 байт | L1 Rp+1 |
Rp+1 |
||
| выводим 1 байт | L1 L1 |
L1 |
||
| выводим 4 байта | L4 Rp+1 L1 L1 L4 |
Rp+1 L1 L1 L4 |
||
| повторяем 4 последних байта | R4 |
Rp+1 L1 L1 L4 |
||
| выводим 4 байта | L4 R4 L4 R4 L4 |
R4 L4 R4 L4 |
||
| повторяем 4 последних байта | R4 |
R4 L4 R4 L4 |
||
| выводим 4 байта | L4 R4 L0 L0 Ls+1 |
R4 L0 L0 Ls+1 |
||
| повторяем 4 последних байта | R4 |
R4 L0 L0 Ls+1 |
||
| no-op | L0 |
|||
| no-op | L0 |
|||
| выводим s+1 байт | Ls+1 Rs+1 [S] |
Rs+1 [S] |
||
| повторяем последние s+1 байт | Rs+1 |
Rs+1 [S] |
||
| выводим суффикс | [S] |
S |
(Вывод это P, потом байты из колонки «Код», потом S.)
ZIP-файл, распаковывающийся в себя
Теперь переходим к реальным действиям. Мы разрешили основную технологическую проблему создания рекурсивного ZIP-файла, но осталось ещё несколько деталей.
Первая проблема: перевести наш квайн, записанный в упрощённых опкодах, в реальные опкоды Lempel-Ziv. RFC 1951 определяет формат DEFLATE, используемый в gzip и zip; последовательность блоков, каждый из которых содержит последовательность опкодов закодированных кодированием Хаффмана. Кодирование Хаффмана назначает строки разной длины разным опкодам, что не совпадает с нашим предположением о том что у опкодов одинаковая длина. Но постойте! Мы можем, если постараемся, найти кодирование с фиксированной длиной, которое можно будет использовать.
В DEFLATE существуют блоки литералов и блоки опкодов. Заголовок блока литералов это 5 байт:

Если наши опкоды L занимают по 5 байт каждый, опкоды R тоже должны занимать по 5 байт, и каждый байт выше будет повторён пять раз (например, аргумент для L4 теперь занимает 20 байт, и R4 повторяет последние 20 байт вывода). Блок опкодов с одним
repeat(20,20) занимает несколько меньше 5 байт:
К счастью, блок опкодов содержащий две инструкции
repeat(20,10) делает то же самое и занимает ровно 5 байт:
Кодирование
repeat с другой длиной аргументов требует несколько более сложных трюков, но похоже что мы можем разработать 5-байтовые коды которые повторяют строку длиной от 9 до 64 байт. Например, вот блоки повторяющие 10 и 40 байт:

Блок, повторяющий последние 10 байт на 2 бита меньше чем нужно, но за каждым блоком повтора следует блок литералов, который начинается с трёх нулевых битов и добивки до границы ближайшего байта. Если блок повтора заканчивается за 2 бита до границы и за ним следует блок литералов, добивка вставит недостающие два бита. Точно так же блок повторяющий 40 байт выходит за границу на 5 бит, но эти биты нулевые. Начиная блок на 5 бит позже мы отнимаем эти биты у добивки. Оба этих трюка работают потому что последние 7 бит любого блока повтора — нулевые, и биты в первом байте блока литералов тоже нулевые, так что граница не видна. Если бы блок литералов начинался с одного бита, этот хитрый приём бы не сработал.
Второе препятствие состоит в том что zip-архивы (и gzip тоже) хранят контрольную сумму несжатых данных. Так как несжатые данные представляют собой тот же самый zip-архив, контрольная сумма тоже участвует в расчёте. Стало быть, нам надо найти такое значение
x, при котором контрольная сумма станет равна x. Рекурсия наносит ответный удар.Команда CRC32 интерпретирует весь файл как одно большое число и вычисляет остаток при делении этого числа на определённую константу используя специальный метод деления. Мы могли бы выписать соответствующие уравнения и решить их для
x, но мне на сегодня хватит рекурсивных загадок. Для x есть всего чуть более 4 миллиардов допустимых значений и мы вполне можем найти нужное прямым перебором.Если Вы захотите повторить всё это самостоятельно, Вас ждёт ещё парочка несложных проблем, например сделать так чтобы длина tar-файла делилась без остатка на 512 и сжатие заголовка zip до 59 байт чтобы
Rs+1 было не больше R64. Но это просто вопрос программирования.Итак, у меня получились файлы r.gz (gzip-архив), r.tar.gz (tar-файл, сжатый gzip), и r.zip (zip-архив). Жаль, но я не смог найти программу, которая бы рекурсивно распаковывала эти файлы до бесконечности. Было бы забавно понаблюдать, но похоже намного менее сложные zip-бомбы уже испортили нам всё веселье.
Если чувствуете себя в форме, вот rgzip.go, программа на Go, генерирующая эти файлы. Интересно, получится ли у Вас создать zip-файл, содержащий gzip файл, содержащий в свою очередь оригинальный zip-файл). Кен Томпсон предложил попробовать создать zip-архив, распаковывающий свою копию но немного большего размера, чтобы при рекурсивном распакавывании размер архива рос до бесконечности (если у Вас получится то или другое, пожалуйста, оставьте комментарий).