
Про генераторы случайных чисел написано очень много, но почти всегда, когда дело доходит до реализации, подразумевается (или явно говорится), что речь идет об x86/x64 и других «взрослых» архитектурах. В то же время, форумы, посвященные разработке устройств на микроконтроллерах, пестрят вопросами «как мне сгенерировать случайное число на %controllername%?». Причем диапазон ответов простирается от «смотри гугл/википедию» до «используй стандартную функцию». Далеко не всегда эта «стандартная функция» есть и устраивает разработчика по всем параметрам, чаще наоборот: то числа получаются далеки от случайных, то скорость работы слишком мала, а то полученный код вообще не помещается в свободную память.
Попробуем разобраться, какие бывают алгоритмы генерации случайных чисел, как выбрать подходящий, а главное, в чем особенности реализации этих алгоритмов на контроллерах.
Оценка «случайности»
Применения для ГСЧ могут найтись самые разные, от игрушек до серьезной криптографии. Соответственно, и требования, предъявляемые к генератору, тоже сильно варьируются. Для оценки качества (уровня «случайности») генератора существуют специальные тесты. Вот самые основные из них:
- Частотный тест. Состоит в подсчете количества нулей и единиц в последовательности битов. Единиц и нулей должно быть примерно поровну.
- Тест на последовательность одинаковых битов. Ищутся ряды одинаковых битов, вида 000...0 или 111...1. Распределение частот, с которыми встречаются ряды, в зависимости от их длины, должно соответствовать такому распределению для истинно случайного сигнала.
- Спектральный тест. К исходной последовательности применяется дискретное преобразование Фурье. Полученный спектр не должен иметь значительных пиков, которые говорили бы о наличии периодических свойств последовательности.
- Автокорреляционный тест. Подсчитывается значение корреляции между копиями последовательности, сдвинутыми друг относительно друга. Тест позволяет найти повторяющиеся участки в последовательности.
Существуют специальные наборы, включающие в себя десятки подобных тестов:
NIST — использовался в конкурсе AES для оценки алгоритмов шифрования.
DIEHARD — один из наиболее строгих существующих наборов.
Алгоритмы ГПСЧ
Любая последовательность, сгенерированная по жестко заданному алгоритму, не может считаться истинно случайной, поэтому, ведя речь об алгоритмических генераторах, употребляют термин псевдослучайная последовательность. Любой генератор псевдослучайных чисел (ГПСЧ) рано или поздно зацикливается, другое дело в том, что это «поздно» может наступить через несколько миллисекунд, а может через несколько лет. Длина цикла зависит от размера внутреннего состояния генератора N (фактически, это объем памяти, нужный генератору), и составляет от 2(N/2) до 2N бит.
Алгоритмов ГПСЧ придумано огромное множество, но далеко не все они удобны для реализации на микроконтроллерах. Мы сильно ограничены в быстродействии и доступном объеме памяти, многие контроллеры не поддерживают вещественную арифметику и даже команды умножения. Помня о подобных ограничениях, рассмотрим некоторые известные алгоритмы.
Линейный конгруэнтный метод
Очередной член последовательности рассчитывается по формуле
Xi+1 = (aXi + c) mod m
Число m определяет максимальный период последовательности, целые числа a и c — «магические» коэффициенты. Число m разумно выбирать равным степени двойки, в таком случае опреация приведения по модулю сводится к отбрасыванию старших битов. Для того, чтобы получить максимальный период, нужно соблюдать следующие условия:
— c и m должны быть взаимно простыми,
— a-1 должно быть кратно p для всех простых делителей p числа m,
— если m кратно 4 (а в нашем случае оно будет кратно), то и a-1 должно быть кратно 4.
Есть еще одна тонкость: в качестве результата следует брать только старшие биты переменной состояния X, так как для младших бит статистические параметры случайности значительно хуже. Линейный конгруэнтный алгоритм обычно реализован в качестве стандартного rand() во многих библиотеках.
Плюсы:
- максимально возможный период для заданного размера переменной состояния;
- достаточно быстрый;
- часто уже реализован в библиотеке компилятора.
Минусы:
- требуется операция умножения;
- не все биты одинаково случайны.
Резюме: быстрый и простой алгоритм для не очень ответственных применений.
Метод Фибоначчи с запаздываниями
В этом алгоритме используется соотношение
Xi = Xi-a — Xi-b,
где переменная состояния X — беззнаковое целое. Величины запаздываний a и b берутся не какие угодно, а строго определенные, для достижения максимального качества рекомендуются пары (17,5), (55,24) или (97,33). Чем больше запаздывания, тем больше период и лучше спектральные свойства последовательности. С другой стороны, для работы генератора требуется хранить max{a,b} предыдущих чисел, что не всегда приемлемо. Также для запуска генератора нужно max{a,b} чисел, которые обычно получают при помощи более простого ГПСЧ.
Плюсы:
- не требует операций умножения;
- все биты случайного числа равнозначны по статистическим свойствам.
Минусы:
- требует большого объема памяти;
- требует большого массива чисел для запуска.
Резюме: очень качественный, но ресурсоемкий алгоритм.
Регистр сдвига с линейной обратной связью
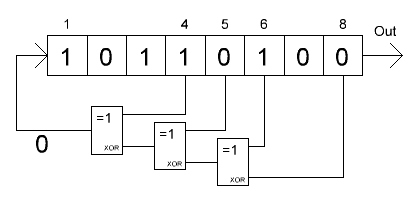
Переменная состояния хранится в регистре длины N. Генерация следующего состояния включает два шага:
- Подсчитывается значение бита C = Xi1 xor Xi2 xor… Xik, где i1, i2… ik — номера битов регистра, называемые отводами.
- Регистр сдвигается на 1 бит вправо, крайний левый бит принимает значение С.
Выходом генератора является крайний правый (или крайний левый, или любой другой) бит регистра, то есть псевдослучайная последовательность генерируется по одному биту за итерацию. При правильно выбранных номерах отводов период генератора составит 2N — 1. «Минус один», так как существует запрещенное нулевое состояние регистра. Номера отводов для N от 3 до 168 можно посмотреть в этом документе.
Кроме описанной выше конфигурации, которая, кстати, называется конфигурацией Фибоначчи (не путать с одноименным методом ГПСЧ!), существует т.н. конфигурация Галуа.

Вместо того, чтобы использовать для генерации нового крайнего левого бита сумму битов отводной последовательности, выполняется XOR каждого бита отводной последовательности с крайним правым битом, затем выполняется циклический сдвиг всего регистра вправо. Эта схема сложнее для понимания, но проще в реализации, так как все опрерации XOR можно выполнить одновременно. По длине периода и качеству псевдослучайных чисел схемы Фибоначчи и Галуа эквивалентны.
Плюсы:
- очень простая реализация, не требуется даже арифметики, только битовые операции и сдвиги;
- очень быстрый алгоритм (особенно схема Галуа);
- хорошие статистические свойства.
Минусы:
- нужно проверять начальное значение на неравенство нулю.
Резюме: очень быстрый и довольно качественный алгоритм.
Криптостойкие алгоритмы
Для применения в криптографии к ГПСЧ предъявляется еще одно существенное требование: необратимость. Все перечисленные выше алгоритмы этим свойством не обладают: зная несколько выходных значений ГПСЧ, можно, решив несложную систему уравнений, найти параметры алгоритма (те самые «магические» константы a, b, с и т.д). А зная параметры, можно воспроизвести всю псевдослучайную последовательность.
В качестве криптографически стойкого алгоритма ГПСЧ можно использовать любой достаточно сильный блочный шифр. Выбрав секретный ключ, можно получать блоки псевдослучайных чисел, применяя алгоритм к последовательным натуральным числам. Для N-битного блочного шифра период будет не больше 2N. Безопасность такой схемы полностью зависит от секретности ключа.
Все современные криптографические алгоритмы проходят проверку на использование в качестве ГПСЧ, то есть, используя сертифицированный алгоритм, не нужно специально заботиться о статистических и спектральных свойствах выходного потока. Переживать нужно только о вычислительной «прожорливости» криптоалгоритмов. Если требуется выполнять большое количество операций шифрования, имеет смысл выбрать контроллер с аппаратными криптографическими блоками. Часто в таких контроллерах есть и весьма неплохой криптостойкий аппаратный ГПСЧ.
Источники энтропии
Как уже было сказано, используя только детерминированные алгоритмы, невозможно сгенерировать истинно случайное число. Поэтому обычно применяется связка ГПСЧ + внешний источник энтропии. Источник энтропии используется для задания начального значения для ГПСЧ, а задача последнего сводится к обеспечению спектральной и статистической чистоты последовательности. Что же можно использовать в качестве источника энтропии? Да практически что угодно.
Активность пользователя
Если устройство как-либо взаимодействует с пользователем, довольно хорошим решением будет использовать в качестве источника энтропии самого пользователя. Например, время нажатия на кнопку, измеренное с точностью до микросекунды (а точнее, его младшие разряды), полностью непредсказуемо. Однако часто устройство должно работать автономно, а значит этого замечательного канала информации мы лишаемся.
Аналого-цифровой преобразователь
Во многих контроллерах есть встроенные АЦП. И во многих контроллерах они весьма посредственного качества, сделанные просто «чтобы было». Младшие биты результата АЦП почти всегда содержат значительный шум, даже если измеряется постоянное напряжение. Это можно использовать: подключите вход АЦП к напряжению питания через делитель, проведите несколько десятков измерений, возьмите младшие биты — вот вам отличное случайное число. Если АЦП содержит встроенный предусилитель, включите его, он тоже шумит.
Асинхронные генераторы
Можно использовать разницу периодов двух несинхронизированных тактовых генераторов. Большинство контроллеров содержат, например, сторожевой таймер. Для повышения надежности он тактируется от отдельного генератора, никак не связанного с основным тактовым сигналом. Достаточно подсчитать число тактов основного тактового сигнала за один период сторожевого таймера. Если подобрать периоды так, чтобы счетчик за время измерения многократно переполнился, можно получить достаточно случайное число. Недостаток этого метода — он требует много времени, до нескольких секунд.
Часы реального времени
Если в схеме есть часы реального времени, можно использовать их текущие показания для инициализации ГПСЧ. Например, преобразовав текущие дату/время в формат Unix time, мы получим сразу 32 бита, которые никогда больше не повторятся, если только не снимать показания чаще одного раза в секунду. Использование реального времени дает уникальность значений, но не дает никакой непредсказуемости, поэтому лучше комбинировать данный способ с другими.
RC-цепь
Если контроллер не имеет никаких периферийных устройств, кроме портов ввода-вывода, можно поступить следующим образом: одна из ног подсоединяется через конденсатор к земле, а через резистор — к напряжению питания. Если входы контроллера имеют внутренние подтягивающие резисторы, внешний резистор не нужен.
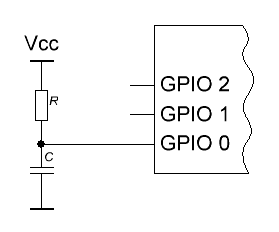
Выводим на этот порт сигнал «0» — конденсатор разряжается. Переключаем порт в режим входа — конденсатор начинает заряжаться. Когда напряжение на нем достигнет порога, вход переключится из состояния «0» в «1». Время заряда сильно зависит от многих факторов: напряжаения питания, дрейфа параметров RC-цепи, нестабильности порога, температуры, утечек, помех. Измеряя его с достаточной точностью и беря младшие биты, можно получить хорошую случайность.
Аппаратный генератор шума
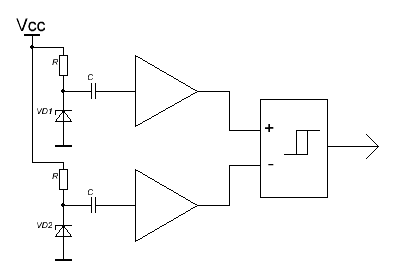
Для многих серьезных приложений (в первую очередь имеется в виду криптография), требуется более надежный источник энтропии, чем перечисленные выше. В таких случаях используют оцифровку сигнала с генератора шума, основанного на тепловом, дробовом, или даже квантовых эффектах. Шумящим элементом обычно служит специальный диод или стабилитрон, сигнал с которого усиливают и подают на компаратор, формирующий двоичный битовый поток.

Для того, чтобы порог срабатывания компаратора не влиял на статистические свойства полученного сигнала, применяют два генератора шума, работающие на один компаратор:
Заключение
Напоследок расскажу одну историю из жизни. Началась она с очередного заданного на форуме вопроса «как мне сгенерировать случайное число на контроллере?». Автор вопроса пояснил, что делает в качестве курсового проекта устройство, эмулирующее бросание игральной кости. После нескольких безуспешных попыток разобраться в алгоритмах, топикстартер поделился своим решением: он просто бросил 1000 раз настоящий кубик и забил полученными числами всю свободную память контроллера. Генератор с блеском прошел все тесты на «случайность», учитывая то, что за время демонстрации израсходовал меньше трети своего «запаса».
Следовательно, такое решение тоже имеет право на жизнь, особенно если предъявляются очень строгие требования к случайности чисел, но они требуются не слишком часто. Учитывая стремительно падающие цены на память, может быть разумным снабдить устройство флешкой с «запасом хаоса», которого хватит на все время жизни устройства.
Благодарю за внимание!
UPD1: Как было справедливо отмечено в комментариях, если предполагается атака на ГСЧ, и у злоумышленника будет аппаратный доступ к устройству, применять внешние источники энтропии нужно с большой осторожностью, так как не составляет большой сложности подменить сигнал от внешнего источника. Следует использовать внутренние источники, можно в дополнение к внешним.
Также хорошая идея — накапливать энтропию все свободное время, а использовать ее тогда, когда требуется сгенерировать очередное случайное число. Обычно в таких случаях используется т.н. Entropy pool — массив, над которым периодически выполняется одна из функций ГПСЧ, и куда постоянно подмешиваются данные из источников энтропии.
UPD2: Во многих случаях полезно содержимое Entropy pool (извините, не знаю нормального русского перевода) сохранять в EEPROM для того, чтобы после выключения-включения устройства не накапливать его заново. Это отностится, прежде всего, к получению энтропии методом асинхронных генераторов: при достаточно стабильных условиях после каждого включения может генерироваться одна и та же последовательность.
Если ожидается атака, примите меры против подмены содержимого EEPROM. Если позволяет контроллер, заблокируйте чтение/стирание/запись при помощи lock-битов, при включении контролируйте целостность EEPROM, хотя бы с помощью простейших контрольных сумм.