Странно, но статей о извлечение знаний (data mining) и кластеризации (как одном из основных инструментом, которие используются для извлечения знаний) на Хабре совсем немного. А если говорить говорить о конкретных алгоритмах, то рассматривались только hard/soft k-means.
В статье ниже описывается теория и реализация (Python + matplotlib) не очень известного, но крайне интересного иерархического метода который можно назвать алгоритмом а-квазиэквивалентности.
К сожалению, чукча не писатель (тем более не русскоязычный), поэтому тем, кто не знаком с терминами в подзаголовке, рекомендую ознакомится с Обзор алгоритмов кластеризации данных и Извлечение данных или знаний? (статьи на родном Хабре) или посмотреть в Вики (1, 2).
Будем разделятьи властвовать точки в двухмерном пространстве. Характеристиками точек будут только их координаты. Поскольку метод у нас иерархический, то результатом будет дерево\список возможных делений на кластера.
Для затравки — пример. Хотим разделить на кластера точки на изображении:
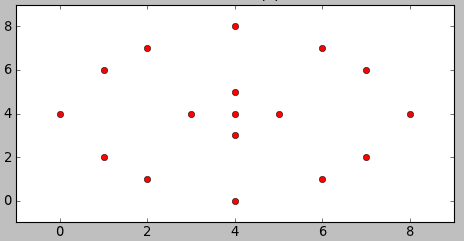
Как же должен поделить эти точки ИИ? Посмотрим, что придумает наш алгоритм.
Математика, изложенная ниже, взята из книги А. А. Барсегян, М. С. Куприянов, В. В. Степаненко, И. И. Холод — Методы и модели анализа данных OLAP и Data Mining (если быть точним — глава 7.4. Кластеризация данных при помощи нечетких отношений).
Большинство алгоритмов кластеризации (будем рассматривать k-means как эталон) для оценки схожести образцов использует расстояние между ними. Довольно логично, но думаем шире — образцы так же похожи, если похожи оценки расстояния от каждого из них ко всем остальным образцам. Что нам это даст? — Мы сможем решить и поставленную задачу, и остальные примеры, с которыми справляется k-means.
И так, как же реализованная описанная стратегия?
В конце работы алгоритма для четырех точек мы получим матрицу типа
Числа в матрице показывают, принадлежит ли пара точек отношению R, их называют уровнями квазиэквивалентности. Выбор конкретного уровня (a) разбивает множество на классы эквивалентности, которые соответствуют отделенным кластерам. То есть, если мы выберем уровень a = 0.4, то пары (1,4), (2,4), (1,3) и (2,3) уже не будут принадлежать отношению (их уровень альфа меньше, чем заданный). По сути, данную матрицу можно представлять как матрицу графа, и в случае уровня a=0.4 начальный граф разобьется на два — (1, 2) и (3, 4).
В некоторых научных работах вместе с описанием алгоритма также демонстрируют «блок-схемку»:
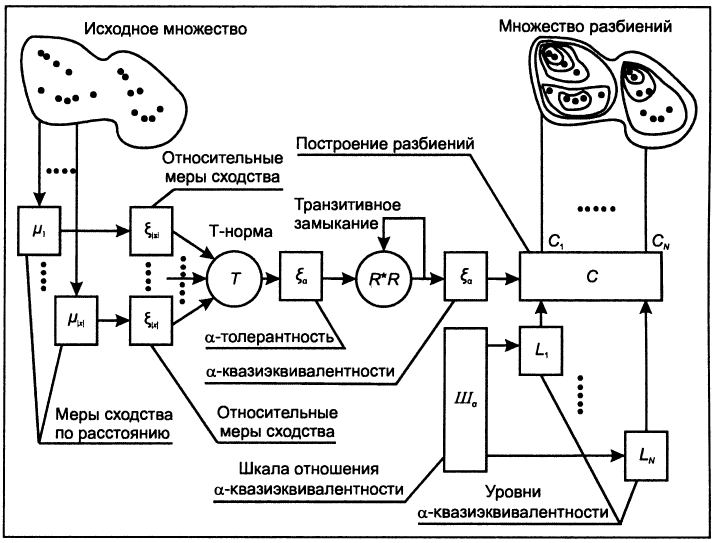
Попробуем её разобрать. С буквами «мю», «эпсилон» и Т-нормой все понятно — они есть у нас в формулах. а-толерантность и а-квазиэквивалентность — это свойства отношения, которые оно получает после применения Т-нормы и описанного замыкания. Дальше у нас разбиение на кластера, которое и вовсе можно провести эвристически (например, использовать теорию графов).
Внимательный читатель спросит — а где здесь нечеткие отношения из названия главы в книге? Именно они используются для доказательства того, что описанные шаги приведут нас к решению.
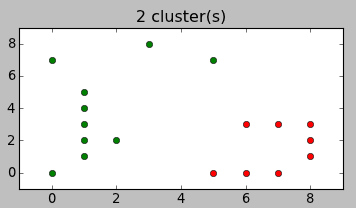
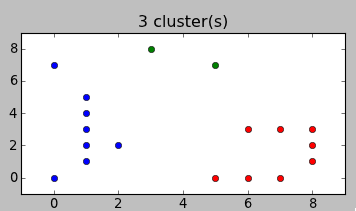
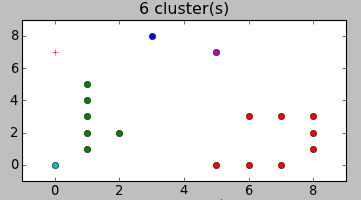
Вместо описания перевода формул в код лучше покажу, как это работает. Вот варианты разбиений, предложенные алгоритмом для примера в начале статьи:
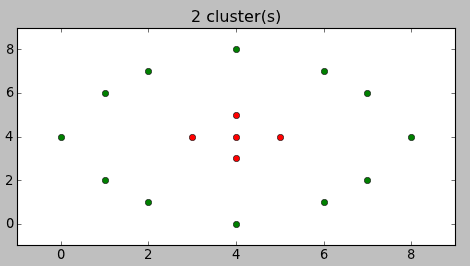
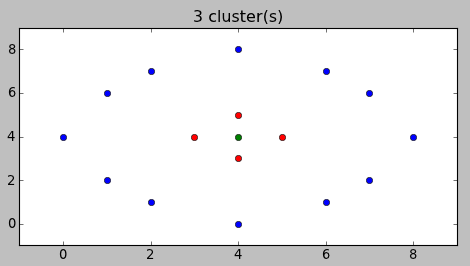
Согласитесь, довольно неожиданно, но и в тоже время — логично.
Ну и для случайных данных:
Исходный код: алгоритм, рисовалка.
Код исключительно демонстрационный и не претендует ни на эффективность, ни на соответствие PEP8.
Есть идеи использовать описанный алгоритм для решения реальной задачи анализа предложений недвижимости. Если будут интересные результаты — поделюсь.
Ссылки:
— собственно книга, теория из которой использовалась — Методы и модели анализа данных OLAP и Data Mining;
— еще одна книга по data mining от тех же авторов — Технологии анализа данных. Data Mining, Visual Mining, Text Mining, OLAP
— интереснейшая статья, в которой на похожем примере решается задача классификации — Классификация данных методом опорных векторов.
Буду признателен за замечания в личку.
В статье ниже описывается теория и реализация (Python + matplotlib) не очень известного, но крайне интересного иерархического метода который можно назвать алгоритмом а-квазиэквивалентности.
Извлечения знаний и кластеризация
К сожалению, чукча не писатель (тем более не русскоязычный), поэтому тем, кто не знаком с терминами в подзаголовке, рекомендую ознакомится с Обзор алгоритмов кластеризации данных и Извлечение данных или знаний? (статьи на родном Хабре) или посмотреть в Вики (1, 2).
Задание
Будем разделять
Для затравки — пример. Хотим разделить на кластера точки на изображении:

Как же должен поделить эти точки ИИ? Посмотрим, что придумает наш алгоритм.
Теория
Математика, изложенная ниже, взята из книги А. А. Барсегян, М. С. Куприянов, В. В. Степаненко, И. И. Холод — Методы и модели анализа данных OLAP и Data Mining (если быть точним — глава 7.4. Кластеризация данных при помощи нечетких отношений).
Большинство алгоритмов кластеризации (будем рассматривать k-means как эталон) для оценки схожести образцов использует расстояние между ними. Довольно логично, но думаем шире — образцы так же похожи, если похожи оценки расстояния от каждого из них ко всем остальным образцам. Что нам это даст? — Мы сможем решить и поставленную задачу, и остальные примеры, с которыми справляется k-means.
И так, как же реализованная описанная стратегия?
- Имеем множество X, количество элементов в множестве — Q.
Построим матрицу оценок расстояний между элементами (назовем эти оценки нормальными мерами сходства) с помощью формулы
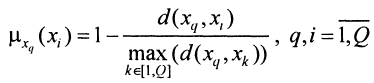
где d(x, y) — расстояние Евклида.
- Построим относительные меры сходства с помощью формулы
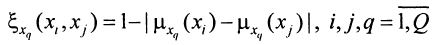
Полученная трехмерная матрица покажет, насколько похожа пара данных элементов относительно все остальных.
- Построим матрицу мер сходства элементов множества по формуле
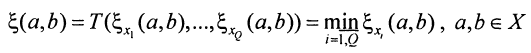
С трехмерной матрицы получили двухмерную, которая содержит худшие оценки мер сходства для каждой пары точек.
- Для полученной матрицы R построим её замыкание, используя следующие формулы:
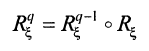
Определение для операции замыкания:
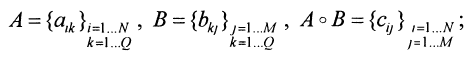
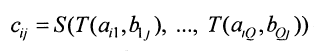
В нашем случае S = max, T = min.
В конце работы алгоритма для четырех точек мы получим матрицу типа
| 1 | 2 | 3 | 4 | |
| 1 | 1 | 0.5 | 0.3 | 0.3 |
| 2 | 0.5 | 1 | 0.3 | 0.3 |
| 3 | 0.3 | 0.3 | 1 | 0.6 |
| 4 | 0.3 | 0.3 | 0.6 | 1 |
Числа в матрице показывают, принадлежит ли пара точек отношению R, их называют уровнями квазиэквивалентности. Выбор конкретного уровня (a) разбивает множество на классы эквивалентности, которые соответствуют отделенным кластерам. То есть, если мы выберем уровень a = 0.4, то пары (1,4), (2,4), (1,3) и (2,3) уже не будут принадлежать отношению (их уровень альфа меньше, чем заданный). По сути, данную матрицу можно представлять как матрицу графа, и в случае уровня a=0.4 начальный граф разобьется на два — (1, 2) и (3, 4).
В некоторых научных работах вместе с описанием алгоритма также демонстрируют «блок-схемку»:

Попробуем её разобрать. С буквами «мю», «эпсилон» и Т-нормой все понятно — они есть у нас в формулах. а-толерантность и а-квазиэквивалентность — это свойства отношения, которые оно получает после применения Т-нормы и описанного замыкания. Дальше у нас разбиение на кластера, которое и вовсе можно провести эвристически (например, использовать теорию графов).
Внимательный читатель спросит — а где здесь нечеткие отношения из названия главы в книге? Именно они используются для доказательства того, что описанные шаги приведут нас к решению.
Практика
Вместо описания перевода формул в код лучше покажу, как это работает. Вот варианты разбиений, предложенные алгоритмом для примера в начале статьи:


Согласитесь, довольно неожиданно, но и в тоже время — логично.
Ну и для случайных данных:



Исходный код: алгоритм, рисовалка.
Код исключительно демонстрационный и не претендует ни на эффективность, ни на соответствие PEP8.
Заключение
Есть идеи использовать описанный алгоритм для решения реальной задачи анализа предложений недвижимости. Если будут интересные результаты — поделюсь.
Ссылки:
— собственно книга, теория из которой использовалась — Методы и модели анализа данных OLAP и Data Mining;
— еще одна книга по data mining от тех же авторов — Технологии анализа данных. Data Mining, Visual Mining, Text Mining, OLAP
— интереснейшая статья, в которой на похожем примере решается задача классификации — Классификация данных методом опорных векторов.
Буду признателен за замечания в личку.