В процессе реализации одной программы я столкнулся с задачей поиска простых чисел до числа N порядка 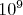 . На хабре уже неоднократно писали про различные способы и методы, но не упоминали про основной метод решения, что я сегодня и постараюсь исправить.
. На хабре уже неоднократно писали про различные способы и методы, но не упоминали про основной метод решения, что я сегодня и постараюсь исправить.
Алгоритм имеет асимптотическую сложность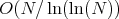 и требует
и требует  бит памяти. На входных значениях порядка
бит памяти. На входных значениях порядка 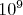 решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до
решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до 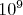 :
:
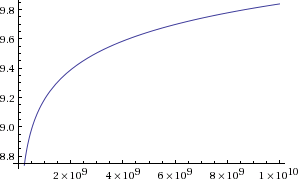
В результате можно наблюдать следующую скорость выполнения:
Для удобства и краткости создадим абстрактный класс, от которого будем наследовать реализации решета Аткина. В дальнейшем будем только создавать различные варианты класса.
Создадим базовую реализацию алгоритма:
Время исполнения базовой (классической) версии алгоритма:
Вспомним, что в языке C# операции с типом ulong занимают примерно в 3 раза больше времени, чем с типом int. В программе при расчёте больших чисел значения всё-таки переваливают за int.MaxValue, так что найдём эмпирическую планку использования. Здесь она равна 858599509. Вставим условие и получим финальное ускорение:
На этом всё. Спасибо за внимание — я постарался не быть очень сухим.
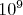 . На хабре уже неоднократно писали про различные способы и методы, но не упоминали про основной метод решения, что я сегодня и постараюсь исправить.
. На хабре уже неоднократно писали про различные способы и методы, но не упоминали про основной метод решения, что я сегодня и постараюсь исправить.Алгоритм имеет асимптотическую сложность
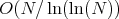 и требует
и требует  бит памяти. На входных значениях порядка
бит памяти. На входных значениях порядка 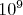 решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до
решето Аткина быстрее решета Эрастофена в 9.2 раза. Приведу график роста превосходства алгоритма Аткина на числах от 2 до 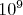 :
:
В результате можно наблюдать следующую скорость выполнения:
| 10 000 000 | 0.15 сек. |
| 100 000 000 | 2.16 сек. |
| 1 000 000 000 | 48.76 сек. |
Для удобства и краткости создадим абстрактный класс, от которого будем наследовать реализации решета Аткина. В дальнейшем будем только создавать различные варианты класса.
public abstract class AAtkin
{
internal readonly int _limit;
public bool[] IsPrimes;
protected AAtkin(int limit)
{
_limit = limit;
FindPrimes();
}
public abstract void FindPrimes();
}
Создадим базовую реализацию алгоритма:
public override void FindPrimes()
{
IsPrimes = new bool[_limit + 1];
double sqrt = Math.Sqrt(_limit);
var limit = (ulong) _limit;
for (ulong x = 1; x <= sqrt; x++)
for (ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true;
n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true;
n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true;
}
for (ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for (ulong k = s; k <= limit; k += s)
IsPrimes[k] = false;
}
IsPrimes[2] = true;
IsPrimes[3] = true;
}
Время исполнения базовой (классической) версии алгоритма:
| 1 000 000 | 0.03 сек. |
| 10 000 000 | 0.39 сек. |
| 100 000 000 | 4.6 сек. |
| 1 000 000 000 | 48.92 сек. |
Вспомним, что в языке C# операции с типом ulong занимают примерно в 3 раза больше времени, чем с типом int. В программе при расчёте больших чисел значения всё-таки переваливают за int.MaxValue, так что найдём эмпирическую планку использования. Здесь она равна 858599509. Вставим условие и получим финальное ускорение:
IsPrimes = new bool[_limit + 1];
double sqrt = Math.Sqrt(_limit);
if (sqrt < 29301)
{
for (int x = 1; x <= sqrt; x++)
for (int y = 1; y <= sqrt; y++)
{
int x2 = x * x;
int y2 = y * y;
int n = 4 * x2 + y2;
if (n <= _limit && (n % 12 == 1 || n % 12 == 5))
IsPrimes[n] ^= true;
n -= x2;
if (n <= _limit && n % 12 == 7)
IsPrimes[n] ^= true;
n -= 2 * y2;
if (x > y && n <= _limit && n % 12 == 11)
IsPrimes[n] ^= true;
}
for (int n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
int s = n * n;
for (int k = s; k <= _limit; k += s)
IsPrimes[k] = false;
}
}
else
{
var limit = (ulong) _limit;
for (ulong x = 1; x <= sqrt; x++)
for (ulong y = 1; y <= sqrt; y++)
{
ulong x2 = x*x;
ulong y2 = y*y;
ulong n = 4*x2 + y2;
if (n <= limit && (n%12 == 1 || n%12 == 5))
IsPrimes[n] ^= true;
n -= x2;
if (n <= limit && n%12 == 7)
IsPrimes[n] ^= true;
n -= 2 * y2;
if (x > y && n <= limit && n%12 == 11)
IsPrimes[n] ^= true;
}
for (ulong n = 5; n <= sqrt; n += 2)
if (IsPrimes[n])
{
ulong s = n*n;
for (ulong k = s; k <= limit; k += s)
IsPrimes[k] = false;
}
}
IsPrimes[2] = true;
IsPrimes[3] = true;
}
На этом всё. Спасибо за внимание — я постарался не быть очень сухим.