Потребовалось мне года три назад сделать классификатор текстов. В этой статье я расскажу о том как это заработало и вообще некоторые аспекты реализации и тестирования таких алгоритмов.
Классификация, согласно википедии, это одна из задач информационного поиска, заключающаяся в отнесении документа к одной из нескольких категорий на основании содержания документа.
Этим мы и будем заниматься.
Думаю, тут нет нужды расписывать зачем это нужно, ведь классификация документов давно используется в информационном поиске, в поиске плагиата, и так далее.
Для обучения классификатора (если наш классификатор обучаемый) нужна некоторая коллекция документов. Впрочем, как и для тестов.
Для этого существуют различные тестовые коллекции текстов, которые в основном можно легко найти в интернете. Я использовал коллекцию RCV1 (Reuters Corpus Volume 1). Эта коллекция отсортированных вручную новостей агентства Reuters за период с августа 1996 по август 1997 года. Коллекция содержит около 810000 новостных статей на английском языке. Она постоянно используется для разнообразных исследований в области информационного поиска и обработки текстовой информации.
Коллекция содержит иерархические категории (один документ может относится к разным категориям, например к экономике и к нефти одновременно). Каждая категория имеет свой код, и эти коды уже приписываются новостям (всего около восьмидесяти категорий). Например, во главе иерархии стоят четыре категории: CCAT (Corporate/Industrial), ECAT (Economics), GCAT (Government/Social), и MCAT (Markets).
Полный список категорий можно посмотреть здесь.
Теперь разберемся с еще несколькими важными моментами. Во-первых, для обучения классификатора неплохо бы еще сделать стемминг текстов и выбросить стоп-слова.
Подобная обработка — уже устоявшийся способ уменьшения размерности задачи и улучшения производительности.
Теперь абстрагируемся от текстовых документов и рассмотрим один из существующих алгоритмов классификации.
Не буду здесь грузить деталями и математическими выкладками. Если они интересны, то их можно найти, например, в википедии или на Хабре.
Расскажу вкратце.
Допустим, что у нас есть много точек в n-мерном пространстве, и каждая из точек принадлежит только одному из двух классов. Если мы сможем разделить их как-то на два множества гиперплоскостью размерностью n-1, то это сразу решит проблему. Так случается не всегда, но если множество линейно разделимо то нам повезло:
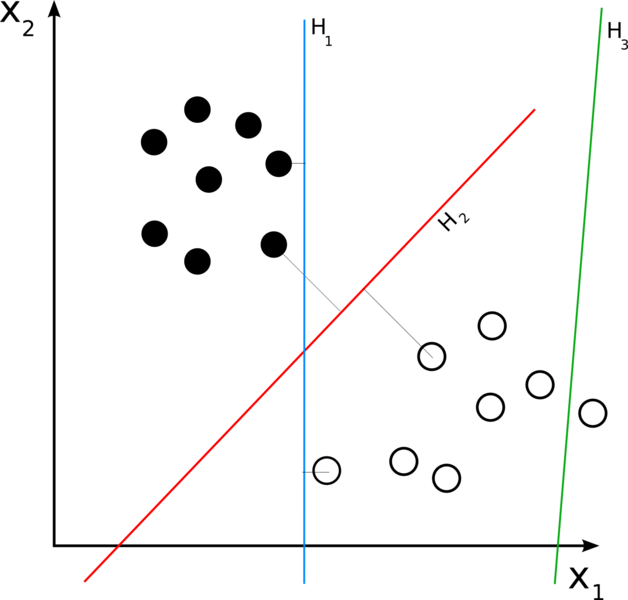
Классификатор работает тем лучше, чем больше расстояние от разделяющей гиперплоскости до ближайшей точки множества. Нам нужно найти именно такую гиперплоскость из всех возможных. Она называется оптимальной разделяющей гиперплоскостью:
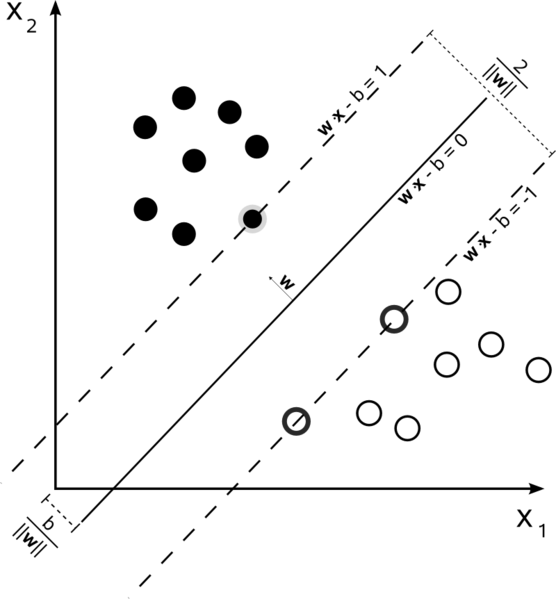
Для поиска используется простоя идея: построить две параллельные гиперплоскости, между которыми нет никаких точек множества и максимизировать расстояние между ними. Ближайшие к параллельным гиперплоскостям точки называются опорными векторами, которые и дали название методу.
А что делать, если множества не является линейно-разделимым? Тем более, что скорее всего это так. В этом случае, мы просто позволяем классификатору делить множества так, чтобы между гиперплоскостями могли оказываться точки (отсюда появляется погрешность классификатора, которую мы пытаемся минимизировать). Найдя такую гиперплоскость, классификация становится делом техники: надо посмотреть с какой стороны от гиперплоскости оказался вектор, класс которого нужно определить.
Конечно, можно реализовать алгоритм самому. Но если есть хорошие готовые решения, то это может привести к трате большого количества времени, и не факт что Ваша реализация окажется лучше или хотя бы такой же.
Есть отличная реализация support vector machine под названием SVM light. Она создана в Техническом Университете Дортмунда и распространяется бесплатно (только для исследовательских целей). Есть несколько вариантов реализации (например, умеющий обучаться на реляционных базах данных), но можно взять самый простой, работающий с текстовыми файлами. Такой классификатор состоит из двух исполняемых файлов — обучающего и классифицирующего модулей.
Обучающий модуль принимает на вход текстовый файл с обучающими данными. Файл должен содержать вектора с меткой +1 или -1 в зависимости от того, какому из двух классов он принадлежит.
Выглядит это так:
-1 0 0 0 0 0 0 6 0 0 0 6.56 0 0 0 0 0 0 0 45.56 0 0 0 0 0 0.5 0 0 0 0 0 0 0
Так же модуль поймет и такую запись:
-1 7:6 11:6.56 19:45.56 25:0.5 (то есть можно перечислить только ненулевые значения с указанием индекса).
Второй модуль принимает на вход текстовый файл с данными, которые нужно классифицировать. Формат такой же, что и для обучения. После классификации создается res.txt в котором записаны результаты.
Теперь разберемся, как можно применить svm к классификации документов. Откуда взять вектора? Как определить к каким категориям относится наш документ, если всего их 80, а svm умеет определять только принадлежность к одному из двух классов?
Представить документ в виде вектора не сложно. Сначала нужно сделать словарь коллекции — это список всех слов, которые в этой коллекции встречаются (для коллекции RCV1 это 47 000 слов). Количество слов и будет размерностью векторов. После этого документ представляется в виде вектора, где i-тый элемент это мера вхождения i-того слова словаря в документ. Это может быть + 1 или -1 в зависимости от того, входит ли слово в документ или нет, или количество вхождений. Или «доля» этого слова в документе. Вариантов много. В итоге получаются вектора большой размерности, где большая часть элементов — нули.
Если у нас 80 категорий, нам нужно запустить классификатор 80 раз. Точнее, у нас должно быть 80 классификаторов для каждой категории, умеющих определять попадает ли документ в эту категорию или нет.
Для тестирования классификатора можно использовать часть той же самой коллекции (только тогда не стоит использовать эту часть при обучении) сравнивая результаты классификатора с результатами, полученными вручную.
Для оценки работы классификаторов используются несколько метрик:
Здесь kw — количество документов, которые классификатор неправильно отметил как не относящиеся к искомой категории.
kr — количество документов, которые классификаторов правильно отметил как относящиеся к искомой категории.
r — общее количество документов, относящихся к искомой категории по мнению классификатора.
n — общее количество документов, относящихся к искомой категории.
Из этих метрик Precision и Recall являются самыми важными, так как они показывают как сильно мы ошиблись приписав документу категорию и насколько вообще наш классификатор беспорядочно работает. Чем ближе обе метрике к единице — тем лучше.
И небольшой пример. Составив вектора, взяв как меру слова в документе его «долю» (количество вхождений слова в документ деленное на общее количество слов в документе), и обучив классификатор на 32000 документов и при классификации 3000, получились следующие результаты:
Precision = 0.95
Recall = 0.75
Неплохие результаты, с ними классификатор вполне можно использовать для обработки новых данных.
Про RCV1:
О RCV1
Здесь можно найти коллекцию
Про SVM:
Википедия
Большая статья
Классификация
Классификация, согласно википедии, это одна из задач информационного поиска, заключающаяся в отнесении документа к одной из нескольких категорий на основании содержания документа.
Этим мы и будем заниматься.
Думаю, тут нет нужды расписывать зачем это нужно, ведь классификация документов давно используется в информационном поиске, в поиске плагиата, и так далее.
Коллекция
Для обучения классификатора (если наш классификатор обучаемый) нужна некоторая коллекция документов. Впрочем, как и для тестов.
Для этого существуют различные тестовые коллекции текстов, которые в основном можно легко найти в интернете. Я использовал коллекцию RCV1 (Reuters Corpus Volume 1). Эта коллекция отсортированных вручную новостей агентства Reuters за период с августа 1996 по август 1997 года. Коллекция содержит около 810000 новостных статей на английском языке. Она постоянно используется для разнообразных исследований в области информационного поиска и обработки текстовой информации.
Коллекция содержит иерархические категории (один документ может относится к разным категориям, например к экономике и к нефти одновременно). Каждая категория имеет свой код, и эти коды уже приписываются новостям (всего около восьмидесяти категорий). Например, во главе иерархии стоят четыре категории: CCAT (Corporate/Industrial), ECAT (Economics), GCAT (Government/Social), и MCAT (Markets).
Полный список категорий можно посмотреть здесь.
Теперь разберемся с еще несколькими важными моментами. Во-первых, для обучения классификатора неплохо бы еще сделать стемминг текстов и выбросить стоп-слова.
- Стемминг. Нам при классификации не важно, как написано слово «нефть» («нефть», «нефти», «нефтяной», «нефтяные») — мы всё равно поймем что это о нефти. Приведение слов к одному виду и называется стеммингом. Для стемминга текстов на английском языке есть готовые решения, например вот эта реализация алгоритма Портера. Эта библиотека написана на java в Indiana University и распространяется свободно. На русском языке не искал, может быть тоже что-то есть.
- Стоп-слова. Тут всё понятно. Слова «и», «но», «по», «из», «под» и так далее, ну никак не влияют на классификацию, так как они встречаются везде. На практике обычно берут некоторое количество самых популярных слов в коллекции и выбрасывают их (числа тоже можно выбросить). Можно просто взять список отсюда.
Подобная обработка — уже устоявшийся способ уменьшения размерности задачи и улучшения производительности.
Метод опорных векторов
Теперь абстрагируемся от текстовых документов и рассмотрим один из существующих алгоритмов классификации.
Не буду здесь грузить деталями и математическими выкладками. Если они интересны, то их можно найти, например, в википедии или на Хабре.
Расскажу вкратце.
Допустим, что у нас есть много точек в n-мерном пространстве, и каждая из точек принадлежит только одному из двух классов. Если мы сможем разделить их как-то на два множества гиперплоскостью размерностью n-1, то это сразу решит проблему. Так случается не всегда, но если множество линейно разделимо то нам повезло:

Классификатор работает тем лучше, чем больше расстояние от разделяющей гиперплоскости до ближайшей точки множества. Нам нужно найти именно такую гиперплоскость из всех возможных. Она называется оптимальной разделяющей гиперплоскостью:

Для поиска используется простоя идея: построить две параллельные гиперплоскости, между которыми нет никаких точек множества и максимизировать расстояние между ними. Ближайшие к параллельным гиперплоскостям точки называются опорными векторами, которые и дали название методу.
А что делать, если множества не является линейно-разделимым? Тем более, что скорее всего это так. В этом случае, мы просто позволяем классификатору делить множества так, чтобы между гиперплоскостями могли оказываться точки (отсюда появляется погрешность классификатора, которую мы пытаемся минимизировать). Найдя такую гиперплоскость, классификация становится делом техники: надо посмотреть с какой стороны от гиперплоскости оказался вектор, класс которого нужно определить.
Готовая реализация
Конечно, можно реализовать алгоритм самому. Но если есть хорошие готовые решения, то это может привести к трате большого количества времени, и не факт что Ваша реализация окажется лучше или хотя бы такой же.
Есть отличная реализация support vector machine под названием SVM light. Она создана в Техническом Университете Дортмунда и распространяется бесплатно (только для исследовательских целей). Есть несколько вариантов реализации (например, умеющий обучаться на реляционных базах данных), но можно взять самый простой, работающий с текстовыми файлами. Такой классификатор состоит из двух исполняемых файлов — обучающего и классифицирующего модулей.
Обучение
Обучающий модуль принимает на вход текстовый файл с обучающими данными. Файл должен содержать вектора с меткой +1 или -1 в зависимости от того, какому из двух классов он принадлежит.
Выглядит это так:
-1 0 0 0 0 0 0 6 0 0 0 6.56 0 0 0 0 0 0 0 45.56 0 0 0 0 0 0.5 0 0 0 0 0 0 0
Так же модуль поймет и такую запись:
-1 7:6 11:6.56 19:45.56 25:0.5 (то есть можно перечислить только ненулевые значения с указанием индекса).
Классификация
Второй модуль принимает на вход текстовый файл с данными, которые нужно классифицировать. Формат такой же, что и для обучения. После классификации создается res.txt в котором записаны результаты.
svm для классификации документов
Теперь разберемся, как можно применить svm к классификации документов. Откуда взять вектора? Как определить к каким категориям относится наш документ, если всего их 80, а svm умеет определять только принадлежность к одному из двух классов?
Документ — это вектор
Представить документ в виде вектора не сложно. Сначала нужно сделать словарь коллекции — это список всех слов, которые в этой коллекции встречаются (для коллекции RCV1 это 47 000 слов). Количество слов и будет размерностью векторов. После этого документ представляется в виде вектора, где i-тый элемент это мера вхождения i-того слова словаря в документ. Это может быть + 1 или -1 в зависимости от того, входит ли слово в документ или нет, или количество вхождений. Или «доля» этого слова в документе. Вариантов много. В итоге получаются вектора большой размерности, где большая часть элементов — нули.
80 категорий — 80 классификаторов
Если у нас 80 категорий, нам нужно запустить классификатор 80 раз. Точнее, у нас должно быть 80 классификаторов для каждой категории, умеющих определять попадает ли документ в эту категорию или нет.
Тесты. Метрики
Для тестирования классификатора можно использовать часть той же самой коллекции (только тогда не стоит использовать эту часть при обучении) сравнивая результаты классификатора с результатами, полученными вручную.
Для оценки работы классификаторов используются несколько метрик:
- Accuracy = ((r — kr) + kw)/n
Фактически — это точность.
- Precision = kr/n
- Recall = kr/r
Здесь kw — количество документов, которые классификатор неправильно отметил как не относящиеся к искомой категории.
kr — количество документов, которые классификаторов правильно отметил как относящиеся к искомой категории.
r — общее количество документов, относящихся к искомой категории по мнению классификатора.
n — общее количество документов, относящихся к искомой категории.
Из этих метрик Precision и Recall являются самыми важными, так как они показывают как сильно мы ошиблись приписав документу категорию и насколько вообще наш классификатор беспорядочно работает. Чем ближе обе метрике к единице — тем лучше.
И небольшой пример. Составив вектора, взяв как меру слова в документе его «долю» (количество вхождений слова в документ деленное на общее количество слов в документе), и обучив классификатор на 32000 документов и при классификации 3000, получились следующие результаты:
Precision = 0.95
Recall = 0.75
Неплохие результаты, с ними классификатор вполне можно использовать для обработки новых данных.
Ссылки
Про RCV1:
О RCV1
Здесь можно найти коллекцию
Про SVM:
Википедия
Большая статья