Довольно часто программисты в своей работе встречаются с необходимостью работать со случайными числами. Чаще всего случайные числа требуются в задачах моделирования, численного анализа и тестирования, но существует и множество других весьма специфических задач.
Конечно, во всех современных языках программирования есть функция random или её аналоги. Эти функции чаще всего дают действительно хорошие псевдослучайные числа, но мне всегда было интересно, как эти функции работают.
В этом топике я постараюсь объяснить, как работает линейный конгруэнтный метод (который чаще всего используется в функции random), и метод получения случайных чисел с помощью полиномиального счётчика (который часто используется для тестирования аппаратуры).
Сразу стоит сказать, что есть смысл генерировать случайные числа только с равномерным законом распределения, т.к. все остальные распределения можно получить из равномерного путём преобразований, известных из теории вероятности.
Для тех, кто забыл или пока не изучал теорию вероятности, напомню, что в равномерно распределённой последовательности нулей и единиц нули в среднем(!) будут встречаться в 50% случаев. Но это вовсе не значит, что в последовательности из 1000 цифр будет ровно 500 нулей. Более того, в последовательности из 1000 цифр может быть 999 нулей, и вероятность того, что тысячный элемент будет равен нулю по-прежнему остаётся равной 0.5. На первый взгляд это кажется парадоксальным, но важно понимать, что все последовательности равновероятны. Если же мы будем рассматривать достаточно большую совокупность таких последовательностей, то в среднем(!) в каждой из них будет 500 нулей.
Немного вспомнив теорию, мы перейдём к истории. В докомпьютерные времена случайные числа получали, вытаскивая разноцветные мячи из мешков, вытягивая карты, бросая кости. Понятно, что серьёзные исследования так проводить было нельзя, поэтому в 1927 года Типпетт опубликовал первую таблицу случайных чисел. Чуть позже люди попытались как-то автоматизировать этот процесс. Начали появляться машины, генерирующие случайные числа. Сейчас такие устройства тоже используются и называются источниками (генераторами) энтропии. Стоит заметить, что только такие устройства могут давать по-настоящему случайные числа. Но, к сожалению, генераторы энтропии довольно дороги, и не представляется возможным установить их в каждый ПК. Именно поэтому и возникла необходимость в алгоритмах получения случайных чисел.
Некоторые люди думают, что получать случайные числа легко. По их мнению для этого достаточно делать случайные сложные математические действия над исходным числом. Если мы откроем второй том всем известного Кнута, то узнаем, что в 1959 Кнут тоже пробовал построить генератор, основанный на такой идее. Его алгоритм выглядел так:
К1. [Выбрать число итераций.] Присвоить Y наибольшую значащую цифру Х. (Мы выполним шаги К2-К13 точно Y+1 раз, т. е. применим рандомизированные преобразования случайное число раз.)
К2. [Выбрать случайный шаг] Присвоить следующую наибольшую значащую цифру X. Переходим к шагу К(3 + Z), т. е. к случайно выбранному шагу в программе.
КЗ. [Обеспечить > 5 х 109] Если X < 5000000000, присвоить X значение X + 5000000000.
К4. [Средина квадрата.] Заменить X серединой квадрата X.
К5. [Умножить.] Заменить X числом (1001001001 X) mod 1010.
К6. [Псевдодополнение.] Если X < 100000000, то присвоить X значение X + 9814055677; иначе присвоить X значение 1010- X.
К7. [Переставить половины.] Поменять местами пять младших по порядку знаков со старшими.
К8. [Умножить.] Выполнить шаг К5.
К9. [Уменьшить цифры.] Уменьшить каждую не равную нулю цифру десятичного представления числа X на единицу.
К10. [Модифицировать на 99999.] Если А' < 105, присвоить X значение — X 2 +99999; иначе присвоить X значение X — 99999.
К11. [Нормировать.] (На этом шаге А' не может быть равным нулю.) Если X <109, то умножить X на 10.
К12. [Модификация метода средин квадратов.] Заменить Х на средние 10 цифр числа Х(Х — 1).
К13. [Повторить?] Если Y > 0, уменьшить У на 1 и возвратиться к шагу К2. Если Y = 0, алгоритм завершен. Значение числа X, полученное на предыдущем шаге, и будет желаемым «случайным» значением.
Несмотря на кажущуюся сложность, этот алгоритм быстро сошёлся к числу 6065038420, которое через небольшое число шагов преобразовалось в себя же. Мораль этой истории в том, что нельзя использовать случайный алгоритм для получения случайных чисел.
В большинстве языков программирования именно этот метод используется в стандартной функции получения случайных чисел. Впервые этот метод был предложен Лехмером в 1949 году. Выбирается 4 числа:
Последовательность получается с использование следующей рекуррентной формулы: Xn+1=(a* Xn+c) mod m.
Этот метод даёт действительно хорошие псевдослучайные числа, но, если взять числа m,a,c произвольно, то результат нас скорее всего разочарует. При m=7, X0=1, a=2, c=4 получится следующая последовательность: 1,6,2,1,6,2,1,…
Очевидно, что эта последовательность не совсем подходит под определение случайной. Тем не менее, этот провал позволил нам сделать два важных вывода:
На самом деле любая функция, отображающая конечное множество X в X, будет давать циклически повторяемый значения. Т.о. наша задача состоит в том, чтобы максимально удлинить уникальную часть последовательности (кстати, очевидно, что длина уникальной части не может быть больше m).
Не вдаваясь в подробности доказательств, скажем, что период последовательности будет равен m только при выполнении следующих трех условий:
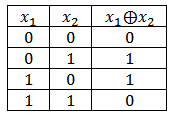
В основе алгоритма, который мы сейчас рассмотрим, лежит операция исключающего ИЛИ (сумма по модулю два). На всякий случай, напомню, как выглядит таблица истинности для данной функции:
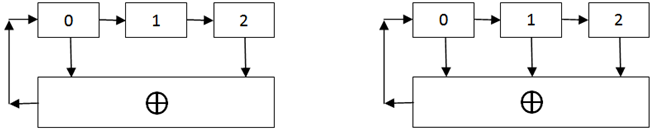
Схемы, представленные на рисунке ниже, являются простейшими полиномиальными счётчиками. Нулевой бит в таких схемах вычисляется на основе функции исключающего ИЛИ, а все остальные биты получаются простым сдвигом. Разряды с которых сигнал идёт на исключающее ИЛИ называются отводами.
Рассмотрим, как будут изменяться значения в этих регистрах при начальном значении 001:
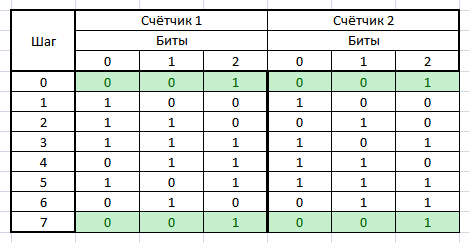
Оба регистра начинают работу с одного и того же значения, но потом значения, генерируемые регистрами начинают быстро расходиться. Но через 6 шагов, оба регистра возвращаются в исходное состояние.
Легко показать, что оба этих регистра сгенерировали максимально длинную последовательность, которая содержит все комбинации, кроме нулевой. Т.е. при разрядности регистра m, можно получить последовательность длинной 2m-1.
Полиномиальный счётчик любой разрядности имеет ряд комбинаций отводов, которые обеспечат последовательность максимальной длины, использование неверных комбинаций приведёт к генерации коротких последовательностей. Отдельная и довольно сложная задача – поиск этих комбинаций отводов.
Стоит заметить, что эти комбинации не всегда уникальны. К примеру, для 10-битного счётчика их существует две: [6;9] и [2;9], для шестиразрядного счётчика таких комбинаций двадцать восемь.
Для того, чтобы найти эти комбинации, необходимо представить счётчик в виде полинома. Счётчики из примера будут иметь следующий вид: x2 XOR 1 и x2 XOR x XOR 1.
Из теории известно, что необходимым и достаточным условием генерации полной последовательности является примитивность характеристического полинома. Это значит, что:
Преимуществами полиномиального счётчика является простота, как программной, так и аппаратной реализации, скорость работы и криптографическая стойкость.
Надеюсь, эта статья была полезной для вас.
Конечно, во всех современных языках программирования есть функция random или её аналоги. Эти функции чаще всего дают действительно хорошие псевдослучайные числа, но мне всегда было интересно, как эти функции работают.
В этом топике я постараюсь объяснить, как работает линейный конгруэнтный метод (который чаще всего используется в функции random), и метод получения случайных чисел с помощью полиномиального счётчика (который часто используется для тестирования аппаратуры).
Введение
Сразу стоит сказать, что есть смысл генерировать случайные числа только с равномерным законом распределения, т.к. все остальные распределения можно получить из равномерного путём преобразований, известных из теории вероятности.
Для тех, кто забыл или пока не изучал теорию вероятности, напомню, что в равномерно распределённой последовательности нулей и единиц нули в среднем(!) будут встречаться в 50% случаев. Но это вовсе не значит, что в последовательности из 1000 цифр будет ровно 500 нулей. Более того, в последовательности из 1000 цифр может быть 999 нулей, и вероятность того, что тысячный элемент будет равен нулю по-прежнему остаётся равной 0.5. На первый взгляд это кажется парадоксальным, но важно понимать, что все последовательности равновероятны. Если же мы будем рассматривать достаточно большую совокупность таких последовательностей, то в среднем(!) в каждой из них будет 500 нулей.
Немного вспомнив теорию, мы перейдём к истории. В докомпьютерные времена случайные числа получали, вытаскивая разноцветные мячи из мешков, вытягивая карты, бросая кости. Понятно, что серьёзные исследования так проводить было нельзя, поэтому в 1927 года Типпетт опубликовал первую таблицу случайных чисел. Чуть позже люди попытались как-то автоматизировать этот процесс. Начали появляться машины, генерирующие случайные числа. Сейчас такие устройства тоже используются и называются источниками (генераторами) энтропии. Стоит заметить, что только такие устройства могут давать по-настоящему случайные числа. Но, к сожалению, генераторы энтропии довольно дороги, и не представляется возможным установить их в каждый ПК. Именно поэтому и возникла необходимость в алгоритмах получения случайных чисел.
Первая попытка получения ПСП
Некоторые люди думают, что получать случайные числа легко. По их мнению для этого достаточно делать случайные сложные математические действия над исходным числом. Если мы откроем второй том всем известного Кнута, то узнаем, что в 1959 Кнут тоже пробовал построить генератор, основанный на такой идее. Его алгоритм выглядел так:
К1. [Выбрать число итераций.] Присвоить Y наибольшую значащую цифру Х. (Мы выполним шаги К2-К13 точно Y+1 раз, т. е. применим рандомизированные преобразования случайное число раз.)
К2. [Выбрать случайный шаг] Присвоить следующую наибольшую значащую цифру X. Переходим к шагу К(3 + Z), т. е. к случайно выбранному шагу в программе.
КЗ. [Обеспечить > 5 х 109] Если X < 5000000000, присвоить X значение X + 5000000000.
К4. [Средина квадрата.] Заменить X серединой квадрата X.
К5. [Умножить.] Заменить X числом (1001001001 X) mod 1010.
К6. [Псевдодополнение.] Если X < 100000000, то присвоить X значение X + 9814055677; иначе присвоить X значение 1010- X.
К7. [Переставить половины.] Поменять местами пять младших по порядку знаков со старшими.
К8. [Умножить.] Выполнить шаг К5.
К9. [Уменьшить цифры.] Уменьшить каждую не равную нулю цифру десятичного представления числа X на единицу.
К10. [Модифицировать на 99999.] Если А' < 105, присвоить X значение — X 2 +99999; иначе присвоить X значение X — 99999.
К11. [Нормировать.] (На этом шаге А' не может быть равным нулю.) Если X <109, то умножить X на 10.
К12. [Модификация метода средин квадратов.] Заменить Х на средние 10 цифр числа Х(Х — 1).
К13. [Повторить?] Если Y > 0, уменьшить У на 1 и возвратиться к шагу К2. Если Y = 0, алгоритм завершен. Значение числа X, полученное на предыдущем шаге, и будет желаемым «случайным» значением.
Несмотря на кажущуюся сложность, этот алгоритм быстро сошёлся к числу 6065038420, которое через небольшое число шагов преобразовалось в себя же. Мораль этой истории в том, что нельзя использовать случайный алгоритм для получения случайных чисел.
Линейный конгруэнтный метод
В большинстве языков программирования именно этот метод используется в стандартной функции получения случайных чисел. Впервые этот метод был предложен Лехмером в 1949 году. Выбирается 4 числа:
- Модуль m (m>0);
- Множитель a (0<=a<m);
- Приращение c (0<=c<m);
- Начальное значение X0 (0<= X0<m)
Последовательность получается с использование следующей рекуррентной формулы: Xn+1=(a* Xn+c) mod m.
Этот метод даёт действительно хорошие псевдослучайные числа, но, если взять числа m,a,c произвольно, то результат нас скорее всего разочарует. При m=7, X0=1, a=2, c=4 получится следующая последовательность: 1,6,2,1,6,2,1,…
Очевидно, что эта последовательность не совсем подходит под определение случайной. Тем не менее, этот провал позволил нам сделать два важных вывода:
- Числа m,a,c, X0 не должны быть случайными;
- Линейный конгруэнтный метод даёт нам повторяющиеся последовательности.
На самом деле любая функция, отображающая конечное множество X в X, будет давать циклически повторяемый значения. Т.о. наша задача состоит в том, чтобы максимально удлинить уникальную часть последовательности (кстати, очевидно, что длина уникальной части не может быть больше m).
Не вдаваясь в подробности доказательств, скажем, что период последовательности будет равен m только при выполнении следующих трех условий:
- Числа c и m взаимно простые;
- a-1 кратно p для каждого простого p, являющегося делителем m;
- Если m кратно 4, то и a-1 должно быть кратно 4.
Получение псевдослучайных чисел на основе полиномиального счетчика (сдвигового регистра)
В основе алгоритма, который мы сейчас рассмотрим, лежит операция исключающего ИЛИ (сумма по модулю два). На всякий случай, напомню, как выглядит таблица истинности для данной функции:

Схемы, представленные на рисунке ниже, являются простейшими полиномиальными счётчиками. Нулевой бит в таких схемах вычисляется на основе функции исключающего ИЛИ, а все остальные биты получаются простым сдвигом. Разряды с которых сигнал идёт на исключающее ИЛИ называются отводами.

Рассмотрим, как будут изменяться значения в этих регистрах при начальном значении 001:

Оба регистра начинают работу с одного и того же значения, но потом значения, генерируемые регистрами начинают быстро расходиться. Но через 6 шагов, оба регистра возвращаются в исходное состояние.
Легко показать, что оба этих регистра сгенерировали максимально длинную последовательность, которая содержит все комбинации, кроме нулевой. Т.е. при разрядности регистра m, можно получить последовательность длинной 2m-1.
Полиномиальный счётчик любой разрядности имеет ряд комбинаций отводов, которые обеспечат последовательность максимальной длины, использование неверных комбинаций приведёт к генерации коротких последовательностей. Отдельная и довольно сложная задача – поиск этих комбинаций отводов.
Стоит заметить, что эти комбинации не всегда уникальны. К примеру, для 10-битного счётчика их существует две: [6;9] и [2;9], для шестиразрядного счётчика таких комбинаций двадцать восемь.
Для того, чтобы найти эти комбинации, необходимо представить счётчик в виде полинома. Счётчики из примера будут иметь следующий вид: x2 XOR 1 и x2 XOR x XOR 1.
Из теории известно, что необходимым и достаточным условием генерации полной последовательности является примитивность характеристического полинома. Это значит, что:
- Характеристический полином нельзя представить в виде произведения полиномов более низкой степени;
- Характеристический полином является делителем полинома zδ XOR 1, при(δ=2m-1, и не является делителем при любых других значениях δ<2m-1.
Преимуществами полиномиального счётчика является простота, как программной, так и аппаратной реализации, скорость работы и криптографическая стойкость.
Надеюсь, эта статья была полезной для вас.