Возникла задача реализовать на С++ алгоритм скользящего среднего, который находит широкое применение в обработке сигналов и статистике.
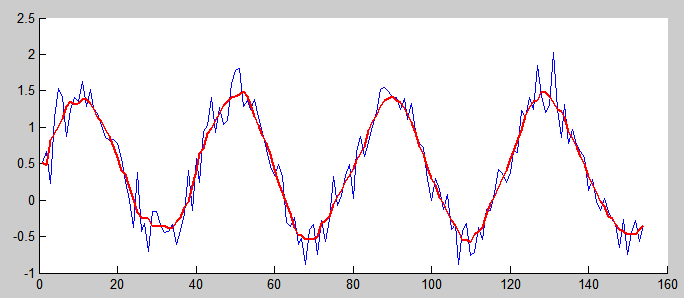
За основу была взята функция smooth в MATLAB.
Данную функцию можно использовать для фильтрации сигналов. В качестве входных параметров определяются массив данных и окно усреднения.
Кому интересно, прошу под кат
Итак, есть несколько реализаций данного алгоритма. Рассмотрим самый простой из них:
предположим, размер окна усреднения будет равен 5, тогда на каждом шаге усреднения берется текущее значение, к нему прибавляются 4 предыдущих и результат делится на 5. Очевидная проблема здесь в инициализации алгоритма, сначала нужно накопить определенное количество данных, не меньшее, чем окно усреднения.
В MATLAB алгоритм фильтрации с помощью скользящего среднего реализован в функции smooth
Пример использования smooth(input,window),
где input — массив входящих данных
window — окно усреднения.
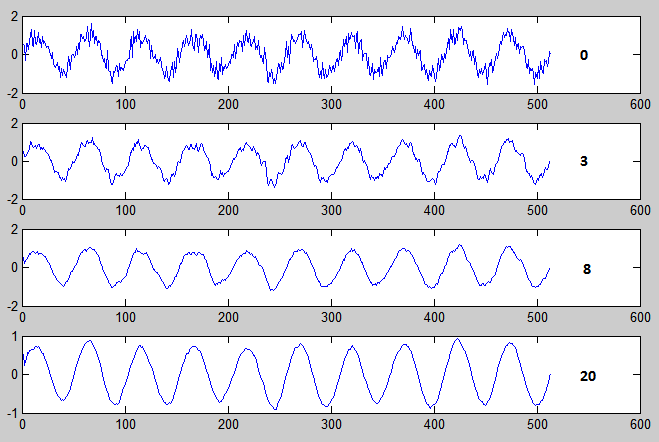
Изменяя параметр window можно получить большую или меньшую степень сглаживания данных:
Исходник, реализующий данный пример представлен ниже:
Для компенсации задержки в обработке сигнала, MATLAB использует динамически изменяемый размер окна, суть метода иллюстрирует следующий пример:
Собственную реализацию данного алгоритма я сначала написал в MATLAB, а затем перенес на С++
MATLAB edition:
Результат работы данной программы абсолютно совпадает с матлабовским smooth при нечетных размерах окна и несколько отличается при четном его значении (четные окна матлаб считает чуть иначе)
Исходный m-файл можно взять тут
С++ Edition
спасибо за внимание, конструктивная критика приветствуется
p.s.:
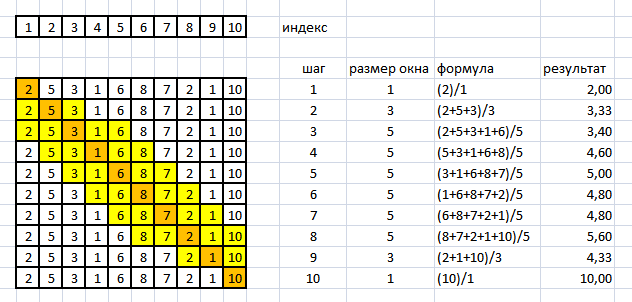
Алгоритм можно оптимизировать по скорости работы изменив подсчет суммы:

Видно, что для подсчета суммы элементов на 4-м шаге нужно из суммы на третьем шаге вычесть 1-й элемент массива (2, отмечен красным) и прибавить 6-й элемент (8, желтая клетка).
На следующем шаге процедура повторяется.
Данный подход будет эффективным при большом размере окна усреднения

За основу была взята функция smooth в MATLAB.
Данную функцию можно использовать для фильтрации сигналов. В качестве входных параметров определяются массив данных и окно усреднения.
Кому интересно, прошу под кат
Итак, есть несколько реализаций данного алгоритма. Рассмотрим самый простой из них:
предположим, размер окна усреднения будет равен 5, тогда на каждом шаге усреднения берется текущее значение, к нему прибавляются 4 предыдущих и результат делится на 5. Очевидная проблема здесь в инициализации алгоритма, сначала нужно накопить определенное количество данных, не меньшее, чем окно усреднения.
В MATLAB алгоритм фильтрации с помощью скользящего среднего реализован в функции smooth
Пример использования smooth(input,window),
где input — массив входящих данных
window — окно усреднения.
Изменяя параметр window можно получить большую или меньшую степень сглаживания данных:

Исходник, реализующий данный пример представлен ниже:
clear all;
%% Параметры
t=1;% длительность сигнала
Fd=512;% Частота дискретизации (Гц)
A1=1;% Амплитуда синусоиды
F1=10;% Частота синусоиды (Гц)
SNR=0.3;% Соотношение сигнал/шум
T=0:1/Fd:t;% Массив отсчетов
Noise=A1*SNR*randn(1,length(T));%Сгенерированный шум
Signal=A1*sind((F1*360).*T);%Сгенерированный сигнал
SN=Signal+Noise;
figure(1);
subplot(4,1,1);
plot(SN);
subplot(4,1,2);
plot(smooth(SN,3));
subplot(4,1,3);
plot(smooth(SN,8));
subplot(4,1,4);
plot(smooth(SN,20));
Для компенсации задержки в обработке сигнала, MATLAB использует динамически изменяемый размер окна, суть метода иллюстрирует следующий пример:

Собственную реализацию данного алгоритма я сначала написал в MATLAB, а затем перенес на С++
MATLAB edition:
%my_smooth
%в случае, если размер окна четный, увеличиваем его на 1 для симметрии;
window = 5;
if(mod(window,2)==0)
window=window+1;
end
hw=(window-1)/2; %размах окна влево и вправо от текущей позиции
n=length(Signal);
result=zeros(n,1);
result(1)=SN(1); %первый элемент берем из исходного массива SN как есть
for i=2:n %организовываем цикл по числу элементов
init_sum = 0;
if(i<=hw) %если индекс меньше половины окна, мы находимся в начале массива,
%нужно брать окно меньшего размера
k1=1; %в качестве начала окна берем первый элемент
k2=2*i-1; %конец окна
z=k2; %текущий размер окна
elseif (i+hw>n) %если индекс+половина окна больше n - мы приближаемся к концу массива и размер окна
%также нужно уменьшать
k1=i-n+i; %начало окна
k2=n; %конец окна - последний элемент массива
z=k2-k1; %размер окна
else %если первые два условия не выполняются, мы в середине массива
k1=i-hw;
k2=i+hw;
z=window;
end
for j=k1:k2 %организуем цикл от начала до конца окна
init_sum=init_sum+SN(j); %складываем все элементы
end
result(i)=init_sum/(z); %и делим на текущий размер окна
end
Результат работы данной программы абсолютно совпадает с матлабовским smooth при нечетных размерах окна и несколько отличается при четном его значении (четные окна матлаб считает чуть иначе)
Исходный m-файл можно взять тут
С++ Edition
void smooth(double *input, double *output, int n, int window)
{
int i,j,z,k1,k2,hw;
double tmp;
if(fmod(window,2)==0) window++;
hw=(window-1)/2;
output[0]=input[0];
for (i=1;i<n;i++){
tmp=0;
if(i<hw){
k1=0;
k2=2*i;
z=k2+1;
}
else if((i+hw)>(n-1)){
k1=i-n+i+1;
k2=n-1;
z=k2-k1+1;
}
else{
k1=i-hw;
k2=i+hw;
z=window;
}
for (j=k1;j<=k2;j++){
tmp=tmp+input[j];
}
output[i]=tmp/z;
}
спасибо за внимание, конструктивная критика приветствуется
p.s.:
Алгоритм можно оптимизировать по скорости работы изменив подсчет суммы:

Видно, что для подсчета суммы элементов на 4-м шаге нужно из суммы на третьем шаге вычесть 1-й элемент массива (2, отмечен красным) и прибавить 6-й элемент (8, желтая клетка).
На следующем шаге процедура повторяется.
Данный подход будет эффективным при большом размере окна усреднения