Sqrt-декомпозиция — это метод, или структура данных, позволяющая в режиме онлайн проводить такие операции, как подсчет суммы на отрезке за  и обновление элемента за
и обновление элемента за  . Существуют более эффективные структуры, такие как дерево фенвика или дерево отрезков, которые оба запроса обрабатывают за
. Существуют более эффективные структуры, такие как дерево фенвика или дерево отрезков, которые оба запроса обрабатывают за  . Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.
. Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.

Пусть нам задан массив A[i], на который поступают запросы вида:
Мы можем предрасчитать массив частичных сумм, а именно: . Однако на запрос изменения, потребует пересчета частичных сумм (содержащих этот элемент) и в худшем случае составит асимптотику порядка
. Однако на запрос изменения, потребует пересчета частичных сумм (содержащих этот элемент) и в худшем случае составит асимптотику порядка 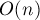 , что не есть хорошо.
, что не есть хорошо.
Основной идеей будет то, что *
*  =
=  . А именно, если у нас есть
. А именно, если у нас есть  элементов, то всех их мы можем разбить на
элементов, то всех их мы можем разбить на  блоков, где каждый длиной
блоков, где каждый длиной  , кроме, может быть, последнего. Затем для всех блоков мы посчитаем сумму чисел на нем, сразу можно увидеть, что вспомогательный массив будет занимать
, кроме, может быть, последнего. Затем для всех блоков мы посчитаем сумму чисел на нем, сразу можно увидеть, что вспомогательный массив будет занимать  памяти.
памяти.
Опишем построение массива sqrtSums[]:
Рассмотрим запрос суммы [L; R], для «быстрого» ответа на него, необходимо максимально использовать уже имеющуюся информацию. Как мы уже говорили, Sum[L; R] = Sum[0, R] — Sum[0; L-1]. Осталось научиться обрабатывать запрос Sum[0; R]. Заметим, что несколько первых отрезков , так как отрезков всего
, так как отрезков всего  ). Однако у нас останется «хвостик» вида:
). Однако у нас останется «хвостик» вида:  , не повлияет). Приведем пример реализации:
, не повлияет). Приведем пример реализации:
Во многих структурах, для реализации данного запроса, требуется опуститься по дереву, или посчитать хеш-функцию, или еще что-то… Однако тут нам необходимо поменять всего 2 значения (каждый элемент входит в ровно один «sqrt-отрезок»)
Чтобы отвечать на запросы RMQ(Range Min / Max Query) нужно почти тоже самое, что и для сумм. Однако стоит отметить, чтобы обновить элемент «в тупую», нам потребуется времени (при обновлении элемента, пересчитывать min/max на всем «sqrt-отрезке»), но если наложить на обновления некоторые ограничения, то мы добьемся оценки
времени (при обновлении элемента, пересчитывать min/max на всем «sqrt-отрезке»), но если наложить на обновления некоторые ограничения, то мы добьемся оценки  . А именно, при решении задачи поиска минимума/максимума, разрешать только уменьшать/увеличивать элемент.
. А именно, при решении задачи поиска минимума/максимума, разрешать только уменьшать/увеличивать элемент.
Код для обновления минимума:
Аналогично для обновления максимума:
Нужно добавить, что в задаче RMQ, задача не сводится к [0; R] — [0; L-1], т.е. придется вычислять минимум/максимум с L по R (не считая заново, полностью входящие в [L; R] «sqrt-отрезки», подумайте, почему асимптотика не поменяется, а чистое время работы может даже улучшится...).
Для вычисления GCD (Greatest Common Divisor), мы не сможем использовать ту «фишку», что мы провернули для min/max. Поэтому обе операции вычисляются за .
.
Код для GCD (для минимума и максимума функции getGCD заменятся на min/max):
Пользовался этим сайтом, а именно.
Так как вдохновила на статью лекция из Харьковской Зимней Компьютерной Школы, то кину сайт, возможно скоро там появится сборник за этот год, с видео-лекциями.
Пока все, надеюсь, что было понятно.
 . Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа.
. Однако я хочу рассказать про корневую оптимизацию, т.к. в этом методе заложена идея, применимая к задачам другого типа. 
Постановка задачи
Пусть нам задан массив A[i], на который поступают запросы вида:
- посчитать сумму на отрезке [L; R] (позже, мы поймем, что аналогично можно вычислять функции min, max, gcd и др.
- добавить к элементу A[i], delta
Наивная реализация
Мы можем предрасчитать массив частичных сумм, а именно:
for(int j = 0; j < i; j++) B[j] += A[i];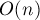 , что не есть хорошо.
, что не есть хорошо. Построение декомпозиции
Основной идеей будет то, что
Опишем построение массива sqrtSums[]:
int len = (int)sqrt(n) + 1; //длина каждого "sqrt-отрезка"
int sqrtSums[MAXN], st = 0; //массив предпросчитанных сумм
for(int i = 0; i < n; i++)
sqrtSums[i / len] += A[i];
Описание запросов
Запрос суммы (RSQ)
Рассмотрим запрос суммы [L; R], для «быстрого» ответа на него, необходимо максимально использовать уже имеющуюся информацию. Как мы уже говорили, Sum[L; R] = Sum[0, R] — Sum[0; L-1]. Осталось научиться обрабатывать запрос Sum[0; R]. Заметим, что несколько первых отрезков
([0; len-1], [len; 2*len-1], ...) будут полностью входить в запрос [0; R], а значит мы можем использовать информацию из sqrtSums[] (за [k*len; k*len + delta] (delta < len, т.к. иначе, мы сможем включить еще один отрезок [k*len; (k+1)*len-1]), его мы сможем посчитать вручную (delta < len, на асимптотику,
int getPartSum(int r)
{
int it = 0, res = 0;
while((it+1) * len -1 <= r)
res += sqrtSums[it++]; //прибавляем предпосчитанные отрезки, пока можем
for(int i = it*len; i <=r; i++)
res += A[i]; //прибавляем "хвост"
return res;
}
int getSum(int l, int r)
{
if(l == 0)
return getPartSum(r);
else
return getPartSum(r) - getPartSum(l-1);
}
Запрос на изменение элемента
Во многих структурах, для реализации данного запроса, требуется опуститься по дереву, или посчитать хеш-функцию, или еще что-то… Однако тут нам необходимо поменять всего 2 значения (каждый элемент входит в ровно один «sqrt-отрезок»)
int incElement(int index, int delta)
{
A[index] += delta;
sqrtSums[index/len] += delta;
}
Range Min/Max/Gcd Query
Чтобы отвечать на запросы RMQ(Range Min / Max Query) нужно почти тоже самое, что и для сумм. Однако стоит отметить, чтобы обновить элемент «в тупую», нам потребуется
Код для обновления минимума:
int decElement(int index, unsigned int delta) //delta - на сколько уменьшить элемент
{
A[index] -= delta;
sqrtSums[index/len] = min(sqrtSums[index/len], A[index]);
}
Аналогично для обновления максимума:
int incElement(int index, unsigned int delta) //delta - на сколько увеличить элемент
{
A[index] += delta;
sqrtSums[index/len] = max(sqrtSums[index/len], A[index]);
}
Нужно добавить, что в задаче RMQ, задача не сводится к [0; R] — [0; L-1], т.е. придется вычислять минимум/максимум с L по R (не считая заново, полностью входящие в [L; R] «sqrt-отрезки», подумайте, почему асимптотика не поменяется, а чистое время работы может даже улучшится...).
Для вычисления GCD (Greatest Common Divisor), мы не сможем использовать ту «фишку», что мы провернули для min/max. Поэтому обе операции вычисляются за
Код для GCD (для минимума и максимума функции getGCD заменятся на min/max):
int getGCD(int a, int b)
{
while(a && b)
{
if(a < b)
b %= a;
else
a %= b;
}
return a + b;
}
int gcdRQ(int l, int r)
{
int cur_gcd = A[l++];
for(int i = l; i <= r;)
if (i % len == 0 && i + len - 1 <= r) {
cur_gcd = getGCD(cur_gcd, b[i / len]);
i += len; //перескок через "sqrt-отрезок"
}
else
cur_gcd = getGCD(cur_gcd, A[i++]);
}
Источники
Пользовался этим сайтом, а именно.
Так как вдохновила на статью лекция из Харьковской Зимней Компьютерной Школы, то кину сайт, возможно скоро там появится сборник за этот год, с видео-лекциями.
Пока все, надеюсь, что было понятно.