… или как я получил «Аленку» за консольное приложение
Существует довольно распространённое мнение, что выполнение различных тестовых заданий помогает очень быстро поднять свой профессиональный уровень. Я и сам люблю иногда откопать какое-нить мудреное тестовое и порешать его, чтобы быть постоянно в тонусе, как говорится. Как-то я выполнял конкурсное задание на стажировку в одну компанию, задачка показалась мне забавной и интересной, вот её краткий текст:
Представьте, что ваш коллега-нытик пришел рассказать о своей непростой задаче — ему нужно не просто упорядочить по возрастанию набор целых чисел, а выдать все элементы упорядоченного набора с L-го по R-й включительно!
Вы заявили, что это элементарная задача и, чтобы написать решение на языке C#, вам нужно десять минут. Ну, или час. Или два. Или шоколадка «Алёнка»
Предполагается, что в наборе допускаются дубликаты, и количество элементов будет не больше, чем 10^6.
К оценке решения есть несколько комментариев:
Ваш код будут оценивать и тестировать три программиста:Решение может быть очень интересным, поэтому я посчитал нужным его описать.
- Билл будет запускать ваше решение на тестах размером не больше 10Кб.
- В тестах Стивена количество запросов будет не больше 10^5, при этом количество запросов на добавление будет не больше 100.
- В тестах Марка количество запросов будет не больше 10^5.
Решение
Пусть у нас есть абстрактное хранилище.
Обозначим Add(e) — добавление элемента в хранилище, а Range(l, r) — взятие среза с l по r элемент.
Тривиальный вариант хранилища может быть таким:
- Основой хранилища будет упорядоченный по возрастанию динамический массив.
- При каждой вставке бинарным поиском находится позицию, в которую необходимо вставить элемент.
- При запросе Range(l, r) будем просто брать срез массива из l по r.
C Range(l, r) — взятие среза можно оценить, как O(r — l).
C Add(e) — вставка в худшем случае будет работать за O(n), где n — количество элементов. При n ~ 10^6, вставка — узкое место. Ниже в статье будет предложен улучшенный вариант хранилища.
Пример исходного кода можно посмотреть здесь.
Более подходящий вариант может быть, например таким:
- Основой хранилища будет самобалансирующееся дерево поиска, имеющее сложность O(ln n) на операцию вставки, поиска, удаления(AVL tree, RB tree и другие).
- Расширяется структура данных путем добавления в узел информации о количестве узлов в поддереве. Это необходимо для того, чтобы получать i-ый элемент дерева за O(ln n).
- Переписывается добавление элемента в дерево, чтобы пересчитывать количество узлов в поддереве. Это можно сделать так, что стоимость операции добавления останется O(ln n).
Skiplist
Skiplist — это рандомизированная альтернатива деревьям поиска, в основе которой лежит несколько связных списков. Была изобретена William Pugh в 1989 году. Операции поиска, вставки и удаления выполняются за логарифмически случайное время.
Эта структура данных не получила широкой известности (кстати, и на хабре достаточно обзорно о ней написано), хотя у нее хорошие асимптотические оценки. Любопытства ради захотелось ее реализовать, тем более имелась подходящая задача.
Дальше я приведу краткую выжимку из всех источников, которыми я пользовался для решения.
Пусть у нас есть отсортированный односвязный список:

В худшем случае поиск выполняется за O(n). Как его можно ускорить?
В одной из видео-лекций, которые я пересматривал, когда занимался задачкой, приводился замечательный пример про экспресс-линии в Нью-Йорке:

- Скоростные линии соединяют некоторые станции
- Обычные линии соединяют все станции
- Есть обычные линии между общими станциями скоростных линий
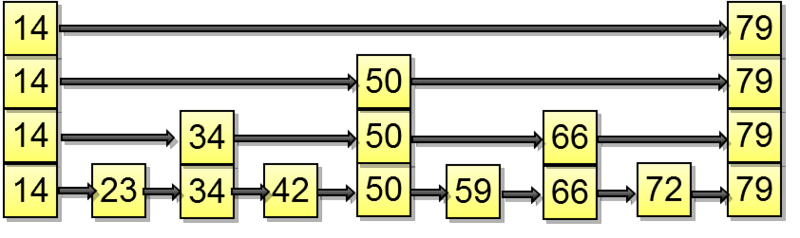
На примере изображен идеальный SkipList, в реальности всё выглядит подобным образом, но немного не так :)
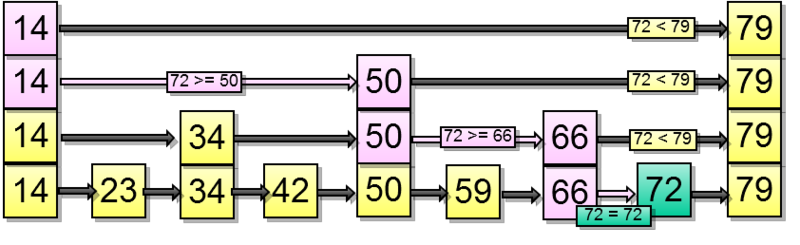
Поиск
Так происходит поиск. Предположим, что мы ищем 72-й элемент:
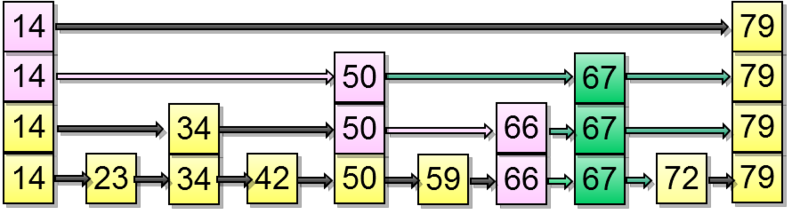
Вставка
Со вставкой все немного сложнее. Для того чтобы вставить элемент, нам необходимо понять, куда его вставить в самом нижнем списке и при этом протолкнуть его на какое-то количество вышележащих уровней. Но на какое количество уровней нужно проталкивать каждый конкретный элемент?
Решать это предлагается так: при вставке мы добавляем новый элемент в самый нижний уровень и начинаем подкидывать монетку, пока она выпадает, мы проталкиваем элемент на следующий вышележащий уровень.
Попробуем вставить элемент — 67. Сначала найдем, куда в нижележащем списке его нужно вставить:

Предположил, что монетка выпала два раза подряд. Значит нужно протолкнуть элемент на два уровня вверх:
Доступ по индексу
Для доступа по индексу предлагается сделать следующее: каждый переход пометить количеством узлов, которое лежит под ним:

После того, как мы получаем доступ к i-му элементу (кстати, получаем мы его за O(ln n)), сделать срез не представляется трудным.
Пусть необходимо найти Range(5, 7). Сначала получим элемент по индексу пять:

А теперь Range(5, 7):

О реализации
Кажется естественной реализация, когда узел SkipList выглядит следующим образом:
SkipListNode {
int Element;
SkipListNode[] Next;
int [] Width;
}
Но в C# в массиве хранится еще и его длина, а хотелось сделать это за как можно меньшее количество памяти (как оказалось, в условиях задачи все оценивалось не так строго). При этом хотелось сделать так, чтобы реализация SkipList и расширенного RB Tree занимала примерно одинаковое количество памяти.
Ответ, как уменьшить потребление памяти, неожиданно был найден при ближайшем рассмотрении ConcurrentSkipListMap из пакета java.util.concurrent.
Двумерный skiplist
Пусть в одном измерении будет односвязный список из всех элементов. Во втором же будут лежать «экспресс-линии» для переходов со ссылками на нижний уровень.
ListNode {
int Element;
ListNode Next;
}
Lane {
Lane Right;
Lane Down;
ListNode Node;
}Нечестная монетка
Еще для снижения потребления памяти можно воспользоваться «нечестной» монеткой: уменьшить вероятность проталкивания элемента на следующий уровень. В статье William Pugh рассматривался срез из нескольких значений вероятности проталкивания. При рассмотрении значений ½ и ¼ на практике получилось примерно одинаковое время поиска при уменьшении потребления памяти.
Немного о генерации случайных чисел
Копаясь в потрохах ConcurrentSkipListMap, заметил, что случайные числа генерируются следующим образом:
int randomLevel() {
int x = randomSeed;
x ^= x << 13;
x ^= x >>> 17;
randomSeed = x ^= x << 5;
if ((x & 0x80000001) != 0)
return 0;
int level = 1;
while (((x >>>= 1) & 1) != 0) ++level;
return level;
}Исходник получившегося хранилища можно глянуть здесь.
Все вместе можно забрать с googlecode.com (проект Pagination).
Тесты
Было использовано три типа хранилища:
- ArrayBased (динамический массив)
- SkipListBased (SkipList c параметром ¼)
- RBTreeBased (красно-черное дерево: реализация моего знакомого, который выполнял аналогичное задание).
- Упорядоченные по возрастанию элементы
- Упорядоченные по убыванию элементы
- Случайные элементы
Результаты:
| Array | RBTree | SkipList | |
|---|---|---|---|
| Random | 127033 ms | 1020 ms | 1737 ms |
| Ordered | 108 ms | 457 ms | 536 ms |
| Ordered by descending | 256337 ms | 358 ms | 407 ms |
Также были проведены замеры: сколько каждое хранилище занимает в памяти при вставленных в него 10^6 элементах. Использовался студийный профайлер, для простоты запускался такой код:
var storage = ...
for(var i = 0; i < 1000000; ++i)
storage.Add(i);
| Array | RBTree | SkipList | |
|---|---|---|---|
| Total bytes allocated | 8,389,066 bytes | 24,000,060 bytes | 23,985,598 bytes |
Хеппи-энд с «Алёнкой»
Коллега-нытик, по условию задачи, проспорил мне шоколадку. Моё решение зачли с максимальным баллом. Надеюсь, кому-нибудь данная статья будет полезна. Если есть какие-то вопросы — буду рад ответить.
P.S.: я был на стажировке в компании СКБ Контур. Это чтобы не отвечать на одинаковые вопросы =)