 Листая страницы хаба «Алгоритмы», наткнулся на топик, посвященный решению задачи локализации точки в многоугольнике: задан многоугольник (замкнутая ломаная линия без самопересечений), требуется определить — находится ли заданная точка A внутри этого многоугольника или нет. В одном из последних комментариев к топику было высказано недоумение, какое отношение такая чисто математическая задача имеет к теории алгоритмов. Имеет-имеет, причем самое непосредственное. Задача локализации является классической задачей вычислительной геометрии (не путать с компьютерной графикой). В качестве разминки предлагается взглянуть на картинку справа, на которой изображен многоугольник типа кривой Пеано (источник [1]), и попытаться ответить на вопрос — красная точка
Листая страницы хаба «Алгоритмы», наткнулся на топик, посвященный решению задачи локализации точки в многоугольнике: задан многоугольник (замкнутая ломаная линия без самопересечений), требуется определить — находится ли заданная точка A внутри этого многоугольника или нет. В одном из последних комментариев к топику было высказано недоумение, какое отношение такая чисто математическая задача имеет к теории алгоритмов. Имеет-имеет, причем самое непосредственное. Задача локализации является классической задачей вычислительной геометрии (не путать с компьютерной графикой). В качестве разминки предлагается взглянуть на картинку справа, на которой изображен многоугольник типа кривой Пеано (источник [1]), и попытаться ответить на вопрос — красная точка Понятно, что если под многоугольником понимается треугольник или четырехугольник, то никаких алгоритмов в полном смысле этого слова не возникает, а возникают три-четыре формулы, которые и надо запрограммировать. Однако, совсем другая история начинается, если число вершин многоугольника оказывается большим. Например, миллион или сто миллионов вершин. Такая задача кажется уже вполне себе алгоритмической. Наивный алгоритм (запуск луча из заданной точки и подсчет числа его пересечений со сторонами многоугольника) является линейным по числу вершин многоугольника n, т.к. мы должны проверить пересечение луча со всеми сторонами многоугольника. Соответственно возникает вопрос, а можно ли сделать это быстрее, т.е. имеется ли сублинейный алгоритм решения задачи локализации в данной постановке? Правильный ответ на этот вопрос — да, задача может быть решена за время O(log2n). Подробности решения в общем случае, когда многоугольник не обязан быть выпуклым, можно найти в замечательной книжке [2]. А ниже мы рассмотрим, как можно применить алгоритм двоичного поиска к задаче локализации точки в выпуклом многоугольнике.
Небольшой ликбез
Пусть заданы три точки A, B и C. Предположим, что мы смотрим из точки A в точку B. Где при этом окажется точка C — справа или слева относительно направления нашего взгляда? Ответить на этот вопрос можно с помощью векторного произведения векторов a=AB и b=BC, точнее с помощью z-координаты такого произведения, которая вычисляется по простой формуле z=axby-aybx. Если z>0, то искомый поворот левый, если z<0 — то правый. Если же
Код на питоне, вычисляющий направление поворота, элементарен (точки представляются списками длины 2):
def rotate(A,B,C):
return (B[0]-A[0])*(C[1]-B[1])-(B[1]-A[1])*(C[0]-B[0])
Имея такую полезную функцию, можно делать много добрых дел. Например, можно определять, пересекаются ли два заданных отрезка AB и CD? Это, кстати, еще одна базовая операция вычислительной геометрии, и нам она тоже скоро понадобится (правда, всего один раз). Идея простая — два отрезка пересекаются тогда и только тогда, когда концы одного отрезка лежат по разные стороны другого и наоборот.
def intersect(A,B,C,D):
return rotate(A,B,C)*rotate(A,B,D)<=0 and rotate(C,D,A)*rotate(C,D,B)<0
Причиной такого странного выбора знаков неравенств является особенность будущего применения данной функции (в частности, точки A, B и C будут различными вершинами выпуклого многоугольника, а точка D — точкой, которую мы пытаемся локализовать).
Двоичный поиск
Теперь переходим собственно к локализации. Заданы выпуклый многоугольник P, состоящий из n вершин и точка A. При этом предполагается, что вершины в P пронумерованы против часовой стрелки (говорят, что направление обхода по периметру P положительно).
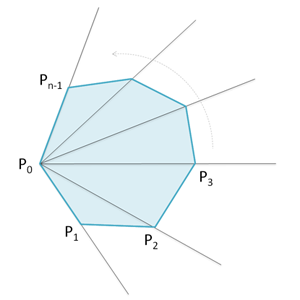
Идея алгоритма: возьмем первую вершину многоугольника P0 и попытаемся определить, в какой сегмент (угол) PiP0Pi+1 попадает точка A. Для начала проверим, что A попадает в сегмент Pn-1P0P1, если это не так, то A гарантированно лежит вне многоугольника.

Код:
def pointloc(P,A):
n = len(P)
if rotate(P[0],P[1],A)<0 or rotate(P[0],P[n-1],A)>0:
return False
Дальше все как в классическом двоичном поиске — полагаем p=1, r=n-1 (границы текущего сегмента), вычисляем среднюю вершину q=(p+r)/2, смотрим, где находится A относительно вектора P0Pq, если слева, то заменяем r на q, если справа, то заменяем p на q.

Продолжаем этот процесс, пока не окажется, что r-p=1:
p, r = 1, n-1
while r-p>1:
q = (p+r)/2
if rotate(P[0],P[q],A)<0: r = q
else: p = q
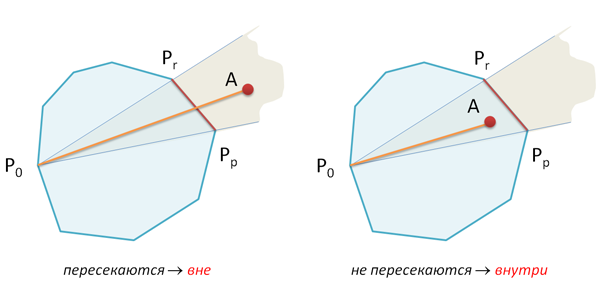
Теперь осталось проверить, пересекаются ли отрезки P0A и PpPr?
Если пересекаются, то точка A лежит вне, если не пересекаются, то внутри.
Код:
return not intersect(P[0],A,P[p],P[r])
Вот собственно и все…
Итоги
Нетрудно убедиться, что сложность алгоритма такая же, как и у классического алгоритма двоичного поиска — O(log2n). И все было бы замечательно, если бы этот алгоритм не был заточен под выпуклые многоугольники. Справедливости ради, рассмотренный нами алгоритм работает и с некоторыми невыпуклыми многоугольниками, но весьма специфического вида — в таких многоугольниках все диагонали, ведущие из нулевой вершины должны лежать внутри многоугольника:
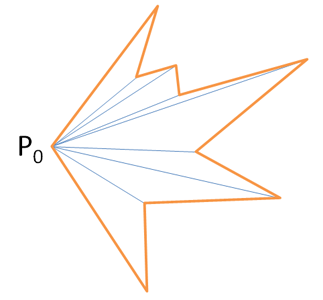
Универсальный алгоритм локализации также работает на принципе двоичного поиска, только внутри у него все устроено, мягко говоря, немного сложнее.
Спасибо за внимание!
PS: Задача с картинкой вверху топика легко решается в любом графическом редакторе: выбираем инструмент заливка (fill), берем цвет отличный от фона, кликаем по краю картинки (вне многоугольника) и вуаля!