В обычной жизни мы обычно пользуемся позиционной системой счисления. В позиционной системе счисления значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда) [1]. Однако существуют и так называемые «непозиционные системы счисления», к одной из которых относится «система остаточных классов» (СОК) (или в оригинале Residue Number System (RNS)), являющаяся основой модулярной арифметики. Модулярная арифметика базируется на «Китайской теореме об остатках» [2], которая для нашего случая звучит следующим образом:
На первый взгляд непонятно какое преимущество может дать такая система, однако существует 2 свойства, которые позволяют эффективно использовать модулярную арифметику в некоторых областях микроэлектроники:
Но не всё так гладко, как хотелось бы. В отличие от позиционной системы счисления, следующие операции (называемые «немодульными») выполняются сложнее, чем в позиционной системе счисления: сравнение чисел, контроль переполнения, деление, квадратный корень и.т.д. Первые успешные попытки применения модулярной арифметики в микроэлектронике были предприняты ещё в 1950-х годах, но из-за сложностей с немодульными операциями интерес несколько утих. Однако в настоящее время модулярная арифметика снова возвращается в микроэлектронику по следующим причинам:
В данный момент модулярная арифметика применяется в следующих областях: цифровая обработка сигналов, криптография, обработка изображений/аудио/видео и.т.д.
Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.
Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p
Любое число X можно записать в виде X%p = (xn-1*2n-1 + xn-2*2n-2 + x0*20)%p = ((xn-1)%p*2n-1%p) + ((xn-2)%p*2n-2%p) + … + x0%p)%p. Поскольку в данном случае xn-1, … x0 равны 0 или 1, то фактически нам требуется сложить вычеты вида (2i%p).
Систему используемых модулей подбирают под конкретную задачу. Например, для представления 32-х битных чисел достаточно следующей системы модулей: (7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом, их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит, то есть операции сложения и умножения будут производиться над 5-битными числами.
Особое значение так же имеет система модулей вида: (2n-1, 2n, 2n+1) в связи с тем, что прямое и обратное преобразование для них выполняется простейшим образом. Что бы получить остаток от деления на 2n достаточно взять последние n цифр двоичного представления числа.
Обратное преобразование из системы счисления в остаточных классах в позиционную систему счисления производится одним из двух способов:
Остальные предложенные в различной литературе способы, по сути, являются смесью этих двух.
Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x1, x2, … xn) = (x1, 0, …, 0) + (0, x2, …, 0) + … + (0, 0, …., xn) = x1*(1, 0, …, 0) + x2*(0, 1, …, 0) + … + xn*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (Mi*bi)%pi = 1, где Mi = M/pi, а bi – искомое число. В этом случае позиционное представление Bi = Mi*bi и
X = (x1*(M1*b1) + x2*(M2*b2) + … + xn*(Mn*bn))%M
Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M1, …, Mn), а так же операция взятия остатка по модулю большого числа M.
Способ на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел p1, … pn, как [4]:
X = a1 + a2*p1 + a3*p1*p2 +… + an-1*p1*p2*…*pn-2 + an*p1*p2*…*pn-1, где 0 < ai < pi
Для использования этого метода требуются константы вида (pi-1)%pk-1. Можно также заметить, что начинать вычисление a3 можно, как только появилось значение a1. На основе этого метода можно строить конвеерные преобразователи.
Статья написана несколько сумбурно, потому что тема достаточно большая и в одну статью вместить все не представляется возможным. В следующих статьях я попробую расписать более подробно различные аспекты модулярной арифметики. На Хабре же я не нашел вообще ничего что относится к этой теме, только краткие упоминания в других статьях, поэтому и было решено написать небольшой обзор с простенькими примерами. Для тех, кого тема заинтересовала, рекомендую прочитать книгу номер [3] из списка литературы (на английском языке), она написана доступным языком с большим количеством примеров.
[1] ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
[2] ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.
Для любой системы взаимно простых чисел p1, … pn, любое число X из диапазона [0; M), где M = p1*p2*…*pn взаимооднозначно представимо в виде вектора (a1, a2, …, an), где ai = X%pi (здесь и далее «%» — операция взятия остатка от целочисленного деления X на pi).
p1, … pn – модули системы
a1, a2, …, an – остатки (вычеты) числа по заданной системе модулей
На первый взгляд непонятно какое преимущество может дать такая система, однако существует 2 свойства, которые позволяют эффективно использовать модулярную арифметику в некоторых областях микроэлектроники:
- Отсутствие переноса разрядов в сложении и умножении. Пусть нам дано два числа X1 и X2, представленные в виде системы остатков (x11, x12, …, x1n) и (x21, x22, …, x2n) по системе взаимнопростых чисел (p1, p2, …, pn). В этом случае:
X3 = X1 + X2 = ((x11+x21)%p1, (x12+x22)%p2, …, (x1n+x2n)%pn)
X4 = X1 * X2 = ((x11*x21)%p1, (x12*x22)%p2, …, (x1n*x2n)%pn)
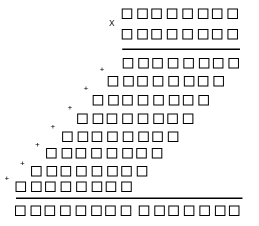
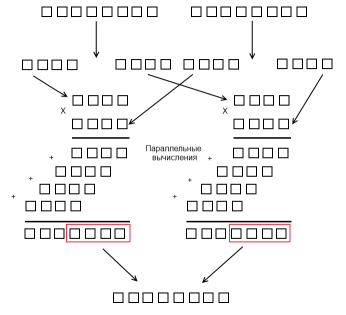
То есть что бы сложить или умножить два числа, достаточно сложить или умножить соответствующие элементы вектора, что для микроэлектроники означает, что это можно сделать параллельно и из-за малых размерностей p1, p2, …, pn сделать очень быстро. - Ошибка в одной позиции вектора не влияет на расчеты в других позициях вектора. В отличие от позиционной системы счисления все элементы вектора равнозначны и ошибка в одном из них ведет всего лишь к сокращению динамического диапазона. Этот факт позволяет проектировать устройства с повышенной отказоустойчивостью и коррекцией ошибок.
| Обычное умножение | Модулярное умножение |
 |
 |
Но не всё так гладко, как хотелось бы. В отличие от позиционной системы счисления, следующие операции (называемые «немодульными») выполняются сложнее, чем в позиционной системе счисления: сравнение чисел, контроль переполнения, деление, квадратный корень и.т.д. Первые успешные попытки применения модулярной арифметики в микроэлектронике были предприняты ещё в 1950-х годах, но из-за сложностей с немодульными операциями интерес несколько утих. Однако в настоящее время модулярная арифметика снова возвращается в микроэлектронику по следующим причинам:
- большое распространение мобильных процессоров, в которых требуется высокая скорость при маленьком потреблении энергии. Отсутствие переноса в арифметических операциях сложения/умножения позволяет снизить потребление энергии.
- увеличивающаяся плотность элементов на кристалле в некоторых случаях не позволяет провести полное тестирование, поэтому растет важность устойчивости процессоров к возможным ошибкам.
- появление специализированных процессоров с большим числом операций над векторами, которые требуют высокой скорости и включают в себя преимущественно сложение и умножение чисел (как пример умножение матриц, скалярное произведение векторов, преобразования Фурье и.т.д).
В данный момент модулярная арифметика применяется в следующих областях: цифровая обработка сигналов, криптография, обработка изображений/аудио/видео и.т.д.
Прямое преобразование
Прямое преобразование из позиционной системы счисления (обычно в двоичном виде) в систему счисления в остатках заключается в нахождении остатков от деления по каждому из модулей системы.
Пример: Пусть требуется найти представление числа X = 25 по системе модулей (3, 5, 7). X = (25%3, 25%5, 25%7) = (1, 0, 4).
Реализация нахождения вычета в микроэлектронике по заданному модулю строится на следующих свойствах вычетов:
(a+b) % p = (a%p + b%p)%p
(a*b) % p = (a%p * b%p)%p
Любое число X можно записать в виде X%p = (xn-1*2n-1 + xn-2*2n-2 + x0*20)%p = ((xn-1)%p*2n-1%p) + ((xn-2)%p*2n-2%p) + … + x0%p)%p. Поскольку в данном случае xn-1, … x0 равны 0 или 1, то фактически нам требуется сложить вычеты вида (2i%p).
Пример: пусть задано число 25 или в двоичной системе счисления 11001 и требуется найти остаток по модулю 7.
25%7 = (1*24 + 1*23 + 0*22 + 0*1 + 1*20)%7 = (24%7 + 23%7 + 1%7)%7 = (2 + 1 + 1)%7 = 4
Систему используемых модулей подбирают под конкретную задачу. Например, для представления 32-х битных чисел достаточно следующей системы модулей: (7, 11, 13, 17, 19, 23, 29, 31) – все они взаимнопросты друг с другом, их произведение равно 6685349671 > 4294967296. Каждый из модулей не превышает 5 бит, то есть операции сложения и умножения будут производиться над 5-битными числами.
Особое значение так же имеет система модулей вида: (2n-1, 2n, 2n+1) в связи с тем, что прямое и обратное преобразование для них выполняется простейшим образом. Что бы получить остаток от деления на 2n достаточно взять последние n цифр двоичного представления числа.
Арифметические операции
Пример: пусть задана система модулей (3, 5, 7), то есть мы можем выполнять операции, результат которых не превышает 3*5*7 = 105. Умножим два числа 8 и 10.
8 = (8%3, 8%5, 8%7) = (2, 3, 1)
10 = (10%3, 10%5, 10%7) = (1, 0, 3)
8*10 = ((2*1)%3, (3*0)%5, (1*3)%7) = (2, 0, 3)
Проверяем
80 = (80%3, 80%5, 80%7) = (2, 0, 3)
Обратное преобразование
Обратное преобразование из системы счисления в остаточных классах в позиционную систему счисления производится одним из двух способов:
- На базе Китайской теоремы об остатках или системы ортогональных базисов
- На базе полиадического кода (другие названия mixed-radix system, система, со смешанным основанием)
Остальные предложенные в различной литературе способы, по сути, являются смесью этих двух.
Способ, основанный на Китайской теореме об остатках, базируется на следующей идее:
X = (x1, x2, … xn) = (x1, 0, …, 0) + (0, x2, …, 0) + … + (0, 0, …., xn) = x1*(1, 0, …, 0) + x2*(0, 1, …, 0) + … + xn*(0, 0, …, 1).
То есть для обратного преобразования требуется найти систему ортогональных базисов B1 = (1, 0, …, 0), B2 = (0, 1, …, 0), …, BN = (0, 0, …, 1). Эти вектора находятся один раз для заданного базиса, а для их поиска требуется решить уравнение вида: (Mi*bi)%pi = 1, где Mi = M/pi, а bi – искомое число. В этом случае позиционное представление Bi = Mi*bi и
X = (x1*(M1*b1) + x2*(M2*b2) + … + xn*(Mn*bn))%M
Пример: пусть задана система модулей (3, 5, 7), найдем значения Mi и bi (0 < i <= 3)
M = 3*5*7 = 105
M1 = 105/3 = 35
M2 = 105/5 = 21
M3 = 105/7 = 15
(35*b1)%3 = 1 => b1 = 2
(21*b2)%5 = 1 => b2 = 1
(15*b3)%7 = 1 => b3 = 1
Теперь преобразуем какое-нибудь число в системе остаточных классов. Положим
X = (2, 3, 1) = (2*35*2 + 3*21*1 + 1*15*1)%105 = (140 + 63 + 15)%105 = 218%105 = 8
Минус этого метода заключается в том, что для обратного преобразования требуется умножение и сложение больших чисел (M1, …, Mn), а так же операция взятия остатка по модулю большого числа M.
Способ на базе полиадического кода, базируется на идее, что любое число X может быть представлено в системе взаимно простых чисел p1, … pn, как [4]:
X = a1 + a2*p1 + a3*p1*p2 +… + an-1*p1*p2*…*pn-2 + an*p1*p2*…*pn-1, где 0 < ai < pi
- X%p1 = x1 = a1
- (X – a1)%p2 = (x2 — a1)%p2 = (a2*p1)%p2 => a2 = ((p1-1)%p2*(x2 — a1))%p2
- (X — a1 — a2*p1)%p3 = (a3*p1*p2)%p3 => a3 = ((p2-1)%p3*((p1-1)%p3*(x3 — a1) — a2))%p3
- …
Для использования этого метода требуются константы вида (pi-1)%pk-1. Можно также заметить, что начинать вычисление a3 можно, как только появилось значение a1. На основе этого метода можно строить конвеерные преобразователи.
Пример: Рассмотрим тот же пример — найдем позиционное представление числа X = (2, 3, 1) в системе модулей (3, 5, 7)
- a1 = x1 = 2
- a2 = ((p1-1)%p2*(x2 — a1))%p2 = ((3-1)%5*(3 — 2))%5 = 2*1 = 2
- a3 = ((p2-1)%p3*((p1-1)%p3*(x3 — a1) — a2))%p3 = ((5-1)%7*((3-1)%7*(1 — 2) — 2))%7 = (3*(5*(1-2)-2))%7 = (3*(-7))%7 = 0
- X = a1 + a2*p1 + a3*p1*p2 = a1 + 3*a2 + 15*a3 = 2 + 3*2 + 15*0 = 8
Замечание: что бы найти константу вида (3-1)%5 требуется решить уравнение (3*x)%5 = 1, где 0 <= x < 5
P.S.
Статья написана несколько сумбурно, потому что тема достаточно большая и в одну статью вместить все не представляется возможным. В следующих статьях я попробую расписать более подробно различные аспекты модулярной арифметики. На Хабре же я не нашел вообще ничего что относится к этой теме, только краткие упоминания в других статьях, поэтому и было решено написать небольшой обзор с простенькими примерами. Для тех, кого тема заинтересовала, рекомендую прочитать книгу номер [3] из списка литературы (на английском языке), она написана доступным языком с большим количеством примеров.
Литература
[1] ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B7%D0%B8%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%81%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F
[2] ru.wikipedia.org/wiki/%D0%9A%D0%B8%D1%82%D0%B0%D0%B9%D1%81%D0%BA%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%BE%D0%B1_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%B0%D1%85
[3] Amos Omondi, Benjamin Premkumar, Residue Number Systems: Theory and Implementation, 2007.
[4] M. A. Soderstrand, W. K. Jenkins, G. A. Jullien and F. J. Taylor. 1986. Residue Number System Arithmetic: Modern Applications in Digital Signal Processing, IEEE Press, New York.