После публикации топика было получено немало интересных, полезных, и приятных комментариев. Благодаря этому, я продолжил изучение вопроса, переделал алгоритм расчета и получил некоторые любопытные факты (в том числе вероятности выигрыша при различном количестве мин), которые, я думаю, заинтересуют вас.
Совет о полном переборе заставил меня задуматься, так как первоначально я не воспринимал его всерьез, считая, что перебор займет очень большое время. Это действительно было бы так, если бы перебирались мины на всем поле. Но скачав сапер от IXBT, я понял, что это вовсе необязательно. Имеет смысл рассматривать только те клетки, которые непосредственно соседствуют с открытыми числами. На вероятность расположения мин в других клетках эти числа не влияют.
Кстати, поизучав скачанный сапер, я обнаружил, что он совершенно не учитывает при расчете оставшееся количество мин на поле. На первый взгляд это некритично, так как, к примеру, вокруг единственной «4» вероятности всегда будут 50/50. Но бывают случаи, когда неучет этого фактора ведет к очень нехорошим последствиям, например:
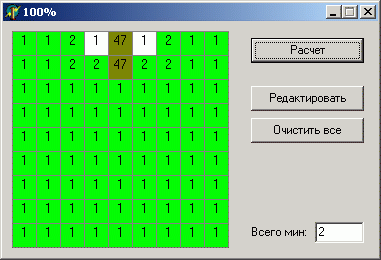
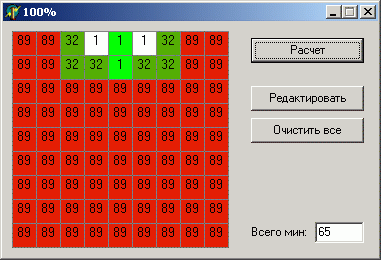
Данные абсолютно одинаковые, кроме количества мин, однако разница в результате очень показательна.
Думаю вы и сами догадываетесь почему так происходит. Можно выделить 2 способа расположения мин: одна мина между единицами (рядом больше нет) или две мины по одной на каждую единицу. Если на всем поле 2 мины, то вероятнее одна расположится между единицами, зато второй можно быть в почти любой клетке поля, нежели обе будут рядом. И наоборот, если мин очень много, то вероятность того, что в области из 6 клеток (рядом с единицами) не будет ни одной мины, невелика.
Теперь расчет от IXBT:
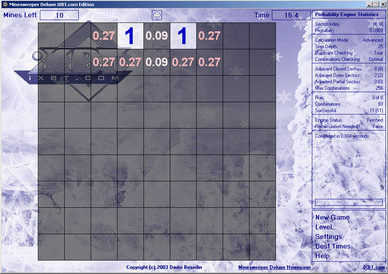
При любом количестве мин вероятности одни и те же. На основе его данных я пришел к выводу, что при переборе вариантов он подразумевает, что все они равновероятны, но, как видно из примера, это совершенно не так.
Расчет вероятности каждого случая добавил мне немного хлопот. Если в процессе перебора вариант удовлетворял условиям, то нужно было посчитать вероятность этого случая, и во все клетки с минами (гипотетическими минами, полученными только для текущего варианта) прибавлять полученное число. Хотя сам расчет сложности не представляет, используются лишь основы комбинаторики.
Было бы прекрасно закончить на этой хорошей ноте, так как все отлично перебиралось, и получаемые вероятности полностью подтверждались теоретическими расчетами и первой версией программы. Но это если количество клеток, граничащих с открытыми числами, было не очень велико. При числе свыше 23, расчет занимал более секунды, что было не очень приятно. Поэтому на вооружение был принят проверенный способ (Монте-Карло, как заметили в предыдущем топике). Случайный набор генерируется в тех же соседних клетках, что позволило повысить количество итераций с 10 тысяч до миллиона. К сожалению, в сложных случаях по прежнему выдается ошибка, но это происходит гораздо реже. А в целом работает точно и быстро. Скачать можно здесь.
Когда программа была готова, стало интересно проверить частоту выигрыша от количества мин. Игр проводилось от тысячи до миллиона, в зависимости от сложности и времени. На диаграмме приведены лишь числа от 1 до 32, так дальше вероятность становится очень маленькой. Остальное ниже.
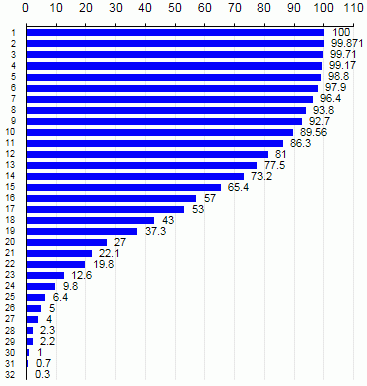
Как видно, функция является достаточно гладкой. Я попытался найти эмпирическую формулу для нее, но пока безрезультатно, поэтому будет здорово если вы подскажете.
Специально для M_org, который поинтересовался слабо ли мне пройти с 64-мя минами, прогнал 10 миллионов раз и ни разу не выиграл. Зато теперь я могу смело ответить, что не слабо даже с 79-ю :)
Совет о полном переборе заставил меня задуматься, так как первоначально я не воспринимал его всерьез, считая, что перебор займет очень большое время. Это действительно было бы так, если бы перебирались мины на всем поле. Но скачав сапер от IXBT, я понял, что это вовсе необязательно. Имеет смысл рассматривать только те клетки, которые непосредственно соседствуют с открытыми числами. На вероятность расположения мин в других клетках эти числа не влияют.
Кстати, поизучав скачанный сапер, я обнаружил, что он совершенно не учитывает при расчете оставшееся количество мин на поле. На первый взгляд это некритично, так как, к примеру, вокруг единственной «4» вероятности всегда будут 50/50. Но бывают случаи, когда неучет этого фактора ведет к очень нехорошим последствиям, например:


Данные абсолютно одинаковые, кроме количества мин, однако разница в результате очень показательна.
Думаю вы и сами догадываетесь почему так происходит. Можно выделить 2 способа расположения мин: одна мина между единицами (рядом больше нет) или две мины по одной на каждую единицу. Если на всем поле 2 мины, то вероятнее одна расположится между единицами, зато второй можно быть в почти любой клетке поля, нежели обе будут рядом. И наоборот, если мин очень много, то вероятность того, что в области из 6 клеток (рядом с единицами) не будет ни одной мины, невелика.
Теперь расчет от IXBT:

При любом количестве мин вероятности одни и те же. На основе его данных я пришел к выводу, что при переборе вариантов он подразумевает, что все они равновероятны, но, как видно из примера, это совершенно не так.
Расчет вероятности каждого случая добавил мне немного хлопот. Если в процессе перебора вариант удовлетворял условиям, то нужно было посчитать вероятность этого случая, и во все клетки с минами (гипотетическими минами, полученными только для текущего варианта) прибавлять полученное число. Хотя сам расчет сложности не представляет, используются лишь основы комбинаторики.
Было бы прекрасно закончить на этой хорошей ноте, так как все отлично перебиралось, и получаемые вероятности полностью подтверждались теоретическими расчетами и первой версией программы. Но это если количество клеток, граничащих с открытыми числами, было не очень велико. При числе свыше 23, расчет занимал более секунды, что было не очень приятно. Поэтому на вооружение был принят проверенный способ (Монте-Карло, как заметили в предыдущем топике). Случайный набор генерируется в тех же соседних клетках, что позволило повысить количество итераций с 10 тысяч до миллиона. К сожалению, в сложных случаях по прежнему выдается ошибка, но это происходит гораздо реже. А в целом работает точно и быстро. Скачать можно здесь.
Главная цель.
Когда программа была готова, стало интересно проверить частоту выигрыша от количества мин. Игр проводилось от тысячи до миллиона, в зависимости от сложности и времени. На диаграмме приведены лишь числа от 1 до 32, так дальше вероятность становится очень маленькой. Остальное ниже.

35: 17 (из 10 тыс) 0.17%
40: 10 (из 100 тыс) 0.01%
45: 3 (из 100 тыс) 0.003%
50: 6 (из млн) 0.0006%
60: 2 (из млн) 0.0002%
70: 0 (из млн) ?
75: 6 (из млн) 0.0006%
76: 32 (из млн) 0.0032%
77: 183 (из млн) 0.0183%
78: 1552 (из млн) 0.1552%
79: 25350 (из млн) 2.535%
Как видно, функция является достаточно гладкой. Я попытался найти эмпирическую формулу для нее, но пока безрезультатно, поэтому будет здорово если вы подскажете.
Специально для M_org, который поинтересовался слабо ли мне пройти с 64-мя минами, прогнал 10 миллионов раз и ни разу не выиграл. Зато теперь я могу смело ответить, что не слабо даже с 79-ю :)