kNN расшифровывается как k Nearest Neighbor или k Ближайших Соседей — это один из самых простых алгоритмов классификации, также иногда используемый в задачах регрессии. Благодаря своей простоте, он является хорошим примером, с которого можно начать знакомство с областью Machine Learning. В данной статье рассмотрен пример написания кода такого классификатора на python, а также визуализация полученных результатов.
Задача классификации в машинном обучении — это задача отнесения объекта к одному из заранее определенных классов на основании его формализованных признаков. Каждый из объектов в этой задаче представляется в виде вектора в N-мерном пространстве, каждое измерение в котором представляет собой описание одного из признаков объекта. Допустим нам нужно классифицировать мониторы: измерениями в нашем пространстве параметров будут величина диагонали в дюймах, соотношение сторон, максимальное разрешение, наличие HDMI-интерфейса, стоимость и др. Случай классификации текстов несколько сложнее, для них обычно используется матрица термин-документ (описание на machinelearning.ru).
Для обучения классификатора необходимо иметь набор объектов, для которых заранее определены классы. Это множество называется обучающей выборкой, её разметка производится вручную, с привлечением специалистов в исследуемой области. Например, в задаче Detecting Insults in Social Commentary для заранее собранных тестов комментариев человеком проставлено мнение, является ли этот комментарий оскорблением одного из участников дискуссии, само же задание является примером бинарной классификации. В задаче классификации может быть более двух классов (многоклассовая), каждый из объектов может принадлежать более чем к одному классу (пересекающаяся).
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
Примеры, приведенные ниже, реализованы на python. Для корректного их исполнения помимо python у вас должны быть установлены numpy, pylab и matplotlib. Код инициализации библиотек следующий:
Рассмотрим работу классификатора на примере. Для начала, нам нужно сгенерировать данные, на которых будут производиться эксперименты:
Для простоты я выбрал двумерное пространство, в котором случайным образом на участке от 0 до 5 по каждой из осей выбирается местоположение мат.ожидания двумерного гауссиана со среднеквадратичным отклонением 0.5. Значение 0.5 выбрано, чтобы объекты оказались достаточно хорошо разделимыми (правило трех сигм).
Чтобы посмотреть на полученную выборку, нужно выполнить следующий код:
Вот пример полученного в результате выполнения этого кода изображения:

Итак, у нас имеется набор объектов, для каждого из которых задан класс. Теперь нам нужно разбить это множество на две части: обучающую выбору и тестовую выборку. Для этого служит следующий код:
Теперь, имея обучающую выборку, можно реализовать и сам алгоритм классификации:
Для определения расстояния между объектами можно использовать не только евклидово расстояние: также применяются манхэттенское расстояние, косинусная мера, критерий корелляции Пирсона и др.
Теперь можно оценить, насколько хорошо работает наш классификатор. Для этого сгенерируем данные, разобьем их на обучающую и тестовую выборку, произведем классификацию объектов тестовой выборки и сравним реальное значение класса с полученным в результате классификации:
Для оценки качества работы классификатора используются различные алгоритмы и различные меры, более подробно можно почитать здесь: wiki
Теперь осталось самое интересное: показать работу классификатора графически. В приведенных ниже картинках я использовал 3 класса, в каждом по 40 элементов, значение k для алгоритма взял равным трем.
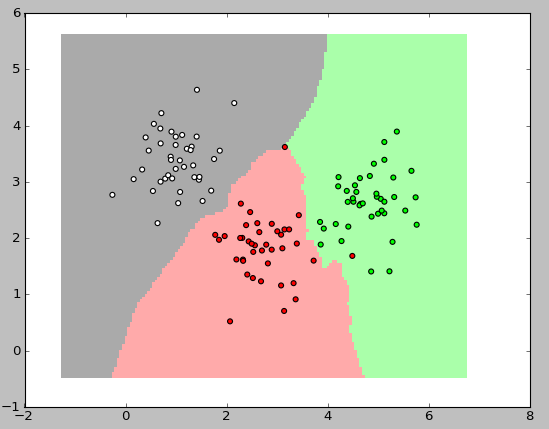

Для вывода этих картинок использован следующий код:
kNN — один из простейших алгоритмов классификации, поэтому на реальных задачах он зачастую оказывается неэффективным. Помимо точности классификации, проблемой этого классификатора является скорость классификации: если в обучающей выборке N объектов, в тестовой выборе M объектов, а размерность пространства — K, то количество операций для классификации тестовой выборки может быть оценено как O(K*M*N). И тем не менее, алгоритм работы kNN является хорошим примером для начала знакомства с Machine Learning.
1. Метод ближайших соседей на Machinelearning.ru
2. Векторная модель на Machinelearning.ru
3. Книга по Information Retrieval
4. Описание метода ближайших соседей в рамках scikit-learn
5. Книга «Программируем коллективный разум»
Задача классификации в машинном обучении — это задача отнесения объекта к одному из заранее определенных классов на основании его формализованных признаков. Каждый из объектов в этой задаче представляется в виде вектора в N-мерном пространстве, каждое измерение в котором представляет собой описание одного из признаков объекта. Допустим нам нужно классифицировать мониторы: измерениями в нашем пространстве параметров будут величина диагонали в дюймах, соотношение сторон, максимальное разрешение, наличие HDMI-интерфейса, стоимость и др. Случай классификации текстов несколько сложнее, для них обычно используется матрица термин-документ (описание на machinelearning.ru).
Для обучения классификатора необходимо иметь набор объектов, для которых заранее определены классы. Это множество называется обучающей выборкой, её разметка производится вручную, с привлечением специалистов в исследуемой области. Например, в задаче Detecting Insults in Social Commentary для заранее собранных тестов комментариев человеком проставлено мнение, является ли этот комментарий оскорблением одного из участников дискуссии, само же задание является примером бинарной классификации. В задаче классификации может быть более двух классов (многоклассовая), каждый из объектов может принадлежать более чем к одному классу (пересекающаяся).
Алгоритм
Для классификации каждого из объектов тестовой выборки необходимо последовательно выполнить следующие операции:
- Вычислить расстояние до каждого из объектов обучающей выборки
- Отобрать k объектов обучающей выборки, расстояние до которых минимально
- Класс классифицируемого объекта — это класс, наиболее часто встречающийся среди k ближайших соседей
Примеры, приведенные ниже, реализованы на python. Для корректного их исполнения помимо python у вас должны быть установлены numpy, pylab и matplotlib. Код инициализации библиотек следующий:
import random
import math
import pylab as pl
import numpy as np
from matplotlib.colors import ListedColormap
Исходные данные
Рассмотрим работу классификатора на примере. Для начала, нам нужно сгенерировать данные, на которых будут производиться эксперименты:
#Train data generator
def generateData (numberOfClassEl, numberOfClasses):
data = []
for classNum in range(numberOfClasses):
#Choose random center of 2-dimensional gaussian
centerX, centerY = random.random()*5.0, random.random()*5.0
#Choose numberOfClassEl random nodes with RMS=0.5
for rowNum in range(numberOfClassEl):
data.append([ [random.gauss(centerX,0.5), random.gauss(centerY,0.5)], classNum])
return data
Для простоты я выбрал двумерное пространство, в котором случайным образом на участке от 0 до 5 по каждой из осей выбирается местоположение мат.ожидания двумерного гауссиана со среднеквадратичным отклонением 0.5. Значение 0.5 выбрано, чтобы объекты оказались достаточно хорошо разделимыми (правило трех сигм).
Чтобы посмотреть на полученную выборку, нужно выполнить следующий код:
def showData (nClasses, nItemsInClass):
trainData = generateData (nItemsInClass, nClasses)
classColormap = ListedColormap(['#FF0000', '#00FF00', '#FFFFFF'])
pl.scatter([trainData[i][0][0] for i in range(len(trainData))],
[trainData[i][0][1] for i in range(len(trainData))],
c=[trainData[i][1] for i in range(len(trainData))],
cmap=classColormap)
pl.show()
showData (3, 40)
Вот пример полученного в результате выполнения этого кода изображения:

Получение обучающей и тестовой выборки
Итак, у нас имеется набор объектов, для каждого из которых задан класс. Теперь нам нужно разбить это множество на две части: обучающую выбору и тестовую выборку. Для этого служит следующий код:
#Separate N data elements in two parts:
# test data with N*testPercent elements
# train_data with N*(1.0 - testPercent) elements
def splitTrainTest (data, testPercent):
trainData = []
testData = []
for row in data:
if random.random() < testPercent:
testData.append(row)
else:
trainData.append(row)
return trainData, testData
Реализация классификатора
Теперь, имея обучающую выборку, можно реализовать и сам алгоритм классификации:
#Main classification procedure
def classifyKNN (trainData, testData, k, numberOfClasses):
#Euclidean distance between 2-dimensional point
def dist (a, b):
return math.sqrt((a[0] - b[0])**2 + (a[1] - b[1])**2)
testLabels = []
for testPoint in testData:
#Claculate distances between test point and all of the train points
testDist = [ [dist(testPoint, trainData[i][0]), trainData[i][1]] for i in range(len(trainData))]
#How many points of each class among nearest K
stat = [0 for i in range(numberOfClasses)]
for d in sorted(testDist)[0:k]:
stat[d[1]] += 1
#Assign a class with the most number of occurences among K nearest neighbours
testLabels.append( sorted(zip(stat, range(numberOfClasses)), reverse=True)[0][1] )
return testLabels
Для определения расстояния между объектами можно использовать не только евклидово расстояние: также применяются манхэттенское расстояние, косинусная мера, критерий корелляции Пирсона и др.
Примеры выполнения
Теперь можно оценить, насколько хорошо работает наш классификатор. Для этого сгенерируем данные, разобьем их на обучающую и тестовую выборку, произведем классификацию объектов тестовой выборки и сравним реальное значение класса с полученным в результате классификации:
#Calculate classification accuracy
def calculateAccuracy (nClasses, nItemsInClass, k, testPercent):
data = generateData (nItemsInClass, nClasses)
trainData, testDataWithLabels = splitTrainTest (data, testPercent)
testData = [testDataWithLabels[i][0] for i in range(len(testDataWithLabels))]
testDataLabels = classifyKNN (trainData, testData, k, nClasses)
print "Accuracy: ", sum([int(testDataLabels[i]==testDataWithLabels[i][1]) for i in range(len(testDataWithLabels))]) / float(len(testDataWithLabels))
Для оценки качества работы классификатора используются различные алгоритмы и различные меры, более подробно можно почитать здесь: wiki
Теперь осталось самое интересное: показать работу классификатора графически. В приведенных ниже картинках я использовал 3 класса, в каждом по 40 элементов, значение k для алгоритма взял равным трем.


Для вывода этих картинок использован следующий код:
#Visualize classification regions
def showDataOnMesh (nClasses, nItemsInClass, k):
#Generate a mesh of nodes that covers all train cases
def generateTestMesh (trainData):
x_min = min( [trainData[i][0][0] for i in range(len(trainData))] ) - 1.0
x_max = max( [trainData[i][0][0] for i in range(len(trainData))] ) + 1.0
y_min = min( [trainData[i][0][1] for i in range(len(trainData))] ) - 1.0
y_max = max( [trainData[i][0][1] for i in range(len(trainData))] ) + 1.0
h = 0.05
testX, testY = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
return [testX, testY]
trainData = generateData (nItemsInClass, nClasses)
testMesh = generateTestMesh (trainData)
testMeshLabels = classifyKNN (trainData, zip(testMesh[0].ravel(), testMesh[1].ravel()), k, nClasses)
classColormap = ListedColormap(['#FF0000', '#00FF00', '#FFFFFF'])
testColormap = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAAA'])
pl.pcolormesh(testMesh[0],
testMesh[1],
np.asarray(testMeshLabels).reshape(testMesh[0].shape),
cmap=testColormap)
pl.scatter([trainData[i][0][0] for i in range(len(trainData))],
[trainData[i][0][1] for i in range(len(trainData))],
c=[trainData[i][1] for i in range(len(trainData))],
cmap=classColormap)
pl.show()
Заключение
kNN — один из простейших алгоритмов классификации, поэтому на реальных задачах он зачастую оказывается неэффективным. Помимо точности классификации, проблемой этого классификатора является скорость классификации: если в обучающей выборке N объектов, в тестовой выборе M объектов, а размерность пространства — K, то количество операций для классификации тестовой выборки может быть оценено как O(K*M*N). И тем не менее, алгоритм работы kNN является хорошим примером для начала знакомства с Machine Learning.
Список литературы
1. Метод ближайших соседей на Machinelearning.ru
2. Векторная модель на Machinelearning.ru
3. Книга по Information Retrieval
4. Описание метода ближайших соседей в рамках scikit-learn
5. Книга «Программируем коллективный разум»