 Мне со школьных времен был интересен алгоритм вывода аналитических производных и упрощения выражений. Данная задача была актуальна впоследствии и в вузе. Тогда-то я реализовал ее, только получилось все не так, как хотелось: вместо кода IL у меня просто генерировался C# код в текстовом виде, сборки не выгружались, ну и к тому же не было возможности вывода производных в аналитическом виде. Однако потом я решил все-таки реализовать такую библиотеку, так как интерес остался. Стоит отметить, что таких библиотек в интернете большое количество, но нигде я не нашел именно этапа компиляции выражений в IL код, т.е. по сути везде выполняется интерпретация, которая не столь эффективна, в отличие от компиляции. Ну и к тому же я это разрабатывал чисто для себя, для изучения новых технологий, особо не надеясь, что результат моих трудов может где-нибудь потребоваться. Для нетерпеливых: исходники, программа.
Мне со школьных времен был интересен алгоритм вывода аналитических производных и упрощения выражений. Данная задача была актуальна впоследствии и в вузе. Тогда-то я реализовал ее, только получилось все не так, как хотелось: вместо кода IL у меня просто генерировался C# код в текстовом виде, сборки не выгружались, ну и к тому же не было возможности вывода производных в аналитическом виде. Однако потом я решил все-таки реализовать такую библиотеку, так как интерес остался. Стоит отметить, что таких библиотек в интернете большое количество, но нигде я не нашел именно этапа компиляции выражений в IL код, т.е. по сути везде выполняется интерпретация, которая не столь эффективна, в отличие от компиляции. Ну и к тому же я это разрабатывал чисто для себя, для изучения новых технологий, особо не надеясь, что результат моих трудов может где-нибудь потребоваться. Для нетерпеливых: исходники, программа.Используемые программы и библиотеки
- GOLD Parsing System — IDE для написания грамматик и генерации кода лексеров и парсеров под различные языки (C, C#, Java, JavaScript, Objective-C, Perl, Python, Ruby и др.). Основана на LALR парсинге.
- Visual Studio 2010
- GOLD.Engine — сборка под .NET, подключаемая для взаимодействия со сгенерированными таблицами.
- NUnit — Открытая среда юнит-тестирования приложений для .NET.
- ILSpy — OpenSource дизассемблер под .NET.
Этапы, на которые я разбил весь процесс:
- Построение дерева выражения
- Вычисление аналитической производной
- Упрощение (симплификация) выражения
- Обработка рациональных дробей
- Компиляция выражения
Построение дерева выражения
Парсер-генератор GOLD я выбрал, поскольку уже имею опыт с ANTLR и захотелось чего-то нового. Ну а его преимущества, по сравнению с остальными, вы можете увидеть в данной таблице. Как видим, если сравнивать с ANTLR, то GOLD основан на алгоритме LALR, а не LL. А это значит, что в теории, сгенерированный парсер быстрее и мощнее, но с другой стороны, его нельзя отлаживать (в GOLD вообще подгружается файл в бинарном формате), а если бы и можно было бы, то это было бы совсем не очевидно и неудобно. Другим большим отличием является форма задания грамматики: BNF, а не EBNF. А это означает, что грамматика, записанная в данной форме, имеет немного больший размер из-за угловых скобок, знака определения и отсутствия условных вхождений и повторений (подробней в wiki. И, например, такое правило в EBNF, как
ExpressionList = Expression { ',' Expression }
будет переписано в такой форме:
<ExpressionList> ::= <ExpressionList> ',' <Expression> | <Expression>
Итак, окончательная грамматика математических выражений имеет следующий вид:
Грамматика математических выражений
"Name" = 'Mathematics expressions'
"Author" = 'Ivan Kochurkin'
"Version" = '1.0'
"About" = ''
"Case Sensitive" = False
"Start Symbol" = <Statements>
Id = {Letter}{AlphaNumeric}*
Number1 = {Digit}+('.'{Digit}*('('{Digit}*')')?)?
Number2 = '.'{Digit}*('('{Digit}*')')?
AddLiteral = '+' | '-'
MultLiteral = '*' | '/'
<Statements> ::= <Statements> <Devider> <Statement>
| <Statements> <Devider>
| <Statement>
<Devider> ::= ';' | '.'
<Statement> ::= <Expression> '=' <Expression>
| <Expression>
<Expression> ::= <FuncDef>
| <Addition>
<FuncDef> ::= Id '(' <ExpressionList> ')'
| Id '' '(' <ExpressionList> ')'
| Id '(' <ExpressionList> ')' ''
<ExpressionList> ::= <ExpressionList> ',' <Expression>
| <Expression>
<Addition> ::= <Addition> AddLiteral <Multiplication>
| <Addition> AddLiteral <FuncDef>
| <FuncDef> AddLiteral <Multiplication>
| <FuncDef> AddLiteral <FuncDef>
| <Multiplication>
<Multiplication> ::= <Multiplication> MultLiteral <Exponentiation>
| <Multiplication> MultLiteral <FuncDef>
| <FuncDef> MultLiteral <Exponentiation>
| <FuncDef> MultLiteral <FuncDef>
| <Exponentiation>
<Exponentiation> ::= <Exponentiation> '^' <Negation>
| <Exponentiation> '^' <FuncDef>
| <FuncDef> '^' <Negation>
| <FuncDef> '^' <FuncDef>
| <Negation>
<Negation> ::= AddLiteral <Value>
| AddLiteral <FuncDef>
| <Value>
<Value> ::= Id
| Number1
| Number2
| '(' <Expression> ')'
| '|' <Expression> '|'
| '(' <Expression> ')' ''
| '|' <Expression> '|' ''
| Id ''
В грамматике вроде бы все очевидно, за исключением лексемы: Number1 = {Digit}+('.'{Digit}*('('{Digit}*')')?)? Данная конструкция позволяет парсить строки следующего вида: 0.1234(56), что означает рациональную дробь: 61111/495000. Про преобразование такой строки в дробь я расскажу позже.
Итак, после того как скомпилированные грамматические таблицы (Compiled Grammar Table File) сгенерированы, и создан каркас класса парсера, необходимо модифицировать последний для того, чтобы строилось подходящее AST дерево. Каркас класса парсера в данном случае это .cs файл, в котором написан цикл обхода по всем всем правилам грамматики, обработка исключений в случае неверной последовательности лексем и других ошибок (кстати говоря в GOLD есть тоже разные генераторы таких каркасов, и я выбрал Cook .NET). Итак, в нашем случае «подходящее» обозначает дерево, состоящее из узлов, которые могут иметь типы:
- Calculated — узел, представляющий рассчитанную константу в приемлемом для компилятора формате double, например «0.714285714285714», «0.122222222222222». Для каждой такой константы создается новый объект, даже если они одинаковые.
- Value — узел, представляющий рассчитанную константу в формате рациональной дроби, т.е. 1 представляется как «1/1», «0.1(2)» — как «11/90», «0.1234» — как «617/5000». Для каждой такой константы создается новый объект, даже если они одинаковые.
- Constant — узел, представляющий неопределенную константу, например «a», «b» и др. Если в выражении встречаются две таких константы, то они указывают на один узел.
- Variable — узел, представляющий переменную, например «x», «y» и др. Если в выражении определенная переменная встречается несколько раз, то для нее создается только один объект, так же как и для неопределенной константы. Важно понимать, что разграничение константы и переменной важно только на этапе вывода аналитическое производной, а в других случаях это знание не обязательно.
- Function — узел, представляющий функцию, например "+", «sin», "^" и другие. Единственный узел, который может иметь потомков.
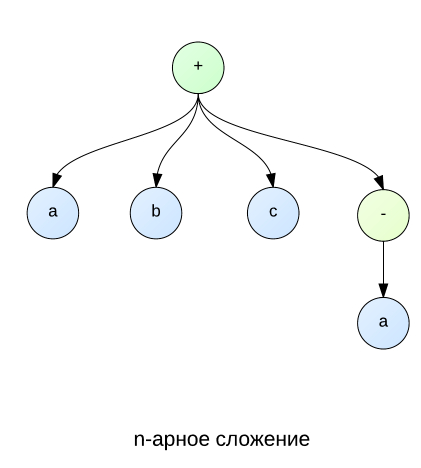
Все типы узлов наглядно представлены на рисунке:

Из грамматики видно, что узлы полученного дерева либо не имеют детей (например, значения или переменные), либо имеют от одного до двух детей в случае стандартных функций (например, cos, сложение, возведение в степень). Все остальные функции могут иметь бОльшее количество аргументов, но они не рассматривались.
Таким образом, все узлы (а точнее узлы с функциями) имеют от 0 до 2 детей включительно. Это верно с теоретической точки зрения. Но на самом деле пришлось сделать так, чтобы функции "+" и "*" имели неограниченное количество детей для того, чтобы облегчить задачу симплификации, которая будет рассмотрена позже. Кстати, от таких бинарных операций, как "-" и "/" тоже пришлось отказаться по таким же причинам (они были заменены на сложение с отрицанием правой части и умножением с обращением правой части).
Итак, на этапе разбора все узлы для каждого правила попадают или извлекаются из буфера, который называется Nodes. Таким образом, в конце всего процесса в этом буфере остается одна или несколько функций с правой и левой частью. Также в процессе парсинга для того, чтобы функции сложения и умножения сразу создавались мультинарными, использовались дополнительные буферы ArgsCount и ArgsFuncTypes, хранящие текущее количество аргументов в функции и тип текущей функции соответственно. Таким образом, например для функции умножения, используется данный код:
Обработка первого множителя:
// <Multiplication> ::= <Exponentiation>
if (MultiplicationMultiChilds)
PushFunc(KnownMathFunctionType.Mult);
Обработка i-того множителя:
// <Multiplication> ::= <Multiplication> MultLiteral <Exponentiation>
// <Multiplication> ::= <Multiplication> MultLiteral <FuncDef>
if (KnownMathFunction.BinaryNamesFuncs[r[1].Data.ToString()] == KnownMathFunctionType.Div)
Nodes.Push(new FuncNode(KnownMathFunctionType.Exp, new MathFuncNode[] { Nodes.Pop(), new ValueNode(-1) }));
ArgsCount[ArgsCount.Count - 1]++;
Обработка последнего множителя:
// <Addition> ::= <Multiplication>
if (MultiplicationMultiChilds)
PushOrRemoveFunc(KnownMathFunctionType.Mult);
if (AdditionMultiChilds)
PushFunc(KnownMathFunctionType.Add);
Из этого кода видно, что, например, если никакого умножения и нет, то последнюю функции умножения с нулевым количеством элементов нужно удалить с помощью PushOrRemoveFunc. Аналогичные действия нужно провести и для сложения.
Обработка функций одного аргумента, бинарных функций, констант, переменных и значений является тривиальной, и это все можно посмотреть в MathExprParser.cs.
Вычисление аналитической производной
На данном этапе нужно преобразовать функцию в ее производную.
Как известно из первого этапа, в созданном дереве выражения существуют только четыре типа узлов (пятый появляется позже). Для них и определим производную:
- Value' = 0
- Constant' = 0
- Variable' = 1
- Function' = Derivatives[Function]
Поясню: для производной функции нужно взять заранее подготовленное табличное значение, и это вызывает определенные трудности, потому что внутри этого значения тоже есть производные, т.е. процесс имеет рекурсивный характер. Полный же список таких реализованных подстановок вы можете увидеть под спойлером ниже.
Список производных
(f(x) ^ g(x))' = f(x) ^ g(x) * (f(x)' * g(x) / f(x) + g(x)' * ln(f(x)));");
neg(f(x))' = neg(f(x)');");
sin(f(x))' = cos(f(x)) * f(x)';
cos(f(x))' = -sin(f(x)) * f(x)';
tan(f(x))' = f(x)' / cos(f(x)) ^ 2;
cot(f(x))' = -f(x)' / sin(f(x)) ^ 2;
arcsin(f(x))' = f(x)' / sqrt(1 - f(x) ^ 2);
arccos(f(x))' = -f(x)' / sqrt(1 - f(x) ^ 2);
arctan(f(x))' = f(x)' / (1 + f(x) ^ 2);
arccot(f(x))' = -f(x)' / (1 + f(x) ^ 2);
sinh(f(x))' = f(x)' * cosh(x);
cosh(f(x))' = f(x)' * sinh(x);
arcsinh(f(x))' = f(x)' / sqrt(f(x) ^ 2 + 1);
arcosh(f(x))' = f(x)' / sqrt(f(x) ^ 2 - 1);
ln(f(x))' = f(x)' / f(x);
log(f(x), g(x))' = g'(x)/(g(x)*ln(f(x))) - (f'(x)*ln(g(x)))/(f(x)*ln(f(x))^2);
Стоит отметить, что все производные не записано жестко в коде, а тоже могут вводиться и парситься динамически.
В этом списке нет сложения и умножения потому что, как упоминалось выше, это функции с несколькими аргументами. А для того, чтобы парсить такие правила, необходимо было бы еще написать много кода. По этим же причинам, здесь нет композиции функций, т.е. (f(g(x)))' = f(g(x))' * g(x)', а вместо этого все функции представлены как композиции функций.
Также, если для функции не найдена подстановка в Derivatives (т.е. неопределенная функция), то она просто заменяется на функцию со штрихом: т.е. f(x) превратится в f(x)'.
После того, как аналитическая производная успешно была получена, возникает проблема, которая заключается в том, что в получившееся выражении возникает очень много «мусора», такого как a + 0, a * 1, a * a^-1 и пр., а также получившееся выражение можно вычислить более оптимальным образом. Например, даже для простого выражения получится некрасивое выражение:
(x^2 + 2)' = 0 + 2 * 1 * x ^ 1
Для устранения таких таких недостатков используется упрощение.
Упрощение (симплификация) выражения
На этом этапе, в отличие от этапа вычисления производных, я не стал записывать правила симплификации в отдельном месте, для их последующего его разбора из-за того, что функции сложения и умножения являются функциями нескольких аргументов, что представляет определенную сложность в создании таких правил в контексте итеративного языка.
В начале топика я затронул тему про то, почему сложение и умножение представлено в виде n-арных функций. Представим ситуацию, изображенную на картинке ниже. Здесь видим, что a и -a сокращаются. Но как это сделать в случае бинарных функций? Для этого нужно перебирать узлы a, b и c, чтобы потом обнаружить, что a и -a являются детьми одного узла, а значит их можно сократить вместе с узлом. Но, понятное дело, что перебор деревьев это не такая простая задача, так как куда проще производить все действия в цикле сразу со всеми детьми, как это представлено на рисунке справа. Кстати, такой перебор нам позволяют сделать математические свойства ассоциативности и коммутативности.
 |
 |
Во время процесса симплификации возникает задача сравнения двух узлов, которые, в свою очередь, могут иметь один из четырех типов. Это нужно, например, для того, чтобы сократить такие выражения как sin(x + y) и -sin(x + y). Понятно, что можно по узлам сравнить сами узлы и все их потомки. Но проблема заключается в том, что данный метод не справится с ситуацией, когда слагаемые или множители переставлены местами, например sin(x + y) и -sin(y + x). Для разрешения данной проблемы используется предварительная сортировка слагаемых или множителей, для которых выполняется свойство коммутативности (т.е. для сложения и вычитания). Сравниваются узлы так, как показано на картинке ниже, т.е. значения меньше констант, константы меньше переменных и т.д. Для функций все немного сложнее, поскольку нужно сравнить не только их названия, но и количество аргументов и сами аргументы.

Таким образом, после всех вышеописанных преобразований и переборов, исходное выражение неплохо упрощается.
Обработка рациональных дробей
В найденных мною реализациях рациональных не было конвертации обычного строкового типа, например 0.666666, в тип дроби с определенным числителем и знаменателем, т.е. в 2 / 3 с определенной точностью. Тогда я решил все-таки написать свою реализацию с большим количеством опций. Функции ниже могут, например, определить, является ли какое-то число чисто иррациональным, или оно имеет период или конечную дробную часть и может быть преобразовано в рациональное, например sin(pi) в 0 при определенной точности. А вообще другие подробности смотрите в моем ответе на stackoverflow.com. Краткое графическое пояснения метода представлено на рисунке ниже, а код — в листинге ниже. Стоит отметить, что все-таки точности стандартных математических функций и типа double не хватает для нормального распознавания рациональных и вещественных чисел, однако теоретически все работает.

Преобразование decimal в дробь
/// <summary>
/// Convert decimal to fraction
/// </summary>
/// <param name="value">decimal value to convert</param>
/// <param name="result">result fraction if conversation is succsess</param>
/// <param name="decimalPlaces">precision of considereation frac part of value</param>
/// <param name="trimZeroes">trim zeroes on the right part of the value or not</param>
/// <param name="minPeriodRepeat">minimum period repeating</param>
/// <param name="digitsForReal">precision for determination value to real if period has not been founded</param>
/// <returns></returns>
public static bool FromDecimal(decimal value, out Rational<T> result,
int decimalPlaces = 28, bool trimZeroes = false, decimal minPeriodRepeat = 2, int digitsForReal = 9)
{
var valueStr = value.ToString("0.0000000000000000000000000000", CultureInfo.InvariantCulture);
var strs = valueStr.Split('.');
long intPart = long.Parse(strs[0]);
string fracPartTrimEnd = strs[1].TrimEnd(new char[] { '0' });
string fracPart;
if (trimZeroes)
{
fracPart = fracPartTrimEnd;
decimalPlaces = Math.Min(decimalPlaces, fracPart.Length);
}
else
fracPart = strs[1];
result = new Rational<T>();
try
{
string periodPart;
bool periodFound = false;
int i;
for (i = 0; i < fracPart.Length; i++)
{
if (fracPart[i] == '0' && i != 0)
continue;
for (int j = i + 1; j < fracPart.Length; j++)
{
periodPart = fracPart.Substring(i, j - i);
periodFound = true;
decimal periodRepeat = 1;
decimal periodStep = 1.0m / periodPart.Length;
var upperBound = Math.Min(fracPart.Length, decimalPlaces);
int k;
for (k = i + periodPart.Length; k < upperBound; k += 1)
{
if (periodPart[(k - i) % periodPart.Length] != fracPart[k])
{
periodFound = false;
break;
}
periodRepeat += periodStep;
}
if (!periodFound && upperBound - k <= periodPart.Length && periodPart[(upperBound - i) % periodPart.Length] > '5')
{
var ind = (k - i) % periodPart.Length;
var regroupedPeriod = (periodPart.Substring(ind) + periodPart.Remove(ind)).Substring(0, upperBound - k);
ulong periodTailPlusOne = ulong.Parse(regroupedPeriod) + 1;
ulong fracTail = ulong.Parse(fracPart.Substring(k, regroupedPeriod.Length));
if (periodTailPlusOne == fracTail)
periodFound = true;
}
if (periodFound && periodRepeat >= minPeriodRepeat)
{
result = FromDecimal(strs[0], fracPart.Substring(0, i), periodPart);
break;
}
else
periodFound = false;
}
if (periodFound)
break;
}
if (!periodFound)
{
if (fracPartTrimEnd.Length >= digitsForReal)
return false;
else
{
result = new Rational<T>(long.Parse(strs[0]), 1, false);
if (fracPartTrimEnd.Length != 0)
result = new Rational<T>(ulong.Parse(fracPartTrimEnd), TenInPower(fracPartTrimEnd.Length));
return true;
}
}
return true;
}
catch
{
return false;
}
}
public static Rational<T> FromDecimal(string intPart, string fracPart, string periodPart)
{
Rational<T> firstFracPart;
if (fracPart != null && fracPart.Length != 0)
{
ulong denominator = TenInPower(fracPart.Length);
firstFracPart = new Rational<T>(ulong.Parse(fracPart), denominator);
}
else
firstFracPart = new Rational<T>(0, 1, false);
Rational<T> secondFracPart;
if (periodPart != null && periodPart.Length != 0)
secondFracPart =
new Rational<T>(ulong.Parse(periodPart), TenInPower(fracPart.Length)) *
new Rational<T>(1, Nines((ulong)periodPart.Length), false);
else
secondFracPart = new Rational<T>(0, 1, false);
var result = firstFracPart + secondFracPart;
if (intPart != null && intPart.Length != 0)
{
long intPartLong = long.Parse(intPart);
result = new Rational<T>(intPartLong, 1, false) + (intPartLong == 0 ? 1 : Math.Sign(intPartLong)) * result;
}
return result;
}
private static ulong TenInPower(int power)
{
ulong result = 1;
for (int l = 0; l < power; l++)
result *= 10;
return result;
}
private static decimal TenInNegPower(int power)
{
decimal result = 1;
for (int l = 0; l > power; l--)
result /= 10.0m;
return result;
}
private static ulong Nines(ulong power)
{
ulong result = 9;
if (power >= 0)
for (ulong l = 0; l < power - 1; l++)
result = result * 10 + 9;
return result;
}
Компиляция выражения
Для преобразования полученного семантического дерева в код IL после этапа симплификации, я использовал Mono.Cecil.
В начале процесса создается сборка, класс и метод, в который будут записываться команды. Потом для каждого FuncNode рассчитывается, сколько он раз встречается в программе. Например, если есть функция sin(x^2) * cos(x^2), то в ней функция возведения x в степень 2 встречается два раза, а функции sin и cos — по одному. В дальнейшем, данная информация о повторах вычислений функций используется следующим образом (т.е. таким образом второго раза вычисления одной и той же функции не происходит):
if (!func.Calculated)
{
EmitFunc(funcNode);
func.Calculated = true;
}
else
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
После генерации всего этого кода, возможны еще некоторые оптимизации IL кода, представленные на рисунке ниже.
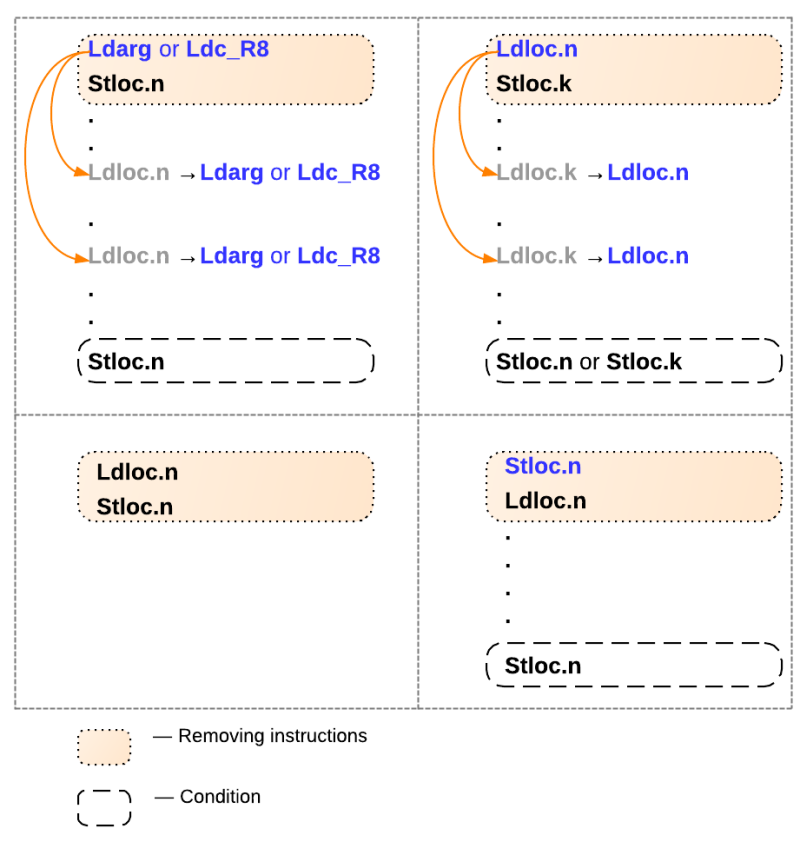
На данном рисунке:
- Ldarg — Операция загрузки определенного аргумента функции в стек.
- Ldc_R8 — Загрузка определенного значения double в стек.
- Stloc.n — Извлечение из стека последнего значения и его сохранение в локальную переменную n.
- Ldloc.n — Помещение локальной переменной n в стек.
Инструкции в бежевых прямоугольниках можно удалить, если выполнены определенные условия. Например, случай на левом верхнем изображении описывается так: Если текущая инструкция — это загрузка аргумента из функции или загрузка константы, и следующая инструкция — ее сохранение в локальную переменную n, то данный блок инструкций можно удалить, предварительно заменив инструкции загрузки локальной переменной n на загрузку аргумента функции или загрузки константы. Процесс замены продолжать до первой инструкции сохранения в локальную переменную n. Аналогичным образом объясняются остальные три случая. например последовательность Ldloc.n; Stloc.n сразу может быть удалена.
Стоит отметить, что данные оптимизации применимы в случае отсутствия ветвления в коде, и это очевидно почему (если не совсем очевидно, то предлагаю поразмыслить). Но так как код математических функций и их производных не может содержать циклов в моем случае, то это все работает.
Быстрое возведение в степень
Я думаю, что почти все знают про алгоритм быстрого возведения числа в степень. Но ниже представлен данный алгоритм на уровне компиляции:
Алгоритм быстрого возведения в степень, реализованный в IL коде
if (power <= 3)
{
IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
for (int i = 1; i < power; i++)
{
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Mul));
}
}
else if (power == 4)
{
IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Mul));
IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number));
IlInstructions.Add(new OpCodeArg(OpCodes.Mul));
}
else
{
// result: funcNode.Number
// x: funcNode.Number + 1
//int result = x;
IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1));
power--;
do
{
if ((power & 1) == 1)
{
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1));
IlInstructions.Add(new OpCodeArg(OpCodes.Mul));
}
if (power <= 1)
break;
//x = x * x;
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1));
IlInstructions.Add(new OpCodeArg(OpCodes.Ldloc, funcNode.Number + 1));
IlInstructions.Add(new OpCodeArg(OpCodes.Mul));
IlInstructions.Add(new OpCodeArg(OpCodes.Stloc, funcNode.Number + 1));
power = power >> 1;
}
while (power != 0);
}
Стоит отметить, что алгоритм быстрого возведения в степень не является самым оптимальным алгоритмом возведения в степень. Например, ниже представлено перемножение одинаковых переменных пять раз двумя способами. Оптимизации типа x^4 + x^3 + x^2 + x = x*(x*(x*(x + 1) + 1) + 1) тоже у меня не реализованы.
- var t = a ^ 2; a*a*a*a*a*a = t ^ 2 * t — обычный «быстрый» алгоритм.
- a*a*a*a*a*a = (a ^ 3) ^ 2 — оптимальный «быстрый» алгоритм.
Кстати, еще стоит упомянуть, что для обычных фиксированных чисел double, результат перемножения для упомянутых выше перемножений в разном порядке, будет различный (т.е. (a ^ 2) ^ 2 * a ^ 2 != (a ^ 3) ^ 2). И из-за этого некоторые компиляторы не оптимизируют многие подобные выражения. По этому поводу есть интересные Q&A в stackoverlofw: Why doesn't GCC optimize a*a*a*a*a*a to (a*a*a)*(a*a*a)? и Why Math.Pow(x, 2) not optimized to x * x neither compiler nor JIT?.
Оптимизация локальных переменных
Как известно из предыдущих этапов, локальные переменные используются для хранения результата всех функций, которые встречаются в исходном выражении более 1 раза. Для работы с локальными переменными используются всего две простые инструкции: stloc и ldloc, которые используют один аргумент, отвечающий за номер данной локальной переменной. Но если номер локальной переменной инкрементировать каждый раз при появлении повторяющегося результата вычислений (для ее создания), то локальных переменных может быть очень много. Для нивелирования данной проблемы, был реализован алгоритм сжатия жизненных циклов локальных переменных, процесс которого можно наглядно увидеть на рисунке ниже. Как видим, вместо 5 локальных переменных в выражении можно использовать всего 3. Однако этот «жадный» алгоритм не является самым оптимальным перестановки, однако он вполне подходит к реализуемой задаче.
 |
 |
Компиляция неопределенных функций и их производных
В разработанной библиотеке можно использовать не только простые функции от одного переменного вида f(x), но и другие, такие как f(x,a,b(x)), где a — неизвестная константа, а b(x) — неизвестная функция, передаваемая в виде делегата. Как известно, определение производной от любой функции выглядит следующим образом: b(x)' = (b(x + dx) — b(x)) / dx. И когда модуль компиляции встречает неопределенную функцию, он генерирует следующий код:
ldarg.1
ldarg.0
callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T)
ret
Код вычисления производной неопределенной функции (dx = 0.000001)
ldarg.1
ldarg.0
ldc.r8 1E-06
add
callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T)
ldarg.1
ldarg.0
callvirt TResult System.Func`2<System.Double,System.Double>::Invoke(T)
sub
ldc.r8 0.000001
div
ret
Для численного вычисления производных, можно использовать и другие, более точные методы.
Тестирование
Тестирование проводилось для нескольких этапов обработки, которые можно посмотреть в проекте MathFunction.Tests. Из интересных моментов можно упомянуть использование WolframAlpha.NET для тестирования аналитических производных и загрузку и выгрузку сборок с помощью доменов.
WolframAlpha
WolframAlpha.NET — это API оболочка известного математического сервиса wolframalpha. В моем проекте она пригодилась для того, чтобы сверять заведомо правильную производную, полученную на этом сервисе, с производной, полученной с помощью моей библиотеки. Использовалось следующим образом:
public static bool CheckDerivative(string expression, string derivative)
{
return CheckEquality("diff(" + expression + ")", derivative);
}
public static bool CheckEquality(string expression1, string expression2)
{
WolframAlpha wolfram = new WolframAlpha(ConfigurationManager.AppSettings["WolframAlphaAppId"]);
string query = "(" + expression1.Replace(" ", "") + ")-(" + expression2.Replace(" ", "") + ")";
QueryResult result = wolfram.Query(query);
result.RecalculateResults();
try
{
double d;
return double.TryParse(result.GetPrimaryPod().SubPods[0].Plaintext, out d) && d == 0.0;
}
catch
{
return false;
}
}
Загрузка и выгрузка сборок с помощью доменов
Создание домена, сборки из файла, создание экземпляра определенного типа и получение объектов с информацией о методах (MethodInfo):
Domain = AppDomain.CreateDomain("MathFuncDomain");
MathFuncObj = _domain.CreateInstanceFromAndUnwrap(FileName, NamespaceName + "." + ClassName);
Type mathFuncObjType = _mathFuncObj.GetType();
Func = mathFuncObjType.GetMethod(FuncName);
FuncDerivative = mathFuncObjType.GetMethod(FuncDerivativeName);
Вычисление результата скомпилированной функции:
return (double)Func.Invoke(_mathFuncObj, new object[] { x })
Выгрузка домена и удаление файла со сборкой:
if (_domain != null)
AppDomain.Unload(Domain);
File.Delete(FileName);
Сравнение сгенерированного IL кода
Финальный IL код является более оптимальным, по сравнению с кодом, сгенерированным стандартным C# компилятором csc.exe в Release режиме, достаточно всего лишь взглянуть на сравнение следующих двух листингов например для функции
x ^ 3 + sin(3 * ln(x * 1)) + x ^ ln(2 * sin(3 * ln(x))) - 2 * x ^ 3| csc.exe .NET 4.5.1 | MathExpressions.NET |
|
|
Любопытно при этом посмотреть, какой при этом получается дизассемблированный C# код в ILSpy для функции, являющейся производной к вышеупомянутой функции, т.е. к
(ln(2 * sin(3 * ln(x))) * x ^ -1 + 3 * ln(x) * cos(3 * ln(x)) * sin(3 * ln(x)) ^ -1 * x ^ -1) * x ^ ln(2 * sin(3 * ln(x))) + 3 * cos(3 * ln(x)) * x ^ -1 + -(3 * x ^ 2)double arg_24_0 = 2.0;
double arg_1A_0 = 3.0;
double num = Math.Log(x);
double num2 = arg_1A_0 * num;
double num3 = Math.Sin(num2);
double num4 = Math.Log(arg_24_0 * num3);
double arg_3B_0 = num4;
double num5 = 1.0 / x;
double arg_54_0 = arg_3B_0 * num5;
double arg_4F_0 = 3.0 * num;
num = Math.Cos(num2);
return (arg_54_0 + arg_4F_0 * num / num3 * num5) * Math.Pow(x, num4) + num * num5 * 3.0 - x * x * 3.0;
Как видим, создалось большое количество локальных переменных для хранения уже рассчитанных результатов функций. Хотя в реальности локальных переменных меньше, потому что, например, для double arg_24_0 = 2.0; не создается локальная переменная, это просто константа.
Конечно, в реальных приложениях подобные выражения редко встречаются, но, тем не менее, описанные оптимизации могут использоваться в других, более прикладных случаях и для лучшего понимания работы компилятора.
Заключение
Во время реализации всего вышеперечисленного на C#, я понял, что функциональный язык больше подходит для таких задач, где требуется произвести что-то связанное с символьными вычислениями и подстановкой. Даже, например, OpenSource система компьютерной алгебры maxima написана на lisp. Кстати, на F# есть реализация символьных вычислений на codeproject, и кода там явно меньше, чем у меня в проекте. Однако реализация данного проекта позволила мне получить больше опыта в разборе выражений, оптимизации, генерации низкоуровневого кода, работе с числами с плавающей точкой и просто в математике.
Для всех заинтересованных я выложил ее на Github: source. Также и доступна сама программа: MathExpressions.NET. При острой необходимости могу ее отрефакторить. Пулл-реквесты приветствуются.
P.S. В сердечке спрятана длинная формула с учетом перестановки слагаемых, множителей и упрощения. Во время ее усложнения использовалась разработанная программа.
UPDATE: Так как никто не отгадал, что зашифровано в сердечке, то выкладываю результат. Данная формула является частным случаем многочлена Матиясевича, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. На википедии также есть информация.