В современном мире часто приходится сталкиваться с проблемой рекомендации товаров или услуг пользователям какой-либо информационной системы. В старые времена для формирования рекомендаций обходились сводкой наиболее популярных продуктов: это можно наблюдать и сейчас, открыв тот же Google Play. Но со временем такие рекомендации стали вытесняться таргетированными (целевыми) предложениями: пользователям рекомендуются не просто популярные продукты, а те продукты, которые наверняка понравятся именно им. Не так давно компания Netflix проводила конкурс с призовым фондом в 1 миллион долларов, задачей которого стояло улучшение алгоритма рекомендации фильмов (подробнее). Как же работают подобные алгоритмы?
В данной статье рассматривается алгоритм коллаборативной фильтрации по схожести пользователей, определяемой с использованием косинусной меры, а также его реализация на python.

Допустим, у нас имеется матрица оценок, выставленных пользователями продуктам, для простоты изложения продуктам присвоены номера 1-9:

Задать её можно при помощи csv-файла, в котором первым столбцом будет имя пользователя, вторым — идентификатор продукта, третьим — выставленная пользователем оценка. Таким образом, нам нужен csv-файл со следующим содержимым:
Для начала разработаем функцию, которая прочитает приведенный выше csv-файл. Для хранения рекомендаций будем использовать стандартную для python структуру данных dict: каждому пользователю ставится в соответствие справочник его оценок вида «продукт»:«оценка». Получится следующий код:
Интуитивно понятно, что для рекомендации пользователю №1 какого-либо продукта, выбирать нужно из продуктов, которые нравятся каким-то пользователям 2-3-4-etc., которые наиболее похожи по своим оценкам на пользователя №1. Как же получить численное выражение этой «похожести» пользователей? Допустим, у нас есть M продуктов. Оценки, выставленные отдельно взятым пользователем, представляют собой вектор в M-мерном пространстве продуктов, а сравнивать вектора мы умеем. Среди возможных мер можно выделить следующие:
Более подробно различные меры и аспекты их применения я собираюсь рассмотреть в отдельной статье. Пока же достаточно сказать, что в рекомендательных системах наиболее часто используются косинусная мера и коэффициент корреляции Танимото. Рассмотрим более подробно косинусную меру, которую мы и собираемся реализовать. Косинусная мера для двух векторов — это косинус угла между ними. Из школьного курса математики мы помним, что косинус угла между двумя векторами — это их скалярное произведение, деленное на длину каждого из двух векторов:
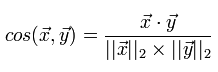
Реализуем вычисление этой меры, не забывая о том, что у нас множество оценок пользователя представлено в виде dict «продукт»:«оценка»
При реализации был использован факт, что скалярное произведение вектора самого на себя дает квадрат длины вектора — это не лучшее решение с точки зрения производительности, но в нашем примере скорость работы не принципиальна.
Итак, у нас есть матрица предпочтений пользователей и мы умеем определять, насколько два пользователя похожи друг на друга. Теперь осталось реализовать алгоритм коллаборативной фильтрации, который состоит в следующем:
В виде формулы этот алгоритм может быть представлен как
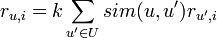
где функция sim — выбранная нами мера схожести двух пользователей, U — множество пользователей, r — выставленная оценка, k — нормировочный коэффициент:
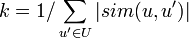
Теперь осталось только написать соответствующий код
Для проверки его работоспособности можно выполнить следующую команду:
Что приведет к следующему результату:
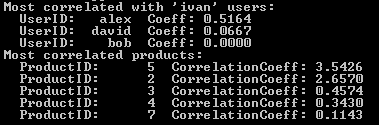
Мы рассмотрели на примере и реализовали один из простейших вариантов коллаборативной фильтрации с использованием косинусной меры сходства. Важно понимать, что существуют другие подходы к коллаборативной фильтрации, другие формулы для вычисления оценок продуктов, другие меры схожести (статья, раздел «See also»). Дальнейшее развитие этой идеи можно вести в следующих направлениях:
В данной статье рассматривается алгоритм коллаборативной фильтрации по схожести пользователей, определяемой с использованием косинусной меры, а также его реализация на python.

Входные данные
Допустим, у нас имеется матрица оценок, выставленных пользователями продуктам, для простоты изложения продуктам присвоены номера 1-9:

Задать её можно при помощи csv-файла, в котором первым столбцом будет имя пользователя, вторым — идентификатор продукта, третьим — выставленная пользователем оценка. Таким образом, нам нужен csv-файл со следующим содержимым:
alex,1,5.0
alex,2,3.0
alex,5,4.0
ivan,1,4.0
ivan,6,1.0
ivan,8,2.0
ivan,9,3.0
bob,2,5.0
bob,3,5.0
david,3,4.0
david,4,3.0
david,6,2.0
david,7,1.0
Для начала разработаем функцию, которая прочитает приведенный выше csv-файл. Для хранения рекомендаций будем использовать стандартную для python структуру данных dict: каждому пользователю ставится в соответствие справочник его оценок вида «продукт»:«оценка». Получится следующий код:
import csv
def ReadFile (filename = "<csv_file_location>"):
f = open (filename)
r = csv.reader (f)
mentions = dict()
for line in r:
user = line[0]
product = line[1]
rate = float(line[2])
if not user in mentions:
mentions[user] = dict()
mentions[user][product] = rate
f.close()
return mentions
Мера схожести
Интуитивно понятно, что для рекомендации пользователю №1 какого-либо продукта, выбирать нужно из продуктов, которые нравятся каким-то пользователям 2-3-4-etc., которые наиболее похожи по своим оценкам на пользователя №1. Как же получить численное выражение этой «похожести» пользователей? Допустим, у нас есть M продуктов. Оценки, выставленные отдельно взятым пользователем, представляют собой вектор в M-мерном пространстве продуктов, а сравнивать вектора мы умеем. Среди возможных мер можно выделить следующие:
- Косинусная мера
- Коэффициент корреляции Пирсона
- Евклидово расстояние
- Коэффициент Танимото
- Манхэттенское расстояние и т.д.
Более подробно различные меры и аспекты их применения я собираюсь рассмотреть в отдельной статье. Пока же достаточно сказать, что в рекомендательных системах наиболее часто используются косинусная мера и коэффициент корреляции Танимото. Рассмотрим более подробно косинусную меру, которую мы и собираемся реализовать. Косинусная мера для двух векторов — это косинус угла между ними. Из школьного курса математики мы помним, что косинус угла между двумя векторами — это их скалярное произведение, деленное на длину каждого из двух векторов:
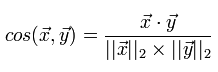
Реализуем вычисление этой меры, не забывая о том, что у нас множество оценок пользователя представлено в виде dict «продукт»:«оценка»
def distCosine (vecA, vecB):
def dotProduct (vecA, vecB):
d = 0.0
for dim in vecA:
if dim in vecB:
d += vecA[dim]*vecB[dim]
return d
return dotProduct (vecA,vecB) / math.sqrt(dotProduct(vecA,vecA)) / math.sqrt(dotProduct(vecB,vecB))
При реализации был использован факт, что скалярное произведение вектора самого на себя дает квадрат длины вектора — это не лучшее решение с точки зрения производительности, но в нашем примере скорость работы не принципиальна.
Алгоритм коллаборативной фильтрации
Итак, у нас есть матрица предпочтений пользователей и мы умеем определять, насколько два пользователя похожи друг на друга. Теперь осталось реализовать алгоритм коллаборативной фильтрации, который состоит в следующем:
- Выбрать L пользователей, вкусы которых больше всего похожи на вкусы рассматриваемого. Для этого для каждого из пользователей нужно вычислить выбранную меру (в нашем случае косинусную) в отношении рассматриваемого пользователя, и выбрать L наибольших. Для Ивана из таблицы, приведенной выше, мы получим следующие значения:

- Для каждого из пользователей умножить его оценки на вычисленную величину меры, таким образом оценки более «похожих» пользователей будут сильнее влиять на итоговую позицию продукта, что можно увидеть в таблице на иллюстрации ниже
- Для каждого из продуктов посчитать сумму калиброванных оценок L наиболее близких пользователей, полученную сумму разделить на сумму мер L выбранных пользователей. Сумма представлена на иллюстрации в строке «sum», итоговое значение в строке «result»
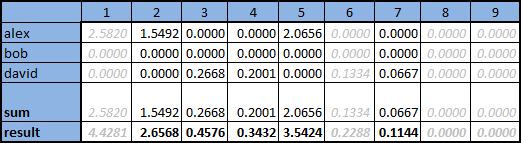
Серым цветом отмечены столбцы продуктов, которые уже были оценены рассматриваемым пользователем и повторно предлагать их ему не имеет смысла
В виде формулы этот алгоритм может быть представлен как
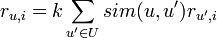
где функция sim — выбранная нами мера схожести двух пользователей, U — множество пользователей, r — выставленная оценка, k — нормировочный коэффициент:
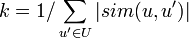
Теперь осталось только написать соответствующий код
import math
def makeRecommendation (userID, userRates, nBestUsers, nBestProducts):
matches = [(u, distCosine(userRates[userID], userRates[u])) for u in userRates if u <> userID]
bestMatches = sorted(matches, key=lambda(x,y):(y,x), reverse=True)[:nBestUsers]
print "Most correlated with '%s' users:" % userID
for line in bestMatches:
print " UserID: %6s Coeff: %6.4f" % (line[0], line[1])
sim = dict()
sim_all = sum([x[1] for x in bestMatches])
bestMatches = dict([x for x in bestMatches if x[1] > 0.0])
for relatedUser in bestMatches:
for product in userRates[relatedUser]:
if not product in userRates[userID]:
if not product in sim:
sim[product] = 0.0
sim[product] += userRates[relatedUser][product] * bestMatches[relatedUser]
for product in sim:
sim[product] /= sim_all
bestProducts = sorted(sim.iteritems(), key=lambda(x,y):(y,x), reverse=True)[:nBestProducts]
print "Most correlated products:"
for prodInfo in bestProducts:
print " ProductID: %6s CorrelationCoeff: %6.4f" % (prodInfo[0], prodInfo[1])
return [(x[0], x[1]) for x in bestProducts]
Для проверки его работоспособности можно выполнить следующую команду:
rec = makeRecommendation ('ivan', ReadFile(), 5, 5)
Что приведет к следующему результату:

Заключение
Мы рассмотрели на примере и реализовали один из простейших вариантов коллаборативной фильтрации с использованием косинусной меры сходства. Важно понимать, что существуют другие подходы к коллаборативной фильтрации, другие формулы для вычисления оценок продуктов, другие меры схожести (статья, раздел «See also»). Дальнейшее развитие этой идеи можно вести в следующих направлениях:
- Оптимизация используемых стуктур данных. При хранении данных в python в виде dict, при каждом обращении к конкретному значению производится вычисление хэша и ситуация становится тем хуже, чем длинее строки названий. В практических задачах для хранения данных можно использовать разреженные матрицы, а вместо текстовых имен пользователей и названий продуктов использовать числовые идентификаторы (пронумеровать всех пользователей и все продукты)
- Оптимизация производительности. Очевидно, что вычислять рекомендацию при каждом обращении пользователя — занятие крайне затратное. Есть несколько вариантов обхода этой проблемы:
- Кластеризация пользователей и вычисление меры схожести только между пользователями, принадлежащими одному кластеру
- Вычисление коэффициентов схожести продукт-продукт. Для этого нужно транспонировать матрицу пользовать-продукт (получится матрица продукт-пользователь), после чего для каждого из продуктов вычислить набор наиболее схожих продуктов, используя ту же косинусную меру и запомнив k ближайших. Это достаточно трудоемкий процесс, поэтому производить его можно один раз в M часов/дней. Но теперь у нас есть список продуктов, похожих на данный, и умножив оценки пользователя на значение меры схожести продуктов, мы получим рекомендацию за O(N*k), где N — количество оценок пользователя
- Подбор меры сходства. Косинусная мера является одной из часто используемых, но выбор меры нужно производить только по результатам анализа данных системы
- Модификация алгоритма фильтрации. Возможно, другой алгоритм фильтрации даст более точные рекомендации в конкретной системе. Опять же, сравнение различных алгоритмов можно производить только в применении к конкретной системе