Фильтр размытия по гауссу (широко известный “gaussian blur” в фотошопе) достаточно часто применяется сам по себе или как часть других алгоритмов обработки изображений. Далее будет описан метод, позволяющий получать размытие со скоростью, не зависящей от радиуса размытия, используя фильтры с бесконечной импульсной характеристикой.
Описание метода есть на английском. Но на русском информации нет. Кроме того, мною были внесены некоторые изменения.
Итак, пусть исходное изображение будет задано яркостью x(m,n). Гаусово размытие с радиусом r считается по формуле
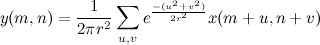
Пределы суммирования по u и v можно выбирать как плюс минус несколько сигм, т.е. радиусов r, что даёт сложность алгоритма порядка O(r2) операций на пиксель. Для больших r и многомегапиксельных изображений не слишком здорово, правда?
Первое ускорение даёт свойство сепарабельности гауссова размытия. То есть, можно провести фильтрацию по оси x для каждой строки, полученное изображение отфильтровать по y по каждому столбцу и получить тот же результат со сложностью O(r) операций на пиксель. Уже лучше. Это свойство мы тоже будем использовать, поэтому дальше все рассуждения будут для одномерного случая, где нужно получить y(n) имея x(n).
В этом нам помогут фильтры с бесконечной импульсной характеристикой. Идея фильтра такова: значения y(n) рекуррентно рассчитываются по формуле:
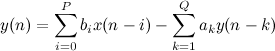
Где ak и bi – некоторые предрасчитанные коэффициенты, а y(n) и x(n) при n<0 полагаются равными нулю.
Часть формулы, зависящая от bi сводится к простой свёртке с конечным ядром. Поскольку мы хотим, чтобы фильтр считал побыстрее, то наш фильтр будем искать для случая P=0, то есть рассматривая один единственный коэффициент b0.
На всякий случай, напомню, что любой линейный фильтр (а БИХ фильтр также является линейным) полностью характеризуется своим откликом на дельта функцию, равную 1 в точке 0, и 0 во всех остальных точках. Часть, зависящая от коэффициентов a при отклике на такую функцию либо разойдётся и уйдёт в бесконечность (этого хотелось бы избежать), либо даст нам красивый убывающий хвост. Например, вот такой:
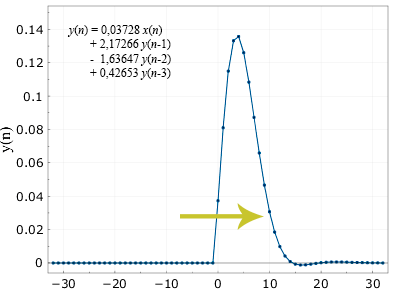
Похоже на гаусс? Ну да, что-то уже есть, но как-то оно кособоко выглядит. Поэтому идея алгоритма будет такой: мы отфильтруем в одну сторону (циклом от 0 до nmax), а потом результат в обратную (от nmax до 0), с теми же коэффициентами. Математически должна получиться строго симметричная кривая (поэтому не важно, фильтровать сначала туда потом обратно, или наоборот). Несколько забегая вперёд, вот что получится если профильтровать это ещё в обратном порядке:
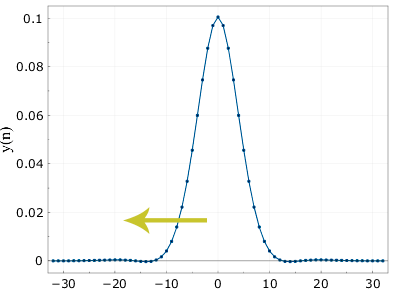
Вот. Почти то, что нам нужно. Почти, потому что на самом деле, конечно, не совсем. Кривая немного заходит в отрицательную область, и вообще отличается от точной гауссовой. Но для большинства приложений всё это вполне приемлемо, кроме того, если нужно считать совсем уж точно, можно повышать порядок фильтра Q.
Итак, осталось рассчитать коэффициенты фильтра a. Далее все формулы пойдут для случая Q=3.
Вообще фильтры изучают с помощью так называемой передаточной функции. Желающие могут прочесть, что это вообще такое, а нам для начала вполне хватит что она просто существует, и имеет определённые свойства. Общий вид этой функции для линейного фильтра будет такой:
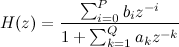
Или для нашего случая Q=3, P=1:
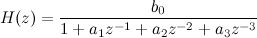
Поскольку в числителе и знаменателе находятся многочлены, их можно разложить на множители. Числитель, в общем случае, даст нам нули (в нашем случае нулей нет), а знаменатель – полюса:
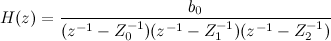
в нашем случае 1/Z0, 1/Z1, 1/Z2. Заметим, что полюса однозначно определяют коэффициенты ak нашего фильтра (все БИХ фильтры, обычно, ищутся именно через полюса, а не напрямую). Кстати, получить коэффициенты по полюсам проще, чем наоборот (для этого нужно перемножить полиномы, а наоборот – решить степенное уравнение).
Самый главный теоретический постулат, который нам пригодиться: если комплексные полюса лежат внутри единичного круга, т.е. по модулю меньше единицы, (или, что тоже самое, обратные значения Z0, Z1, Z2 лежат вне единичного круга), то фильтр будет устойчивым, то результат не убежит в бесконечность.
Отметим также, что назвав произвольные комплексно сопряженные Z0, Z1 и вещественное Z2 (опять же, все по модулю больше единицы) мы можем построить по ним фильтр. В произведении всё превратится в строго вещественные коэффициенты a.
Коэффициент b0 работает как “коэффициент громкости” фильтра.
Итак, задача свелась к определению трёх коэффициентов Z0, Z1, Z2. Поскольку, повторюсь, два из них комплексно сопряженные, а третий вещественные, то нужно найти вещественную и мнимую часть от первого, и вещественную от третьего. То есть, три вещественных числа: real(Z0), im(Z0), Z2
Эти три числа должны выражаться через нужный нам радиус фильтра. Отметим, что в реальности имеет смысл считать для r больше либо равного двум, при меньших значениях быстрее профильтровать умножением.
Дальше я пошёл немного другим путём, чем в работе «Recursive Gaussian Derivative Filters». Там они распространяли случай с r=2 на все другие, а я определил лучшие коэффициенты для всех радиусов от 2 до 2048, с экспоненциальным шагом. Я написал оптимизационный алгоритм, который ищет наиболее близкую кривую по методу минимизации модуля максимальной разницы. Дополнительным условием было сохранение фильтром полной энергии, т.е. чтобы функция x(n)=const переходила саму в себя, что даёт условие
b0=1-(a1+a2+a3)
Я перепробовал разные оптимизационные алгоритмы, и лучшие выдавал немного измененный генетический алгоритм. (Пожалуй, про оптимизацию можно написать отдельную заметку).
Желающие могут посмотреть результаты на google spreadsheet.
Видно, что для случая r=2 результаты отличаются от данных в работе. Почему так, я сказать не могу, при этом по моим расчетам мои коэффициенты дают меньшую, процентов на 40, погрешность.
Дальше я воспользовался не буквой а духом статьи, и стал искать данные как
real(Z0) = cos(W(r)/r)*eA(r)/r
im(Z0) = sin(W(r)/r)*eA(r)/r
Z2 = eB(r)/r
Т.е. дальше нужно просто подобрать три похожие функции, каждая из которых стремится в пределе в константе. Я искал функции в виде отношения
(k3 r3 + k2 r2 + k1 r + k0)/r3
и подобрал коэффициенты самым простым образом — просто использовав Wolfram Mathematica. Кстати, если внимательно изучать графики данных из таблиц, видно что функция имеет несколько пилообразную структуру. Поэтому при аппроксимации мы немного потеряем в точности, но по факту совсем чуть чуть — значения из таблицы дадут ошибку на 10 процентов меньшую, чем полученные полиномами.
Ну вот. Для тех, кто уже запутался что и от чего нужно считать, приведу финальный код функции на С для расчёта коэффициентов:
Всё! Теперь, нужно написать сам код. Расчёт, конечно, нужно производить во float, но современные компьютеры считают на числа с плавающей запятой (особенно с sse) довольно быстро. Программисты из Интел, кстати, озаботились оптимизацией Gauss-IIR фильтров под векторные инструкции процессора уже написали целую статью. Правда, там считают немножко другим методом, но основные способы оптимизации описаны хорошо.
В конце можно дать пример того, что получилось:

Картинка практически не отличается от «честной». Впрочем, если открыть её в фотошопе и поизучать внимательно, разницу найти можно.
P.S. Это правда мой первый пост на Хабре, я мог что-то пропустить. Если будут вопросы, я отвечу в комментариях.
Описание метода есть на английском. Но на русском информации нет. Кроме того, мною были внесены некоторые изменения.
Итак, пусть исходное изображение будет задано яркостью x(m,n). Гаусово размытие с радиусом r считается по формуле
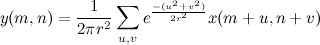
Пределы суммирования по u и v можно выбирать как плюс минус несколько сигм, т.е. радиусов r, что даёт сложность алгоритма порядка O(r2) операций на пиксель. Для больших r и многомегапиксельных изображений не слишком здорово, правда?
Первое ускорение даёт свойство сепарабельности гауссова размытия. То есть, можно провести фильтрацию по оси x для каждой строки, полученное изображение отфильтровать по y по каждому столбцу и получить тот же результат со сложностью O(r) операций на пиксель. Уже лучше. Это свойство мы тоже будем использовать, поэтому дальше все рассуждения будут для одномерного случая, где нужно получить y(n) имея x(n).
В этом нам помогут фильтры с бесконечной импульсной характеристикой. Идея фильтра такова: значения y(n) рекуррентно рассчитываются по формуле:
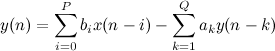
Где ak и bi – некоторые предрасчитанные коэффициенты, а y(n) и x(n) при n<0 полагаются равными нулю.
Часть формулы, зависящая от bi сводится к простой свёртке с конечным ядром. Поскольку мы хотим, чтобы фильтр считал побыстрее, то наш фильтр будем искать для случая P=0, то есть рассматривая один единственный коэффициент b0.
На всякий случай, напомню, что любой линейный фильтр (а БИХ фильтр также является линейным) полностью характеризуется своим откликом на дельта функцию, равную 1 в точке 0, и 0 во всех остальных точках. Часть, зависящая от коэффициентов a при отклике на такую функцию либо разойдётся и уйдёт в бесконечность (этого хотелось бы избежать), либо даст нам красивый убывающий хвост. Например, вот такой:

Похоже на гаусс? Ну да, что-то уже есть, но как-то оно кособоко выглядит. Поэтому идея алгоритма будет такой: мы отфильтруем в одну сторону (циклом от 0 до nmax), а потом результат в обратную (от nmax до 0), с теми же коэффициентами. Математически должна получиться строго симметричная кривая (поэтому не важно, фильтровать сначала туда потом обратно, или наоборот). Несколько забегая вперёд, вот что получится если профильтровать это ещё в обратном порядке:

Вот. Почти то, что нам нужно. Почти, потому что на самом деле, конечно, не совсем. Кривая немного заходит в отрицательную область, и вообще отличается от точной гауссовой. Но для большинства приложений всё это вполне приемлемо, кроме того, если нужно считать совсем уж точно, можно повышать порядок фильтра Q.
Итак, осталось рассчитать коэффициенты фильтра a. Далее все формулы пойдут для случая Q=3.
Вообще фильтры изучают с помощью так называемой передаточной функции. Желающие могут прочесть, что это вообще такое, а нам для начала вполне хватит что она просто существует, и имеет определённые свойства. Общий вид этой функции для линейного фильтра будет такой:
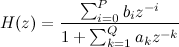
Или для нашего случая Q=3, P=1:
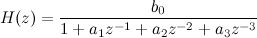
Поскольку в числителе и знаменателе находятся многочлены, их можно разложить на множители. Числитель, в общем случае, даст нам нули (в нашем случае нулей нет), а знаменатель – полюса:
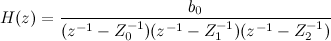
в нашем случае 1/Z0, 1/Z1, 1/Z2. Заметим, что полюса однозначно определяют коэффициенты ak нашего фильтра (все БИХ фильтры, обычно, ищутся именно через полюса, а не напрямую). Кстати, получить коэффициенты по полюсам проще, чем наоборот (для этого нужно перемножить полиномы, а наоборот – решить степенное уравнение).
Самый главный теоретический постулат, который нам пригодиться: если комплексные полюса лежат внутри единичного круга, т.е. по модулю меньше единицы, (или, что тоже самое, обратные значения Z0, Z1, Z2 лежат вне единичного круга), то фильтр будет устойчивым, то результат не убежит в бесконечность.
Отметим также, что назвав произвольные комплексно сопряженные Z0, Z1 и вещественное Z2 (опять же, все по модулю больше единицы) мы можем построить по ним фильтр. В произведении всё превратится в строго вещественные коэффициенты a.
Коэффициент b0 работает как “коэффициент громкости” фильтра.
Итак, задача свелась к определению трёх коэффициентов Z0, Z1, Z2. Поскольку, повторюсь, два из них комплексно сопряженные, а третий вещественные, то нужно найти вещественную и мнимую часть от первого, и вещественную от третьего. То есть, три вещественных числа: real(Z0), im(Z0), Z2
Эти три числа должны выражаться через нужный нам радиус фильтра. Отметим, что в реальности имеет смысл считать для r больше либо равного двум, при меньших значениях быстрее профильтровать умножением.
Дальше я пошёл немного другим путём, чем в работе «Recursive Gaussian Derivative Filters». Там они распространяли случай с r=2 на все другие, а я определил лучшие коэффициенты для всех радиусов от 2 до 2048, с экспоненциальным шагом. Я написал оптимизационный алгоритм, который ищет наиболее близкую кривую по методу минимизации модуля максимальной разницы. Дополнительным условием было сохранение фильтром полной энергии, т.е. чтобы функция x(n)=const переходила саму в себя, что даёт условие
b0=1-(a1+a2+a3)
Я перепробовал разные оптимизационные алгоритмы, и лучшие выдавал немного измененный генетический алгоритм. (Пожалуй, про оптимизацию можно написать отдельную заметку).
Желающие могут посмотреть результаты на google spreadsheet.
Видно, что для случая r=2 результаты отличаются от данных в работе. Почему так, я сказать не могу, при этом по моим расчетам мои коэффициенты дают меньшую, процентов на 40, погрешность.
Дальше я воспользовался не буквой а духом статьи, и стал искать данные как
real(Z0) = cos(W(r)/r)*eA(r)/r
im(Z0) = sin(W(r)/r)*eA(r)/r
Z2 = eB(r)/r
Т.е. дальше нужно просто подобрать три похожие функции, каждая из которых стремится в пределе в константе. Я искал функции в виде отношения
(k3 r3 + k2 r2 + k1 r + k0)/r3
и подобрал коэффициенты самым простым образом — просто использовав Wolfram Mathematica. Кстати, если внимательно изучать графики данных из таблиц, видно что функция имеет несколько пилообразную структуру. Поэтому при аппроксимации мы немного потеряем в точности, но по факту совсем чуть чуть — значения из таблицы дадут ошибку на 10 процентов меньшую, чем полученные полиномами.
Ну вот. Для тех, кто уже запутался что и от чего нужно считать, приведу финальный код функции на С для расчёта коэффициентов:
int gaussCoef(double sigma, double a[3], double *b0)
{
double sigma_inv_4;
sigma_inv_4 = sigma*sigma; sigma_inv_4 = 1.0/(sigma_inv_4*sigma_inv_4);
double coef_A = sigma_inv_4*(sigma*(sigma*(sigma*1.1442707+0.0130625)-0.7500910)+0.2546730);
double coef_W = sigma_inv_4*(sigma*(sigma*(sigma*1.3642870+0.0088755)-0.3255340)+0.3016210);
double coef_B = sigma_inv_4*(sigma*(sigma*(sigma*1.2397166-0.0001644)-0.6363580)-0.0536068);
double z0_abs = exp(coef_A);
double z0_real = z0_abs*cos(coef_W);
double z0_im = z0_abs*sin(coef_W);
double z2 = exp(coef_B);
double z0_abs_2 = z0_abs*z0_abs;
a[2] = 1.0/(z2*z0_abs_2);
a[0] = (z0_abs_2+2*z0_real*z2)*a[2];
a[1] = -(2*z0_real+z2)*a[2];
*b0 = 1.0 - a[0] - a[1] - a[2];
return 0;
};Всё! Теперь, нужно написать сам код. Расчёт, конечно, нужно производить во float, но современные компьютеры считают на числа с плавающей запятой (особенно с sse) довольно быстро. Программисты из Интел, кстати, озаботились оптимизацией Gauss-IIR фильтров под векторные инструкции процессора уже написали целую статью. Правда, там считают немножко другим методом, но основные способы оптимизации описаны хорошо.
В конце можно дать пример того, что получилось:

Картинка практически не отличается от «честной». Впрочем, если открыть её в фотошопе и поизучать внимательно, разницу найти можно.
P.S. Это правда мой первый пост на Хабре, я мог что-то пропустить. Если будут вопросы, я отвечу в комментариях.