Comments 76
Разработка-через-тестирование из будущего: программист просто пишет набор тестов, а компьютер сам генерирует оптимальное синтаксическое дерево будущей программы. :)
Не хочу выглядеть глупо, но why not? Особенно для выделения каких-либо неочевидных зависимостей или же при недостатке данных об этих самых зависимостях.
*slowpoke-mode-on*
Или это был не сарказм?
*slowpoke-mode-off*
*slowpoke-mode-on*
Или это был не сарказм?
*slowpoke-mode-off*
В некоторых случаях этот подход дает интересные результаты уже сегодня: Проверка принадлежности точки многоугольнику.
Я думаю для решения статистических задач этот подход вполне себе подходит.
ТДД нужно, очень, когда мы программируем на императивных языках. Тогда мы создаем две программы: вторая содержит ограничения для первой. Но если бы вторая содержала все ограничения и могла полностью описать все требования, то это декларативный подход. Такие языки уже есть. Без никаких генетических алгоритмов сразу строят абстрактное синтаксическое дерево.
Плюсы декларативных языков: меньше возможностей ошибиться.
Минусы: еще нет таких очень хороших языков, близких к естественному. И как правило, требуют лучшей подготовки.
Т.к. в декларативных языках все таки можно ошибаться, описывая «что» хотите от программы, то и там бывает полезно ТДД. Т.е. тесты — это то же самое, но сделанное по другому. Вероятность ошибиться перемножается. Т.е. заметно падает.
Если же взять ваше утверждение, что не нужно будет писать основную программу, а только тесты, то это (исходя из того, что я написал), бессмысленно. Потому что это уже не тесты, а просто какой-то язык выражения требований.
Плюсы декларативных языков: меньше возможностей ошибиться.
Минусы: еще нет таких очень хороших языков, близких к естественному. И как правило, требуют лучшей подготовки.
Т.к. в декларативных языках все таки можно ошибаться, описывая «что» хотите от программы, то и там бывает полезно ТДД. Т.е. тесты — это то же самое, но сделанное по другому. Вероятность ошибиться перемножается. Т.е. заметно падает.
Если же взять ваше утверждение, что не нужно будет писать основную программу, а только тесты, то это (исходя из того, что я написал), бессмысленно. Потому что это уже не тесты, а просто какой-то язык выражения требований.
Минусы: еще нет таких очень хороших языков, близких к естественному
SQL
Написано же — хороших.
Да, не плохой. Но всё же способ выражения на нем мыслей несколько далек от естественного языка. И хотя на нем можно выражать довольно сложные мысли — не так сложно и ошибиться в достаточно большом запросе.
Запрос, написанный на страницу не так и легко читается.
Есть надежда, что в будущем появятся языки, более близкие к естественным языкам и позволяющие описывать прямо use-cases
Запрос, написанный на страницу не так и легко читается.
Есть надежда, что в будущем появятся языки, более близкие к естественным языкам и позволяющие описывать прямо use-cases
Интересно. А можно что-нибудь сказать о сходимости метода для какой либо области хотя бы? Я имею в виду аналитически. Или пока что это только практический результат, правильно?
А на сложных формулах что-нибудь похожее на правду получается?
Я восновном проверял на не очень сложных формулах, например:

Результат:


Результат:

Ещё пробовал искать производные, например, для функции f(x) = x^3 + 10*x + 3^x
Была найдена такая производная:
((((3.0227743447403608 ^ x) + ((-12.239440411314542) + (2.102455478564486 ^ x))) + (0.13948571196849002 ^ ((-2.2335077015658515) + (0.5050189120240571 ^ x)))) + ((((0.7108684661206528 + x) + x) + (-11.765417190571963)) * x))
Если результат упростить, то получится даже немного похоже на правду
На самом деле, когда я упомянул про оптимизацию коэффициентов каждого дерева — пришлось ограничить количество итераций генетического алгоритма до 50 (для того чтоб всё работало быстро), поэтому, иногда коэффициенты синтаксического дерева не успевают оптимизироваться в полной мере, что, в общем, сказывается на результатах не в лучшую сторону.
Была найдена такая производная:
((((3.0227743447403608 ^ x) + ((-12.239440411314542) + (2.102455478564486 ^ x))) + (0.13948571196849002 ^ ((-2.2335077015658515) + (0.5050189120240571 ^ x)))) + ((((0.7108684661206528 + x) + x) + (-11.765417190571963)) * x))
Если результат упростить, то получится даже немного похоже на правду
На самом деле, когда я упомянул про оптимизацию коэффициентов каждого дерева — пришлось ограничить количество итераций генетического алгоритма до 50 (для того чтоб всё работало быстро), поэтому, иногда коэффициенты синтаксического дерева не успевают оптимизироваться в полной мере, что, в общем, сказывается на результатах не в лучшую сторону.
Интересное начинается, когда экстремумов несколько и не понятно под какой оптимизироваться.
А производная искалась точно так же, только для разностей?
А производная искалась точно так же, только для разностей?
Для поиска производной я немного изменил фитнесс функцию:
И опять же, для ускорения работы — я рассматривал только небольшой интервал значений x: от -10 до +11
public double fitness(Expression expression, Context context) {
double delt = 0;
for (int x = -10; x < 11; x += 0.5) {
// искомое значение производной
double target = (this.f(x + dx) - this.f(x)) / dx;
context.setVariable("x", x);
double evolved = expression.eval(context);
delt += this.sqr(target - evolved);
}
return delt;
}
// функция, чью производную мы ищем
private double f(double x) {
return x * x * x + 10 * x + Math.pow(3, x);
}
И опять же, для ускорения работы — я рассматривал только небольшой интервал значений x: от -10 до +11
Да, с несколькими экстремумами ситуация выглядит немного сложнее.
Но хочу обратить внимание на то, что мы оперируем функциями и комбинациями функций. Таким образом, мы можем получить синтаксическое дерево, которое соответствует функции с несколькими экстремумами (а затем оптимизировать коэффициенты в соответствии с тренировочными данными)
Но хочу обратить внимание на то, что мы оперируем функциями и комбинациями функций. Таким образом, мы можем получить синтаксическое дерево, которое соответствует функции с несколькими экстремумами (а затем оптимизировать коэффициенты в соответствии с тренировочными данными)
Простой тест: убрать из числа доступных любую одну трансцендентную функцию (например, sin) и запустить построение аппроксимирующей формулы при разных ограничениях на глубину дерева. И потом нарисовать аналогичный график, только в зависомости не от шага оптимизации, а от глубины дерева. Идея такая: либо (почти невероятно) алгоритм сможет поймать правильную тригонометрическую формулу (т.е. выразит sin через cos), либо начнет строить последовательность все более точных аппроксимаций. Во втором случае интересно посмотреть на структуру получаемых приближенных формул.
Спасибо Вам за идею. Решил проверить — получить формулу для синуса, не имея функции sin.
Для этого создал следующую обучающую выборку (где f(x) — значения синуса x):
Провёл эксперимент несколько раз. Ниже приведены полученные результаты:
Для этого создал следующую обучающую выборку (где f(x) — значения синуса x):
sin_as_cos.txt
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS
# set which functions to use:
ADD SUB MUL DIV SQRT POW COS
# looking for:
f(x) - ?
# define training set:
f(-5) = 0.958924275
f(-4.6) = 0.993691004
f(-4.2) = 0.871575772
f(-3.8) = 0.611857891
f(-3.4) = 0.255541102
f(-3) = -0.141120008
f(-2.6) = -0.515501372
f(-2.2) = -0.808496404
f(-1.8) = -0.973847631
f(-1.4) = -0.98544973
f(-1) = -0.841470985
f(-0.6) = -0.564642473
f(-0.2) = -0.198669331
f(0.2) = 0.198669331
f(0.6) = 0.564642473
f(1) = 0.841470985
f(1.4) = 0.98544973
f(1.8) = 0.973847631
f(2.2) = 0.808496404
f(2.6) = 0.515501372
f(3) = 0.141120008
f(3.4) = -0.255541102
f(3.8) = -0.611857891
f(4.2) = -0.871575772
f(4.6) = -0.993691004
threshold = 0.5
Провёл эксперимент несколько раз. Ниже приведены полученные результаты:
- f(x) = cos((((x — 0.20866701892617723) + 0.20909776128069524) + (-1.5658757184422276)))
После упрощения:
f(x) = cos(x — 1.56544498)
а это почти cos(x — pi/2)
лог экспериментаStart time is: Thu Dec 20 02:09:16 EET 2012 f(x) = 0.037473612748792906 1 13.1066035437915 2 13.1066035437915 f(x) = 0.03907633650413578 3 13.106596972914716 f(x) = ((x * (-0.0872113058946149)) + 0.014906325070420667) 4 12.655025376552377 f(x) = (0.13723422167838573 / x) 5 12.157457270158343 6 12.157457270158343 f(x) = (0.13723422167838573 / (x * 1.0913808377181144)) 7 12.152326784266156 8 12.152326784266156 f(x) = (3.2071455614529727 / (x * 25.114850968636148)) 9 12.152068404736541 f(x) = (3.595526544914747 / ((x * 25.77776235214153) * 1.0913808377181144)) 10 12.152067661286328 f(x) = (0.7306468226024925 / (x + ((3.1952852003281116 / (x * 25.70161792899045)) * 2.623353842188707))) 11 9.952938064507393 f(x) = (0.7306468226024925 / (x + (((3.1952852003281116 / (14.680761568160436 * x)) * 1.39406585192928) * 1.075844125197815))) 12 9.952936408450574 13 9.952936408450574 14 9.952936408450574 f(x) = cos(((-7.899669176555985) / ((x + (-2.934551771761199)) + 1.2773079814532693))) 15 5.945158111235378 16 5.945158111235378 f(x) = cos(((-7.173167456475843) / (((x - 0.20866701892617723) + 0.20909776128069524) + (-1.6400760520463233)))) 17 4.078430742322765 f(x) = cos(((-7.45261054740821) / (((x - 4.329856978342905) + 4.371028455719269) + (-1.6400760520463233)))) 18 2.733571097513842 f(x) = cos((((x - 0.20866701892617723) + 0.20909776128069524) + (-1.5658757184422276))) 19 3.3949567063295085E-4 Best function is: f(x) = cos((((x - 0.20866701892617723) + 0.20909776128069524) + (-1.5658757184422276))) End time is: Thu Dec 20 02:09:25 EET 2012
- f(x) = cos(((-1.07016828426169) * ((x / x) * (x + 4.4401611735732125))))
После упрощения:
f(x) = cos(-1.07016828426169 * x — 4.75171966) = cos(1.07016828426169 * x + 4.75171966)
а это почти cos(x + 3*pi/2)
лог экспериментаStart time is: Thu Dec 20 02:11:58 EET 2012 f(x) = 0.030868250151864896 1 13.107986059245036 f(x) = 0.03767074767874057 2 13.106595808307668 f(x) = 0.038242426449158984 3 13.106584363757857 4 13.106584363757857 5 13.106584363757857 6 13.106584363757857 f(x) = (0.1637990150606723 / x) 7 12.230665733051994 f(x) = (0.13705836621394107 / x) 8 12.15725800536878 9 12.15725800536878 f(x) = ((0.1481202255848797 / x) * 0.8684798749213931) 10 12.152109398402798 11 12.152109398402798 f(x) = (0.12857591793327128 / x) 12 12.152103249788755 f(x) = ((0.020376091331116397 / x) * 6.271785421060187) 13 12.152067673004629 14 12.152067673004629 15 12.152067673004629 16 12.152067673004629 17 12.152067673004629 f(x) = ((0.46601388716913195 ^ x) * 0.02977298399532957) 18 11.469845817953859 f(x) = (((-0.38967085673639446) / ((4.404835173431312 ^ x) / ((-0.08138602455387023) / x))) * (-0.09385199865456717)) 19 10.911993456710471 f(x) = (((-0.1439165901739734) / ((4.457965327030093 ^ x) / ((-0.23419484479312658) / x))) * (-0.09385199865456717)) 20 10.844524333414348 21 10.844524333414348 f(x) = ((0.5666114085540572 / ((0.5348028282775066 ^ x) / (cos((-1.5394326500896378)) / x))) * ((x * (-4.3285907551309215)) - (-9.400020532885092))) 22 10.587827937080267 f(x) = ((0.1488277396985822 / ((-6.499878077275849) / ((1.667112028884965 ^ x) / ((-3.4574956828857646) / x)))) * ((x * (-4.742415091725814)) - (-17.426395027916122))) 23 9.845309875059357 24 9.845309875059357 25 9.845309875059357 f(x) = ((0.019835272236428114 / ((1.4762453312970956 ^ x) / ((x / x) * (x + 3.322468527485495)))) * ((x / x) * (x + (-1.0677662167272803)))) 26 9.611591802099714 f(x) = (((-0.11842972705153176) / ((x * x) / ((3.1353175097938144 ^ x) / ((-12.711280290000289) / x)))) * ((x * (-3.747429583149386)) - (-13.682941331058357))) 27 9.441749174052777 f(x) = (((((-3.9985992143686104) / ((-11.860791526742453) / (x / (-12.255149129698886)))) * (-5.083919364763941)) / ((0.9374635931326201 ^ x) / (((x / (-4.24828079172007)) / x) * (x + (-3.7192102312585376))))) * ((x / x) * (x + 3.5489201296979966))) 28 3.2474458505656605 29 3.2474458505656605 f(x) = cos(((((0.7891062240951006 / (37.690057096649355 / x)) * (-3.9700337867889055)) / ((2.1459450244373666 ^ x) / ((x / x) * ((-31.82073084338193) + x)))) * ((x / x) * (x + 3.8341848367144498)))) 30 2.751772332932753 31 2.751772332932753 32 2.751772332932753 f(x) = cos(((-1.104233492883234) * ((x / x) * (x + 4.176966445681568)))) 33 0.9796598588054801 f(x) = cos((1.0878741299861896 * ((x / x) * (x + 4.407430173983707)))) 34 0.6471346736176921 f(x) = cos(((-1.07016828426169) * ((x / x) * (x + 4.4401611735732125)))) 35 0.39445546562024103 Best function is: f(x) = cos(((-1.07016828426169) * ((x / x) * (x + 4.4401611735732125)))) End time is: Thu Dec 20 02:12:29 EET 2012
- f(x) = cos(((-1.5518824117603933) — ((x * (-22.779793630567173)) * ((0.9905590241810334 ^ x) / 22.778425607844536))))
Опять получили немного запутанную формулу. Хотя, легко заметить, что (0.9905590241810334 ^ x) это почти (1 ^ x) — а значит никак на результирующую формулу влияет. Затем, можно сократить числитель и знаменатель — 22.779793630567173
Таким образом, приходим к формуле:
f(x) = cos(-1.5518824117603933 + x)
а это почти cos(x — pi/2)
лог экспериментаStart time is: Thu Dec 20 02:14:58 EET 2012 f(x) = (x * (-0.03497647400759352)) 1 12.569697409104204 f(x) = (0.03206375777473447 - (x / 17.859742523423733)) 2 12.45310280520347 f(x) = (0.03206375777473447 / (x / 3.983422951936845)) 3 12.152068113028749 4 12.152068113028749 f(x) = (0.16410654890797227 - ((2.0299865145513394 ^ x) / 27.160308551872905)) 5 11.458518951142699 6 11.458518951142699 f(x) = ((-0.08190782796508467) - ((x * 0.3250906200640813) * ((0.5612667000580951 ^ x) / 25.142726236353084))) 7 10.658531610257057 f(x) = ((-0.1820149022978066) - ((x * 0.09015777715283968) * ((0.4280416776009639 ^ x) / 21.065084851380853))) 8 10.516453362951314 f(x) = ((-0.01503108962299926) - ((x * (-24.265371409776968)) * (((0.7310665285787377 ^ x) ^ x) / 19.010083617783746))) 9 5.926306763301507 f(x) = (0.033809751868219884 - ((x * (-22.683745105291987)) * (((0.7310665285787377 ^ x) ^ x) / 17.834566430135432))) 10 5.855312350773518 f(x) = (0.033809751868219884 - ((x * (-22.683745105291987)) * (((0.7310665285787377 ^ x) ^ x) / 17.79616422156097))) 11 5.855294223104098 12 5.855294223104098 f(x) = (0.033809751868219884 - ((x * (-23.19192196847812)) * (((0.717967820948241 ^ x) ^ x) / 17.386188149870783))) 13 5.836810741669103 f(x) = (0.033809751868219884 - ((x * (-21.669518751123967)) * (((0.717967820948241 ^ x) ^ x) / 16.287254620910687))) 14 5.836761497328263 15 5.836761497328263 f(x) = (0.038546517497714206 - ((x * (-21.669518751123967)) * (((0.717967820948241 ^ x) ^ x) / 16.287254620910687))) 16 5.836229539440452 17 5.836229539440452 f(x) = (0.03843417466089871 - ((x * (-21.669518751123967)) * (((0.717967820948241 ^ x) ^ x) / 16.287254620910687))) 18 5.836229167974826 19 5.836229167974826 20 5.836229167974826 21 5.836229167974826 22 5.836229167974826 23 5.836229167974826 24 5.836229167974826 25 5.836229167974826 26 5.836229167974826 27 5.836229167974826 28 5.836229167974826 29 5.836229167974826 30 5.836229167974826 31 5.836229167974826 32 5.836229167974826 33 5.836229167974826 34 5.836229167974826 35 5.836229167974826 36 5.836229167974826 f(x) = (0.03843417466089871 - ((x * (-21.669518751123967)) * (((0.7175444245047398 ^ x) ^ x) / 16.26151878069896))) 37 5.836200483976189 38 5.836200483976189 39 5.836200483976189 f(x) = (0.03843417466089871 - ((x * (-21.669518751123967)) * (((0.7175444245047398 ^ x) ^ x) / 16.262705747349774))) 40 5.836200268757786 41 5.836200268757786 42 5.836200268757786 43 5.836200268757786 f(x) = (0.03843417466089871 - ((x * (-21.662524193965517)) * (((0.7175444245047398 ^ x) ^ x) / 16.262705747349774))) 44 5.83620024612793 45 5.83620024612793 46 5.83620024612793 47 5.83620024612793 f(x) = (0.03843417466089871 - ((x * (-21.667776661667226)) * (((0.7175444245047398 ^ x) ^ x) / 16.262705747349774))) 48 5.836200121399585 49 5.836200121399585 f(x) = (0.03843417466089871 - ((x * (-21.662524193965517)) * (((0.7175444245047398 ^ x) ^ x) / 16.26141837828798))) 50 5.8362001114409825 51 5.8362001114409825 52 5.8362001114409825 53 5.8362001114409825 54 5.8362001114409825 55 5.8362001114409825 56 5.8362001114409825 57 5.8362001114409825 58 5.8362001114409825 59 5.8362001114409825 f(x) = (0.03843417466089871 - ((x * (-24.624664221314188)) * (((0.7175444245047398 ^ x) ^ x) / 18.482635204699278))) 60 5.836200086756856 61 5.836200086756856 62 5.836200086756856 63 5.836200086756856 64 5.836200086756856 65 5.836200086756856 66 5.836200086756856 67 5.836200086756856 68 5.836200086756856 69 5.836200086756856 70 5.836200086756856 71 5.836200086756856 72 5.836200086756856 f(x) = (0.03843417466089871 - ((x * (-23.803425055908484)) * (((0.7175444245047398 ^ x) ^ x) / 17.866721331430185))) 73 5.836200071940088 74 5.836200071940088 75 5.836200071940088 76 5.836200071940088 77 5.836200071940088 f(x) = (((x * (-21.727813149886583)) * (((0.444473883735897 ^ x) ^ x) / 25.877440479220724)) - ((x * (-27.869805964415654)) * (((0.7175444245047398 ^ x) ^ x) / 16.054058406243342))) 78 5.753786607216474 f(x) = cos(((-1.5518824117603933) - ((x * (-22.779793630567173)) * ((0.9905590241810334 ^ x) / 22.778425607844536)))) 79 0.06523396656992454 Best function is: f(x) = cos(((-1.5518824117603933) - ((x * (-22.779793630567173)) * ((0.9905590241810334 ^ x) / 22.778425607844536)))) End time is: Thu Dec 20 02:17:52 EET 2012
- Хотя, один раз всё таки получился полином:
f(x) = ((-22.66355680142012) / ((15.948637956747325 / (((-2.6050273232187884) / x) — (x * (-0.2602149380973864)))) — (17.992754706738232 / x)))

лог экспериментаStart time is: Thu Dec 20 03:06:30 EET 2012 f(x) = (0.18206317394353455 / x) 1 12.3306847201965 2 12.3306847201965 f(x) = (0.13096000716683331 / x) 3 12.152669766801575 4 12.152669766801575 f(x) = (0.12762196997306274 / x) 5 12.152069805558092 6 12.152069805558092 7 12.152069805558092 f(x) = (0.3346849273504282 / ((((-22.4152051827909) * x) + 40.960688022849595) / x)) 8 12.148014860354863 f(x) = ((-0.03796031129649258) / (cos(x) / ((-2.9198621819690938) / x))) 9 11.638011754782829 10 11.638011754782829 f(x) = ((-20.631874183396533) / (((-9.207249236246206) / x) - (x * 27.91345503131871))) 11 9.952693006480558 12 9.952693006480558 13 9.952693006480558 f(x) = ((-11.825393899136301) / ((27.294600788294975 / ((0.5155794242305176 / x) - (x * 17.31342263836807))) - (x * 20.565965766798282))) 14 9.888627753702877 f(x) = ((-15.532470172735072) / ((25.778228513107628 / ((0.18734779505625987 / x) - (x * 6.391452889555231))) - (x * 21.629379422632773))) 15 9.792881118418999 f(x) = ((-11.825393899136301) / ((41.90109261338367 / ((0.46759657320866577 / x) - (x * 15.120516570080058))) - (x * 17.102239047167586))) 16 9.791571430938934 f(x) = ((-22.66355680142012) / ((15.948637956747325 / (((-2.6050273232187884) / x) - (x * (-0.2602149380973864)))) - (17.992754706738232 / x))) 17 0.3622781954825648 Best function is: f(x) = ((-22.66355680142012) / ((15.948637956747325 / (((-2.6050273232187884) / x) - (x * (-0.2602149380973864)))) - (17.992754706738232 / x))) End time is: Thu Dec 20 03:06:40 EET 2012
(небольшое уточнение к графику: в точке x = 0 — асимптота, но так как точка 0 не входила в обучающую выборку, то при построении графика, я её случайно «проскочил»)
Интересно, но с тестом я поторопился. Правильнее будет вовсе убрать тригонометрические формулы (sin и cos убрать, tan можно оставить) и все же посмотреть, как погрешность зависит от разрешенной глубины дерева. Одновременно интересно посмотреть, что будет происходить, если таблицу значений задавать на все более длинном отрезке.
Провёл эксперимент по аппроксимации синуса, без использования тригонометрических функций (используя только операции складывания, вычитания, умножения, деления, возведения в степень и взятия корня)
В результате — получил полином, который аппроксимирует функцию синуса на заданном промежутке:
f(x) = ((x * (((-28.637448958589324) + (x * x)) / ((21.239955408627964 / (x + (-3.2072451559334034))) / (3.3336507016309875 + x)))) / 16.2284520613964)

Эксперименты, с различными ограничениями на максимальную глубину дерева ещё в процессе
Исходный файл с тренировочными данными
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS
# set which functions to use:
ADD SUB MUL DIV SQRT POW
# looking for:
f(x) - ?
# define training set:
f(-5) = 0.958924275
f(-4.6) = 0.993691004
f(-4.2) = 0.871575772
f(-3.8) = 0.611857891
f(-3.4) = 0.255541102
f(-3) = -0.141120008
f(-2.6) = -0.515501372
f(-2.2) = -0.808496404
f(-1.8) = -0.973847631
f(-1.4) = -0.98544973
f(-1) = -0.841470985
f(-0.6) = -0.564642473
f(-0.2) = -0.198669331
f(0) = 0
f(0.2) = 0.198669331
f(0.6) = 0.564642473
f(1) = 0.841470985
f(1.4) = 0.98544973
f(1.8) = 0.973847631
f(2.2) = 0.808496404
f(2.6) = 0.515501372
f(3) = 0.141120008
f(3.4) = -0.255541102
f(3.8) = -0.611857891
f(4.2) = -0.871575772
f(4.6) = -0.993691004
threshold = 0.5
В результате — получил полином, который аппроксимирует функцию синуса на заданном промежутке:
f(x) = ((x * (((-28.637448958589324) + (x * x)) / ((21.239955408627964 / (x + (-3.2072451559334034))) / (3.3336507016309875 + x)))) / 16.2284520613964)

Лог эксперимента
Start time is: Mon Dec 24 21:20:27 EET 2012
f(x) = ((x * 3.1630717262131376) / (-55.751683077133))
1 12.470828286593806
2 12.470828286593806
f(x) = ((x * 3.1630717262131376) / (-55.76553839255925))
3 12.47082827728798
4 12.47082827728798
f(x) = ((x * 0.9949679900764461) / (-17.541037248840254))
5 12.470828274502146
6 12.470828274502146
f(x) = ((x * ((x / 0.24485475450143368) / (9.854722419372969 / (0.1785463411440209 + x)))) / (-51.49422863193457))
7 9.308217623905621
f(x) = ((x * ((x / 0.40104184749153204) / (6.4182649499699105 / (0.052399290993697 + x)))) / (-47.34388178550898))
8 9.302841405933153
9 9.302841405933153
f(x) = ((x * ((x / 0.24485475450143368) / (9.854722419372969 / (0.05192548614521364 + x)))) / (-50.350061089343605))
10 9.302817992891397
f(x) = ((x * ((x / 0.24485475450143368) / (9.854722419372969 / (0.07142331100659893 + x)))) / (-50.350061089343605))
11 9.302771398232064
12 9.302771398232064
13 9.302771398232064
f(x) = ((x * ((x / 2.0533282898391576) / (1.8715544471864307 / (0.07135632922700297 + x)))) / (-31.597742741151393))
14 9.302769883027961
15 9.302769883027961
16 9.302769883027961
17 9.302769883027961
18 9.302769883027961
19 9.302769883027961
20 9.302769883027961
21 9.302769883027961
22 9.302769883027961
23 9.302769883027961
f(x) = ((x * ((x / 2.0533282898391576) / (1.8715544471864307 / (0.06551706960346748 + x)))) / (-31.604995146547317))
24 9.30276797484784
25 9.30276797484784
26 9.30276797484784
27 9.30276797484784
28 9.30276797484784
29 9.30276797484784
f(x) = ((x * (((x / 8.857722754797118) / (2.6551707309632526 / (x + 35.42462283671099))) / (5.464423135144728 / ((-0.39500736529583036) + x)))) / (-32.659737034898576))
30 9.302210185277525
f(x) = ((x * ((6.680648069500437 / (2.6551707309632526 / (x + 3.6592487400627496))) / (2.6443709583155646 / ((-3.5578768847585587) + x)))) / (-30.830217950916406))
31 3.4255888723788033
32 3.4255888723788033
33 3.4255888723788033
34 3.4255888723788033
35 3.4255888723788033
36 3.4255888723788033
37 3.4255888723788033
f(x) = ((((-3.4499225016535195) + x) * (x / (1.2515222248502815 / (3.7938656508895163 + x)))) / (-25.109433521560973))
38 3.405619015538551
f(x) = ((x * (((-3.482346082966841) + x) / (1.1253837525672576 / (3.714227703825927 + x)))) / (-28.336457289208397))
39 3.377886419645044
f(x) = ((x * ((3.735514032671002 + x) / (1.520701195188931 / ((-3.5390881257410745) + x)))) / (-20.512481273437082))
40 3.3675017425027374
41 3.3675017425027374
f(x) = ((x * (((-3.5325640324244243) + x) / (1.1178824947277812 / (3.7667842805750538 + x)))) / (-27.918607440362756))
42 3.366320705519485
43 3.366320705519485
f(x) = ((x * ((21.57790360307947 + x) / ((15.591683015361514 / ((-3.5424250936223514) + x)) / (3.6225272226680865 + x)))) / (-41.57688526816358))
44 3.1012409075624583
45 3.1012409075624583
f(x) = ((x * ((3.572817532610448 + x) / ((22.584809854422687 / (18.974396425768152 + x)) / ((-3.5747295662481573) + x)))) / (-25.32540014476279))
46 3.0771318820680706
47 3.0771318820680706
48 3.0771318820680706
49 3.0771318820680706
50 3.0771318820680706
51 3.0771318820680706
f(x) = ((x * ((3.572817532610448 + x) / ((24.667037538178697 / (x + 18.170833314646938)) / ((-3.6144452483304836) + x)))) / (-21.871869029168302))
52 3.0584324507379494
53 3.0584324507379494
54 3.0584324507379494
55 3.0584324507379494
56 3.0584324507379494
57 3.0584324507379494
58 3.0584324507379494
59 3.0584324507379494
60 3.0584324507379494
61 3.0584324507379494
62 3.0584324507379494
63 3.0584324507379494
64 3.0584324507379494
65 3.0584324507379494
66 3.0584324507379494
67 3.0584324507379494
68 3.0584324507379494
69 3.0584324507379494
70 3.0584324507379494
71 3.0584324507379494
f(x) = ((x * (((-11.347781713226535) + (x * x)) / ((26.70985281041323 / (5.9405385441572705 + x)) / ((-6.365654381745506) + x)))) / 22.788185829488683)
72 0.7608948240547206
73 0.7608948240547206
74 0.7608948240547206
75 0.7608948240547206
76 0.7608948240547206
f(x) = ((x * (((-11.008088011418987) + (x * x)) / ((25.422465316844516 / (x + 5.833553150936389)) / ((-5.788920923994368) + x)))) / 19.641063491031723)
77 0.5114211104584352
78 0.5114211104584352
79 0.5114211104584352
80 0.5114211104584352
81 0.5114211104584352
82 0.5114211104584352
83 0.5114211104584352
84 0.5114211104584352
85 0.5114211104584352
f(x) = ((x * (((-28.637448958589324) + (x * x)) / ((21.239955408627964 / (x + (-3.2072451559334034))) / (3.3336507016309875 + x)))) / 16.2284520613964)
86 0.2643748704212682
Best function is:
f(x) = ((x * (((-28.637448958589324) + (x * x)) / ((21.239955408627964 / (x + (-3.2072451559334034))) / (3.3336507016309875 + x)))) / 16.2284520613964)
End time is: Mon Dec 24 21:22:13 EET 2012
Эксперименты, с различными ограничениями на максимальную глубину дерева ещё в процессе
Спасибо, очень интересно. Еще интереснее было бы загнать алгоритм поближе к пределу его возможностей, увеличивая длину интервала аппроксимации при фиксированной глубине дерева.
Попытался сам запустить Ваш бинарник (для начала на приведенном Вами последнем исходном файле), но не получилось:
ltwood@ltwood-home:~/tmp/sregr$ java -jar symbolic_regression_1.0.jar data.txt
Exception in thread «main» java.lang.NumberFormatException: For input string: «threshold»
at sun.misc.FloatingDecimal.readJavaFormatString(FloatingDecimal.java:1242)
at java.lang.Double.parseDouble(Double.java:527)
at com.lagodiuk.gp.symbolic.example.Main.getTrainingData(Main.java:155)
at com.lagodiuk.gp.symbolic.example.Main.main(Main.java:39)
ltwood@ltwood-home:~/tmp/sregr$ java -version
java version «1.6.0_24»
OpenJDK Runtime Environment (IcedTea6 1.11.5) (6b24-1.11.5-0ubuntu1~12.04.1)
OpenJDK Server VM (build 20.0-b12, mixed mode)
Попытался сам запустить Ваш бинарник (для начала на приведенном Вами последнем исходном файле), но не получилось:
ltwood@ltwood-home:~/tmp/sregr$ java -jar symbolic_regression_1.0.jar data.txt
Exception in thread «main» java.lang.NumberFormatException: For input string: «threshold»
at sun.misc.FloatingDecimal.readJavaFormatString(FloatingDecimal.java:1242)
at java.lang.Double.parseDouble(Double.java:527)
at com.lagodiuk.gp.symbolic.example.Main.getTrainingData(Main.java:155)
at com.lagodiuk.gp.symbolic.example.Main.main(Main.java:39)
ltwood@ltwood-home:~/tmp/sregr$ java -version
java version «1.6.0_24»
OpenJDK Runtime Environment (IcedTea6 1.11.5) (6b24-1.11.5-0ubuntu1~12.04.1)
OpenJDK Server VM (build 20.0-b12, mixed mode)
каковы экстраполяционные свойства у данного метода по вашему опыту?
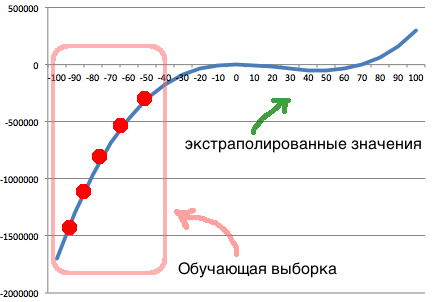
Удаётся реконструировать формулу, даже в случае небольшого количества точек, равномерно распределённых по монотонному участку искомой функции.
Например:
Пусть искомая функция будет f(x) = x^3 — 70*(x^2)
Входные данные — будут точки с монотонного интервала [-100… -40]
Например:
Пусть искомая функция будет f(x) = x^3 — 70*(x^2)
Входные данные — будут точки с монотонного интервала [-100… -40]
файл с входными данными
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS
# set which functions to use:
ADD MUL SUB POW DIV
# looking for:
f(x) - ?
# define training set:
f(-100) = -1700000
f(-90) = -1296000
f(-80) = -960000
f(-70) = -686000
f(-60) = -468000
f(-50) = -300000
f(-40) = -176000
(продолжение предыдущего комментария habrahabr.ru/post/163195/#comment_5611549)
В результате получаем формулу:
f(x) = ((x * (((-13.242522576569776) + (x — (-49.47522269762757))) * x)) — ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
После преобразований:
f(x) = x^3 — 69 * x^2
В результате получаем формулу:
f(x) = ((x * (((-13.242522576569776) + (x — (-49.47522269762757))) * x)) — ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
После преобразований:
f(x) = x^3 — 69 * x^2

лог эксперимента
Start time is: Thu Dec 20 05:42:45 EET 2012
f(x) = (86.57304694845936 * x)
1 6.222169286489249E12
f(x) = (144.6778659232081 * x)
2 6.16902774680368E12
f(x) = (134.17750912815694 * (92.71961934899491 * x))
3 5.590600898187449E11
4 5.590600898187449E11
5 5.590600898187449E11
6 5.590600898187449E11
7 5.590600898187449E11
f(x) = (49.69169866316818 * (x * (x * (-3.1677184236399905))))
8 5.0055596992864105E10
9 5.0055596992864105E10
f(x) = (56.48068300981558 * (((-20.863130437536775) + (x - (-43.12637699374933))) * (x * (-3.7782588026154613))))
10 3.9592261954013157E9
f(x) = (58.19939949943191 * (((-21.597963943138016) + (x - (-45.62170226606368))) * (x * (-3.7782588026154613))))
11 3.545551263086143E9
f(x) = (58.02466439209779 * (((-18.96126891390064) + (x - (-42.781599415004585))) * (x * (-3.7782588026154613))))
12 3.540920767846881E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 5.536053451302263)
13 3.540491873012355E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 24.298797251839378)
14 3.5400393139433427E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 44.48189628414795)
15 3.539557998112941E9
f(x) = ((58.10331852588319 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 70.99484460029008)
16 3.5389568059665136E9
17 3.5389568059665136E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 88.53692878105136)
18 3.5385272071778183E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 96.92101137795909)
19 3.5383341156489058E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 105.50430898480867)
20 3.538137455505746E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 125.68872314958799)
21 3.537679055698119E9
f(x) = ((58.10020017491848 * (((-22.278842813066657) + (x - (-46.17416306325414))) * (x * (-3.7782588026154613)))) - 138.7479712122984)
22 3.5373855115252895E9
23 3.5373855115252895E9
24 3.5373855115252895E9
f(x) = (((-37.26846869977584) * ((x + (x - (-47.687763156745156))) * (x * 2.9419052064299054))) - 176.3754379310957)
25 3.536888676374473E9
f(x) = (((x - (-42.26809684868709)) * (((-22.699862676766646) + (x - (-54.323525268738656))) * (x * 1.2876877679231686))) - ((x * (-13.189341913068064)) * (x * (-9.07445805933937))))
26 3.723766513965906E8
f(x) = ((x * (((-20.77021403281741) + (x - (-56.18018484917877))) * (x * 1.0283534934943348))) - ((x * (-11.462695291605907)) * (x * (-9.07445805933937))))
27 4.193009086099604E7
f(x) = ((x * (((-14.927298962277831) + (x - (-50.217089356831124))) * (x * 0.9988515080579701))) - ((x * (-11.316119006918044)) * (x * (-9.307946228589318))))
28 165047.1068965982
f(x) = ((x * (((-19.126382675050188) + (x - (-50.87926661591404))) * (x * 0.9988515080579701))) - ((x * (-8.677352568505196)) * (x * (-11.734135145640401))))
29 70990.23190410846
f(x) = ((x * (((-16.077554143794146) + (x - (-51.46683847282147))) * (x / 0.9988515080579701))) - ((x * (-11.316119006918044)) * (x * (-9.307946228589318))))
30 66206.62977395783
31 66206.62977395783
32 66206.62977395783
f(x) = ((x * (x * (x + 4.4098695807404145))) - ((x * (-8.78805432781831)) * (x * (-8.466132722703005))))
33 20600.857640909722
f(x) = ((x * (((-16.028672342886313) + (x - (-52.26304159953027))) * x)) - ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
34 806.193032661867
35 806.193032661867
36 806.193032661867
37 806.193032661867
38 806.193032661867
39 806.193032661867
f(x) = ((x * (((-16.028672342886313) + (x - (-52.26296484877049))) * x)) - ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
40 738.4432450889834
41 738.4432450889834
f(x) = ((x * (((-16.00645087483127) + x) * x)) - ((x * (-8.100439392530896)) * (x * (-6.665549678910843))))
42 27.826212573181493
f(x) = ((x * (((-13.242522576569776) + (x - (-49.47522269762757))) * x)) - ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
43 3.528531101472191
Best function is:
f(x) = ((x * (((-13.242522576569776) + (x - (-49.47522269762757))) * x)) - ((x * (-11.740960627643991)) * (x * (-9.048031523291307))))
End time is: Thu Dec 20 05:43:02 EET 2012
Всякий раз, когда я вижу попытки применять генетическое программирование к поиску математических формул, у меня возникают вопросы, на которые пока не нашел ответа, а докладчики мялись и не телились (может, не повезло пока):
— часто применяющие генетическое программирование не догадываются о существовании функции simplify() в почти каждой системе компьютерной алгебры. Один такой персонаж на докладе как-то сокрушался, что у него случается code bloat очевидно сокращаемых выражений, но технологии сокращения у него не было.
— всякую формулу можно переписать в эквивалентном символьном представлении: например, добавить и тут же вычесть некое выражение, а потом скобки переставить. Это наверняка заспамливает пространство случайного поиска, нет? Иными словами, у меня есть сильное подозрение, что генетическое программирование себя хуже ведет в применении к символьным математическим выражениям, чем к иным областям, где «классы эквивалентности» (как угодно определенные) меньше. Вы с этим как-то явно боретесь?
— отдельный случай предыдущего вопроса. Если разрешать вычислять аналитические функции только от мономов, а связывать их арифметическими операциями (чтоб исключить случай вроде \sqrt{x+y}), то цепочку последовательных делений (подходящую дробь) можно привести к нормальному виду (отношению двух выражений полиномиального вида). Таким образом поиск всякого выражения с делением в алфавите можно свести к поиску рациональной функции с заранее неизвестными степенями полиномов в числителе и знаменателе. С точки зрения качества приближения, искать рациональную функцию определенной степени числителя и знаменателя заведомо выгоднее, чем априори произвольное выражение, которое уже затем эквивалентно некоторой рациональной функции. И уж раз вы решаете задачу регрессии, то вычислительно дешевле рациональное приближение, аппроксимирующее тот же корень. Что на этот счет говорит мега-теория генетического программирования?
— часто применяющие генетическое программирование не догадываются о существовании функции simplify() в почти каждой системе компьютерной алгебры. Один такой персонаж на докладе как-то сокрушался, что у него случается code bloat очевидно сокращаемых выражений, но технологии сокращения у него не было.
— всякую формулу можно переписать в эквивалентном символьном представлении: например, добавить и тут же вычесть некое выражение, а потом скобки переставить. Это наверняка заспамливает пространство случайного поиска, нет? Иными словами, у меня есть сильное подозрение, что генетическое программирование себя хуже ведет в применении к символьным математическим выражениям, чем к иным областям, где «классы эквивалентности» (как угодно определенные) меньше. Вы с этим как-то явно боретесь?
— отдельный случай предыдущего вопроса. Если разрешать вычислять аналитические функции только от мономов, а связывать их арифметическими операциями (чтоб исключить случай вроде \sqrt{x+y}), то цепочку последовательных делений (подходящую дробь) можно привести к нормальному виду (отношению двух выражений полиномиального вида). Таким образом поиск всякого выражения с делением в алфавите можно свести к поиску рациональной функции с заранее неизвестными степенями полиномов в числителе и знаменателе. С точки зрения качества приближения, искать рациональную функцию определенной степени числителя и знаменателя заведомо выгоднее, чем априори произвольное выражение, которое уже затем эквивалентно некоторой рациональной функции. И уж раз вы решаете задачу регрессии, то вычислительно дешевле рациональное приближение, аппроксимирующее тот же корень. Что на этот счет говорит мега-теория генетического программирования?
Ваши наблюдения верны: найденные решения могут быть правильными или очень хорошими, но из-за способа построения могут выглядеть довольно громоздко, или содержать мёртвые участки кода. Но вот с Вашими с выводами я не соглашаюсь.
Можно конструировать «простые программы», но во многих случаях это лишь затруднит поиск хорошего решения.
Пример, когда мёртвые участки кода полезны:
представте что мы ищем формулу (1 + (x — 5)^2).
Она может получится в результате мутации дерева с мёртвым участком:
(1 + (x — x)^2) -> (1 + (x — 5)^2)
Можно конструировать «простые программы», но во многих случаях это лишь затруднит поиск хорошего решения.
Пример, когда мёртвые участки кода полезны:
представте что мы ищем формулу (1 + (x — 5)^2).
Она может получится в результате мутации дерева с мёртвым участком:
(1 + (x — x)^2) -> (1 + (x — 5)^2)
ОК, значит мертвые участки кода помогают. Но как часто? Можно ли построить какую-то статистику, доказывающую на (пусть игрушечном) примере, что допускать мертвый код выгоднее (быстрее сойдемся), чем добавлять случайные ветки к формулам без мертвых участков?
сюда же вопрос: вы сами пишете об оптимизациях, фактически — частичных упрощениях формул. Ваши оптимизации могут значительно изменять синтаксическое дерево формулы. Как быть с предполагаемой гладкостью пространства поиска? Наивно рассуждая, тут либо нужно бороться за гладкость, либо решительно все упрощать. Но во втором случае может есть смысл пойти еще дальше и ограничить класс функций-приближений, например, рациональными.
На самом деле, оптимизации, которые я описал, можно разбить на две группы:
- Оптимизации, ускоряющие поиск решения:
- Оптимизация коэффициентов деревьев (без изменения структуры дерева)
- Добавление случайных деревьев в популяцию, в случае, если генетический алгоритм застрял в локальном минимуме
- Оптимизация коэффициентов деревьев (без изменения структуры дерева)
- Оптимизации, что упрощают структуру дерева, на самом деле реализованы из чисто практических соображений, чтоб контролировать расходы памяти
— всякую формулу можно переписать в эквивалентном символьном представлении: например, добавить и тут же вычесть некое выражение, а потом скобки переставить. Это наверняка заспамливает пространство случайного поиска, нет? Иными словами, у меня есть сильное подозрение, что генетическое программирование себя хуже ведет в применении к символьным математическим выражениям, чем к иным областям, где «классы эквивалентности» (как угодно определенные) меньше. Вы с этим как-то явно боретесь?
Эти лишние дубликаты «генов» очень полезны при мутациях — потому что однажды образовавшись, дальше каждый из дублей получает возможность мутировать независимо, и таким образом обнаруживать решения, без наличия дубля изначально недостижимые.
Посему simplify можно применять изредка, на случайных шагах мутогенеза, или даже лишь в конце — но никак не после каждого шага.
о том, что дубликаты генов полезны я уже много раз слышал, но сам я с генетическим программированием не игрался (в отличие от компьютерной алгебры), поэтому мне трудно в это поверить на слово. Потому всем и всегда задаю вопрос: откуда следует, что эти дубликаты полезнее, чем альтернативные способы организации поиска? Примеры альтернатив: часто добавлять случайные поддеревья (может быть эквивалентно мутациям в «мертвом коде»), забить на формулировки генетического программирования и искать рациальных аппроксимаций. Кто-нибудь этот вопрос исследовал? Спрашиваю не чтоб подколоть, мне правда интересен ответ. Потому что априори генетическое программирование в применении к математическим выражениям для меня (математика по образованию, плотно работавшему с компьютерной алгеброй) выглядит псевдонаучной магией.
Просто про дубликаты генов речь чаще в биологии идёт, там где практически нет генератора случайных последовательностей ДНК, но есть дубликаторы кусочков и мелкие изменения в существующих последовательностях.
И там основной бонус заключался в том, что когда ген в ДНК дублировался — его функция не нарушалась, и вторая копия могла мутировать без ущерба для организма, и в результате иногда приводила к образованию новых возможностей. И когда после этого вдруг ломалась первая копия, генотип не подыхал, а начинал жить несколько иначе.
Возможно, будь у эволюции эффективный способ генерить случайные поддеревья или искать рациональные аппроксимации (а это, похоже, руками генетиков у эволюции скоро образуется) — то эволюция пойдёт целенаправленнее. Там где можно взять и посчитать, гадание на кофейной гуже или методом монте-карло действительно не всегда эффективно… Тут выбор между угадать, перебрать всё или посчитать. Иногда второе слишком долго, последнее просто тупо сложнее или вовсе не придумано, а угадать вполне реально…
И там основной бонус заключался в том, что когда ген в ДНК дублировался — его функция не нарушалась, и вторая копия могла мутировать без ущерба для организма, и в результате иногда приводила к образованию новых возможностей. И когда после этого вдруг ломалась первая копия, генотип не подыхал, а начинал жить несколько иначе.
Возможно, будь у эволюции эффективный способ генерить случайные поддеревья или искать рациональные аппроксимации (а это, похоже, руками генетиков у эволюции скоро образуется) — то эволюция пойдёт целенаправленнее. Там где можно взять и посчитать, гадание на кофейной гуже или методом монте-карло действительно не всегда эффективно… Тут выбор между угадать, перебрать всё или посчитать. Иногда второе слишком долго, последнее просто тупо сложнее или вовсе не придумано, а угадать вполне реально…
По первому вопросу — упрощение иногда используется (оператор edit) но обычно неэффективно.
Его есть смысл использовать когда результат уже получен и его надо упростить.
Кроме того часто используется parsimony pressure — добавление в фитнесс-функцию пенальти на сложность.
Ну и есть еще методы, прямо учитывающие MDL.
Отдельный вопрос — добро или зло code bloat
Иногда специально вставляют в исходный набор функций возможность формирования интронов.
Считается (но обоснований я не встречал), что в интронах накапливается генетический материал для скачкообразной макроэволюции.
Т.е. там хранятся последовательности, которые где-то когда-то пригодились, но пока не нужны и могут выстрелить позже.
По второму вопросу — даже введение дополнительных функций начинает сильно тормозить процесс, например если мы ищем полином, но добавили тригонометрию — сходимость падает, за счет ложных приближенных решений.
Но тут зависит от ландшафта.
Нам надо найти один единственный пример из многих классов эквивалентности.
И чем больше этот класс — тем больше вероятность его нахождения по разным траекториям.
Вообще попытки задать однозначное представление и свести классы эквивалентности к одному единственному экземпляру сразу снижают сходимость.
Это все однако не теория, а просто мой личный опыт использования таких систем.
Следует еще понимать, что для сложных задач ГП не проводит разделения пространства на независимые компоненты (хотя было много попыток в этом направлении, те же ADF или применение eCGA из ГА-мира).
И потому сходимость на очень сложных задачах плохая и сами задачи решать крайне затратно.
Кто сможет обойти это ограничение — получит большой приз.
Его есть смысл использовать когда результат уже получен и его надо упростить.
Кроме того часто используется parsimony pressure — добавление в фитнесс-функцию пенальти на сложность.
Ну и есть еще методы, прямо учитывающие MDL.
Отдельный вопрос — добро или зло code bloat
Иногда специально вставляют в исходный набор функций возможность формирования интронов.
Считается (но обоснований я не встречал), что в интронах накапливается генетический материал для скачкообразной макроэволюции.
Т.е. там хранятся последовательности, которые где-то когда-то пригодились, но пока не нужны и могут выстрелить позже.
По второму вопросу — даже введение дополнительных функций начинает сильно тормозить процесс, например если мы ищем полином, но добавили тригонометрию — сходимость падает, за счет ложных приближенных решений.
Но тут зависит от ландшафта.
Нам надо найти один единственный пример из многих классов эквивалентности.
И чем больше этот класс — тем больше вероятность его нахождения по разным траекториям.
Вообще попытки задать однозначное представление и свести классы эквивалентности к одному единственному экземпляру сразу снижают сходимость.
Это все однако не теория, а просто мой личный опыт использования таких систем.
Следует еще понимать, что для сложных задач ГП не проводит разделения пространства на независимые компоненты (хотя было много попыток в этом направлении, те же ADF или применение eCGA из ГА-мира).
И потому сходимость на очень сложных задачах плохая и сами задачи решать крайне затратно.
Кто сможет обойти это ограничение — получит большой приз.
о! Похоже это тот камент, которого я искал.
Крайне контр-интуитивно то, что, по вашим словам, чем больше эквивалентных представлений мы допускаем, тем больше вероятность сойтись быстрее. И кажется, вы слегка себе противоречите, добавляя про ухудшение сходимости при добавлении дополнительных функций. Ведь дополнительные функции только расширяют класс эквивалентности? :)
Не могли бы вы дать пример, когда вы в реальной задаче использовали ГП? У меня таких задач не было, вот и пытаюсь отделить мух от котлет.
Крайне контр-интуитивно то, что, по вашим словам, чем больше эквивалентных представлений мы допускаем, тем больше вероятность сойтись быстрее. И кажется, вы слегка себе противоречите, добавляя про ухудшение сходимости при добавлении дополнительных функций. Ведь дополнительные функции только расширяют класс эквивалентности? :)
Не могли бы вы дать пример, когда вы в реальной задаче использовали ГП? У меня таких задач не было, вот и пытаюсь отделить мух от котлет.
Это действительно интересный вопрос.
Если классы эквивалентности вырождены, то на экстремум ведет один единственный путь. Поэтому в таких случаях сходимость тяжелая.
Можно сказать, что ГП использует обобщенный вариант «атаки дней рождения» — стыкуя отдельные блоки.
Но если классы эквивалентности большие, то это еще ничего не значит.
В случае допустим добавления тригонометрии ГП начинает искать приближенные решения там, где есть точные и такие функции «отравляют» пространство поиска и сильно увеличивают его.
Поэтому я делаю обычно так — выбираю минимальный базис при широких правилах конструирования, так чтобы информация больше кодировалась в связях и перестановках, а не в единицах генома.
И кстати STGP (strongly type GP) лучше сходится.
Вообще теория ГП обычно останавливается на аналоге теоремы шим, которая говорит, что да, при сферических условиях в ваккуме алгоритм сходится максимум экспоненциально. Ну еще понятие эффективного фитнесса есть, но как его считать — не всегда ясно.
Хотя там очень много дополнительных условий, например термин «катастрофа ошибок», который знают биологи, в ГП я никогда не встречал.
Соответственно рулит голая эмпирика, что не может не сказываться на результатах.
Я использовал ГП много раз, в конце 90-х для торговых роботов, это было первое мое использование, но это были конечно игрушки, хотя и рабочие. Накатал свой вариант с блекджеком и шлюхами на С, наигрался.
Из последних (хотя там ближе к grammatical evolution — GE варианту — линейный геном на произвольной грамматике) вот например классификаторы малвари в форме decision tree были года три назад.
Интересно что на небольших сетах (4-5К) получившийся классификатор заруливал и CART и SVM.
Но как только сет начинал расти — все, качество падало или требовало огромных вычислительных ресурсов за счет уменьшения сходимости.
Использовал GP для набора рандомных атрибутов под decision tree классификаторы, очень неплохо выходило, но сильно долго, и много дубликатов получалось, а хорошую фитнесс функцию, учитывающую mutual information всех предыдущих атрибутов так и не удалось создать.
Ну и для генерации тестовых последовательностей использовал, типа фаззера или автоматического тестирования — перенаправляю вывод на вход тестируемой программы и запускаю все под valgrind'ом на недельку.
Потом смотрю логи, где упало или память утекла.
Но это тоже больше к GE уже относится.
Вообще имхо GP хорош когда надо найти приближенное приемлимое решение. По мере приближения к глобальному оптимуму сходимость падает и доводить до конца не всегда есть смысл.
Ну и есть интересное применение, когда фитнесс-функции не существует аналитически, например когда полезность определяется лайками пользователей.
Т.е. робот генерирует варианты решений, а люди их оценивают.
Сейчас я делаю свой вариант, который использует GP/GE частично, но основой является скорее GMDH схема, это работает пока только на классификаторах.
Но тут подробнее рассказать не могу — не исключено что будет реальный патент.
Если классы эквивалентности вырождены, то на экстремум ведет один единственный путь. Поэтому в таких случаях сходимость тяжелая.
Можно сказать, что ГП использует обобщенный вариант «атаки дней рождения» — стыкуя отдельные блоки.
Но если классы эквивалентности большие, то это еще ничего не значит.
В случае допустим добавления тригонометрии ГП начинает искать приближенные решения там, где есть точные и такие функции «отравляют» пространство поиска и сильно увеличивают его.
Поэтому я делаю обычно так — выбираю минимальный базис при широких правилах конструирования, так чтобы информация больше кодировалась в связях и перестановках, а не в единицах генома.
И кстати STGP (strongly type GP) лучше сходится.
Вообще теория ГП обычно останавливается на аналоге теоремы шим, которая говорит, что да, при сферических условиях в ваккуме алгоритм сходится максимум экспоненциально. Ну еще понятие эффективного фитнесса есть, но как его считать — не всегда ясно.
Хотя там очень много дополнительных условий, например термин «катастрофа ошибок», который знают биологи, в ГП я никогда не встречал.
Соответственно рулит голая эмпирика, что не может не сказываться на результатах.
Я использовал ГП много раз, в конце 90-х для торговых роботов, это было первое мое использование, но это были конечно игрушки, хотя и рабочие. Накатал свой вариант с блекджеком и шлюхами на С, наигрался.
Из последних (хотя там ближе к grammatical evolution — GE варианту — линейный геном на произвольной грамматике) вот например классификаторы малвари в форме decision tree были года три назад.
Интересно что на небольших сетах (4-5К) получившийся классификатор заруливал и CART и SVM.
Но как только сет начинал расти — все, качество падало или требовало огромных вычислительных ресурсов за счет уменьшения сходимости.
Использовал GP для набора рандомных атрибутов под decision tree классификаторы, очень неплохо выходило, но сильно долго, и много дубликатов получалось, а хорошую фитнесс функцию, учитывающую mutual information всех предыдущих атрибутов так и не удалось создать.
Ну и для генерации тестовых последовательностей использовал, типа фаззера или автоматического тестирования — перенаправляю вывод на вход тестируемой программы и запускаю все под valgrind'ом на недельку.
Потом смотрю логи, где упало или память утекла.
Но это тоже больше к GE уже относится.
Вообще имхо GP хорош когда надо найти приближенное приемлимое решение. По мере приближения к глобальному оптимуму сходимость падает и доводить до конца не всегда есть смысл.
Ну и есть интересное применение, когда фитнесс-функции не существует аналитически, например когда полезность определяется лайками пользователей.
Т.е. робот генерирует варианты решений, а люди их оценивают.
Сейчас я делаю свой вариант, который использует GP/GE частично, но основой является скорее GMDH схема, это работает пока только на классификаторах.
Но тут подробнее рассказать не могу — не исключено что будет реальный патент.
Спасибо за развернутый и очень полезный ответ. Крайне поучительно узнать, с какими задачами сталкиваются в параллельной реальности :) Еще ваш ответ мне напомнил деятельность хабраюзера TheShade, который таким способом искал (а может и продолжает искать) оптимальные настройки Java-машин.
Конкретно про регрессию — лично для меня выстрелил ваш ответ про то, что тригонометрические функции аппроксимируют приближенно там, где можно точно.
И еще очень поучительно про катастрофу ошибок.
А вы не встречали случаем сравнений ГП (в широком смысле) с монте-карлой с марковскими цепями, алгоритм Метрополиса? Интуитивно кажется, что это все про одно и то же, только язык разный. И в отличие от ГП, для марковских цепей тут недавно некая группа исследователей продвигала идею настраивать вероятности перехода в цепи маркова так, чтобы в итоге монте-карла сходилась не просто так, а бежала по геодезической (!) в соответствующем многообразии вероятностной меры. До конца я их идею не понял, но общего образования хватает, чтоб понять: вместо поиска, направленного как-то, они предлагают выбирать преимущественное направление следущего шага так, что он в среднем бежал к оптимуму по кратчайшему пути. Если интересно, попробую вспомнить/найти ключевые слова для поиска.
Конкретно про регрессию — лично для меня выстрелил ваш ответ про то, что тригонометрические функции аппроксимируют приближенно там, где можно точно.
И еще очень поучительно про катастрофу ошибок.
А вы не встречали случаем сравнений ГП (в широком смысле) с монте-карлой с марковскими цепями, алгоритм Метрополиса? Интуитивно кажется, что это все про одно и то же, только язык разный. И в отличие от ГП, для марковских цепей тут недавно некая группа исследователей продвигала идею настраивать вероятности перехода в цепи маркова так, чтобы в итоге монте-карла сходилась не просто так, а бежала по геодезической (!) в соответствующем многообразии вероятностной меры. До конца я их идею не понял, но общего образования хватает, чтоб понять: вместо поиска, направленного как-то, они предлагают выбирать преимущественное направление следущего шага так, что он в среднем бежал к оптимуму по кратчайшему пути. Если интересно, попробую вспомнить/найти ключевые слова для поиска.
Я встречал например выбор алгоритма кеширования на реальных данных путем ГП.
Сам похожи почти не занимался, обычно структура более или менее понятна, а робастность решений найденных ГП часто под вопросом.
По поводу Монте-Карло, я могу сказать, что я сравнивал, ГА/ГП лучше практически всегда.
Я рассматриваю ГА — как МК с улучшенной сходимостью (благодаря теореме шим).
А ГП — как ГА в тьюринговски полном пространстве.
Это достаточно условная иерархия, особенно если учесть большое количество модификаций этих алгоритмов.
С Марковскими моделями, как и с Байесовскими сетями есть одна проблема.
Они отлично работают если они уже построены.
:-)
А строить их автоматизированной процедурой обычно достаточно затратно на реальных данных, не говоря уже о BigData. Т.е. понятно что если это полный связный граф, в вырожденных случаях например дерева или линейного графа строится нормально.
То, что я видел реально работающего было обычно достаточно убого и строилось с учетом экспертных мнений, здравого смысла и других вариантов генератора случайных чисел.
Априорное знание — страшная вещь.
:-)
Собственно поэтому я с такими моделями практически и не работал, ну там Chou-Liu дерево максимум сделаю, так и то, CART часто давал лучшую аппроксимацию.
Вот кстати на старой винде их экспертная система помощи так работает — и что-то я мало встречал кому эта помощь помогла.
Плюс был опыт когда мой тупейший алгоритм на базе полунаивного Байеса скрещенного с бубном побил тщательно спроектированную HMM.
Роль бубна правда осталась неясна.
:-)
Хотя специально курс PGM прошел — чтобы проверить, может я что-то не понимаю, вроде популярная техника.
Но имхо в генетике проблема не в этом.
Сходится она достаточно неплохо для серебряной пули.
Но если бы она могла эффективно делать декомпозицию пространства поиска на декартово произведение — уменьшая тем самым сложность — вот это было бы то, что надо.
И если бы она могла выделять и сохранять крупные структурные блоки для последующего использования — это тоже было бы отлично.
Сложный блок имеет больше вероятности развалиться при мутации или кроссовере.
И воэтому при приближении к решению — скорость падает, причем экспоненциально.
Я решал это «перенормировкой», выделением случайных блоков из особо успешных программ как новых генов.
Но решалось плохо и уже серебряной пулей не было.
Хотя возможно там есть еще потенциал.
Лет десять назад это было модно — искать такие расширения ГП.
Сейчас вроде поутихло.
PS
Варианты ГП кстати в проектировании железа очень часто используют.
Но там есть т.н. cartesian genetic programming, такой комбинаторный вариант.
Версий ГП вообще over 9000.
Сам похожи почти не занимался, обычно структура более или менее понятна, а робастность решений найденных ГП часто под вопросом.
По поводу Монте-Карло, я могу сказать, что я сравнивал, ГА/ГП лучше практически всегда.
Я рассматриваю ГА — как МК с улучшенной сходимостью (благодаря теореме шим).
А ГП — как ГА в тьюринговски полном пространстве.
Это достаточно условная иерархия, особенно если учесть большое количество модификаций этих алгоритмов.
С Марковскими моделями, как и с Байесовскими сетями есть одна проблема.
Они отлично работают если они уже построены.
:-)
А строить их автоматизированной процедурой обычно достаточно затратно на реальных данных, не говоря уже о BigData. Т.е. понятно что если это полный связный граф, в вырожденных случаях например дерева или линейного графа строится нормально.
То, что я видел реально работающего было обычно достаточно убого и строилось с учетом экспертных мнений, здравого смысла и других вариантов генератора случайных чисел.
Априорное знание — страшная вещь.
:-)
Собственно поэтому я с такими моделями практически и не работал, ну там Chou-Liu дерево максимум сделаю, так и то, CART часто давал лучшую аппроксимацию.
Вот кстати на старой винде их экспертная система помощи так работает — и что-то я мало встречал кому эта помощь помогла.
Плюс был опыт когда мой тупейший алгоритм на базе полунаивного Байеса скрещенного с бубном побил тщательно спроектированную HMM.
Роль бубна правда осталась неясна.
:-)
Хотя специально курс PGM прошел — чтобы проверить, может я что-то не понимаю, вроде популярная техника.
Но имхо в генетике проблема не в этом.
Сходится она достаточно неплохо для серебряной пули.
Но если бы она могла эффективно делать декомпозицию пространства поиска на декартово произведение — уменьшая тем самым сложность — вот это было бы то, что надо.
И если бы она могла выделять и сохранять крупные структурные блоки для последующего использования — это тоже было бы отлично.
Сложный блок имеет больше вероятности развалиться при мутации или кроссовере.
И воэтому при приближении к решению — скорость падает, причем экспоненциально.
Я решал это «перенормировкой», выделением случайных блоков из особо успешных программ как новых генов.
Но решалось плохо и уже серебряной пулей не было.
Хотя возможно там есть еще потенциал.
Лет десять назад это было модно — искать такие расширения ГП.
Сейчас вроде поутихло.
PS
Варианты ГП кстати в проектировании железа очень часто используют.
Но там есть т.н. cartesian genetic programming, такой комбинаторный вариант.
Версий ГП вообще over 9000.
Решение методом Монте-Карло, сходящееся куда-то — это ж и есть ГА, насколько я понимаю.
А сам по себе метод Монте-Карло вроде же никуда не сходится, просто случайно пространство аргументов прочёсывает. Разве нет?
А сам по себе метод Монте-Карло вроде же никуда не сходится, просто случайно пространство аргументов прочёсывает. Разве нет?
ну да, и останавливается когда найдет.
ГА делает тоже самое, но быстрее.
ГА ищет более «разумно», оно включает в себя локальные изменения (мутации) и дальние прыжки — кроссовер.
А так — то же самое, случайный поиск.
Поэтому ГА и является «серебряной пулей».
Ну или почти серебряной.
ГА делает тоже самое, но быстрее.
ГА ищет более «разумно», оно включает в себя локальные изменения (мутации) и дальние прыжки — кроссовер.
А так — то же самое, случайный поиск.
Поэтому ГА и является «серебряной пулей».
Ну или почти серебряной.
Ну, тут вопрос в определении того, что такое монте-карло. Если просто лепим много случайных нескоррелированных вариантов и проверяем какой лучше, то да, все как вы и говорите. Сам никуда не сходится, но по теореме Пуанкаре, рано или поздно пройдет рядом с нужной точкой.
Но так называемые Markov Chain Monte Carlo алгоритмы лепят случайные значения не с равной вероятностью. У них марковская цепь отвечает за выбор преимущественного направления так, чтоб процесс при этом оставался случайным. Ключевые слова — алгоритм метрополиса. Исходно оно было придумано в стат. физике — там все пространство состояний не обойдешь, но физический смысл несут только некоторые точки пространства состояний, причем заранее неясно, какие.
Но так называемые Markov Chain Monte Carlo алгоритмы лепят случайные значения не с равной вероятностью. У них марковская цепь отвечает за выбор преимущественного направления так, чтоб процесс при этом оставался случайным. Ключевые слова — алгоритм метрополиса. Исходно оно было придумано в стат. физике — там все пространство состояний не обойдешь, но физический смысл несут только некоторые точки пространства состояний, причем заранее неясно, какие.
Не дописал. Ключевое в этой идее — вместо того, чтоб притягивать за уши биологическую аналогию и уже потом вставлять туда костыли типа «а мы придумали новое правило мутации так, чтоб у нас вот тут лучше сходилось, мы проверили», люди рассуждают в терминах чистой теории вероятности: нам надо бежать по пространству, как не знаем, но пусть пробные точки вынимаются из некоторого распределения вероятностей — вот это распределение мы подкручивать и будем. а уже за это отвечает цепь маркова, веса перехода из состояний в состояние у которой можно на ходу прокручивать, так что она «учится», а в немаркетинговых терминах — мы имеем последовательность распределение вероятности таких, что они в конце концов сходятся к правильному (но заранее не известному). Мне моя интуиция говорит, что такая модель более или менее эквивалентна ГП, но «честнее» ее, не приносит лишней мишуры и сразу обнажает объект, над которым работаем.
Те гаврики, о которых я писал чуть выше, придумали как работать не просто с последовательностями распределение вероятности, про которые ничего не известно, а обнаружили там богатую дифференциальную геометрию и сказали, как можно сходиться к правильному (но заранее неизвестному) распределению по кратчайшему пути в неком пространстве всяких распределений.
Те гаврики, о которых я писал чуть выше, придумали как работать не просто с последовательностями распределение вероятности, про которые ничего не известно, а обнаружили там богатую дифференциальную геометрию и сказали, как можно сходиться к правильному (но заранее неизвестному) распределению по кратчайшему пути в неком пространстве всяких распределений.
Я имел в виду конечно классический МC, с запоминанием лучшего результата, не MCMC.
Со статфизикой не все так просто.
В статфизике другой подход — постулируемая неизмеримость микроскопических состояний и поиск макроскопических значений.
В типовых задачах ИИ проблема обычно ставится по другому.
Это не исключает использование методов физики в ИИ (тот же Simulated Annealing), но задачи все-таки не пересекаются.
И не забываем, что ни статфизика ни неравновесная термодинамика не так хорошо описывают процессы в живых системах, как нам бы хотелось.
С другой стороны методы статфизики достаточно обоснованы и математизированы, а метаэвристический инструментарий — это эмпирика в чистом виде.
Поэтому использование метаэвристик всегда несет в себе некоторый риск.
По поводу MCMC — есть много моделей, которые «честнее», но все они несут в себе некоторые неявные предположения о структуре функции распределения вероятностей.
В отличие от ГА, хотя разумеется можно найти специальные ландшафты, где он будет мягко говоря неэффективен при специально подобранных параметрах.
Но обычная ситуация — десятки тысяч измерений, мультимодальное распределение о котором известно лишь то, что оно очень сложное и имеет миллионы локальных экстремумов.
Если мы говорим об MH алгоритме, то с гауссовым начальным распределением он дает очень маленькую вероятность больших скачков по сравнению с ГА и следовательно имеет больше шансов попасть в локальный экстремум.
Если же мы говорим об MCMC вообще — то он не накапливает информацию о сложных связях и о истории поиска (для чего в ГА нужны интроны) — потому он и Марковский.
Скорость накопления информации в ГА достигает экспоненциальной. Это верхняя граница и она определена schemata theorem.
Для MCMC, насколько я понимаю, такая скорость возможна лишь в очень специфичных условиях.
ГА мне до близкого знакомства казались шаманством чистой воды, попыткой списать код у бога, вырвав страницу из исходников, без особого понимания смысла. Особенно если учесть мой крайне неудачный на то время опыт работы с еще одной попыткой списывания — нейронными сетями.
И после некоторых тестовых применений мнение мое не изменилось.
Я например пытался решить задачу плотного размещения UML-графа на плоскости — не то, чтобы не работало, но, дорого, глупо и не гарантирует результат.
Но когда разобрался, и очертил границы применения — то понял, что метод вполне рабочий.
Просто это наиболее близкая штука к тому, что называется «серебряной пулей», а в соответствии с теоремой NFL серебряные пули обычно или стоят дорого или кучность плохая или можно прострелить себе ногу очень странным и неожиданным образом.
:-)
ГП кстати обладает некоторыми человеческими свойствами — он часто бывает лжив и ленив и ловит программиста на ошибках.
:-)
Рассмотрим простую проблему — слева набор прямоугольников, справа набор эллипсов, найти процедуру, отличающую первые от вторых.
Нейронки или SVM построят сложную модель, которая что-то будет делать.
ГП ответит просто, правильно и неожиданно — основным отличием является то слева или справа находится фигура.
:-)
ГП использует неожидаемые или неявные зависимости, которые программист может просто не заметить в постановке или в обычном для нашей индустрии упрощении.
В этом качестве я использую его наиболее часто.
Исследовать пространство поиска например, чтобы затем уже найти более оптимальную процедуру.
Получить наиболее адекватный набор атрибутов для текста или картинки.
А дальше можно и специальные методы применять, быстрые и предсказуемые.
Должен же где-то у программиста лежать бубен…
:-)
Со статфизикой не все так просто.
В статфизике другой подход — постулируемая неизмеримость микроскопических состояний и поиск макроскопических значений.
В типовых задачах ИИ проблема обычно ставится по другому.
Это не исключает использование методов физики в ИИ (тот же Simulated Annealing), но задачи все-таки не пересекаются.
И не забываем, что ни статфизика ни неравновесная термодинамика не так хорошо описывают процессы в живых системах, как нам бы хотелось.
С другой стороны методы статфизики достаточно обоснованы и математизированы, а метаэвристический инструментарий — это эмпирика в чистом виде.
Поэтому использование метаэвристик всегда несет в себе некоторый риск.
По поводу MCMC — есть много моделей, которые «честнее», но все они несут в себе некоторые неявные предположения о структуре функции распределения вероятностей.
В отличие от ГА, хотя разумеется можно найти специальные ландшафты, где он будет мягко говоря неэффективен при специально подобранных параметрах.
Но обычная ситуация — десятки тысяч измерений, мультимодальное распределение о котором известно лишь то, что оно очень сложное и имеет миллионы локальных экстремумов.
Если мы говорим об MH алгоритме, то с гауссовым начальным распределением он дает очень маленькую вероятность больших скачков по сравнению с ГА и следовательно имеет больше шансов попасть в локальный экстремум.
Если же мы говорим об MCMC вообще — то он не накапливает информацию о сложных связях и о истории поиска (для чего в ГА нужны интроны) — потому он и Марковский.
Скорость накопления информации в ГА достигает экспоненциальной. Это верхняя граница и она определена schemata theorem.
Для MCMC, насколько я понимаю, такая скорость возможна лишь в очень специфичных условиях.
ГА мне до близкого знакомства казались шаманством чистой воды, попыткой списать код у бога, вырвав страницу из исходников, без особого понимания смысла. Особенно если учесть мой крайне неудачный на то время опыт работы с еще одной попыткой списывания — нейронными сетями.
И после некоторых тестовых применений мнение мое не изменилось.
Я например пытался решить задачу плотного размещения UML-графа на плоскости — не то, чтобы не работало, но, дорого, глупо и не гарантирует результат.
Но когда разобрался, и очертил границы применения — то понял, что метод вполне рабочий.
Просто это наиболее близкая штука к тому, что называется «серебряной пулей», а в соответствии с теоремой NFL серебряные пули обычно или стоят дорого или кучность плохая или можно прострелить себе ногу очень странным и неожиданным образом.
:-)
ГП кстати обладает некоторыми человеческими свойствами — он часто бывает лжив и ленив и ловит программиста на ошибках.
:-)
Рассмотрим простую проблему — слева набор прямоугольников, справа набор эллипсов, найти процедуру, отличающую первые от вторых.
Нейронки или SVM построят сложную модель, которая что-то будет делать.
ГП ответит просто, правильно и неожиданно — основным отличием является то слева или справа находится фигура.
:-)
ГП использует неожидаемые или неявные зависимости, которые программист может просто не заметить в постановке или в обычном для нашей индустрии упрощении.
В этом качестве я использую его наиболее часто.
Исследовать пространство поиска например, чтобы затем уже найти более оптимальную процедуру.
Получить наиболее адекватный набор атрибутов для текста или картинки.
А дальше можно и специальные методы применять, быстрые и предсказуемые.
Должен же где-то у программиста лежать бубен…
:-)
Похоже, я нахожусь в той самой стадии, когда круг задач ГП еще не очерчен. Просто опыта не хватает. Потому и кажется скорее шаманством, чем наоборот. Скорее всего, это своего рода неопытность. Ну, может и пригодится еще когда-нибудь.
Я правильно вас понял, что вы ГП используете чуть ли не как способ само-перепроверки техзаданий? :) Что-то вроде проверки решений другим путем у математиков.
Я правильно вас понял, что вы ГП используете чуть ли не как способ само-перепроверки техзаданий? :) Что-то вроде проверки решений другим путем у математиков.
Скорее проверки инструментария и возможного его уточнения.
Вот кстати пример такого подхода в анализе изображений.
cienciascomp.cicese.mx/evovision/olague_EC_MIT.pdf
Т.е. надо определить точки интереса на изображении, обычный программист возьмет openCV и успокоится.
Но если надо шагнуть дальше и глубже — то можно перелопатить литературу и найти разные варианты определения точек интереса.
А можно потратить время и сделать так как в статье — определить какое конкретное решение лучше всего подходит для конкретной задачи.
Вот другой вариант
citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.801
Написать процедуру кеширования на С.
Опять таки, в большинстве случаев все берут LRU, не особо задумываясь.
Но если скорость критична — то вот их решение, полученное GP на их конкретном потоке данных, будет намного лучше.
На другом потоке данных — возможно нет.
Хотя опять таки, как сделать.
Я сейчас как раз с изображениями работаю.
И вот допустим нам надо выделить особые точки и создать дескрипторы.
И на митинге один предлагает DoG, другой — SURF, третий ORB ну, как обычно.
В теории менеджмента один гуру должен встать и выбрать, сказав «да будет так», высосав решение из… скажем так, личного опыта.
Но можно построить грамматику, которая объединяет все предложения, определелить фитнесс-функцию и запустить ГП-поиск по всем вариантам решений, включая производные.
И получить объективный валидный результат, а не продукт, вытащенный из астрала медитирующим руководителем.
В ситуации, когда ложные решения стоят дорого, а область работы в тумане, такой подход сильно облегчает жизнь, несмотря на начальные затраты.
И самое главное, иногда такой подход позволяет наткнуться на неожиданное решение, которые бы при обычной работе осталось незамеченным.
Вот кстати пример такого подхода в анализе изображений.
cienciascomp.cicese.mx/evovision/olague_EC_MIT.pdf
Т.е. надо определить точки интереса на изображении, обычный программист возьмет openCV и успокоится.
Но если надо шагнуть дальше и глубже — то можно перелопатить литературу и найти разные варианты определения точек интереса.
А можно потратить время и сделать так как в статье — определить какое конкретное решение лучше всего подходит для конкретной задачи.
Вот другой вариант
citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.801
Написать процедуру кеширования на С.
Опять таки, в большинстве случаев все берут LRU, не особо задумываясь.
Но если скорость критична — то вот их решение, полученное GP на их конкретном потоке данных, будет намного лучше.
На другом потоке данных — возможно нет.
Хотя опять таки, как сделать.
Я сейчас как раз с изображениями работаю.
И вот допустим нам надо выделить особые точки и создать дескрипторы.
И на митинге один предлагает DoG, другой — SURF, третий ORB ну, как обычно.
В теории менеджмента один гуру должен встать и выбрать, сказав «да будет так», высосав решение из… скажем так, личного опыта.
Но можно построить грамматику, которая объединяет все предложения, определелить фитнесс-функцию и запустить ГП-поиск по всем вариантам решений, включая производные.
И получить объективный валидный результат, а не продукт, вытащенный из астрала медитирующим руководителем.
В ситуации, когда ложные решения стоят дорого, а область работы в тумане, такой подход сильно облегчает жизнь, несмотря на начальные затраты.
И самое главное, иногда такой подход позволяет наткнуться на неожиданное решение, которые бы при обычной работе осталось незамеченным.
В некоторм роде вы говорите правильные вещи, но ваш стиль комментирования довольно предвзятый (я имею ввиду выражения «притягивать за уши», «костыли», «мега-теория» и т.п.)
Тем более, вы тоже оперируете далеко не академически точными понятиями и терминами.
Как человек с образованием в данной области (квантовая механика и стат. термодинамика), хочу обратить внимание на то, что вы заблуждаетесь относительно того, что "… физический смысл имеют только некоторые точки пространства состояний, причем заранее неясно, какие..." — физический смысл имеют все точки фазового пространства, и он чётко определяется в терминах классической термодинамики.
Второе замечание, — задачи о которых вы упоминаете довольно легко поддаются сферическо-вакуумному формализму. Поэтому, если вы попытаетесь методами чистой стат. физики, например, рассчитать теплоемкость реального кристалла (какого-нибудь германия), или рассчитать температуру фазового равновесия (даже простой воды), то вы потерпите эпический крах — получите результаты, которые могут на порядки отличатся от реальных измерений (почему? да, как минимум, потому что невозможно аналитически рассчитать интеграл взаимодействия в системе, которая содержит больше одного электрона). А для практических расчётов, всё так же, используются всяческие приближения и эмпирические модели.
И да, признаюсь, я тоже не в восторге от обилия биологических терминов в литературе по генетическим алгоритмам, но, во-первых, вы могли заметить что я без надобности не злоупотребляю таковыми. А во-вторых, хоть данные алгоритмы ещё на стадии эмпирических исследований, но это совсем не отменяет того факта, что они позволяют получать хорошие решения.
Последняя аналогия — классическая термодинамика, как область естествознания, полностью построена на эмпирике. Хочу привести цитату А. Эйнштейна* по этому поводу: «Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область её применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная физическая теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута (к особому сведению принципиальных скептиков)» — не замечаете ли аналогии?
* (Цит. по: Кириллин Б. Л., Сычев В. В., Шейндлин А. Е. Техническая термодинамика, 3-е изд. М., 1979, с. 502.)
Тем более, вы тоже оперируете далеко не академически точными понятиями и терминами.
Как человек с образованием в данной области (квантовая механика и стат. термодинамика), хочу обратить внимание на то, что вы заблуждаетесь относительно того, что "… физический смысл имеют только некоторые точки пространства состояний, причем заранее неясно, какие..." — физический смысл имеют все точки фазового пространства, и он чётко определяется в терминах классической термодинамики.
Второе замечание, — задачи о которых вы упоминаете довольно легко поддаются сферическо-вакуумному формализму. Поэтому, если вы попытаетесь методами чистой стат. физики, например, рассчитать теплоемкость реального кристалла (какого-нибудь германия), или рассчитать температуру фазового равновесия (даже простой воды), то вы потерпите эпический крах — получите результаты, которые могут на порядки отличатся от реальных измерений (почему? да, как минимум, потому что невозможно аналитически рассчитать интеграл взаимодействия в системе, которая содержит больше одного электрона). А для практических расчётов, всё так же, используются всяческие приближения и эмпирические модели.
И да, признаюсь, я тоже не в восторге от обилия биологических терминов в литературе по генетическим алгоритмам, но, во-первых, вы могли заметить что я без надобности не злоупотребляю таковыми. А во-вторых, хоть данные алгоритмы ещё на стадии эмпирических исследований, но это совсем не отменяет того факта, что они позволяют получать хорошие решения.
Последняя аналогия — классическая термодинамика, как область естествознания, полностью построена на эмпирике. Хочу привести цитату А. Эйнштейна* по этому поводу: «Теория производит тем большее впечатление, чем проще ее предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область её применения. Отсюда глубокое впечатление, которое произвела на меня классическая термодинамика. Это единственная физическая теория общего содержания, относительно которой я убежден, что в рамках применимости ее основных понятий она никогда не будет опровергнута (к особому сведению принципиальных скептиков)» — не замечаете ли аналогии?
* (Цит. по: Кириллин Б. Л., Сычев В. В., Шейндлин А. Е. Техническая термодинамика, 3-е изд. М., 1979, с. 502.)
Соглашусь, что мой стиль предвзят. Это продиктовано тем, что
— конкретно в случае задачи регрессии есть более эффективные решения, и я уже встречался с крайне необдуманными применениями ГП как технологии (я не имею ввиду вас). Что, разумеется, говорит не столько о технологии, сколько о применяющих. С другой стороны, у каждой технологии, кроме собственно технологии, есть свой «маркетинг», и не всегда он приносит пользу тем, кто готов бездумно таковую технологию применить. Под маркетингом я имею ввиду вещи вроде «ТеХом пользоваться очень просто!», «ГП это универсальная технология». Это разумные утверждения, которые как правило не идут против истины, но в конечно счете могут приводить к не самому адекватному расположению рекламируего «товара» в системе представлений.
Может показаться, что я вцепился в ваш пример именно символьной регрессии и упускаю все прочие более удачные применения ГП как технологии. Да, наверное так. Но именно потому, что этот конкретный пример правда считаю крайне неудачным, по описанным выше причинам. Что, еще раз, не говорит, что мне не симпатичен ваш опыт в крайне разнообразных задачах. Мне было интересно посмотреть ваши демки и я вполне согласен, что в ситуации, когда модели нет, ГП поставляет неплохой инструмент для ее поиска.
— чтобы более осознанно выбирать технологию, следует знать об альтернативах и — тут ключевое — иметь возможность сравнивать эффективность этих технологий и отдельных их составляющих. Хотя бы как-нибудь, поэтому академически точными понятиями увы, не всегда можно оперировать. А раз так, я осознанно выбрал стиль беседы «научная курилка», где легко переходят от интуитивных ощущений к формальным определениям и обратно, но все понимают, что задача не теорему доказать, а понимания достичь.
— вы мне исходно показались ГП-евангелистом без кругозора. Тут я признаю свою ошибку. Поэтому я и не отвечал на ваши каменты. Все ваши ответа на мои вопросы о сравнительной эффективности отдельных составляющих ГП даны с точки зрения универсальности ГП и правильности ее применения так, словно альтернатив нет. К тому же, некоторые ваши ответы, на мой взгляд, не несут цели разобраться в содержании, а только добавить формализма. Например, на вопрос о гладкости пространства поиска в свете применения различных оптимизаций, которые фактически являются достаточно значимыми интервенциями в исходную модель, вы лишь отвечаете классификацией собственных оптимизаций. При всем уважении к проделанной вами работе, отвечает ли такая классификация задаче разобраться о гладкости пространства поиска? На мой взгляд нет, но добавляет формализма и наукообразия, и будь я неуверенный студент, меня бы ваш ответ отпугнул вообще любые вопросы задавать. Заметьте, это добавляет наукообразия там, где я как раз стараюсь его избежать. Таким образом, нового понимания ГП у меня в разговоре не возникло. А жаль, могло возникнуть, если б беседа обернулась ссылкой на исследования, где терминология ГП транслируется в модели, напрямую допускающие оценку качества сходимости.
Теперь, спасибо что поймали на терминологических неточностях. Разумеется, физический смысл у точек пространства никуда не исчезает. Имел ввиду следующее: когда нужно посчитать некоторую статсумму, значимый вклад может дать суммирование по достаточно малому подмножеству индексов, и вот каких — заранее может быть неясно. И уже из необходимости как-то выбрать подмножество суммирования вводят распределение вероятностей. Так точнее?
Ваше замечание о моих задачах странное, потому что я никаких своих задач не упоминал.
— конкретно в случае задачи регрессии есть более эффективные решения, и я уже встречался с крайне необдуманными применениями ГП как технологии (я не имею ввиду вас). Что, разумеется, говорит не столько о технологии, сколько о применяющих. С другой стороны, у каждой технологии, кроме собственно технологии, есть свой «маркетинг», и не всегда он приносит пользу тем, кто готов бездумно таковую технологию применить. Под маркетингом я имею ввиду вещи вроде «ТеХом пользоваться очень просто!», «ГП это универсальная технология». Это разумные утверждения, которые как правило не идут против истины, но в конечно счете могут приводить к не самому адекватному расположению рекламируего «товара» в системе представлений.
Может показаться, что я вцепился в ваш пример именно символьной регрессии и упускаю все прочие более удачные применения ГП как технологии. Да, наверное так. Но именно потому, что этот конкретный пример правда считаю крайне неудачным, по описанным выше причинам. Что, еще раз, не говорит, что мне не симпатичен ваш опыт в крайне разнообразных задачах. Мне было интересно посмотреть ваши демки и я вполне согласен, что в ситуации, когда модели нет, ГП поставляет неплохой инструмент для ее поиска.
— чтобы более осознанно выбирать технологию, следует знать об альтернативах и — тут ключевое — иметь возможность сравнивать эффективность этих технологий и отдельных их составляющих. Хотя бы как-нибудь, поэтому академически точными понятиями увы, не всегда можно оперировать. А раз так, я осознанно выбрал стиль беседы «научная курилка», где легко переходят от интуитивных ощущений к формальным определениям и обратно, но все понимают, что задача не теорему доказать, а понимания достичь.
— вы мне исходно показались ГП-евангелистом без кругозора. Тут я признаю свою ошибку. Поэтому я и не отвечал на ваши каменты. Все ваши ответа на мои вопросы о сравнительной эффективности отдельных составляющих ГП даны с точки зрения универсальности ГП и правильности ее применения так, словно альтернатив нет. К тому же, некоторые ваши ответы, на мой взгляд, не несут цели разобраться в содержании, а только добавить формализма. Например, на вопрос о гладкости пространства поиска в свете применения различных оптимизаций, которые фактически являются достаточно значимыми интервенциями в исходную модель, вы лишь отвечаете классификацией собственных оптимизаций. При всем уважении к проделанной вами работе, отвечает ли такая классификация задаче разобраться о гладкости пространства поиска? На мой взгляд нет, но добавляет формализма и наукообразия, и будь я неуверенный студент, меня бы ваш ответ отпугнул вообще любые вопросы задавать. Заметьте, это добавляет наукообразия там, где я как раз стараюсь его избежать. Таким образом, нового понимания ГП у меня в разговоре не возникло. А жаль, могло возникнуть, если б беседа обернулась ссылкой на исследования, где терминология ГП транслируется в модели, напрямую допускающие оценку качества сходимости.
Теперь, спасибо что поймали на терминологических неточностях. Разумеется, физический смысл у точек пространства никуда не исчезает. Имел ввиду следующее: когда нужно посчитать некоторую статсумму, значимый вклад может дать суммирование по достаточно малому подмножеству индексов, и вот каких — заранее может быть неясно. И уже из необходимости как-то выбрать подмножество суммирования вводят распределение вероятностей. Так точнее?
Ваше замечание о моих задачах странное, потому что я никаких своих задач не упоминал.
Текущая ветка обсуждений получилась довольно интересной :-) Спасибо вам за замечания.
Однако, изначально, при написании данной статьи у меня была несколько иная цель — проиллюстрировать на простом примере концепцию ГП, предоставить людям работающий прототип, и поделиться собственными наблюдениями.
Здесь есть небольшая сводка математических моделей, в рамках которых были проанализированы некоторые аспекты ГП.
Относительно пространства поиска, в общем случае, можно заметить что оно бесконечномерное, а также, боюсь, что вопрос о его топологии связан с проблемой разрешимости — со всеми вытекающими отсюда последствиями.
Однако, изначально, при написании данной статьи у меня была несколько иная цель — проиллюстрировать на простом примере концепцию ГП, предоставить людям работающий прототип, и поделиться собственными наблюдениями.
Здесь есть небольшая сводка математических моделей, в рамках которых были проанализированы некоторые аспекты ГП.
Относительно пространства поиска, в общем случае, можно заметить что оно бесконечномерное, а также, боюсь, что вопрос о его топологии связан с проблемой разрешимости — со всеми вытекающими отсюда последствиями.
С этого-то я и начинал топик: «вместо того, чтобы самостоятельно выбирать алгоритм, разработаем программу, которая способна автоматически генерировать алгоритмы для решения задач».
Конечно, любой частный алгоритм, разработанный для конкретной задачи или модели — будет лучше общего подхода.
Но я фокусировался именно на общем подходе, и рассмотрел символьную регрессию, как пример, в свете оного, дабы показать что таким образом тоже можно получать адекватные решения
Относительно сходимости — её нельзя рассматривать отдельно от типа эволюционный стратегии (проще говоря — параметров генетического алгоритма)
Конечно, любой частный алгоритм, разработанный для конкретной задачи или модели — будет лучше общего подхода.
Но я фокусировался именно на общем подходе, и рассмотрел символьную регрессию, как пример, в свете оного, дабы показать что таким образом тоже можно получать адекватные решения
Относительно сходимости — её нельзя рассматривать отдельно от типа эволюционный стратегии (проще говоря — параметров генетического алгоритма)
Вы все правильно говорите, когда разговор заходит о широком классе задач с неизвестной структурой предметной области. Тут и правда, остается только закодировать широкий набор эволюционных стратегий и молиться на теорему Пуанкаре о возвращении. Благо, оно работает лучше, чем просто случайное блуждание, и, в общем, неясно почему. (Рассуждения об эффективности эволюции меня не очень устраивают, пока нет доказательных исследований, какие конкретно эволюционные стратегии приводят к каким результатам — с цифрами в руках на больших выборках для специфических задач. А судя по каментам выше, общей теории нет и неясно, возможна ли она.)
Другое дело, когда речь идет о конкретной задаче регрессии, где структура предметной области известна и неплохо изучена. В этом частном случае применение ГП по меньшей мере заставляет задавать вопросы, ибо, казалось бы, можно взять аппроксиманд Паде, из априорной оценки точности определить требуемые степени полиномов числителя и знаменателя, а затем решить банальную систему линейных уравнений. Вычислительно это должно быть в разы, если не в десятки раз эффективнее. Другое дело, будет ли результат обладать интересующими вас свойствами, которые вы не закодировали набором точек. Но ведь, кажется, вы в данном топике даете пример только регрессии?
Другое дело, когда речь идет о конкретной задаче регрессии, где структура предметной области известна и неплохо изучена. В этом частном случае применение ГП по меньшей мере заставляет задавать вопросы, ибо, казалось бы, можно взять аппроксиманд Паде, из априорной оценки точности определить требуемые степени полиномов числителя и знаменателя, а затем решить банальную систему линейных уравнений. Вычислительно это должно быть в разы, если не в десятки раз эффективнее. Другое дело, будет ли результат обладать интересующими вас свойствами, которые вы не закодировали набором точек. Но ведь, кажется, вы в данном топике даете пример только регрессии?
Конечно, можно попытаться втиснуть задачу в рамки конкретного метода аппроксимации, но я акцентирую внимание на автоматическом конструировании модели.
При таком подходе, множество функций можно легко расширить до неаналитических, использовать шаблоны, работать с любым количеством переменных, использовать трансцендентные функции ( habrahabr.ru/post/163195/#comment_5611389 ), можно даже реализовать рекурсивные отношения.
Такой подход позволяет спокойно работать с данными, которые тяжело представить в виде функциональной зависимости. Всё тот же пример — демка 1
Я искал нейронную сеть, которая позволит максимизировать эффективность не отдельно взятого агента, а коллективную эффективность группы агентов в незнакомой среде.
Поэтому на каждом шаге генетического алгоритма, для каждой нейронной сети — я проверял насколько эффективно будет действовать группа агентов, каждый из которых управляется этой нейронной сетью (фактически подсчитывал суммарное количество «еды», собранной агентами).
Генетическое программирование эффективно использовать в задачах, которые трудно формализировать. Если же задачу формализировать достаточно просто, то можно использовать алгоритм специально разработанный для данной предметной области, но в то же время — приемлемые результаты можно получить и с помощью генетического программирования. Именно это я и продемонстрировал в топике.
При таком подходе, множество функций можно легко расширить до неаналитических, использовать шаблоны, работать с любым количеством переменных, использовать трансцендентные функции ( habrahabr.ru/post/163195/#comment_5611389 ), можно даже реализовать рекурсивные отношения.
Такой подход позволяет спокойно работать с данными, которые тяжело представить в виде функциональной зависимости. Всё тот же пример — демка 1
Я искал нейронную сеть, которая позволит максимизировать эффективность не отдельно взятого агента, а коллективную эффективность группы агентов в незнакомой среде.
Поэтому на каждом шаге генетического алгоритма, для каждой нейронной сети — я проверял насколько эффективно будет действовать группа агентов, каждый из которых управляется этой нейронной сетью (фактически подсчитывал суммарное количество «еды», собранной агентами).
Генетическое программирование эффективно использовать в задачах, которые трудно формализировать. Если же задачу формализировать достаточно просто, то можно использовать алгоритм специально разработанный для данной предметной области, но в то же время — приемлемые результаты можно получить и с помощью генетического программирования. Именно это я и продемонстрировал в топике.
Спасибо за интересный рассказ.
Кстати те задачи что вы решаете при помощи генетического программирования, можно гораздо быстрее и эффективнее решить при помощи Дискретного преобразование Фурье
Кстати те задачи что вы решаете при помощи генетического программирования, можно гораздо быстрее и эффективнее решить при помощи Дискретного преобразование Фурье
Опишите, пожалуйста, как с помощью ДПФ можно получить формулу f(x, y, z) = x^2 + 3*x + 2*y + z + 5 из описанного в топике эксперимента?
И совсем непонятно, каким образом ДПФ поможет, например, для автоматического конструирования нейронной сети?
Спасибо
И совсем непонятно, каким образом ДПФ поможет, например, для автоматического конструирования нейронной сети?
Спасибо
Ваш алгоритм тоже выдает не такой результат, если строго. Но вообще я имел ввиду задачу восстановления символьного представления функции по дискретным точкам. Если мне не изменяет память, любую функцию можно представить в виде бесконечного ряда Фурье. Соответственно и полученный ряд привести к исходному виду функции можно.
А про нейросеть да, наверное вы правы.
А про нейросеть да, наверное вы правы.
А из каких соображений накладывается ограничение на высоту дерева? Эвристически в зависимости от исходных данных? Или используется какая-то регуляризация?
Этому есть несколько причин:
- для того чтоб контролировать размер популяции в памяти
- размер дерева влияет на скорость вычисления соответствующей формулы
- эмпирически установил, что ограничения на 6-7 уровневую глубину дерева, и правильно подобранного множества базисных функций — должно быть достаточно для конструирования приемлемого решения
- также, я заметил что в данной задаче, небольшие мутации, в применении к огромным деревьям, не привносят качественно лучшие решения
Скажите а как обстоят дела с асимптотикой? Для примера у меня есть набор точек, который лежит в интервале от -1 до 1 по х, и от -1 до 1 по у. Я знаю, что при y->бесконечность, у меня есть асимптота ( грубо говоря график очень похож на тангенс), какова вероятность, что я ее получу?
Ваш вопрос можно рассмотреть в контексте вопроса про экстраполяцию: habrahabr.ru/post/163195/#comment_5610933, на который я дал ответ с примером.
В общем, правильный результат отыскивается довольно быстро если в наборе базовых функций содержатся функции, комбинация которых позволяет построить искомую зависимость, и если искомая формула имеет не очень сложную структуру (к сожалению, пока что, не могу привести конкретных цифр, а только собственные наблюдения).
Вот пример с асимптотической функцией:
Ищем функцию:
f(x) = 2/x
И уже на 10-й итерации получаем ответ:
f(x) = (((-40.187091057457245) / x) * (-0.04967024882881388))
В общем, правильный результат отыскивается довольно быстро если в наборе базовых функций содержатся функции, комбинация которых позволяет построить искомую зависимость, и если искомая формула имеет не очень сложную структуру (к сожалению, пока что, не могу привести конкретных цифр, а только собственные наблюдения).
Вот пример с асимптотической функцией:
Ищем функцию:
f(x) = 2/x
Исходные данные
# allowed functions are: ADD SUB MUL DIV SQRT POW LN SIN COS
# set which functions to use:
ADD MUL SUB DIV POW SQRT
# looking for:
f(x) - ?
# define training set:
f(-1) = -2
f(-0.9) = -2.222222222
f(-0.8) = -2.5
f(-0.7) = -2.857142857
f(-0.6) = -3.333333333
f(-0.5) = -4
f(-0.4) = -5
f(-0.3) = -6.666666667
f(-0.2) = -10
f(-0.1) = -20
f(0.1) = 20
f(0.2) = 10
f(0.3) = 6.666666667
f(0.4) = 5
f(0.5) = 4
f(0.6) = 3.333333333
f(0.7) = 2.857142857
f(0.8) = 2.5
f(0.9) = 2.222222222
f(1) = 2
threshold = 5
И уже на 10-й итерации получаем ответ:
f(x) = (((-40.187091057457245) / x) * (-0.04967024882881388))
лог эксперимента
Start time is: Fri Dec 21 16:30:21 EET 2012
f(x) = (x + x)
1 1110.6141849372693
f(x) = (x * 5.227087163426092)
2 1032.0300015165594
f(x) = (x * 5.188903230694518)
3 1032.0222453656522
f(x) = ((x + x) * 2.599190101196649)
4 1032.0220755614089
5 1032.0220755614089
f(x) = (((x + x) * (-0.12522500922214785)) * (-20.749626688467036))
6 1032.022006105762
7 1032.022006105762
f(x) = (x * 5.19507279952461)
8 1032.0219777015882
f(x) = (x * sqrt(abs(((-33.321388309286405) / x))))
9 873.1171859876806
f(x) = (((-40.187091057457245) / x) * (-0.04967024882881388))
10 0.004707596212974934
Best function is:
f(x) = (((-40.187091057457245) / x) * (-0.04967024882881388))
End time is: Fri Dec 21 16:30:25 EET 2012
У вас в исходных данных видны большие значения х, у — вопрос, если бы все координаты точек были в пределах -1,1 можно было бы получить асимпототу ( другой пример — имеем синус, вырезаем все что по х от -0.5 до 0.5 — есть ли вероятность на таких данных получить синус с присущим ему ограничением по у, или всегда будет полином?)
Конечно, если в базовом наборе есть функция sin — ничто не мешает, в результате мутации поместить в корень синтаксического дерева функцию sin.
Хотя, как вы понимаете, по очень маленькому и монотонному промежутку данных — невозможно однозначно определить функцию. Поэтому, на промежутке по х от -0.5 до 0.5, с одинаковой вероятностью можно получить как линейную, так и синусоидальную зависимость.
Относительно тригонометрических функций, я приводил экмпреримент в данном комментарии: habrahabr.ru/post/163195/#comment_5611389
Хотя, как вы понимаете, по очень маленькому и монотонному промежутку данных — невозможно однозначно определить функцию. Поэтому, на промежутке по х от -0.5 до 0.5, с одинаковой вероятностью можно получить как линейную, так и синусоидальную зависимость.
Относительно тригонометрических функций, я приводил экмпреримент в данном комментарии: habrahabr.ru/post/163195/#comment_5611389
кстати, для профессионального использования ГП часто используются специально разработанные для этого языки, например язык PUSH
faculty.hampshire.edu/lspector/push3-description.html
faculty.hampshire.edu/lspector/push.html
sourceforge.net/projects/push-evolve/
PUSH дает возможность вместо использования циклов (которые в ГП сильно тормозят весь процесс) — проход по спискам, ну и еще много других плюшек.
faculty.hampshire.edu/lspector/push3-description.html
faculty.hampshire.edu/lspector/push.html
sourceforge.net/projects/push-evolve/
PUSH дает возможность вместо использования циклов (которые в ГП сильно тормозят весь процесс) — проход по спискам, ну и еще много других плюшек.
Да, ещё очень удобным является тип данных CODE, который, по сути, предоставляет всю функциональность необходимую для ГП.
Также, как мне кажется, наиболее удобно и эффективно оперировать синтаксическими конструкциями, которые соответствуют чистым функциональным программам. Исходя из их лаконичности, а соответственно — небольшой сложности синтаксического дерева, это положительно сказывается на скорости нахождения решения, а также значительно помогает при последующем анализе и упрощении решения.
Например:
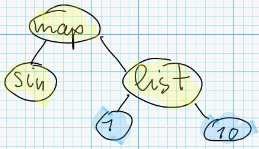
То же самое, в императивном стиле:

Также, как мне кажется, наиболее удобно и эффективно оперировать синтаксическими конструкциями, которые соответствуют чистым функциональным программам. Исходя из их лаконичности, а соответственно — небольшой сложности синтаксического дерева, это положительно сказывается на скорости нахождения решения, а также значительно помогает при последующем анализе и упрощении решения.
Например:
map(sin, list(1, 10))
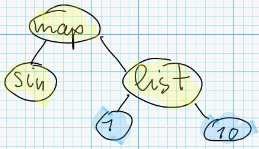
То же самое, в императивном стиле:
for(int i = 1; i < 11; i++) {
arr[i] = sin(i);
}
return arr;

Чисто функциональный стиль действительно удобнее.
И он ликвидирует циклы типа for(i=0;i<bigvalue;i++) { expensive useless code }
которые приводят к резкой деградации производительности.
В императивном стиле вместо них есть команда push которая наполняет список и циклы по спискам, таким образом длинных бесполезных циклов практически нет.
В функциональном все вообще проще.
Но был один вариант ГП, который использовал side-effects и иногда срабатывал неплохо — с индексными переменными.
Для каждого экземляра задавался небольшой массив, обнуляемый в начале вычислений.
А среди функций были операторы read[i] и write[i,tree value], которые читали и писали значения в этот массив.
Кстати первыми популярными имплементациями ГП были программы на Лиспе, что не могло не наложить отпечаток на технологию.
Лисп достаточно практичен для ГП.
И он ликвидирует циклы типа for(i=0;i<bigvalue;i++) { expensive useless code }
которые приводят к резкой деградации производительности.
В императивном стиле вместо них есть команда push которая наполняет список и циклы по спискам, таким образом длинных бесполезных циклов практически нет.
В функциональном все вообще проще.
Но был один вариант ГП, который использовал side-effects и иногда срабатывал неплохо — с индексными переменными.
Для каждого экземляра задавался небольшой массив, обнуляемый в начале вычислений.
А среди функций были операторы read[i] и write[i,tree value], которые читали и писали значения в этот массив.
Кстати первыми популярными имплементациями ГП были программы на Лиспе, что не могло не наложить отпечаток на технологию.
Лисп достаточно практичен для ГП.
Поясните мне, плиз, как замена цикла по массиву на итератор по сконструированному на основе массива списку увеличивает производительность обработки всех элементов массива?
Сам массив меньше получается — он же рандомный.
При обычном цикле генерируются фрагменты типа
Соответственно y может быть сколь угодно большим, при том, что полезной нагрузки внутри цикла может и не быть — там же рандомный код, а то и вообще интрон, результат вычисления которого потом теряется.
А вот если код вместо явных конструкций цикла имеет вид
То объем получающегося списка обычно небольшой и соответственно время нахождения в цикле тоже разумное.
Поэтому конструкции типа for/while редко используют в ГП, предпочитая работу со списками в функциональном стиле или близкую к ним.
В классическом ГП циклов кстати вообще не было, потом рекурсию ввели, но там тоже проблем хватало.
При обычном цикле генерируются фрагменты типа
const int x=rand();
const int y=rand();
for(i=x;i<y;i++)
{
random code
}
Соответственно y может быть сколь угодно большим, при том, что полезной нагрузки внутри цикла может и не быть — там же рандомный код, а то и вообще интрон, результат вычисления которого потом теряется.
А вот если код вместо явных конструкций цикла имеет вид
push(list,value1);
...
push(list,value2);
...
foreach(list) // or while(val=pop(list))
{
do something
}
То объем получающегося списка обычно небольшой и соответственно время нахождения в цикле тоже разумное.
Поэтому конструкции типа for/while редко используют в ГП, предпочитая работу со списками в функциональном стиле или близкую к ним.
В классическом ГП циклов кстати вообще не было, потом рекурсию ввели, но там тоже проблем хватало.
А не хотите ли Вы попробовать поработать не с формулами а с алгоритмами, то есть с такими деревьями, у которых еще могут быть и логические ветвления или вообще циклы. Я разработал специальный язык для таких экспериментов "Автор".
Sign up to leave a comment.
Символьная регрессия