Добрый день, уважаемые коллеги. В этой статье я хочу поделиться с Вами своими методическими наработками, которые использую в курсе «Теория автоматического управления» на кафедре СУиИ НИУ ИТМО.
Основной задачей, которую я перед собой ставил, было объединение теоретических знаний для решения практической задачи. Такой задачей стало управление приводами Lego робота. Лишний повод поиграть в игрушки, да и студентам проще воспринимать суровый матан… Вот пример описания этого набора: habrahabr.ru/post/166449.
Пойдем по порядку, для начала нужно было составить адекватную математическую модель двигателя. И уже здесь я столкнулся с проблемой: производители не указали технических характеристик двигателей в наборе. Поиcк в Google дает некоторое количество вариантов (например, nxt-unroller.blogspot.ru/2011/01/motor-controller-with-feed-forward-for.html или philohome.com/nxtmotor/nxtmotor.htm), но мне нужно было получить характеристики тех двигателей, которые использовались в роботе. Вот тут и пригодилось знание физики и теоретической механики.
Составим уравнение Лагранжа-Эйлера и учтем влияние противо-ЭДС в обмотке ротора двигателя постоянного тока (ДПТ), получим:
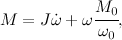
где w — угловая скорость вращения мотора,w0 — скорость холостого хода, M — момент развиваемый двигателем, M0 — пусковой момент, J — момент инерции ротора двигателя. Решением дифференциального уравнения будет следующее выражение:
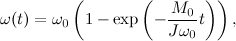
где J*w0/M0 = Tm, Tm — это электромеханическая постоянная двигателя.
Функция изменения угла во времени будет интегралом функции скорости с учетом начальных условий:

Как раз-таки она нам и нужна.
Далее, нужно было написать программу, которая снимет характеристику разгона ДПТ, описанную обозначенным уравнением. Для этого использовал nxcEditor для Linux и Bricxcc для Windows. На выходе получил файл, содержащий значения угла и соответствующие им показания времени.
Данные с двигателя обработал в Scilab (открытый аналог Matlab), получив значения электромеханической постоянной и установившейся скорости вращения двигателя методом наименьших квадратов, которые будут равны aa(2)=Tm=0.081[сек] и aa(1)=w0=14.7[рад/сек] соответственно.

И проверить справедливость полученных значений, подав на двигатель управление в виде синусоиды (на изображении приведены графики реакции математической модели и реального двигателя, график реального двигателя уплывает вниз из-за разнсти сопротивлений в цепи двигателя, при вращении по часовой стрелке и против, на котрое влияет силовой ключ):

Теперь можно было спокойно перейти к вычислению коструктивных постоянных двигателя, которые необходимы для управления его моментом. Для этого воспользовался системой уравнений двигателя, описывающих электрические процессы:
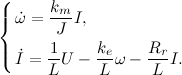
где ke,km — конструктивные постоянные, U=7[В] — управляющее напряжение, L=0.0047[Гн] — индуктивность обмотки, Rr=6[Ом] — сопротивление обмотки робота,. Измерил пусковой ток I=0.9[А] (измеряется при стопорении ротора) и рассчитал момент инерции ротора. Пользуясь следующей формулой, получил пусковой момент, выдаваемый двигателем:
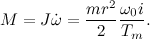
В уравнении i= 48 — коэффициент редукции. Коэффициент передачи по току получил равным 0.42, поделив пусковой момент на выходном валу на пусковой ток
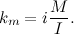
Коэффициент передачи противоЭДС, равный 0.48, вычислил, как отношение установившейся угловой скорости к подаваемому напряжению
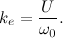
Следующий шаг, запрограммировать управление углом поворота ДПТ. Для этого использовал пропорциональный регулятор. Программная реализация выглядит следующим образом:
И вот наступает момент истины, насколько наша расчитанная модель соответствует реальной ситуации (модель собиралась в Scilab Xcos).

Привожу модельную и экспериментальную кривую:
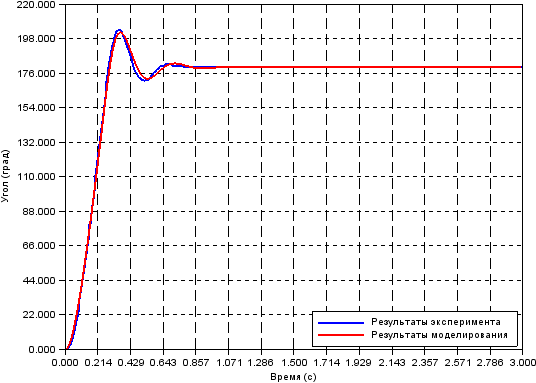
Как видите, все сходится с отклонением не более 3 %.
Такие простые эксперименты, проделанные собственными руками, позволяют понять основы математического моделирования и теории управления.
В свою очередь готов поделиться пособием для выполнения работ.
С удовольствием выслушаю Ваши отзовы и предложения.
Основной задачей, которую я перед собой ставил, было объединение теоретических знаний для решения практической задачи. Такой задачей стало управление приводами Lego робота. Лишний повод поиграть в игрушки, да и студентам проще воспринимать суровый матан… Вот пример описания этого набора: habrahabr.ru/post/166449.
Пойдем по порядку, для начала нужно было составить адекватную математическую модель двигателя. И уже здесь я столкнулся с проблемой: производители не указали технических характеристик двигателей в наборе. Поиcк в Google дает некоторое количество вариантов (например, nxt-unroller.blogspot.ru/2011/01/motor-controller-with-feed-forward-for.html или philohome.com/nxtmotor/nxtmotor.htm), но мне нужно было получить характеристики тех двигателей, которые использовались в роботе. Вот тут и пригодилось знание физики и теоретической механики.
Составим уравнение Лагранжа-Эйлера и учтем влияние противо-ЭДС в обмотке ротора двигателя постоянного тока (ДПТ), получим:
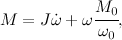
где w — угловая скорость вращения мотора,w0 — скорость холостого хода, M — момент развиваемый двигателем, M0 — пусковой момент, J — момент инерции ротора двигателя. Решением дифференциального уравнения будет следующее выражение:
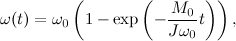
где J*w0/M0 = Tm, Tm — это электромеханическая постоянная двигателя.
Функция изменения угла во времени будет интегралом функции скорости с учетом начальных условий:

Как раз-таки она нам и нужна.
Далее, нужно было написать программу, которая снимет характеристику разгона ДПТ, описанную обозначенным уравнением. Для этого использовал nxcEditor для Linux и Bricxcc для Windows. На выходе получил файл, содержащий значения угла и соответствующие им показания времени.
Данные с двигателя обработал в Scilab (открытый аналог Matlab), получив значения электромеханической постоянной и установившейся скорости вращения двигателя методом наименьших квадратов, которые будут равны aa(2)=Tm=0.081[сек] и aa(1)=w0=14.7[рад/сек] соответственно.
data=read("/home/kasper/Number.txt",-1,2);
time=(data(:,2)-data(1,2))/1000;
angle=data(:,1)*%pi/180;
angle=angle';
time=time';
f=[time;angle];
function e=G(a, z),
e = z(2) - a(1)*(z(1)-a(2)+a(2)*%e^(-z(1)/a(2)));
endfunction
a0=[1;4];
[aa,er]=datafit(G,f,a0);
model=aa(1)*(time+aa(2)*(%e^(-time/aa(2))-1));
xtitle('Зависимость угловой скорости от времени','time','$\dot\phi,[\frac{рад}{сек}]$');
plot2d(time,model,[5]);
a=gca();
a.children.children(1).thickness=2;
plot2d(time,angle,[2]);
a.children.children(1).thickness=2;
a.children.children(1).text=["$\dot\phi(t)$"];

И проверить справедливость полученных значений, подав на двигатель управление в виде синусоиды (на изображении приведены графики реакции математической модели и реального двигателя, график реального двигателя уплывает вниз из-за разнсти сопротивлений в цепи двигателя, при вращении по часовой стрелке и против, на котрое влияет силовой ключ):

Теперь можно было спокойно перейти к вычислению коструктивных постоянных двигателя, которые необходимы для управления его моментом. Для этого воспользовался системой уравнений двигателя, описывающих электрические процессы:
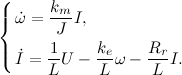
где ke,km — конструктивные постоянные, U=7[В] — управляющее напряжение, L=0.0047[Гн] — индуктивность обмотки, Rr=6[Ом] — сопротивление обмотки робота,. Измерил пусковой ток I=0.9[А] (измеряется при стопорении ротора) и рассчитал момент инерции ротора. Пользуясь следующей формулой, получил пусковой момент, выдаваемый двигателем:
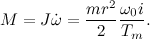
В уравнении i= 48 — коэффициент редукции. Коэффициент передачи по току получил равным 0.42, поделив пусковой момент на выходном валу на пусковой ток
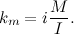
Коэффициент передачи противоЭДС, равный 0.48, вычислил, как отношение установившейся угловой скорости к подаваемому напряжению
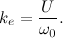
Следующий шаг, запрограммировать управление углом поворота ДПТ. Для этого использовал пропорциональный регулятор. Программная реализация выглядит следующим образом:
#define NEED_ANGLE 180
#define WORK_TIME 3000
#define KOL_EXPS 3
#define PORT OUT_A
#define KP 14
task main()
{
int angle_now, battery_voltage, power_percent, time = 0;
int i, str_size, file_size = 8224;
byte file;
string str = "3lab.txt";
float need_voltage, angle_diff;
DeleteFile(str);
CreateFile(str, file_size, file);
while(time < WORK_TIME)
{
angle_now = MotorRotationCount(PORT);
time = CurrentTick() - FirstTick();
angle_diff = NEED_ANGLE - angle_now;
angle_diff = angle_diff * 3.1415 / 180;
need_voltage = KP * angle_diff;
need_voltage *= 1000;
battery_voltage = BatteryLevel();
power_percent = need_voltage / battery_voltage * 100;
if(abs(power_percent) > 100) power_percent = 100 * sign(power_percent);
OnFwd(PORT, power_percent);
str = NumToStr(angle_now) + " " + NumToStr(time);
WriteLnString(file, str, str_size);
Wait(MS_5);
}
Off(PORT);
CloseFile(file);
}
И вот наступает момент истины, насколько наша расчитанная модель соответствует реальной ситуации (модель собиралась в Scilab Xcos).

Привожу модельную и экспериментальную кривую:

Как видите, все сходится с отклонением не более 3 %.
Такие простые эксперименты, проделанные собственными руками, позволяют понять основы математического моделирования и теории управления.
В свою очередь готов поделиться пособием для выполнения работ.
С удовольствием выслушаю Ваши отзовы и предложения.