Давным-давно, когда трава была зеленее, а деревья выше, жил-был тролль, по имени Xenocephal. Жил он, в принципе, во многих местах, но мне повезло встретить его на одном форуме, где я, в то время, набирался ума-разума. Я уже не вспомню топика, в котором протекала беседа, но суть ее сводилась к тому, что Xenocephal пытался убедить всех окружающих, что Lisp (с его макросами) — всему голова, а C++, с его шаблонами, жалкое подобие левой руки. Также утверждалось, что наметапрограммировать в нем что-то сложнее набившего оскомину факториала не представляется возможным.
У меня, в принципе, не было возражений, что макросы Lisp-а — это непомерно круто и, в то время, мне нечего было ему ответить, но фраза про шаблоны C++ и факториал глубоко засела в мой неокрепший мозг и продолжала терзать меня изнутри. И в один ужасный день, я подумал: «Какого черта??? Давайте пометапрограммируем!»
Другим источником вдохновения послужила Книга Дракона. Задача нашлась быстро. Я счел, что алгоритм преобразования Недетерминированного Конечного Автомата (НКА) в Детерминированный Конечный Автомат (ДКА) достаточно нетривиальна, чтобы попытаться реализовать ее при помощи шаблонов C++. Нетленный труд Александреску позволил набрать критическую массу…
Начал я, разумеется, с примитивов. Мне требовалось, каким-то образом представлять графы:
Дуга графа задавалась индексами начальной (Src) и конечной (Dst) вершин и могла быть поименована символом (Chr). Не именованные дуги (используемые алгоритмом преобразования), по умолчанию, помечались нулевым символом. Тип Next, определенный в этом шаблоне, превращал его в список типов. Добавление дуги в этот список было реализовано следующим рекурсивным образом:
Аналогично, было организовано слияние списков (благодаря утиной типизации, любых, а не только тех, которые представляют графы):
… и применение произвольного функтора к каждому элементу списка:
Теперь, требовалось реализовать построение НКА на основе регулярного выражения. Сама методика этого построения хорошо описана в книге, упомянутой выше и сводится к тому, что элементы регулярного выражения заменяются некими базовыми конструкциями, связанными не именованными дугами.
Именованная дуга создается элементарно:
Начальная и конечная вершины получают индексы 0 и 1 соответственно.
Два графа могут быть связаны в конструкцию альтернативы /A|B/ следующим образом:
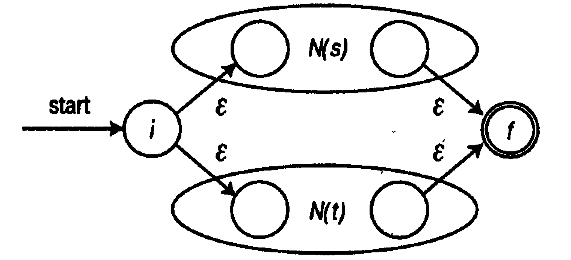
Здесь, мы «сливаем» два входных графа (A и B) (при этом их вершины перенумеруются), после чего, соединяем их не именованными дугами, по схеме, приведенной выше. Начальная и конечная вершины по прежнему имеют индексы 0 и 1 соответственно.
Несколько более сложной для понимания оказалась реализация следования /AB/:
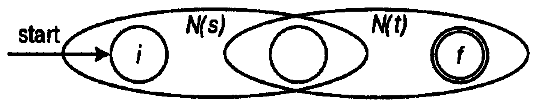
Здесь, дополнительные дуги не строятся, а графы соединяются общей вершиной (начальной для B и конечной для A).
Самой сложной оказалась реализация квантификатора /T*/:

Поскольку квантификаторы /T*/ и /T+/ встречаются довольно часто, были перегружены их оптимизированные реализации:
Теперь, можно было собрать НКА, представляющий регулярное выражение /(a|b)*abb/, описанное в книге:
Осталось преобразовать его в ДКА:
Я не буду подробно описывать все мытарства связанные с отладкой этого кода (чего стоили одни только километровые листинги с сообщениями об ошибках компиляции), замечу только, что «лобовая» реализация алгоритма вешала компилятор напрочь, в результате чего пришлось реализовать оптимизированный шаблон ImportantOpt.
Теперь можно запустить на выполнение следующий код:
… и убедиться, что выдаваемый им результат:
Соответствует искомому графу ДКА:
Как обычно, исходники выложены на GitHub.
У меня, в принципе, не было возражений, что макросы Lisp-а — это непомерно круто и, в то время, мне нечего было ему ответить, но фраза про шаблоны C++ и факториал глубоко засела в мой неокрепший мозг и продолжала терзать меня изнутри. И в один ужасный день, я подумал: «Какого черта??? Давайте пометапрограммируем!»
Другим источником вдохновения послужила Книга Дракона. Задача нашлась быстро. Я счел, что алгоритм преобразования Недетерминированного Конечного Автомата (НКА) в Детерминированный Конечный Автомат (ДКА) достаточно нетривиальна, чтобы попытаться реализовать ее при помощи шаблонов C++. Нетленный труд Александреску позволил набрать критическую массу…
Начал я, разумеется, с примитивов. Мне требовалось, каким-то образом представлять графы:
template <class T, int Src, int Dst, char Chr = 0>
struct Edge
{ enum { Source = Src,
Dest = Dst,
Char = Chr
};
typedef T Next;
static void Dump(void) {printf("%3d -%c-> %3d\n",Src,Chr,Dst);T::Dump();}
};
Дуга графа задавалась индексами начальной (Src) и конечной (Dst) вершин и могла быть поименована символом (Chr). Не именованные дуги (используемые алгоритмом преобразования), по умолчанию, помечались нулевым символом. Тип Next, определенный в этом шаблоне, превращал его в список типов. Добавление дуги в этот список было реализовано следующим рекурсивным образом:
struct NullType {static void Dump(void) {printf("\n");}};
template <int S, int D, int C, class T, class R> struct AddEdge;
template <int S, int D, int C, class R> struct AddEdge<S,D,C,NullType,R> {
typedef typename Edge<R,S,D,C> Result;
};
template <int S, int D, int C, class T, class R> struct AddEdge<S,D,C,Edge<T,S,D,C>,R> {
typedef typename AddEdge<S,D,C,T,R>::Result Result;
};
template <int S, int D, int C, int s, int d, int c, class T, class R>
struct AddEdge<S,D,C,Edge<T,s,d,c>,R> {
typedef typename AddEdge<S,D,C,T,Edge<R,s,d,c> >::Result Result;
};
Аналогично, было организовано слияние списков (благодаря утиной типизации, любых, а не только тех, которые представляют графы):
Append
template <class A, class B> struct Append;
template <class T> struct Append<NullType,T> {
typedef T Result;
};
template <int S, int D, int C, class T, class B>
struct Append<Edge<T,S,D,C>,B> {
typedef typename Append<T,Edge<B,S,D,C> >::Result Result;
};
Join
template <class A, class B> struct Join;
template <class B> struct Join<NullType,B> {
typedef B Result;
};
template <int N, class T, class B> struct Join<Set<N,T>,B> {
typedef typename Join<T,typename AddSet<N,B,NullType>::Result>::Result Result;
};
template <int S, int D, int C, class T, class B> struct Join<Edge<T,S,D,C>,B> {
typedef typename Join<T,typename AddEdge<S,D,C,B,NullType>::Result>::Result Result;
};
template <int N, class S, class T, class B> struct Join<StateList<N,S,T>,B> {
typedef typename Join<T,typename AddState<N,S,B,NullType>::Result>::Result Result;
};
template <int Src, int Dst, int a, class S, class T, class B>
struct Join<StateListEx<Src,Dst,a,S,T>,B> {
typedef typename Join<T,typename AddState<Dst,S,B,NullType>::Result>::Result Result;
};
… и применение произвольного функтора к каждому элементу списка:
Map
template <class T, int V, class R, template <int,int> class F> struct Map;
template <int V, class R, template <int,int> class F> struct Map<NullType,V,R,F> {
typedef R Result;
};
template <int N, class T, int V, class R, template <int,int> class F>
struct Map<Set<N,T>,V,R,F> {
typedef typename Map<T,V,Set<F<N,V>::Result,R>,F>::Result Result;
};
template <class T, int S, int D, int C, int V, class R, template <int,int> class F>
struct Map<Edge<T,S,D,C>,V,R,F> {
typedef typename Map<T,V,Edge<R,F<S,V>::Result,F<D,V>::Result,C>,F>::Result Result;
};
Теперь, требовалось реализовать построение НКА на основе регулярного выражения. Сама методика этого построения хорошо описана в книге, упомянутой выше и сводится к тому, что элементы регулярного выражения заменяются некими базовыми конструкциями, связанными не именованными дугами.
Именованная дуга создается элементарно:
C
template <char Chr>
struct C
{ typedef typename Edge<NullType,0,1,Chr> Result;
enum {Count = 2};
};
Начальная и конечная вершины получают индексы 0 и 1 соответственно.
Два графа могут быть связаны в конструкцию альтернативы /A|B/ следующим образом:

D
template <int X, int N>
struct Add { enum { Result = X+N }; };
template <class A, class B>
struct DImpl
{ private:
typedef typename Append<
typename Map<typename A::Result, 2, NullType, Add>::Result,
typename Map<typename B::Result, A::Count+2, NullType, Add>::Result
>::Result N0;
typedef typename Edge<N0,0,2> N1;
typedef typename Edge<N1,0,A::Count+2> N2;
typedef typename Edge<N2,3,1> N3;
public:
typedef typename Edge<N3,A::Count+3,1> Result;
enum {Count = A::Count+B::Count+2};
};
template <class T1, class T2, class T3 = NullType, class T4 = NullType, class T5 = NullType>
struct D: public DImpl<T1, D<T2,T3,T4,T5> > {};
template <class T1, class T2>
struct D<T1,T2,NullType,NullType,NullType>: public DImpl<T1,T2> {};
Здесь, мы «сливаем» два входных графа (A и B) (при этом их вершины перенумеруются), после чего, соединяем их не именованными дугами, по схеме, приведенной выше. Начальная и конечная вершины по прежнему имеют индексы 0 и 1 соответственно.
Несколько более сложной для понимания оказалась реализация следования /AB/:

E
template <int X, int N>
struct ConvA { enum { Result = (X==1) ? (X+N-1) : X }; };
template <int X, int N>
struct ConvB { enum { Result = (X==1) ? 1 : (X+N) }; };
template <class A, class B>
struct EImpl
{ private:
typedef typename Map<typename A::Result, A::Count, NullType, ConvA>::Result A1;
typedef typename Map<typename B::Result, A::Count, NullType, ConvB>::Result B1;
public:
typedef typename Append<A1,B1>::Result Result;
enum {Count = A::Count+B::Count};
};
template <class T1, class T2, class T3 = NullType, class T4 = NullType, class T5 = NullType>
struct E: public EImpl<T1, E<T2,T3,T4,T5> > {};
template <class T1, class T2>
struct E<T1,T2,NullType,NullType,NullType>: public EImpl<T1,T2> {};
Здесь, дополнительные дуги не строятся, а графы соединяются общей вершиной (начальной для B и конечной для A).
Самой сложной оказалась реализация квантификатора /T*/:

Q
template <class T, int Min = 0, int Max = 0> struct Q {
Q() {STATIC_ASSERT(Min<=Max, Q_Spec);}
private:
typedef typename Map<typename T::Result, T::Count, NullType, ConvA>::Result A1;
typedef typename Map<typename Q<T,Min,Max-1>::Result,T::Count,NullType,ConvB>::Result B1;
public:
typedef typename Edge<typename Append<A1,B1>::Result,0,T::Count> Result;
enum {Count = T::Count+Q<T,Min,Max-1>::Count};
};
template <class T, int N> struct Q<T,N,N>
{ private:
typedef typename Map<typename T::Result, T::Count, NullType, ConvA>::Result A1;
typedef typename Map<typename Q<T,N-1,N-1>::Result, T::Count, NullType, ConvB>::Result B1;
public:
typedef typename Append<A1,B1>::Result Result;
enum {Count = T::Count+Q<T,N-1,N-1>::Count};
};
Поскольку квантификаторы /T*/ и /T+/ встречаются довольно часто, были перегружены их оптимизированные реализации:
Q
template <class T> struct Q<T,1,1>: public T {};
template <class T>
struct Q<T,0,0>
{ private:
typedef typename Edge<typename Map<typename T::Result,2,NullType,Add>::Result,0,2> N0;
typedef typename Edge<N0,3,1> N1;
typedef typename Edge<N1,3,2> N2;
public:
typedef typename Edge<N2,0,1> Result;
enum {Count = T::Count+2};
};
template <class T>
struct Q<T,1,0>
{ public:
typedef typename Edge<typename T::Result,1,0> Result;
enum {Count = T::Count};
};
template <class T>
struct Q<T,0,1>
{ public:
typedef typename Edge<typename T::Result,0,1> Result;
enum {Count = T::Count};
};
Теперь, можно было собрать НКА, представляющий регулярное выражение /(a|b)*abb/, описанное в книге:
typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G;
Осталось преобразовать его в ДКА:
DFA
enum CONSTS {
MAX_FIN_STATE = 9
};
template <class Graph> class DFAImpl;
template <class T, int Src, int Dst, char Chr>
class DFAImpl<Edge<T,Src,Dst,Chr> >: public DFAImpl<typename T>
{ public:
typedef typename DFAImpl<typename T>::ResultType ResultType;
ResultType Parse(char C)
{
if ((State==Src)&&(C==Chr)) {
State = Dst;
if (State<MAX_FIN_STATE) {
State = 0;
return rtSucceed;
}
return rtNotCompleted;
}
return DFAImpl<typename T>::Parse(C);
}
void Dump(void) {T::Dump();}
};
template <>
class DFAImpl<NullType>
{ public:
DFAImpl(): State(0) {}
enum ResultType {
rtNotCompleted = 0,
rtSucceed = 1,
rtFailed = 2
};
ResultType Parse(char C)
{ State = 0;
return rtFailed;
}
protected:
int State;
};
// Вычисление хода (списка состояний) из вершины (При a==0 - e-ход)
// N - Узел
// T - Граф
// R - Результирующее состояние
// a - Символ алфавита
template <int N, class T, class R, int a = 0> struct Move;
template <int N, class R, int a> struct Move<N,NullType,R,a> {typedef R Result;};
template <int N, class T, int D, class R, int a> struct Move<N,Edge<T,N,D,a>,R,a>
{ typedef typename Move<N,T,typename AddSet<D,R,NullType>::Result,a>::Result Result;
};
template <int N, int M, class T, int D, class R, int a, int b>
struct Move<N,Edge<T,M,D,b>,R,a>
{ typedef typename Move<N,T,R,a>::Result Result;
};
// Фильтрация списка по условию F
// T - Исходный список (Set, StateListEx)
// С - Значение параметра предиката F
// R - Результирующий список (Set, StateListEx)
// F - Предикат (Exist, NotExist, Important)
template <class T, class C, class R, template <int,class> class F> struct Filter;
template <class C, class R, template <int,class> class F>
struct Filter<NullType,C,R,F> {typedef R Result;};
template <int N, class T, class C, class R, template <int,class> class F>
struct Filter<Set<N,T>,C,R,F>
{ typedef typename If<F<N,C>::Result,
typename Filter<T,C,typename Set<N,R>,F>::Result,
typename Filter<T,C,R,F>::Result
>::Result Result;
};
template <int Src, int Dst, int a, class S, class T, class C, class R, template <int,class> class F>
struct Filter<StateListEx<Src,Dst,a,S,T>,C,R,F>
{ typedef typename If<F<Dst,C>::Result,
typename Filter<T,C,typename StateListEx<Src,Dst,a,S,R>,F>::Result,
typename Filter<T,C,R,F>::Result
>::Result Result;
};
// Вычисление e-замыкания
// T - Начальный список узлов
// G - Граф
// R - Результирующий список узлов
template <class T, class G, class R> struct EClos;
template <class G, class R> struct EClos<NullType,G,R> {typedef R Result;};
template <int N, class T, class G, class R>
struct EClos<Set<N,T>,G,R>
{ private:
typedef typename Move<N,G,NullType>::Result L;
typedef typename Filter<L,typename Append<T,R>::Result,NullType,NotExist>::Result F;
public:
typedef typename EClos<typename Append<T,F>::Result,G,
typename Set<N,R>
>::Result Result;
};
// Вычисление хода из множества вершин
// T - Состояние
// G - Граф
// R - Результирующее состояние
// a - Символ алфавита
template <class T, class G, class R, int a> struct MoveSet;
template <class G, class R, int a> struct MoveSet<NullType,G,R,a> {typedef R Result;};
template <int N, class T, class G, class R, int a>
struct MoveSet<Set<N,T>,G,R,a>
{ typedef typename MoveSet<T,G,typename Join<R,typename Move<N,G,NullType,a>::Result>::Result,a>::Result Result;
};
// Вычисление списка состояний, полученных всеми ходами из вершины
// N - Генератор номеров узлов
// K - Генератор номеров финальных узлов
// T - Алфавит
// n - Текущий узел
// S - Текущее состояние (Set)
// G - Граф
// R - Результирующий список расширенных состояний
template <int N, int K, class T, int n, class S, class G, class R> struct MoveList;
template <int N, int K, int n, class S, class G, class R>
struct MoveList<N,K,NullType,n,S,G,R> {typedef R Result;};
template <int N, int K, int a, class T, int n, class S, class G, class R>
struct MoveList<N,K,Set<a,T>,n,S,G,R>
{ private:
typedef typename MoveSet<S,G,NullType,a>::Result S0;
typedef typename EClos<S0,G,NullType>::Result S1;
enum { N1 = (NotExist<1,S1>::Result)?K:N };
public:
typedef typename MoveList<(N==N1)?(N+1):N,
(K==N1)?(K+1):K,
T,n,S,G,
StateListEx<n,N1,a,S1,R> >::Result Result;
};
// Построение алфавита языка по графу NFA (вычислять однократно на верхнем уровне)
// T - Граф
// R - Результирующий алфавит
template <class T, class R> struct Alf;
template <class R> struct Alf<NullType,R> {typedef R Result;};
template <class T, int S, int D, class R> struct Alf<Edge<T,S,D,0>,R> {
typedef typename Alf<T,R>::Result Result;
};
template <class T, int S, int D, int a, class R> struct Alf<Edge<T,S,D,a>,R>{
typedef typename Alf<T, typename AddSet<a,R,NullType>::Result>::Result Result;
};
// Инкремент генератора узлов
// T - Список состояний (StateListEx)
// R - Результирующее значение генератора
// F - Предикат (Exist, NotExist)
template <class T, int R, template <int,class> class F> struct Incr;
template <int R, template <int,class> class F>
struct Incr<NullType,R,F> {enum {Result = R};};
template <int Src, int N, int a, class S, class T, int R, template <int,class> class F>
struct Incr<StateListEx<Src,N,a,S,T>,R,F>
{ enum { Result = Incr<T, (F<1,S>::Result)?((N>=R)?(N+1):R):R, F>::Result};
};
// Определение значимого узла
// N - Узел
// G - Граф
template <int N, class G> struct Important;
template <int N> struct Important<N,NullType> {enum {Result = (N==1)};};
template <int N, class T, int D>
struct Important<N,Edge<T,N,D,0> > {
enum { Result = Important<N,T>::Result };
};
template <int N, class T, int D, int C>
struct Important<N,Edge<T,N,D,C> > {
enum {Result = true};
};
template <int N, class T, int S, int D, int C>
struct Important<N,Edge<T,S,D,C> > {
enum { Result = Important<N,T>::Result };
};
// Оптимизированное построение списка значимых узлов
// T - Граф
// R - Результирующий список
template <class T, class R> struct ImportantOpt;
template <class R> struct ImportantOpt<NullType,R> {
typedef typename AddSet<1,R,NullType>::Result Result;
};
template <class T, int S, int D, class R>
struct ImportantOpt<Edge<T,S,D,0>,R>{
typedef typename ImportantOpt<T,R>::Result Result;
};
template <class T, int S, int D, int C, class R>
struct ImportantOpt<Edge<T,S,D,C>,R> {
typedef typename ImportantOpt<T,typename AddSet<S,R,NullType>::Result>::Result Result;
};
// Сравнение состояний по совокупности значимых узлов
// A - Список узлов (Set)
// B - Список узлов (Set)
// G - Граф
// I - Список значимых узлов (вычислять однократно на верхнем уровне)
template <class A, class B, class G> struct EquEx
{ private:
typedef typename Filter<A,G,NullType,Important>::Result A1;
typedef typename Filter<B,G,NullType,Important>::Result B1;
public:
enum { Result = Equ<A1,B1>::Result };
};
template <class A, class B, class I> struct EquExOpt
{ private:
typedef typename Filter<A,I,NullType,Exist>::Result A1;
typedef typename Filter<B,I,NullType,Exist>::Result B1;
public:
enum { Result = Equ<A1,B1>::Result };
};
// Получение списка узлов
// G - Граф
// R - Результирующий список
template <class T, class R> struct EdgeList;
template <class R>
struct EdgeList<NullType,R> {typedef R Result;};
template <class T, int S, int D, int C, class R>
struct EdgeList<Edge<T,S,D,C>,R>
{ private:
typedef typename AddSet<S,R, NullType>::Result R0;
typedef typename AddSet<D,R0,NullType>::Result R1;
public:
typedef typename EdgeList<T,R1>::Result Result;
};
// Проверка вхождения (по равенству состояний)
// T - Контрольный список (StateList)
// S - Искомое состояние (Set)
// I - Список значимых узлов
template <class T, class S, class I> struct ExistS;
template <class S, class I>
struct ExistS<NullType,S,I> {enum {Result = false};};
template <int N, class s, class T, class S, class I>
struct ExistS<StateList<N,s,T>,S,I>
{ enum { Result = (Equ<s,S>::Result) ? // EquExOpt<s,S,I>::Result
true :
ExistS<T,S,I>::Result
};
};
// Отброс ранее найденных узлов
// T - Исходный список (StateListEx)
// С - Контрольный список (StateList)
// I - Список значимых узлов (Set)
// R - Результирующий список (StateListEx)
template <class T, class C, class I, class R> struct FilterT;
template <class C, class I, class R>
struct FilterT<NullType,C,I,R> {typedef R Result;};
template <int Src, int Dst, int a, class S, class T, class C, class I, class R>
struct FilterT<StateListEx<Src,Dst,a,S,T>,C,I,R>
{ typedef typename If<ExistS<C,S,I>::Result,
typename FilterT<T,C,I,R>::Result,
typename FilterT<T,C,I,StateListEx<Src,Dst,a,S,R> >::Result
>::Result Result;
};
// Формирование результирующего графа
// T - Множество ранее сформированных вершин (StateList)
// a - Символ перехода к искомой вершине
// S - Исходное состояние (Set)
// I - Список значимых узлов
// R - Формируемый граф
template <class T, int Src, int Dst, int a, class S, class I, class R> struct GenImpl;
template <int Src, int Dst, int a, class S, class I, class R>
struct GenImpl<NullType,Src,Dst,a,S,I,R> {typedef R Result;};
template <int n, class s, class T, int Src, int Dst, int a, class S, class I, class R>
struct GenImpl<StateList<n,s,T>,Src,Dst,a,S,I,R>
{ typedef typename If<Equ<s,S>::Result, // EquExOpt<s,S,I>
Edge<R,Src,n,a>,
typename GenImpl<T,Src,Dst,a,S,I,R>::Result
>::Result Result;
};
// Формирование результирующего графа
// T - Множество новых узлов
// С - Ранее сформированные узлы
// I - Множество значимых узлов
// R - Результирующий граф
template <class T, class C, class I, class R> struct Gen;
template <class C, class I, class R>
struct Gen<NullType,C,I,R> {typedef R Result;};
template <int Src, int Dst, int a,class S, class T, class C, class I, class R>
struct Gen<StateListEx<Src,Dst,a,S,T>,C,I,R> {
typedef typename Gen<T,C,I,typename GenImpl<C,Src,Dst,a,S,I,R>::Result>::Result Result;
};
// Шаг преобразования
// N - Генератор номеров результирующих узлов
// K - Генератор номеров финальных узлов
// G - Граф (NFA)
// A - Алфавит (Set)
// I - Список значимых узлов (Set)
// R - Результирующий граф (DFA)
// M - Список помеченных состояний (StateList)
// D - Список непомеченных состояний (StateListEx)
template <int N, int K, class G, class A, class I, class R, class M, class D> struct ConvertImpl;
template <int N, int K, class G, class A, class I, class R, class M>
struct ConvertImpl<N,K,G,A,I,R,M,NullType> {typedef R Result;};
template <int N, int K, class G, class A, class I, class R, class M, int Src, int Dst, int a, class S, class D>
struct ConvertImpl<N,K,G,A,I,R,M,StateListEx<Src,Dst,a,S,D> >
{ private:
typedef typename MoveList<N,K,A,Dst,S,G,NullType>::Result T;
typedef typename StateList<Dst,S,M> M1;
typedef typename Append<D,M1>::Result MD;
typedef typename FilterT<T,MD,I,NullType>::Result T1;
typedef typename AppendSafe<T1,D>::Result D1;
typedef typename Gen<T,typename Append<T1,MD>::Result,I,R>::Result R1;
enum { N1 = Incr<T1,N,Exist>::Result,
K1 = Incr<T1,K,NotExist>::Result
};
public:
typedef typename ConvertImpl<N1,K1,G,A,I,R1,M1,D1>::Result Result;
};
// Преобразование NFA -> DFA
// G - Граф
// R - Результирующий граф
template <class G, class R> struct Convert
{ private:
typedef typename Alf<G,NullType>::Result A;
typedef typename ImportantOpt<G,NullType>::Result I;
public:
typedef typename ConvertImpl<1,MAX_FIN_STATE+1,G,A,I,NullType,NullType,
StateListEx<0,0,0,typename EClos<Set<0,NullType>,G,NullType>::Result,NullType> >::Result Result;
};
template <class T>
class DFA: public DFAImpl<typename Convert<typename T::Result,NullType>::Result> {};
Я не буду подробно описывать все мытарства связанные с отладкой этого кода (чего стоили одни только километровые листинги с сообщениями об ошибках компиляции), замечу только, что «лобовая» реализация алгоритма вешала компилятор напрочь, в результате чего пришлось реализовать оптимизированный шаблон ImportantOpt.
Теперь можно запустить на выполнение следующий код:
typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G;
typedef Convert<G,NullType>::Result R;
R::Dump();
… и убедиться, что выдаваемый им результат:
1 -a-> 10
1 -b-> 11
13 -a-> 10
13 -b-> 1
10 -a-> 10
10 -b-> 13
11 -a-> 10
11 -b-> 11
0 -a-> 10
0 -b-> 11
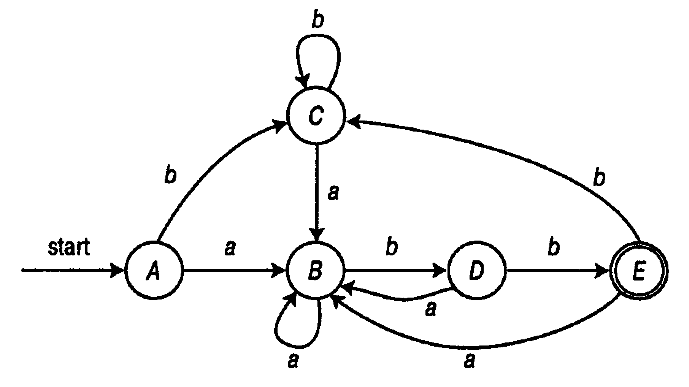
Соответствует искомому графу ДКА:

Как обычно, исходники выложены на GitHub.