скрин финального результата
В этой статье я рассказываю о том, как я изобрел свой личный велосипед, рисующий градиент практически как в фотошопе. Сразу предупреждаю, алгоритм ужасно медленный и неоптимизированный. Оптимизацией и рассмотрением какого-нибудь популярного алгоритма градиента я собираюсь заняться во второй части статьи
Зачем?
Как-то захотелось мне реализовать программную отрисовку градиентов, максимально похожих на фотошоповские. Никакой конкретной цели у меня не было, так, интересная задачка на вечер. В качестве языка была выбрана Java. Важной идеей было то, что я хотел написать этот алгоритм именно своими силами, не подглядывая в чужие алгоритмы.
Что должно было получиться
Метод drawGradient() должен работать следующим образом: мы задаем координаты и цвета двух точек, после чего поверх всего изображения рисуется градиент. Примерно так:
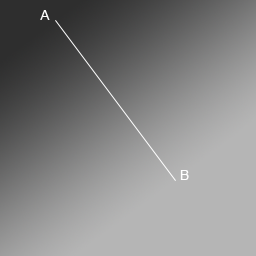
На данном рисунке точка A имеет координаты (55; 20) и цвет 0xff2e2e2e, а точка B — координаты (175; 180) и цвет 0xffb5b5b5. не забываем, что начало координат находится в левом верхнем углу, а ось Y направлена вниз.
Начинаем разбираться
В качестве эталона я взял градиент из фотошопа с прошлого скриншота. Как можно заметить, градиент состоит из трех частей:

Красная часть должна быть залита цветом точки А, зеленая — точки B, а цвет каждого пикселя оставшейся зоны должен вычисляться в зависимости от расстояния от него до прямых c и d.
Думаю очевидно, что нам нужен алгоритм, который будет определять расстояние от любого пикселя до прямых c и d. Также нужен способ для определения того, какой пиксель лежит в «красной» области, какой в «зеленой», а какой в оставшейся области.
Вспомним школьный курс геометрии и нарисуем следующую иллюстрацию для случайного пикселя E:
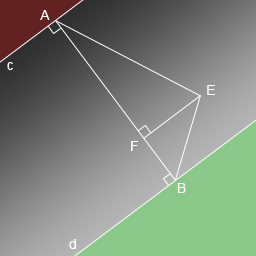
На данном рисунке AF — расстояние от пикселя E до прямой a. И, соответсвенно, FB — расстояние до прямой b. Именно эти расстояния и будут определять цвет пикселя. И тут же решается и проблема с определением того, к какой области относится пиксель. Тут все очень просто. Если AF + FB > AB, значит пиксель лежит либо в красной, либо в зеленой зоне. Чтобы определить в какой именно, сравним AF и FB. Если AF > FB, значит пиксель лежит в зеленой зоне, иначе в красной. Вот такая математика.
Итак, наша задача найти AF и BF. Сконцентрируемся на AF, по теореме Пифагора выходит, что:

Так, квадрат длины AE мы можем узнать из той же теоремы Пифагора, благо нам известны координаты точек A и E. Получается вот так:

Осталось найти только EF. Это немного потруднее, но ничего страшного. Так как наш отрезок EF представляет собой высоту треугольника, опущенную на сторону AB, нам поможет формула нахождения высоты. Выглядит она так:

А p — это одна из самых вводящих в заблуждение вещей. Это не периметр, а полупериметр. Помню пару раз совершал в школе фэйлы по этому поводу. Считается так:

AB и EB подсчитываем точно также как и AE — исходя из координат.
Итак, алгоритм подсчета AF как на ладони:
1. Рассчитываем AE, EB и AB
2. Рассчитываем p
3. Рассчитываем EF
4. Рассчитываем AF
Алгоритм для BF аналогичен, не буду его расписывать.
Самое время покодить!
Я решил создать класс, который представляет обертку для BufferedImage, назовем его EditableImage. И в этом классе, по моим прикидкам, должны были быть следующие методы:
EditableImage(int width, int height); //Конструктор
void clear(int color); //Сброс всех пикселей изображения в заданный цвет
void drawGradient(int x1, int y1, int color1, int x2, int y2, int color2); //Сам метод отрисовки градиентов
BufferedImage getImage(); //Метод для получения получившегося изображения
Тут и далее все цвета в моем коде задаются в виде int, который имеет следующий вид:
0xAARRGGBB
AA - значение прозрачности (у нас будут 32х битные картинки с прозрачностью)
RR - значение красного цвета
GG - значение зеленого цвета
BB - значение синего цвета
Идея с классом удобна тем, что если я потом захочу реализовать еще какие-нибудь фишки кроме градиента, это будет легко сделать.
Начнем со вспомогательных штук, которые к градиенту не имеют отношения
Gradient.java - точка входа программы
package ru.idgdima.gradient;
import javax.swing.*;
public class Gradient {
public static final int IMG_WIDTH = 640;
public static final int IMG_HEIGHT = 480;
private static GradientPanel panel; //Панель, которая будет рисовать наш градиент
public static void main(String[] args) {
//Создаем окно, заставляем его закрывать программу при нажатии на крест и
//запрещаем масштабирование окна
JFrame frame = new JFrame("Test");
frame.setDefaultCloseOperation(WindowConstants.EXIT_ON_CLOSE);
frame.setResizable(false);
//Создаем нашу панель для отрисовки градиента, добавляем ее в окно,
//подгоняем его размер под размер панели, размещаем окно по центру
//экрана и делаем его видимым
panel = new GradientPanel(IMG_WIDTH, IMG_HEIGHT);
frame.add(panel);
frame.pack();
frame.setLocationRelativeTo(null);
frame.setVisible(true);
}
}
GradientPanel.java - панель, на которой будет отображаться градиент
package ru.idgdima.gradient;
import javax.swing.*;
import java.awt.*;
import java.awt.image.BufferedImage;
public class GradientPanel extends JPanel {
private BufferedImage image;
public GradientPanel(int width, int height) {
//Вызываем конструктор родителя и устанавливаем размер панели
super();
setPreferredSize(new Dimension(width, height));
//Создаем изображение, заполняем его черными пикселями, рисуем
//на нем градиент и сохраняем его в качестве BufferedImage в поле
//класса для дальнейшей отрисовки
EditableImage gradientImage = new EditableImage(width, height);
gradientImage.clear(0xff000000);
gradientImage.drawGradient(55, 20, 0xff2e2e2e, 175, 180, 0xffb5b5b5);
image = gradientImage.getImage();
}
@Override
protected void paintComponent(Graphics g) {
super.paintComponent(g);
//В этом методе происходит отрисовка панели. Просто рисуем наше изображение
//поверх нее:
g.drawImage(image, 0, 0, null);
}
}
EditableImage.java - Самый интересный класс, метод для градиента пока пуст
package ru.idgdima.gradient;
import java.awt.image.BufferedImage;
public class EditableImage {
private int width;
private int height;
private int[] rgb; //все пиксели картинки будет храниться в этом массиве
BufferedImage image; //этот объект используется только для возвращения методом getImage
public EditableImage(int width, int height) {
this.width = width;
this.height = height;
rgb = new int[width * height]; //создаем массив достаточных размеров
//также создаем картинку для возвращения из метода getImage
image = new BufferedImage(width, height, BufferedImage.TYPE_4BYTE_ABGR);
}
/**
* Метод устанавливает всем пикселям изображения одинаковый цвет
* @param color желаемый цвет
*/
public void clear(int color) {
for (int i = 0; i < rgb.length; i++) {
rgb[i] = color;
}
}
/**
* Метод возвращает текущее изображение
* @return
*/
public BufferedImage getImage() {
//Копируем пиксели из массива rgb в image
image.setRGB(0, 0, width, height, rgb, 0, width);
return image;
}
public void drawGradient(int x1, int y1, int color1,
int x2, int y2, int color2) {
//пока пусто
}
}
Данную программу можно скомпилировать уже на этом этапе, но она покажет нам просто черную картинку. Самое время написать метод для градиента!
У меня получилось вот так:
drawGradient
public void drawGradient(int x1, int y1, int color1, int x2, int y2, int color2) {
float dx = x1 - x2; //Вспомогательные переменные
float dy = y1 - y2;
float AB = (float) Math.sqrt(dx * dx + dy * dy); //Вычисляется только один раз
//Перебираем все пиксели изображения
for (int y = 0; y < height; y++) {
for (int x = 0; x < width; x++) {
dx = x1 - x;
dy = y1 - y;
float AE2 = dx * dx + dy * dy;
float AE = (float) Math.sqrt(AE2);
dx = x2 - x;
dy = y2 - y;
float EB2 = dx * dx + dy * dy;
float EB = (float) Math.sqrt(EB2);
float p = (AB + AE + EB) / 2f;
float EF = 2 / AB * (float)Math.sqrt(Math.abs(p * (p - AB) *
(p - AE) * (p - EB)))
float EF2 = EF * EF;
float AF = (float) Math.sqrt(Math.abs(AE2 - EF2));
float BF = (float) Math.sqrt(Math.abs(EB2 - EF2));
if (AF + BF - 0.1f > AB) {
//Если пиксель лежит в зеленой или красной зоне
rgb[y * width + x] = AF < BF ? color1 : color2;
} else { //Рассчитываем цвет пикселя
float progress = AF / AB;
//Об методе interpolate речь пойдет дальше
rgb[y * width + x] = interpolate(color1, color2, progress);
}
}
}
}
/**
* @param num - число
* @return 0, если num < 0; 255, если num > 255; в остальных случаях num
*/
private static int clip(int num) {
return num <= 0 ? 0 : (num >= 255 ? 255 : num);
}
Обратите внимание что я применяю функцию модуля — Math.abs() везде, где есть хоть малейшая вероятность того, что в функцию нахождения квадратного корня — Math.sqrt() может попасть отрицательное число. В противном случае у нас появятся артефакты.
А в этой строке если убрать
- 0.1f, получается просто ужасное месиво. Из-за погрешности вычислений нам приходится отнимать небольшое число:if (AF + BF - 0.1f > AB) {
Осталось только разобраться с методом interpolate и дело в шляпе. Он должен принимать начальный цвет, конечный цвет и число progress, которое может быть от 0 до 1 и которое определяет долю каждого цвета. Например если progress = 0, возвращается начальный цвет, если progress = 1 — конечный цвет, а если progress = 0.5 — средний цвет между начальным и конечным. Задача ясна, метод написан:
interpolate
private int interpolate(int color1, int color2, float progress) {
//Разделяем оба цвета на составляющие
int a1 = (color1 & 0xff000000) >>> 24;
int r1 = (color1 & 0x00ff0000) >>> 16;
int g1 = (color1 & 0x0000ff00) >>> 8;
int b1 = color1 & 0x000000ff;
int a2 = (color2 & 0xff000000) >>> 24;
int r2 = (color2 & 0x00ff0000) >>> 16;
int g2 = (color2 & 0x0000ff00) >>> 8;
int b2 = color2 & 0x000000ff;
//И рассчитываем новые
float progress2 = (1 - progress);
int newA = clip((int) (a1 * progress2 + a2 * progress));
int newR = clip((int) (r1 * progress2 + r2 * progress));
int newG = clip((int) (g1 * progress2 + g2 * progress));
int newB = clip((int) (b1 * progress2 + b2 * progress));
//Собираем и возвращаем полученный цвет
return (newA << 24) + (newR << 16) + (newG << 8) + newB;
}
Давайте глянем на результат!
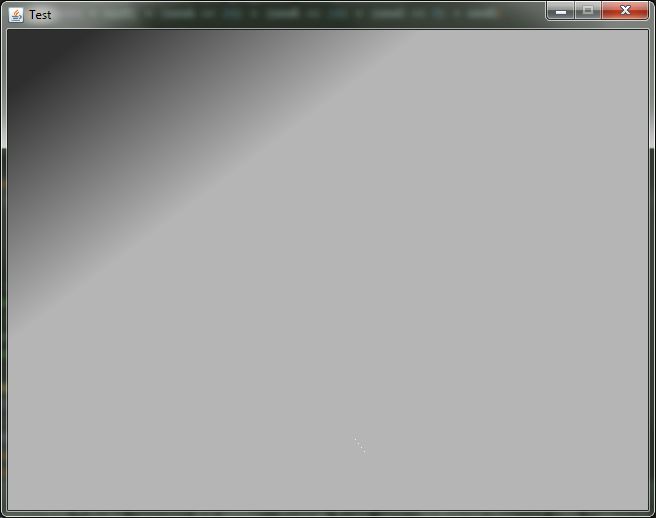
Уже неплохо, но наш использует линейную интерполяцию, а в фотошопе в ходу определенно какая-то другая.
Про интерполяции
Посмотрите внимательно на картинку. Левый градиент нарисован нашим алгоритмом, правый — фотошопом. На каждой строке стоит красная точка. И чем темнее строка, тем точка левее:

Как видно, линия у нас прямая, как рельса. Надо это исправлять. Вот тут я так ничего дельного не придумал и решил подсмотреть в интернете. Нашел статью на хабре, в которой описаны некоторые виды интерполяции и даже код есть: habrahabr.ru/post/142592
Ну что, реализуем косинусную интерполяция! Во первых добавим в класс EditableImage две константы:
public static final int INTERPOLATION_LINEAR = 0;
public static final int INTERPOLATION_COS = 1;
Во вторых перепишем немного метод interpolate, чтобы ему на вход подавалась одна из этих констант:
Скрытый текст
private int interpolate(int color1, int color2, float progress, int interpolation) {
//Разделяем оба цвета на составляющие
int a1 = (color1 & 0xff000000) >>> 24;
int r1 = (color1 & 0x00ff0000) >>> 16;
int g1 = (color1 & 0x0000ff00) >>> 8;
int b1 = color1 & 0x000000ff;
int a2 = (color2 & 0xff000000) >>> 24;
int r2 = (color2 & 0x00ff0000) >>> 16;
int g2 = (color2 & 0x0000ff00) >>> 8;
int b2 = color2 & 0x000000ff;
//И рассчитываем новые
float f;
if (interpolation == INTERPOLATION_LINEAR) {
f = progress;
} else if (interpolation == INTERPOLATION_COS) {
float ft = progress * 3.1415927f;
f = (1 - (float) Math.cos(ft)) * 0.5f;
} else {
throw new IllegalArgumentException();
}
int newA = clip((int) (a1 * (1 - f) + a2 * f));
int newR = clip((int) (r1 * (1 - f) + r2 * f));
int newG = clip((int) (g1 * (1 - f) + g2 * f));
int newB = clip((int) (b1 * (1 - f) + b2 * f));
//Собираем и возвращаем полученный цвет
return (newA << 24) + (newR << 16) + (newG << 8) + newB;
}
Затем в список параметров метода drawGradient добавим
int interpolation и в строчку вызова метода interpolate добавим эту переменную:rgb[y * width + x] = interpolate(color1, color2, progress , interpolation);
И в завершение в классе GradientPanel перепишем вызов метода drawGradient, добавив в него INTERPOLATION_COS
Вот что получилось с этим методом интерполяции:

Хм, выглядит неплохо, но в фотошопе линия явно не такая кривая. Что же делать? То слишком прямая, то слишком кривая… А что если сделать среднее из этих двух крайностей?
Отличная идея, добавляем константу
INTERPOLATION_COS_LINEAR = 2А в код метода interpolate добавляем еще один else if:
} else if (interpolation == INTERPOLATION_COS_LINEAR) {
float ft = progress * 3.1415927f;
f = (progress + (1 - (float) Math.cos(ft)) * 0.5f) / 2f;
}
И о чудо, получилась практически полная копия градиента из фотошопа!
Сами поглядите:

Наша слева.
А вот вам две картинки с верхнего скриншота, совмещенные в одну. Видно, что интерполяция практически одинаковая, отличия можно свалить на погрешности при округлениях:

Ура, мы сделали градиент как в фотошопе, хоть и гораздо более медленный.
Исходники и jar
На этом я заканчиваю первую часть. Во второй части я постараюсь оптимизировать алгоритм так круто, как только смогу. И реализую какой-нибудь готовый известный быстрый алгоритм рисования градиента, а потом сравню его по скорости со своим.
Кстати, если у вас есть на примете быстрые алгоритмы рисования градиентов, оставляйте их в комментариях.