Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
Хабр доступен 24/7 благодаря поддержке друзей
Комментарии 53
Просто потрясающе!
Нужна ли математика программисту?
Suicide mode ON
Нужен ли программист математике?
Ответ: Да, в частных случаях. В других частных случаях программисту нужна биохимия, экономика и куча других знаний необходимых для конкретного проекта.
Реально достали уже с этим «нужналипрограммистуматематика».
Реально достали уже с этим «нужналипрограммистуматематика».
Нужен ли этот вопрос здесь?
Нет, есть гугл.
Программист — он как профессор Мориарти — по определению математик!
Это офигенно!
Респект как от лица программиста, так и от лица математика!
Респект как от лица программиста, так и от лица математика!
Очень классно, спасибо. Иллюстрации отличные.
Это просто великолепно! Автор — молодец, Хабр — торт!
Круто. Ещё решить бы, как добиться решаемости сгенерированного лабиринта by design.
Не «пробивать» же «дырки» в «стенах», попутно натравливая на него всякие А*.
Не «пробивать» же «дырки» в «стенах», попутно натравливая на него всякие А*.
Этому вопросу посвящен целый раздел.
Попробую объяснить на пальцах: если запускать демо с теми параметрами, что указаны в посте (M = 0.065), то белые «извилины» (стены) никогда не будут сливаться. Поскольку изначально черная область была связна (из любой черной точки можно было дойти до любой другой черной точки, передвигаясь лишь по черным точкам), то и в любой другой момент времени она останется связной. Иначе говоря, решаемости лабиринта «by design» можно добиться правильным выбором параметров модели (точнее, одного параметра M).
Попробую объяснить на пальцах: если запускать демо с теми параметрами, что указаны в посте (M = 0.065), то белые «извилины» (стены) никогда не будут сливаться. Поскольку изначально черная область была связна (из любой черной точки можно было дойти до любой другой черной точки, передвигаясь лишь по черным точкам), то и в любой другой момент времени она останется связной. Иначе говоря, решаемости лабиринта «by design» можно добиться правильным выбором параметров модели (точнее, одного параметра M).
Спасибо за подробный ответ!
Поскольку изначально черная область была связна (из любой черной точки можно было дойти до любой другой черной точки, передвигаясь лишь по черным точкам), то и в любой другой момент времени она останется связной.
Только эта «связность» будет обеспечиваться наличием общей «внешней» оболочки, что несколько странно для лабиринта: они обычно обнесены стеной по периметру.
Вот немного пейнта по упомянутой картинке из статьи:
Хотя вот здесь все гораздо лучше:
Вот интересны границы интервала значений M, когда лабиринт будет терять связность либо вырождаться в белое либо чёрное пятно.
Надо поэкспериментировать и потом попробовать доказать.
Надо поэкспериментировать и потом попробовать доказать.
Тут скорее нужно не ломать стенки, а, наоброт, закрывать лишние дырки. Например, на самой первой картинке вариантов прохода от одной стены к другой слишком много. Вот тогда будет полная жесть :)
вот это хардкор!
О, извилины! Дефицит! Мне такие нужны!
Спасибо, красиво! Но что касается практичности, то главное свойство лабиринта – запутанность. В нем должен быть неочевидный правильный путь (или небольшое количество правильных путей, не считая петель и циклов), плюс большое количество тупиков или петель. А ваши лабиринты проходятся почти по прямой. Можно ли по-простому доработать алгоритм так, чтобы удлинить и запутать правильный путь?
Вы довольно точно смоделировали рост некоторых колоний бактерий, или, например, коралла-мозговика :)
Заглянул под кат с мыслью: «Что может быть необыкновенного в генерации лабиринта?», а тут такое… Снимаю шляпу, вы украли у меня часов 5 ночного сна!
*ушел генерировать лабиринты*
*ушел генерировать лабиринты*
Одна из тех очень немногих статей, ради которых я до сих пор и читаю хабр. По пальцам можно пересчитать их.
Благодарю за потрясающую иллюстрацию силы математики!
Спасибо за статью! Может быть, один лишь я не все понял, но все же: не могли бы вы пояснить, откуда берутся подобные формулы для сигмы: sigma = 1 / math.sqrt(2 * self.k) и sigma = 1 / math.sqrt(2 * self.m) и какую роль она выполняет?
В этом месте кода вычисляется свертка activity с весовой функцией
и с 
. В свою очередь, свертка с функцией по сути есть свертка с функцией Гаусса (с точностью до постоянного множителя):
Реализовывать такую операцию руками мне не хотелось, поэтому я представил ее в виде разности результатов двух сверток: с
и с . В свою очередь, свертка с функцией по сути есть свертка с функцией Гаусса (с точностью до постоянного множителя):Отсюда и берутся значения всех таинственных констант.
А мне кажется, или подобный результат возможен вообще без сложной математики?
Вот просто задавать несколько раз N точек, их движение, следить чтобы не сближались, вероятность разветвления, постепенное изменение угла движения.
Кажется очень просто.
Вот просто задавать несколько раз N точек, их движение, следить чтобы не сближались, вероятность разветвления, постепенное изменение угла движения.
Кажется очень просто.
Мне, как гуманитарию, это разрывает мозг. Многое непонятно, но понятно, что это потрясающе. Не смотря на то, что по математике у меня была уверенная пятерка, сложные формулы заставили лицо скривить гримасу ужаса от шока непонимания!
Статья хорошая, но является классическим примером советского образования.
Сначала идет куча математики, которую даже я, чертов Магистр Математики, вечером за пивком решил пролистать. Хорошо, что не закрыл. Ведь дальше идет как раз интересная часть. И так везде. На протяжении шести лет университета было ровно так же. Три месяца скучнейшей абстрактной математики, которая совершенно не понятно зачем нужна. А к моменту, когда начинается реальное применение, 95% студентов уже отвалилось и ничего не понимают.
Должно быть совершенно наоборот: показать в начале классное применение, упуская объяснение сложных моментов, а уже потом постепенно разворачивать сложность и ввожить новые абстракции и формулы.
Сначала идет куча математики, которую даже я, чертов Магистр Математики, вечером за пивком решил пролистать. Хорошо, что не закрыл. Ведь дальше идет как раз интересная часть. И так везде. На протяжении шести лет университета было ровно так же. Три месяца скучнейшей абстрактной математики, которая совершенно не понятно зачем нужна. А к моменту, когда начинается реальное применение, 95% студентов уже отвалилось и ничего не понимают.
Должно быть совершенно наоборот: показать в начале классное применение, упуская объяснение сложных моментов, а уже потом постепенно разворачивать сложность и ввожить новые абстракции и формулы.
Мои 4 курса ММФ кончились 10 лет назад (хоть я все же и Магистр, но Других Наук), но я испытал удовольствие от формул, хотя вообще-то далеко не с первого раза врубился. Суть ведь не в программе, так же? А чтобы самим делать подобное. Абстракция нужна чтобы иметь не единственное применение, и этот пост тому пример. И еще и мотивация.
Вы комент-то прочитали?
Переформулирую. Мысль в том, что практическая реализация — это дело второго приоритета. Проработать идею важнее.
К сожалению многие так и остались детьми — им интересно как машинка катается, а не как она устроена что бы кататься. Им это просто скучно и хочется смотреть на катающуюся машинку. Собственно поэтому вам и рекомендуют сначала сделать привлекательную презентацию с картинками и видео для альтернативно одаренных, а потом уже пугать формулами и проработкой идеи.
Тем более что модель Коши изучают в технических ВУЗах и фактически здесь мы видим отличный пятерочный курсач второкурсника физтеха или ВМК по мат методам.
Тем более что модель Коши изучают в технических ВУЗах и фактически здесь мы видим отличный пятерочный курсач второкурсника физтеха или ВМК по мат методам.
Спасибо за прекрасную статью. Вижу вы мучились с вставкой картинок с формулами. Советую стабильный онлайн сервис их генерации codecogs
Программирование великая вещь! Всего пару десятков строк кода и получается такая красотища. Мне этот метод генерации лабиринтов очень бы пригодился в одном проекте, но с python-ом я, к сожалению, не знаком. Если кто-нибудь возьмется портировать этот код на actionscript 3, то я буду не только благодарен, но и оплачу труды в размере 1000 руб. Кого это предложение интересует, пишите в личку.
Зарегистрируйтесь на Хабре, чтобы оставить комментарий
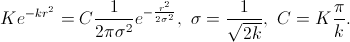
Необыкновенный способ генерации лабиринтов