В прошлой статье я писал про эвристические методы оптимизации перебора. В этой статье я расскажу вам о ещё одной, но уже асимптотической оптимизации — meet-in-the-middle.
Типичные для этого метода снижения асимптотики: и
и  .
.
Метод заключается в том, чтобы разделить задачу пополам, получить какие-то данные и сопоставить их друг с другом.
Meet-in-the-middle имеет смысл применять, если для конкретной задачи выполняются два условия:
1) Время обработки половины данных асимптотически меньше времени получения итогового ответа.
2) Известен асимптотически более быстрый способ получения ответа для всей задачи с использованием информации об обработки её половинок.
Чтобы появилось понимание, лучше всего посмотреть на примеры (даны в порядке увеличения предполагаемой сложности):
Дано N чисел. Надо выбрать k чисел так, чтобы их сумма была равна 0 (одинаковые элементы могут быть использованы несколько раз).
Наивное решение:
Перебрать все вариантов выбора k чисел, пересчитывая сумму по ходу рекурсии. Асимптотика:
вариантов выбора k чисел, пересчитывая сумму по ходу рекурсии. Асимптотика: 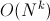 .
.
Решение с meet-in-the-middle для чётного k:
1) Мысленно разобьём k чисел, которые надо найти, на две кучки по k/2.
2.1) Выпишем все сумм.
сумм.
2.2) Отсортируем массив сумм.
2.3) Для каждой суммы s попытаемся найти бинарным поиском -s.
2.4) Если нашли, то вот он, наш ответ. Если нет, то такой комбинации не существует.
3) Profit: .
.
Изменить этот алгоритм для нечётного k, думаю, не составит труда для вас.
Если N = 30, а k = 12, то meet-in-the-middle будет работать примерно минуту, а наивный алгоритм — 17 лет.
У фокусника есть колода из 36 игральных карт. Изначально они лежат в порядке 1, 2, 3..., а он хочет получить какую-то конкретную перестановку, причем не более, чем за k шагов. На каждом шаге фокусник перекладывает m подряд идущих карт в начало колоды.
Задача состоит в том, чтобы узнать может ли он получить нужную перестановку.
Определим граф состояний S, как граф, в котором вершины задаются текущей перестановкой карт, а рёбра возможностью перейти от одной перестановки к другой за 1 шаг. Стоит отметить, что в этом графе 36! вершин, но из каждой вершины выходит 36-m+1 ребро, что относительно немного.
вершин, но из каждой вершины выходит 36-m+1 ребро, что относительно немного.
Наивное решение:
Запустить поиск в ширину на графе состояний S. Если дошли до нужного состояния или до вершины удалённой на k+1, то завершить поиск. Асимптотика: .
.
Решение с meet-in-the-middle:
1) Запустим два поиска в ширину из начальной и конечной вершины с максимальной глубиной k/2. Запишем два множества: все состояния, в которых побывали поиски в ширину.
2) Если эти множества пересекаются, значит есть путь, если нет, то и пути нет.
3) Profit: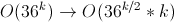 .
.
Надеюсь, я смог доходчиво объяснить концепцию meet-in-the-middle. Если остались вопросы — задавайте в комментариях, я постараюсь ответить. Спасибо за внимание.
Типичные для этого метода снижения асимптотики:
 и
и  .
.Вступление
Метод заключается в том, чтобы разделить задачу пополам, получить какие-то данные и сопоставить их друг с другом.
Meet-in-the-middle имеет смысл применять, если для конкретной задачи выполняются два условия:
1) Время обработки половины данных асимптотически меньше времени получения итогового ответа.
2) Известен асимптотически более быстрый способ получения ответа для всей задачи с использованием информации об обработки её половинок.
Чтобы появилось понимание, лучше всего посмотреть на примеры (даны в порядке увеличения предполагаемой сложности):
Пример №1: Оптимизация перебора
Дано N чисел. Надо выбрать k чисел так, чтобы их сумма была равна 0 (одинаковые элементы могут быть использованы несколько раз).
Наивное решение:
Перебрать все
 вариантов выбора k чисел, пересчитывая сумму по ходу рекурсии. Асимптотика:
вариантов выбора k чисел, пересчитывая сумму по ходу рекурсии. Асимптотика: 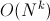 .
.Решение с meet-in-the-middle для чётного k:
1) Мысленно разобьём k чисел, которые надо найти, на две кучки по k/2.
2.1) Выпишем все
 сумм.
сумм.2.2) Отсортируем массив сумм.
2.3) Для каждой суммы s попытаемся найти бинарным поиском -s.
2.4) Если нашли, то вот он, наш ответ. Если нет, то такой комбинации не существует.
3) Profit:
 .
.Изменить этот алгоритм для нечётного k, думаю, не составит труда для вас.
Если N = 30, а k = 12, то meet-in-the-middle будет работать примерно минуту, а наивный алгоритм — 17 лет.
Пример №2: Оптимизация поиска кратчайшего пути в огромном графе состояний
У фокусника есть колода из 36 игральных карт. Изначально они лежат в порядке 1, 2, 3..., а он хочет получить какую-то конкретную перестановку, причем не более, чем за k шагов. На каждом шаге фокусник перекладывает m подряд идущих карт в начало колоды.
Картинка для пояснения

Задача состоит в том, чтобы узнать может ли он получить нужную перестановку.
Определим граф состояний S, как граф, в котором вершины задаются текущей перестановкой карт, а рёбра возможностью перейти от одной перестановки к другой за 1 шаг. Стоит отметить, что в этом графе 36!
 вершин, но из каждой вершины выходит 36-m+1 ребро, что относительно немного.
вершин, но из каждой вершины выходит 36-m+1 ребро, что относительно немного.Наивное решение:
Запустить поиск в ширину на графе состояний S. Если дошли до нужного состояния или до вершины удалённой на k+1, то завершить поиск. Асимптотика:
 .
.Решение с meet-in-the-middle:
1) Запустим два поиска в ширину из начальной и конечной вершины с максимальной глубиной k/2. Запишем два множества: все состояния, в которых побывали поиски в ширину.
2) Если эти множества пересекаются, значит есть путь, если нет, то и пути нет.
3) Profit:
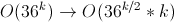 .
.Пример №3: Подсчёт количества «хороших» подмножеств
Для олимпиадников и тех, кто хочет поломать мозг
Дан граф G (N вершин). Требуется подсчитать количество полных подграфов графа G (клик).
Наивное решение:
Перебрать все подграфов и проверить за квадрат, что это клика. Асимптотика:
подграфов и проверить за квадрат, что это клика. Асимптотика:  .
.
Этот алгоритм можно улучшить до . Для этого нужно в рекурсивной функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда, не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за
. Для этого нужно в рекурсивной функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда, не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за 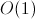 , используя побитовое «и» текущей маски и строчки матрицы смежности добавляемой вершины.
, используя побитовое «и» текущей маски и строчки матрицы смежности добавляемой вершины.
Решение с meet-in-the-middle.
1.1) Разбиваем граф G на 2 графа G1 и G2 по N/2 вершин. Находим за все клики в каждом из них. Асимптотика:
все клики в каждом из них. Асимптотика:  .
.
Теперь надо узнать для каждой клики графа G1 количество клик графа G2, таких, что их объединение — клика. Их сумма и есть итоговый ответ.
Так как для одной клики K графа G1 может быть несколько подходящих клик в G2, то воспользоваться тем же способом, что и в предыдущих двух примерах не получится. Но единственным объектом для клики K является маска вершин графа G2, которые ещё можно добавить. У нас есть куча времени для предподсчёта и этим нужно пользоваться: для каждой такой маски в G2 нужно предподсчитать ответ, а именно:
1.2) С помощью метода динамического программирования предподсчитаем для каждой маски вершин графа G2 количество клик, вершины которой являются подмножеством выбранной маски. Количество состояний: . Количество переходов:
. Количество переходов:  . Асимптотика:
. Асимптотика:  .
.
Вот пересчёт на языке Python:
2) Для каждой клики K (в том числе и пустой) графа G1 прибавим к глобальному ответу предподсчитанное количество клик, которые можно добавить к K (В том числе и пустых). Асимптотика: .
.
3) Profit: .
.
Наивное решение:
Перебрать все
 подграфов и проверить за квадрат, что это клика. Асимптотика:
подграфов и проверить за квадрат, что это клика. Асимптотика:  .
.Этот алгоритм можно улучшить до
 . Для этого нужно в рекурсивной функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда, не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за
. Для этого нужно в рекурсивной функции перебора хранить маску вершин, которые мы ещё можем добавить. Поддерживая эту маску, можно добавлять только «нужные» вершины, и тогда, не нужно будет в конце проверять подграф на то что он — клика. Добавлять вершину можно за 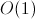 , используя побитовое «и» текущей маски и строчки матрицы смежности добавляемой вершины.
, используя побитовое «и» текущей маски и строчки матрицы смежности добавляемой вершины.Решение с meet-in-the-middle.
1.1) Разбиваем граф G на 2 графа G1 и G2 по N/2 вершин. Находим за
 все клики в каждом из них. Асимптотика:
все клики в каждом из них. Асимптотика:  .
.Теперь надо узнать для каждой клики графа G1 количество клик графа G2, таких, что их объединение — клика. Их сумма и есть итоговый ответ.
Так как для одной клики K графа G1 может быть несколько подходящих клик в G2, то воспользоваться тем же способом, что и в предыдущих двух примерах не получится. Но единственным объектом для клики K является маска вершин графа G2, которые ещё можно добавить. У нас есть куча времени для предподсчёта и этим нужно пользоваться: для каждой такой маски в G2 нужно предподсчитать ответ, а именно:
1.2) С помощью метода динамического программирования предподсчитаем для каждой маски вершин графа G2 количество клик, вершины которой являются подмножеством выбранной маски. Количество состояний:
 . Количество переходов:
. Количество переходов:  . Асимптотика:
. Асимптотика:  .
.Вот пересчёт на языке Python:
for mask in range(1 << N):
dp[mask] = 1 + sum([dp[mask & matrix[i]] for i in range(N) if ((mask & (1 << i)) > 0)])
2) Для каждой клики K (в том числе и пустой) графа G1 прибавим к глобальному ответу предподсчитанное количество клик, которые можно добавить к K (В том числе и пустых). Асимптотика:
 .
.3) Profit:
 .
.Заключение
Надеюсь, я смог доходчиво объяснить концепцию meet-in-the-middle. Если остались вопросы — задавайте в комментариях, я постараюсь ответить. Спасибо за внимание.