В данной статье будет показан математический подход к составлению алгоритмов на примере следующих вопросов и задач:
Итак, приступим.
Двоичным кодом Грея порядка n называется последовательность всех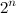 n-битных кодов, в которой любые два соседних кода различаются ровно в одном разряде.
n-битных кодов, в которой любые два соседних кода различаются ровно в одном разряде.
Пример кодов Грея порядка 2:
Нетрудно заметить, что такая последовательность не единственная(её как минимум можно обратить). Поэтому давайте разберемся в существовании двоичных кодов Грея других порядков и заодно выделим какой-то один вид таких последовательностей для дальнейшей работы.
Существование кодов Грея легко доказывается по индукции.
База — — пустая последовательность.
— пустая последовательность.
Переход. Пусть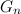 — последовательность кодов Грея порядка
— последовательность кодов Грея порядка 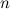 .
. 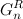 — последовательность
— последовательность 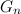 записанная в обратном порядке. Тогда последовательность
записанная в обратном порядке. Тогда последовательность 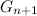 получается приписыванием нуля слева к каждому коду в последовательности
получается приписыванием нуля слева к каждому коду в последовательности 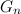 и единицы слева к каждому коду
и единицы слева к каждому коду 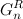 и последующим их объединением, т.е.
и последующим их объединением, т.е. 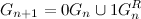 . Нетрудно проверить, что свойство кодов Грея в последовательности
. Нетрудно проверить, что свойство кодов Грея в последовательности 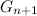 , построенную таким образом, не нарушается.
, построенную таким образом, не нарушается. 
Коды Грея, полученные таким способом, называются рефлексивными или симметрично отраженными. В дальнейшем мы будем рассматривать именно рефлексивные двоичные коды Грея.
В качестве упражнения выпишите симметрично отраженные коды Грея порядка 3 по приведенной в доказательстве формуле: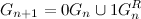 .
.
А теперь перейдем к приложению кодов Грея для решения некоторых задач комбинаторики.
Рассмотрим следующую задачу: «Дано множество из n элементов. Требуется вывести все его подмножества в таком порядке, что каждое следующее подмножество получается из предыдущего удалением или добавлением ровно одного элемента(т.е. в порядке минимального изменения).»
Будем считать, что элементы нашего множества пронумерованы от 1 до n. Тогда любому набору элементов множества можно поставить в соответствие n-битный двоичный код: если i-ый элемент множества входит в набор, то i-ый бит кода равен единице, иначе нулю. Таким образом, перебор всех подмножеств сводится к перебору двоичных кодов порядка n, а перебор подмножеств в порядке минимального изменения — к перебору двоичных кодов Грея.
Идея алгоритма рекурсивного перебора кодов Грея непременно следует из доказательства их существования, а именно приведенного в нем рекуррентного соотношения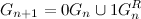 .
.
 Собственно, как и говорилось в доказательстве, код Грея порядка n получается из кода Грея порядка n-1 приписыванием нуля слева(этому соответствует вызов функции
Собственно, как и говорилось в доказательстве, код Грея порядка n получается из кода Грея порядка n-1 приписыванием нуля слева(этому соответствует вызов функции  и присвоение перед ним) и обратного кода Грея порядка n-1 приписыванием единицы слева(этому соответствует вызов функции
и присвоение перед ним) и обратного кода Грея порядка n-1 приписыванием единицы слева(этому соответствует вызов функции 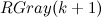 и присвоение перед ним).
и присвоение перед ним).
Перейдем к оценке сложности данного алгоритма. Очевидно, что дерево вызовов функции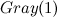 является полным двоичным деревом высоты n. Следовательно, общее число вызовов функции при генерации кодов Грея порядка n есть ни что иное, как
является полным двоичным деревом высоты n. Следовательно, общее число вызовов функции при генерации кодов Грея порядка n есть ни что иное, как 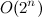 , что равно количеству всевозможных n-битных кодов. Следовательно, алгоритм оптимален.
, что равно количеству всевозможных n-битных кодов. Следовательно, алгоритм оптимален.
В качестве упражнения читателю предлагается проанализировать следующий, более короткий, алгоритм рекурсивного перебора.
Также хотелось бы сказать о существовании итеративного алгоритма перебора и других полезных свойствах кодов Грея, которые не рассматриваются в данной статье, и о которых можно узнать из других источников, например Википедии.
А теперь давайте перейдем к последней и самой интересной задаче.
Начнем с постановки задачи: «Дано множество из n элементов. Требуется вывести все его подмножества, состоящие ровно из k элементов, в таком порядке, что каждое следующее подмножество получается из предыдущего заменой ровно одного элемента(т.е. в порядке минимального изменения).»
Здесь сразу приходит в голову идея алгоритма из предыдущей задачи, но выводить мы будем только те коды Грея, в которых ровно k единиц. При этом возникает вопрос о корректности этого алгоритма: нам никто не гарантирует, что соседние коды в последовательности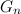 , в которой оставлены только двоичные коды с количеством единиц равным k, расположены в порядке минимального изменения — с разницей ровно в двух разрядах — получаются друг из друга заменой одного элемента. Поэтому перейдем к дальнейшему изучению свойств симметрично-отраженных кодов Грея.
, в которой оставлены только двоичные коды с количеством единиц равным k, расположены в порядке минимального изменения — с разницей ровно в двух разрядах — получаются друг из друга заменой одного элемента. Поэтому перейдем к дальнейшему изучению свойств симметрично-отраженных кодов Грея.
Введем некоторые обозначения:
 единицами в последовательности
единицами в последовательности 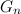 имеет вид
имеет вид 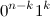 , а последний —
, а последний — 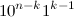 или
или  , если
, если 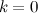 .
.
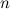 и
и  .
.
База —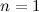 — верно(нетрудно проверить приведенные формулы для двух кодов 0 и 1).
— верно(нетрудно проверить приведенные формулы для двух кодов 0 и 1).
Переход. Пусть формулы верны для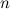 и любого
и любого 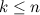 . Вспомним формулу из доказательства существования кодов Грея:
. Вспомним формулу из доказательства существования кодов Грея: 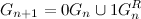 . Отсюда получим, что первый код с
. Отсюда получим, что первый код с 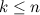 единицами в последовательности
единицами в последовательности 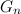 с приписанным слева нулем является первым кодом с
с приписанным слева нулем является первым кодом с  единицами в последовательности
единицами в последовательности 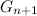 . При
. При 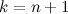 получим единственный код с
получим единственный код с 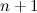 единицей, для которого формула также верна. При
единицей, для которого формула также верна. При 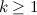 последний код с
последний код с  единицами в последовательности
единицами в последовательности 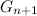 есть первый код с
есть первый код с  единицей и приписанной слева единицей в последовательности
единицей и приписанной слева единицей в последовательности 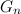 . При
. При 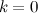 формула также верна.
формула также верна. 
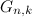 различаются ровно в двух разрядах.
различаются ровно в двух разрядах.
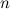 и
и  .
.
База —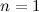 — очевидно(всего один возможный код в последовательности).
— очевидно(всего один возможный код в последовательности).
Переход. Пусть теорема верна для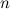 и
и 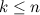 . При
. При 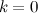 или
или 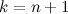 имеем всего один код в последовательности
имеем всего один код в последовательности 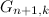 . При
. При 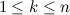 соседние слова находящиеся полностью в
соседние слова находящиеся полностью в 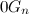 или в
или в 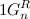 по индукционному предположению различаются ровно в двух разрядах. Остается проверить одну пару соседних кодов в
по индукционному предположению различаются ровно в двух разрядах. Остается проверить одну пару соседних кодов в 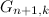 последний код с
последний код с  единицами в
единицами в 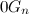 и первый код с
и первый код с  единицами в
единицами в 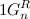 (последний с
(последний с  единицей в
единицей в 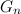 с приписанной слева единицей). По лемме, при
с приписанной слева единицей). По лемме, при 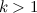 , они имеют вид
, они имеют вид 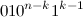 и
и 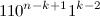 соответственно, а при
соответственно, а при 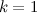 —
— 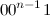 и
и 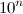 . Нетрудно видеть, что они различаются ровно в двух разрядах.
. Нетрудно видеть, что они различаются ровно в двух разрядах. 
Теперь мы можем сформулировать замечательные следствия из теоремы.
Эти следствия можно и нужно использовать для написания программы рекурсивного перебора подмножеств из k элементов в порядке минимального изменения.
 Хотелось бы обратить внимание на то, что вывод двоичного кода подразумевает еще и заполнение оставшихся разрядов единицами или нулями, в зависимости от значения u и v.
Хотелось бы обратить внимание на то, что вывод двоичного кода подразумевает еще и заполнение оставшихся разрядов единицами или нулями, в зависимости от значения u и v.
Перейдем к оценке сложности приведенного алгоритма. Заметим, что при углублении в рекурсию значение u всегда уменьшается. То есть мы сделаем не больше n углублений для достижения какого-то двоичного кода. Всего таких кодов —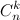 . Получаем итоговую асимптотику
. Получаем итоговую асимптотику 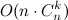 . Это довольно грубая оценка, но она всяко лучше
. Это довольно грубая оценка, но она всяко лучше 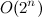 , особенно при величине k стремящейся к n: алгоритм практически линеен.
, особенно при величине k стремящейся к n: алгоритм практически линеен.
Легко заметить, что дерево вызовов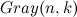 будет двоичным, но не будет полным. Проведем параллель оценки сложности в терминах деревьев: каждый лист соответствует получению какого-то двоичного кода, а расстояние до листа в дереве не превышает n. Оценка
будет двоичным, но не будет полным. Проведем параллель оценки сложности в терминах деревьев: каждый лист соответствует получению какого-то двоичного кода, а расстояние до листа в дереве не превышает n. Оценка 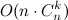 говорит нам о том, что мы просто просуммировали верхнюю оценку длин — n — всех путей до листов. Но ведь многие из этих путей имеют длину меньше n, а еще больше путей пересекаются друг с другом. Это должно наталкивать нас на мысль, что асимптотика приведенного алгоритма на самом деле намного лучше.
говорит нам о том, что мы просто просуммировали верхнюю оценку длин — n — всех путей до листов. Но ведь многие из этих путей имеют длину меньше n, а еще больше путей пересекаются друг с другом. Это должно наталкивать нас на мысль, что асимптотика приведенного алгоритма на самом деле намного лучше.
Точная оценка асимптотики — далеко не тривиальный факт, который можно найти в книге Э.Рейнгольда, Ю.Нивергельта и Н.Део «Комбинаторные алгоритмы. Теория и практика», либо попытаться доказать самому.
На этом хотелось бы закончить статью. Спасибо за внимание и до скорых встреч.
- Двоичные коды Грея. Их существование. Перебор подмножеств данного множества в порядке минимального изменения.
- Существование и реализация перебора подмножеств из k элементов в порядке минимального изменения.
Итак, приступим.
Двоичный код Грея
Двоичным кодом Грея порядка n называется последовательность всех
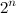 n-битных кодов, в которой любые два соседних кода различаются ровно в одном разряде.
n-битных кодов, в которой любые два соседних кода различаются ровно в одном разряде.Пример кодов Грея порядка 2:
- 00
- 01
- 11
- 10
Нетрудно заметить, что такая последовательность не единственная(её как минимум можно обратить). Поэтому давайте разберемся в существовании двоичных кодов Грея других порядков и заодно выделим какой-то один вид таких последовательностей для дальнейшей работы.
Существование
Существование кодов Грея легко доказывается по индукции.
База —
 — пустая последовательность.
— пустая последовательность.Переход. Пусть
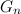 — последовательность кодов Грея порядка
— последовательность кодов Грея порядка 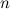 .
. 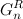 — последовательность
— последовательность 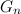 записанная в обратном порядке. Тогда последовательность
записанная в обратном порядке. Тогда последовательность 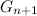 получается приписыванием нуля слева к каждому коду в последовательности
получается приписыванием нуля слева к каждому коду в последовательности 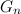 и единицы слева к каждому коду
и единицы слева к каждому коду 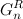 и последующим их объединением, т.е.
и последующим их объединением, т.е. 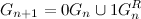 . Нетрудно проверить, что свойство кодов Грея в последовательности
. Нетрудно проверить, что свойство кодов Грея в последовательности 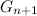 , построенную таким образом, не нарушается.
, построенную таким образом, не нарушается. 
Коды Грея, полученные таким способом, называются рефлексивными или симметрично отраженными. В дальнейшем мы будем рассматривать именно рефлексивные двоичные коды Грея.
В качестве упражнения выпишите симметрично отраженные коды Грея порядка 3 по приведенной в доказательстве формуле:
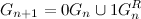 .
.А теперь перейдем к приложению кодов Грея для решения некоторых задач комбинаторики.
Перебор подмножеств данного множества в порядке минимального изменения
Рассмотрим следующую задачу: «Дано множество из n элементов. Требуется вывести все его подмножества в таком порядке, что каждое следующее подмножество получается из предыдущего удалением или добавлением ровно одного элемента(т.е. в порядке минимального изменения).»
Будем считать, что элементы нашего множества пронумерованы от 1 до n. Тогда любому набору элементов множества можно поставить в соответствие n-битный двоичный код: если i-ый элемент множества входит в набор, то i-ый бит кода равен единице, иначе нулю. Таким образом, перебор всех подмножеств сводится к перебору двоичных кодов порядка n, а перебор подмножеств в порядке минимального изменения — к перебору двоичных кодов Грея.
Идея алгоритма рекурсивного перебора кодов Грея непременно следует из доказательства их существования, а именно приведенного в нем рекуррентного соотношения
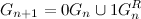 .
. Собственно, как и говорилось в доказательстве, код Грея порядка n получается из кода Грея порядка n-1 приписыванием нуля слева(этому соответствует вызов функции
Собственно, как и говорилось в доказательстве, код Грея порядка n получается из кода Грея порядка n-1 приписыванием нуля слева(этому соответствует вызов функции  и присвоение перед ним) и обратного кода Грея порядка n-1 приписыванием единицы слева(этому соответствует вызов функции
и присвоение перед ним) и обратного кода Грея порядка n-1 приписыванием единицы слева(этому соответствует вызов функции 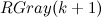 и присвоение перед ним).
и присвоение перед ним).Перейдем к оценке сложности данного алгоритма. Очевидно, что дерево вызовов функции
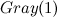 является полным двоичным деревом высоты n. Следовательно, общее число вызовов функции при генерации кодов Грея порядка n есть ни что иное, как
является полным двоичным деревом высоты n. Следовательно, общее число вызовов функции при генерации кодов Грея порядка n есть ни что иное, как 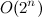 , что равно количеству всевозможных n-битных кодов. Следовательно, алгоритм оптимален.
, что равно количеству всевозможных n-битных кодов. Следовательно, алгоритм оптимален.В качестве упражнения читателю предлагается проанализировать следующий, более короткий, алгоритм рекурсивного перебора.
Пример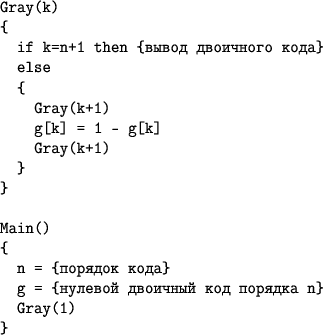

Также хотелось бы сказать о существовании итеративного алгоритма перебора и других полезных свойствах кодов Грея, которые не рассматриваются в данной статье, и о которых можно узнать из других источников, например Википедии.
А теперь давайте перейдем к последней и самой интересной задаче.
Перебор подмножеств из k элементов в порядке минимального изменения.
Начнем с постановки задачи: «Дано множество из n элементов. Требуется вывести все его подмножества, состоящие ровно из k элементов, в таком порядке, что каждое следующее подмножество получается из предыдущего заменой ровно одного элемента(т.е. в порядке минимального изменения).»
Здесь сразу приходит в голову идея алгоритма из предыдущей задачи, но выводить мы будем только те коды Грея, в которых ровно k единиц. При этом возникает вопрос о корректности этого алгоритма: нам никто не гарантирует, что соседние коды в последовательности
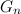 , в которой оставлены только двоичные коды с количеством единиц равным k, расположены в порядке минимального изменения — с разницей ровно в двух разрядах — получаются друг из друга заменой одного элемента. Поэтому перейдем к дальнейшему изучению свойств симметрично-отраженных кодов Грея.
, в которой оставлены только двоичные коды с количеством единиц равным k, расположены в порядке минимального изменения — с разницей ровно в двух разрядах — получаются друг из друга заменой одного элемента. Поэтому перейдем к дальнейшему изучению свойств симметрично-отраженных кодов Грея.Введем некоторые обозначения:
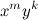 — строка, получаемая конкатенацией символа x (m раз) и конкатенацией символа y (k раз). Пример:
— строка, получаемая конкатенацией символа x (m раз) и конкатенацией символа y (k раз). Пример: 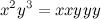 .
.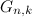 — последовательность всех n-битных кодов с k единицами, в которой коды идут в том порядке, в котором они расположены в последовательности
— последовательность всех n-битных кодов с k единицами, в которой коды идут в том порядке, в котором они расположены в последовательности 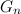 .
.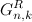 — последовательность всех n-битных кодов с k единицами, в которой коды идут в том порядке, в котором они расположены в последовательности
— последовательность всех n-битных кодов с k единицами, в которой коды идут в том порядке, в котором они расположены в последовательности 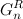 .
.
Лемма
Первый двоичный код с единицами в последовательности
единицами в последовательности 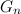 имеет вид
имеет вид 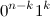 , а последний —
, а последний — 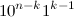 или
или  , если
, если 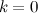 .
.Доказательство
Доказывать будем индукцией по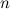 и
и  .
. База —
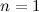 — верно(нетрудно проверить приведенные формулы для двух кодов 0 и 1).
— верно(нетрудно проверить приведенные формулы для двух кодов 0 и 1). Переход. Пусть формулы верны для
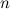 и любого
и любого 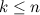 . Вспомним формулу из доказательства существования кодов Грея:
. Вспомним формулу из доказательства существования кодов Грея: 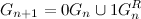 . Отсюда получим, что первый код с
. Отсюда получим, что первый код с 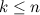 единицами в последовательности
единицами в последовательности 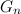 с приписанным слева нулем является первым кодом с
с приписанным слева нулем является первым кодом с  единицами в последовательности
единицами в последовательности 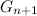 . При
. При 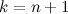 получим единственный код с
получим единственный код с 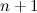 единицей, для которого формула также верна. При
единицей, для которого формула также верна. При 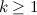 последний код с
последний код с  единицами в последовательности
единицами в последовательности 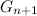 есть первый код с
есть первый код с  единицей и приписанной слева единицей в последовательности
единицей и приписанной слева единицей в последовательности 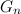 . При
. При 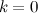 формула также верна.
формула также верна. 
Теорема
Соседние двоичные коды в последовательности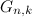 различаются ровно в двух разрядах.
различаются ровно в двух разрядах.Доказательство
Доказывать будем также индукцией по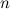 и
и  .
.База —
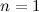 — очевидно(всего один возможный код в последовательности).
— очевидно(всего один возможный код в последовательности).Переход. Пусть теорема верна для
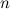 и
и 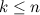 . При
. При 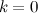 или
или 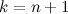 имеем всего один код в последовательности
имеем всего один код в последовательности 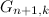 . При
. При 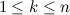 соседние слова находящиеся полностью в
соседние слова находящиеся полностью в 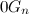 или в
или в 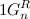 по индукционному предположению различаются ровно в двух разрядах. Остается проверить одну пару соседних кодов в
по индукционному предположению различаются ровно в двух разрядах. Остается проверить одну пару соседних кодов в 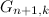 последний код с
последний код с  единицами в
единицами в 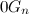 и первый код с
и первый код с  единицами в
единицами в 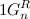 (последний с
(последний с  единицей в
единицей в 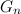 с приписанной слева единицей). По лемме, при
с приписанной слева единицей). По лемме, при 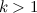 , они имеют вид
, они имеют вид 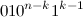 и
и 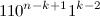 соответственно, а при
соответственно, а при 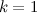 —
— 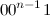 и
и 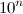 . Нетрудно видеть, что они различаются ровно в двух разрядах.
. Нетрудно видеть, что они различаются ровно в двух разрядах. 
Теперь мы можем сформулировать замечательные следствия из теоремы.
- Наивный алгоритм, предложенный ранее, корректен, то есть, если в последовательности
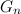 оставить только те двоичные коды, в которых ровно k единиц, то они будут расположены в порядке минимального изменения(каждый следующий получается из предыдущего заменой одного элемента).
оставить только те двоичные коды, в которых ровно k единиц, то они будут расположены в порядке минимального изменения(каждый следующий получается из предыдущего заменой одного элемента). - Последовательность
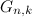 задается следующим рекуррентным соотношением:
задается следующим рекуррентным соотношением: 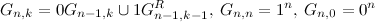 . Это можно проверить по индукции.
. Это можно проверить по индукции. - Последовательность
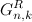 задается следующим рекуррентным соотношением:
задается следующим рекуррентным соотношением: 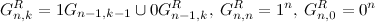 . Также проверяется по индукции.
. Также проверяется по индукции.
Эти следствия можно и нужно использовать для написания программы рекурсивного перебора подмножеств из k элементов в порядке минимального изменения.
 Хотелось бы обратить внимание на то, что вывод двоичного кода подразумевает еще и заполнение оставшихся разрядов единицами или нулями, в зависимости от значения u и v.
Хотелось бы обратить внимание на то, что вывод двоичного кода подразумевает еще и заполнение оставшихся разрядов единицами или нулями, в зависимости от значения u и v.Перейдем к оценке сложности приведенного алгоритма. Заметим, что при углублении в рекурсию значение u всегда уменьшается. То есть мы сделаем не больше n углублений для достижения какого-то двоичного кода. Всего таких кодов —
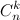 . Получаем итоговую асимптотику
. Получаем итоговую асимптотику 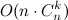 . Это довольно грубая оценка, но она всяко лучше
. Это довольно грубая оценка, но она всяко лучше 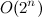 , особенно при величине k стремящейся к n: алгоритм практически линеен.
, особенно при величине k стремящейся к n: алгоритм практически линеен.Легко заметить, что дерево вызовов
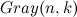 будет двоичным, но не будет полным. Проведем параллель оценки сложности в терминах деревьев: каждый лист соответствует получению какого-то двоичного кода, а расстояние до листа в дереве не превышает n. Оценка
будет двоичным, но не будет полным. Проведем параллель оценки сложности в терминах деревьев: каждый лист соответствует получению какого-то двоичного кода, а расстояние до листа в дереве не превышает n. Оценка 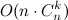 говорит нам о том, что мы просто просуммировали верхнюю оценку длин — n — всех путей до листов. Но ведь многие из этих путей имеют длину меньше n, а еще больше путей пересекаются друг с другом. Это должно наталкивать нас на мысль, что асимптотика приведенного алгоритма на самом деле намного лучше.
говорит нам о том, что мы просто просуммировали верхнюю оценку длин — n — всех путей до листов. Но ведь многие из этих путей имеют длину меньше n, а еще больше путей пересекаются друг с другом. Это должно наталкивать нас на мысль, что асимптотика приведенного алгоритма на самом деле намного лучше.Точная оценка асимптотики — далеко не тривиальный факт, который можно найти в книге Э.Рейнгольда, Ю.Нивергельта и Н.Део «Комбинаторные алгоритмы. Теория и практика», либо попытаться доказать самому.
На этом хотелось бы закончить статью. Спасибо за внимание и до скорых встреч.