 Речь здесь пойдёт о некоторых аспектах компьютерной безопасности, связанных с запутыванием кода программы. Именно это мне было интересно в связи с разработкой обфускатора .NET приложений – программы для защиты .NET кода от взлома. Есть и другая – тёмная сторона: запутыванием кода очень интересуются разработчики вирусов и других нехороших штук, но нам они неинтересны.
Речь здесь пойдёт о некоторых аспектах компьютерной безопасности, связанных с запутыванием кода программы. Именно это мне было интересно в связи с разработкой обфускатора .NET приложений – программы для защиты .NET кода от взлома. Есть и другая – тёмная сторона: запутыванием кода очень интересуются разработчики вирусов и других нехороших штук, но нам они неинтересны.Эмуляторы
Итак, Вы придумали супер алгоритм для запутывания кода программы. При декомпиляции код выглядит просто вырвиглазно и никто точно такое анализировать не будет. Казалось: победа! Но нет. Естественно обфусцированный код никто анализировать не будет… руками. Хакер поймёт как вы код запутывали и напишет «распутывалку». Если Ваш алгоритм был достаточно силён, то хакеру придётся писать собственный эмулятор, но и это не такая проблема как может показаться на первый взгляд – в сети есть доступные эмуляторы и даже специально написанные именно для целей взлома.
Из теории компьютерных наук известно, что не существует и никогда не будет существовать алгоритма, определяющего остановится ли программа или будет работать вечно – так называемая «проблема останова». Это гарантирует, что хакерский эмулятор, распутывающий обфусцированную программу, будет делать это как бы «локально»: он не сможет узнать состояние и значение всех переменных, задействованных в каждом участке кода и поэтому в точках условного ветвления часто будет полагать, что возможны все варианты хода программы. Вот тут-то на ум и приходит решение: запутанный код будет наполнен переходами по условиям, которые будут всегда истинны, но проэмулировать и понять это будет трудно. Примерно вот так:
if ((x+x & 1) == 0)
good_code
else
мусор
«Но это же как раз одна из тех запутывалок, которые хакер и собирается обходить с помощью эмулятора» — скажете Вы и будете правы. А что если придумать тысячу подобных фокусов? О, это решение, если у Вас есть легион программистов, каждый из которых придумывает трюки не похожие на трюки других. В реальности это не так. В реальности Вы думаете неделю и придумываете тридцать трюков, а хакер смотрит на код один день и находит все тридцать трюков, потому что тридцать – это не так уж много.
В области, связанной с запутыванием кода, тождественно истинные условные выражения называются «неявными предикатами» (оригинальный термин «opaque predicates»). Далее буду использовать слова «предикат» и «условие» как синонимы. Тема эта придумана давно и я, честно, не знаю кто исходный автор, должно быть фольклор. Несколько видных статей по предикатам:
- http://crypto.cs.mcgill.ca/~garboit/sp-paper.pdf
- citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.302.2312
- sandmark.cs.arizona.edu/ginger_pubs_talks/icecr7_paper.pdf
Идеальный генератор неявных предикатов
Сформулируем как должен выглядеть эдакий идеальный супер генератор неявных предикатов. Он создаёт предикаты P(x1,x2,…,xn), зависящие от переменных x1,x2,…,xn, причём может создавать как тождественно истинные, так и не всегда истинные предикаты в зависимости от желания пользователя генератора. И генератор обладает следующими фантастическими характеристиками:
- предикат генерируется за линейное время от длины;
- предикат очень похож на обычное условие из обычной программы (скрытность);
- не существует и не может существовать (!) алгоритма, который определял бы, что предикат сгенерирован нашим генератором;
- не существует и не может существовать (!) алгоритма, который по сгенерированному предикату мог бы определить всегда он истинный или существуют входные параметры на которых он ложный;
- не существует вероятностного алгоритма, который верно определял бы в среднем по меньшей мере в 80% случаев (цифра найдена методом научного тыка), является ли созданный генератором предикат тождественно истинным.
Теперь надо понять возможна ли хотя бы теоретически такая штука.
Пункт 4, похоже, возможен. Напомню, что Диофантово уравнение – это уравнение вида f(x1, x2, …, xn) = 0, где f — многочлен с целочисленными коэффициентами, а иксы — целые неотрицательные числа. Опять обращаясь к теории компьютерных наук, вспоминаем, что не существует и не может существовать алгоритма, который по любому Диофантову уравнению определял бы имеет оно решение или нет. В частности, по великой теореме Ферма, Диофантово уравнение (x+1)*(x+1)*(x+1) + (y+1)*(y+1)*(y+1) — (z+1)*(z+1)*(z+1) = 0 не имеет решений. Казалось: вот куда надо копать! Но не спешите. Диофантово уравнение – это вовсе не набор сумм и произведений интов со значениями от 0 до 4 млрд, а набор сумм и произведений целых чисел со значениями от 0 до бесконечности. Вам придётся записывать их с помощью так называемой «длинной арифметики» и выглядеть они будут в коде весьма странно.
Пункт 2 всем мешает. Интуитивно скрытным мы называем предикат, который не выделяется в толпе настоящих, «ненеявных» предикатов из настоящих программ. Умные люди уже проанализировали много типичных приложений и нашли, что большая часть предикатов в них совсем незамысловата: x == 0, x == y, x > 0 и т.д., где x, y – интовые переменные (во второй из приведённых выше статей умные люди как раз между делом анализируют условия типичных java программ). Не нужно долго гадать, чтобы понять, что условие скрытности очень важно для предикатов. Действительно, хакер может просто найти все «странные» предикаты и как-то обособить их или вообще удалить, что нам совсем не нужно.
Пункт 4 невозможен из-за пункта 2… хотя. Итак, если предикат является арифметическим и он «скрытен», то в нём скорее всего задействована только арифметика с интами, а значит существует алгоритм, который проверит является ли предикат всегда истинным: достаточно просто перебрать все значения интов, входящих в предикат. Но и это неплохо, ведь в лучшем случае для анализа предиката придётся перебрать 4 миллиарда значений! А если переменных в предикате две? Значит мы с чистой совестью, полагая, что P<NP, ослабим четвёртую характеристику генератора: задача выявления того факта, что созданный генератором предикат всегда истинен, должна быть NP-полной. Конечно, если окажется, что P=NP, то это тоже вряд ли вариант, но пока можно спать спокойно. Тут вспоминается 3-SAT – известная NP-полная задача, которую сам Бог велел вспомнить на этом моменте. Но предикаты, получающиеся на этом пути, едва ли можно назвать скрытыми.
Пункты 1, 3 и 5 обойдём молчанием – слишком тонкий вопрос для короткой статьи.
Граф выполнения программы
Арифметическими предикатами будем называть предикаты, вида f(x1,…,xn) < g(x1,…xn) или f(x1,…,xn) == g(x1,…,xn), где все иксы имеют тип инт, а f и g – обычные арифметические выражения. Почему же предикат должен быть обязательно арифметическим? Нет, не должен и даже не утверждаю, что в тексте ниже я смогу Вас убедить, что должен. Тем не менее приведу соображения, которые привели меня к мысли, что арифметические предикаты наиболее реальны.
Если задуматься, то понятно, что обфускация с помощью неявных предикатов преследует одну основную цель – запутывание графа выполнения программы. Граф выполнения – это единственный кусок информации, которые есть у нас на этапе обфускации и который отсутствует у хакера на этапе взлома. Выше мы выяснили, что действительно теоретически возможно необратимо запутать эту информацию.
Является ли арифметический предикат неявным (то есть всегда истинным)? Это NP-полная задача. На что указывает данный указатель в данном месте программы? Это неразрешимая задача, то есть нет общего алгоритма для решения такого вопроса, как и в случае проблемы останова. Вот и прекрасно: неразрешимая лучше, чем NP-полная. Следующая идея способа построения неявных предикатов почерпнута из второй статьи, приведённой выше (Collberg, Clark, Low).
Давайте, раз мы обладаем графом выполнения, раскидаем по программе незаметный код, строящий и модифицирующий где-то в памяти какую-то достаточно сложную динамическую структуру. Это действительно может быть незаметно: кто знает, что там потребовалось записать в память?
И мы будем знать в каждой конкретной точке программы каково состояние структуры и на что указывают содержащиеся в ней указатели.
На основе этих знаний мы втыкаем неявные предикаты и мёртвый код под неявными предикатами, который вызывает какие-то части программы, которые модифицируют нашу скрытую структуру.
В итоге хакер уже не обладает нашими знаниями о структуре, если только он не решит неразрешимую проблему разрешения указателей.
Рассмотрим игрушечный пример. Пусть часть исходного графа выполнения программы имеет вид:
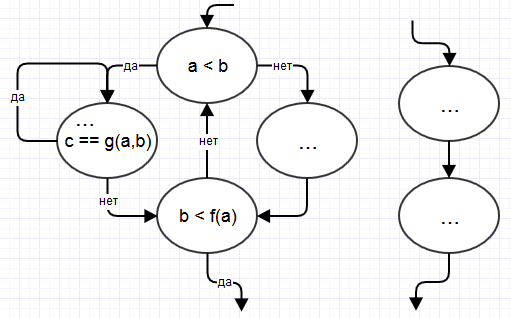
В обфусцированной программе мы формируем в памяти дико сложную структуру, состоящую из одного четырёхбайтового числа и указателя на это число. Пусть p – это указатель. Пусть при входе в левый нарисованный кусок графа (*p) гарантированно равно 1. Граф модифицируется так:
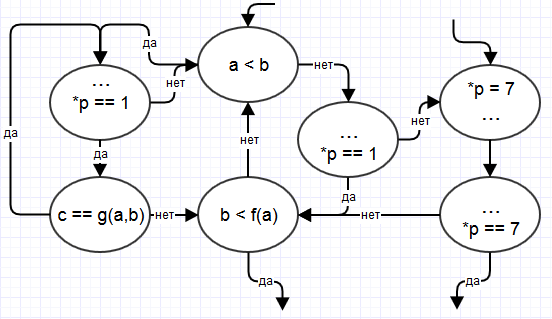
Если и раньше выяснение того, что *p == 1 могло быть сопряжено с трудностями, то теперь дополнительно можно сделать неверное предположение по этому куску, что иногда *p == 7 и в левой части рисунка.
Это хороший метод и он лучше, чем арифметические предикаты. Но есть одно большое НО: в реальности мы как и хакер не знаем граф выполнения. Всё этот подлый рефлекшн, коллбэки/делегаты и прочие непредсказуемые пути выполнения кода. А если код генерируется в памяти? Да, такое тоже бывает и особенно в .NET. Тем не менее мы знаем граф выполнения локально. В .NET, как минимум, можно быть уверенным в графе выполнения кода внутри каждого конкретного метода. Но если Вы вставите создание и построение некой структуры в памяти в каждый метод, то едва ли это будет скрытным. Вот так скрытность, а точнее её отсутствие, мешает нам использовать этот метод.
Есть и иные методы построения неявных предикатов, но все они (те, что я слышал краем уха) завязаны на графе выполнения всей программы и выглядят громоздко в контексте одного метода. Другое дело арифметические предикаты.
Реализация
В идеальном генераторе неявных предикатов есть ещё один большой плюс: алгоритм работы Вашего генератора не должен быть секретным! Наша реализация генератора, к сожалению, не совсем идеальна, и раскрывать всех деталей реализации нашего алгоритма мы пока не будем. Впрочем, я не нашёл у кого-то даже близкого к идеальному генератора. Тема очень интересная, и я был бы рад продолжить ее обсуждение в комментариях.
Ниже приведены некоторые результаты работы нашего генератора неявных предикатов. Выдержки из начала, середины и конца списка предикатов (3000 штук; приоритет операций как в с# ~; * / %; + -; « »; &; ^; |; все переменные int):
~x != x
(x + x & 1) == 0
(x + -x & 1) == 0
~x != x * 4u >> 2
(-x & 1) == (x & 1)
((-x ^ x) & 1) == 0
(x * 0x80 & 0x56) == 0
(x << 1 ^ 0x1765) != 0
~(-x * 0x40) != x << 6
(~(x * 0x80) & 0x3d) == 0x3d
x - 0x9d227fa9 != x - 0x699c945e
(y ^ y - 0x35f5f4d2) != 0x42a26409
(x * 0x20000000 & 0x19a27923) == 0
(int)(y * 9u + y * 0xf7u >> 3) >= 0
(x * 4 & 8) == (x + x * 3 - 0x1fef9d8f & 8)
(x | 0xffffdbe8) - 0x1baa != x || (x & 0x10) == 0x10
(x ^ 0x1145f) != 0 || (x | 0xfffeffff) == 0xffffffff
(uint)x / 0x59d7e3 != 0x90298cf9 || (x * 3 + x & 3) == 0
((uint)x % 0x38 + 0xe4df62c8 & 0x6d755e00) == 0x64554200
(x ^ 0x770363c6) != 0 || ((uint)x >> 0x19 ^ 0x926797eb) != 0
(uint)y / 0x2369af8 - 0x78400000 != (uint)x / 0x1f2ce * 0x10
(x & 0x8e3ef800) != 0x70641deb && (uint)x / 0x9388ea != 0x3ab6921c
Автор публикации: Дмитрий Косолобов, разработчик Appfuscator.