
Японский кроссворд — это известная головоломка, ответом которой является рисунок. Что это такое и как это решать, можно почитать на Википедии. Я хочу показать, как можно написать программу, которая будет решать японский кроссворд в системе Wolfram Mathematica путем перебора.
Основные идеи
Идея решения методом перебора заключается в том, чтобы создать списки всевозможных расположений клеток для всех строк и столбцов. После этого с помощью полученных списков найти те клетки, информация о которых будет точно известна. Затем отсеять такие расположения, которые противоречат найденной информации. Интуитивно понятно, что если циклически повторять последние две процедуры, то можно найти информацию о любой клетке. Итак, задачу можно разбить на три подзадачи:
- Составление всех возможных расположений.
- Поиск закрашенных и незакрашенных клеток.
- Удаление противоречащих расположений.
Поскольку Wolfram Mathematica создана для работы со списками, то и расположения клеток будут храниться в программе как списки. Будем обозначать информацию о клетках следующим образом:
- 1 — закрашенная клетка;
- 0 — незакрашенная клетка;
- * — клетка, о которой ничего не известно.
Например, снизу показаны эквивалентные список и расположение клеток:
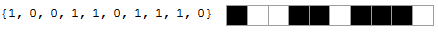
Составление всех возможных расположений
Немного теории
Рассмотрим конкретный пример. Необходимо найти всевозможные расположения для таких данных:

Выше показано одно из таких расположений. Как перебрать все возможные расположения?
Сделаем это следующим путем. Поставим в соответствие ключу (цифрам слева от поля) такие группы клеток:
{{1,0}, {1,1,0}, {1,1,1}}. Теперь создадим список, который будет хранить места, куда мы будем расставлять эти группы по порядку. В местах, куда мы будем ставить эти группы, будем хранить нули. Таким образом, получим список мест {0,0,0,0,0}. Расставляя группы клеток по порядку всеми способами на полученные места, как несложно убедиться, получим все требуемые расстановки для данных из задачи. Если поставить группы по порядку на места с номерами 1, 3, 4, то получится расположение из примера выше. Таким образом, получается, что все расположения равносильны сочетаниям из количества мест по количеству групп. Выбирая каким-нибудь образом места, куда ставить группы, мы получаем одно из возможных расположений. Для данных из примера количество расположений равно десяти.На вопросы «Почему в последней группе в конце нет нуля?» и «Почему мест именно пять?» сознательный читатель должен ответить сам.
Реализация
Понятно, что писать самому функцию, которая будет осуществлять перебор, особого желания нет, потому что в Mathematica существует встроенная функция
Subsets[list, {n}], которая это сделает. Она принимает список list как множество элементов и число n в качестве параметров и возвращает список подмножеств множества list длины n. Для нашего примера ее использование для перебора всех мест будет выглядеть так:In := Subsets[{1,2,3,4,5}, {3}]
Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}
Теперь напишем свою функцию, которая будет принимать число (длину поля
len, для данных примера — 10) и список (ключ clue, для данных примера — {1,2,3}) в качестве параметров и возвращать список всевозможных расположений. Будем все делать последовательно. Для начала создадим функцию, которая превращает число в список единиц. Для этого есть встроенная функция ConstantArray[c, n]; c — это элемент, которым заполняется список, а n — длина этого списка.In := ConstantArray[1, 2]
Out = {1, 1}
Далее, нам нужно присоединить ноль в конец этого списка. Это делается при помощи
Append[expr, elem]. Первый параметр — список, второй — то, что будем присоединять.In := Append[{1, 1}, 0]
Out = {1, 1, 0}
Соберем эти две функции в одну используя такой объект, как чистая функция (pure function). Это можно сделать двумя способами: либо
Function[arg, Append[ConstantArray[1, arg], 0], либо короче — Append[ConstantArray[1, #], 0]&.Теперь осталось применить эту функцию к каждому элементу списка, который соответствует ключу. Для этого есть очень полезная функция
Map[f, expr]. Она применяет функцию f к каждому элемента списка expr. У нее также есть короткий вариант: f /@ expr.In := Append[ConstantArray[1, #], 0]& /@ {1, 2, 3}
Out = {{1,0}, {1,1,0}, {1,1,1,0}}
Осталось только удалить ноль из последней группы. Тут поможет функция
Delete[expr, {i, j}]. Она удалит элемент из списка expr с индексом {i, j}. Не забываем, что последний элемент имеет индекс -1.In := Delete[{{1,0}, {1,1,0}, {1,1,1,0}}, {-1, -1}]
Out = {{1,0}, {1,1,0}, {1,1,1}}
Собранное все вместе выглядит так:
In := groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}]
Out = {{1,0}, {1,1,0}, {1,1,1}}
Со списком мест все понятно, но нам понадобится функция
Total[list], которая суммирует элементы списка list.In := positions = ConstantArray[0, len - Total[clue] + 1]
Out = {0,0,0,0,0}
Сейчас самое важное — это использование функции
Subsets. Плюс нам понадобится функция Range[n], которая возвращает список {1, 2, ..., n} и Length[list], которая дает длину списка list.In := sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}]
Out = {{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}}
Мы получили список мест, куда расставлять группы клеток. Теперь будем заниматься расстановкой. Для этого нам нужна функция
ReplacePart[expr, i->new], она заменяет в списке expr элемент с номером i на элемент new. Но для начала получим список замен, чтобы потом удобнее записать код. Это нам поможет сделать функция MapThread[f, {a1, a2, ...}, {b1, b2, ...}]. Результат ее выполнения будет следующим: {f[a1, b1], f[a2, b2], ...}. Итак, создаем список замен:In := rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub
Out = {{1->{1,0}, 2->{1,1,0}, 3->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 2->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {1->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {1->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 4->{1,1,1}}, {2->{1,0}, 3->{1,1,0}, 5->{1,1,1}}, {2->{1,0}, 4->{1,1,0}, 5->{1,1,1}}, {3->{1,0}, 4->{1,1,0}, 5->{1,1,1}}}
Финал всей затеи — это расстановка на свои места. Тут делаем
Flatten[list], который уберет лишние скобки:In := all = Flatten[ReplacePart[positions, #]]& /@ rep
Out = {{1,0,1,1,0,1,1,1,0,0}, {1,0,1,1,0,0,1,1,1,0}, {1,0,1,1,0,0,0,1,1,1}, {1,0,0,1,1,0,1,1,1,0}, {1,0,0,1,1,0,0,1,1,1}, {1,0,0,0,1,1,0,1,1,1}, {0,1,0,1,1,0,1,1,1,0}, {0,1,0,1,1,0,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}, {0,0,1,0,1,1,0,1,1,1}}
Вот и все, все расстановки получены. Осталось это все объединить в один модуль для удобства и мы получим требуемую функцию.
allPositions[len_, clue_] :=
Module[{groups, positions, sub, rep, all},
groups = Delete[Append[ConstantArray[1, #], 0]& /@ clue, {-1, -1}];
positions = ConstantArray[0, len - Total[clue] + 1];
sub = Subsets[Range[len - Total[clue] + 1], {Length[clue]}];
rep = MapThread[Function[{x, y}, x->y], {#, groups}]& /@ sub;
all = Flatten[ReplacePart[positions, #]]& /@ rep;
Return[all];]
Поиск закрашенных и незакрашенных клеток
Теперь среди всего этого добра, что мы получим, используя нашу функцию, нужно извлечь информацию о клетках. Пусть мы имеем некоторый список расположений. Если найдется такое место, где во всех расположениях стоит 1 либо 0, то это дает нам право утверждать, что на этой позиции всегда будет закрашенная либо, соответственно, незакрашенная клетка. На мой взгляд, самая простая реализация функции, которая будет это делать, состоит в следующем: все расположения суммируются поэлементно и в полученном списке ищутся либо числа, равные количеству всех расположений, либо нули. В первом случае эти числа меняются на единицы, а во втором — нули остаются на своих местах. Все остальные элементы заменяются звездочками. Для реализации воспользуемся функцией
ReplaceAll[list, rule]. Она заменит в списке list элементы в соответствии с правилами rule. Конструкция x_ /; x!=0 означает «элемент x, такой что x ≠ 0».findInformation[list_] := ReplaceAll[Total[list], {x_ /; x!=0 && x!=Length[list] -> "*", x_ /; x==Length[list] -> 1}]Для нашего примера работа функции выглядит так:
In := findInformation[allPositions[len, clue]]
Out = {*,*,*,*,*,*,*,1,*,*}
Восьмая клетка во всех расположениях будет закрашенная, поэтому и во всей сетке она будет закрашенная. Об остальных клетках ничего сказать нельзя.
Удаление противоречащих расположений
Полученную информацию можно использовать для того, чтобы отсеивать расположения, которые ей противоречат. Функция
DeleteCases[expr, pattern] будет нашим фильтром — она удаляет из списка expr все элементы, которые не удовлетворяют шаблону pattern. Также будет использоваться функция Except[c], которая выбирает все, кроме ее параметра.deleteFromList[list_, test_] := DeleteCases[list, Except[ReplaceAll[test, "*"->_]]]
Вернемся к примеру, пусть мы получили, что расположение клеток должно удовлетворять такому шаблону:
{*,*,0,0,*,1,0,*,*,*}. Запустив нашу функцию, получим:In := deleteFromList[allPositions[len, clue], {"*","*",0,0,"*",1,0,"*","*","*"}]
Out = {{1,0,0,0,1,1,0,1,1,1}, {0,1,0,0,1,1,0,1,1,1}}
Получилось, что из десяти расположений удовлетворяют шаблону только два.
Собираем все воедино. Финальный этап
Мы шаг за шагом создали все необходимые для решения кроссворда функции. Теперь важно все красиво собрать, чтобы получить решение. В качестве примера я использую кроссворд, взятый из киевского журнала японских кроссвордов «Релакс». Его автором является А. Леута.
Кроссворд задается в программу в виде списка ключей для строк и для столбцов.
rows = {{1}, {2}, {4}, {3,1}, {4,1}, {12}, {9}, {4,1}, {1,1,1,1,1}, {1,1,1,1}, {1,3,1}, {2,1,1}, {9,1}, {4,5,1}, {3,4,1}, {3,5,3}, {3,1,5}, {5,1,2}, {7,3}, {4,10}, {4,3,3}, {4,2,3}, {5,2,2}, {5,3,2}, {4,1,1,2}, {3,2,2}, {2,2}, {7}, {10}, {2,6}};
cols = {{3}, {6}, {8}, {13}, {1,12,1}, {2,7,2,1}, {5,2,7,4}, {5,3,12}, {8,2,3,1,1,2}, {8,2,1,3}, {2,3,4,1,4}, {2,2,1,1,5,3,5}, {4,6,7,2}, {2,3,3,8,2}, {1,2,2,2}, {1,4,1}, {2}, {2}, {9}, {1}};
Вводить размеры сетки не нужно, потому что и так их можно определить:
rowlength = Length[cols]
collength = Length[rows]
В программе рисунок будет храниться как список списков или обыкновенная матрица. Перед решением у нас нет информации вообще, поэтому каждый элемент ее будет звездочкой.
pic = ConstantArray["*", {collength, rowlength}];
Теперь самая громоздкая часть решения кроссворда — это наполнение списков всевозможных расположений. Тут нужно немного подождать.
rowpos = allPositions[rowlength, #]& /@ rows;
colpos = allPositions[collength, #]& /@ cols;
Когда все расположения заполнены, то можно приступать к решению. Идея такая: производится поиск по всем строкам закрашенных клеток и эти клетки записываются в основную сетку. Затем из расположений для столбцов удаляются те, которые противоречат полученной информации и ведется поиск по столбцам и т. д. Поиск будет проходить до тех пор, пока в сетке будет хотя бы одна звездочка; думаю, что работу цикла
While объяснять не нужно. MemberQ в приведенном коде возвращает True, если в сетке имеется звездочка и False в противоположном случае. Также используется транспонирование (Transpose) для того, чтобы можно было равноправно работать как со строками, так и со столбцами. Для вывода рисунка имеется встроенная функция ArrayPlot, которая закрашивает клетку черным, если в ней стоит 1 и белым, если 0 (звездочка закрашивается по умолчанию в коричневый цвет). Для того, чтобы видеть, как динамически меняется рисунок в процессе решения, используется Dynamic. Dynamic[ArrayPlot[pic, Mesh->True]]
While[MemberQ[pic, "*", 2],
pic = findInformation /@ rowpos;
colpos = MapThread[deleteFromList, {colpos, Transpose[pic]}];
pic = Transpose[findInformation /@ colpos];
rowpos = MapThread[deleteFromList, {rowpos, pic}];]
В результате получается вот такой рисунок:

Возможно, кто-то заметил, что решение является весьма неоптимальным. Да, это так, но не в оптимальности дело. Цель статьи — показать, что средствами Wolfram Mathematica можно удобно и быстро решить такую задачу. Но если уже говорить об оптимальности, то для этой задачи есть много способов оптимизации алгоритма, например, проводить отсеивание и поиск информации только в тех столбцах и строках, информация о клетках которых добавилась на предыдущем шагу, в данной версии программы поиск осуществляется во всех столбцах и строках.