
Введение
В моей предыдущей статье о методах машинного обучения без учителя был рассмотрен базовый алгоритм SOINN — алгоритм построения самоорганизующихся растущих нейронных сетей. Как было отмечено, базовая модель сети SOINN имеет ряд недостатков, не позволяющих использовать её для обучения в режиме lifetime (т.е. для обучения в процессе всего срока эксплуатации сети). К таким недостаткам относилась двухслойная структура сети, требующая при незначительных изменениях в первом слое сети переобучать второй слой полностью. Также алгоритм имел много настраиваемых параметров, что затрудняло его применение при работе с реальными данными.
В этой статье будет рассмотрен алгоритм An Enhanced Self-Organizing Incremental Neural Network, являющийся расширением базовой модели SOINN и частично решающий озвученные проблемы.
Общая идея алгоритмов класса SOINN
Основная идея всех алгоритмов SOINN заключается в построении вероятностной модели данных на основе предоставляемых системе образов. В процессе обучения алгоритмы класса SOINN строят граф, каждая вершина которого лежит в области локального максимума плотности вероятности, а ребра соединяют вершины, относящиеся к одним и тем же классам. Смысл такого подхода состоит в предположении, что классы образуют области высокой плотности вероятности в пространстве, и мы пытаемся построить граф, наиболее точно описывающий такие области и их взаимное расположение. Наилучшим образом эту идею можно проиллюстрировать следующим образом:
1)Для поступающих входных данных строится граф таким образом, чтобы вершины попадали в области локального максимума плотности вероятности. Так мы получаем граф, по каждой вершине которого мы можем построить некоторую функцию, описывающую распределение входных данных в соответствующей области пространства.
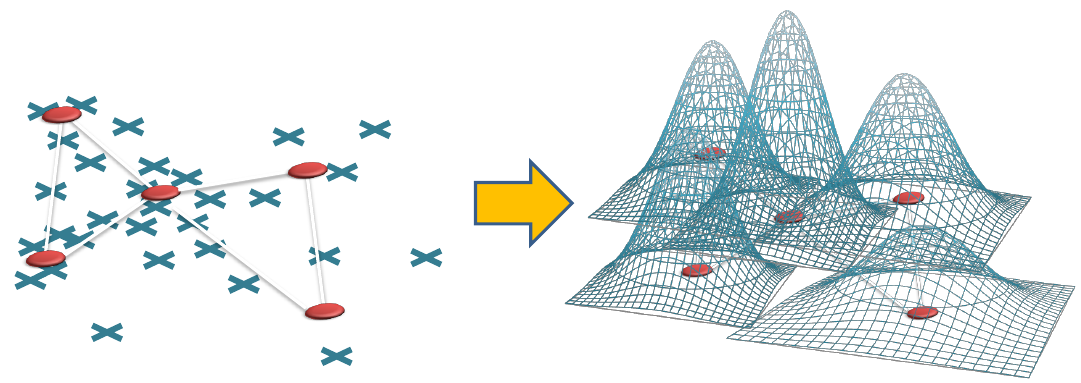
2)Граф в целом представляет собой смесь распределений, анализируя которую, можно определить число классов в исходных данных, их пространственное распределение и прочие характеристики.
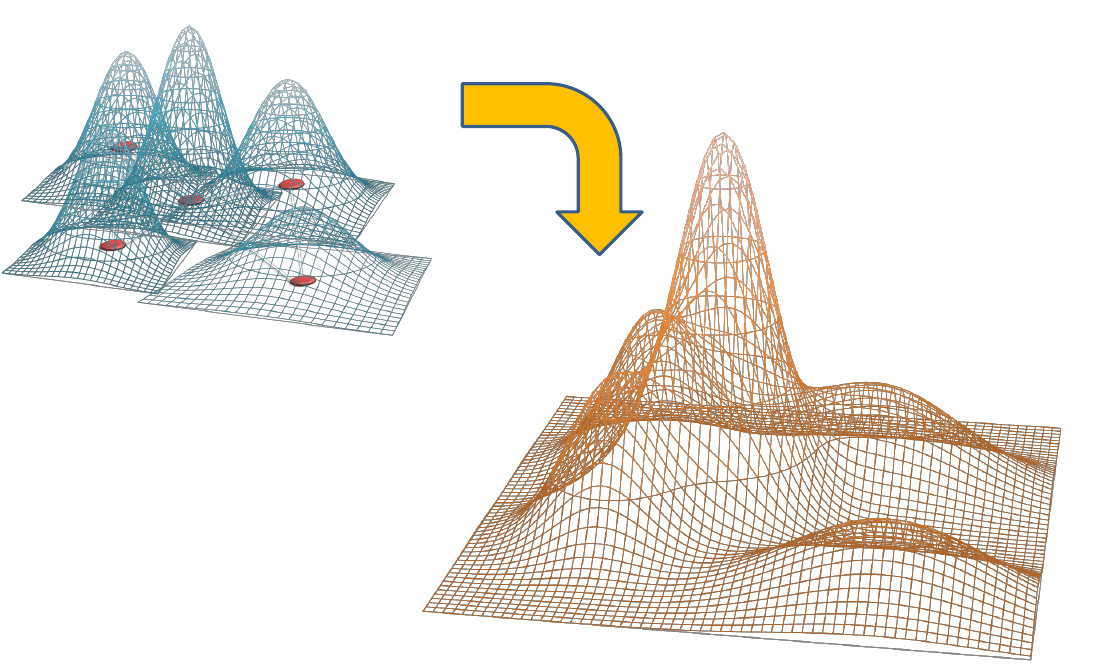
Алгоритм ESOINN
Теперь перейдем к рассмотрению алгоритма ESOINN. Как было уже сказано ранее, алгоритм ESOINN является производным от базового алгоритма обучения самоорганизующихся растущих нейронных сетей. Как и базовый алгоритм SOINN, рассматриваемый алгоритм предназначен для онлайн (и даже lifetime) обучения без учителя и без конечной цели обучения. Главным отличием ESOINN от рассмотренного ранее алгоритма является то, что структура сети тут однослойная и как следствие имеет меньшее число настраиваемых параметров и большую гибкость при обучении в процессе всего времени эксплуатации алгоритма. Также в отличие от базовой сети, где узлы-победители всегда соединялись ребром, в расширенном алгоритме появилось условие на создание связи, учитывающее взаимное расположение классов, к которым принадлежат узлы-победители. Добавление такого правила позволило алгоритму успешно разделять близкие и частично перекрывающие друг друга классы. Таким образом, алгоритм ESOINN пытается решать проблемы, выявленные у базового алгоритма SOINN.
Далее будет детально рассмотрен алгоритм построения сети ESOINN.
Блок схема алгоритма
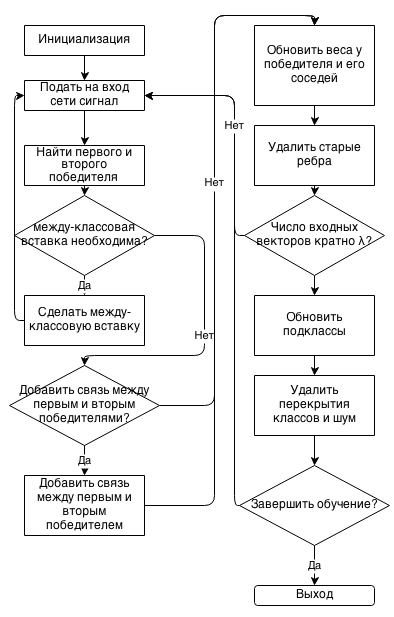
Описание алгоритма
Используемые обозначения
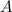 — набор узлов графа.
— набор узлов графа.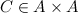 — набор ребер графа.
— набор ребер графа.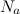 — число узлов в
— число узлов в 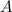 .
.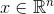 — вектор признаков объекта, поданного на вход алгоритма.
— вектор признаков объекта, поданного на вход алгоритма.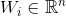 — вектор признаков i-й вершины графа.
— вектор признаков i-й вершины графа.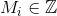 — число накопленных сигналов i-й вершины графа.
— число накопленных сигналов i-й вершины графа.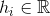 — плотность в i-й вершине графа.
— плотность в i-й вершине графа.Алгоритм
- Инициализировать набор узлов
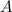 двумя узлами с векторами признаков взятыми случайным образом из области допустимых значений.
двумя узлами с векторами признаков взятыми случайным образом из области допустимых значений.
Инициализировать набор связей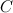 пустым множеством.
пустым множеством.
- Подать на вход вектор признаков входного объекта
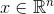 .
.
- Найти ближайший узел
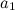 (победитель) и второй ближайший узел
(победитель) и второй ближайший узел 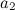 (второй победитель), как:
(второй победитель), как:
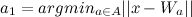
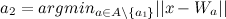
- Если расстояния между вектором признаков входного объекта и
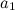 или
или 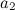 больше некоторого заданного порога
больше некоторого заданного порога 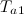 или
или 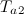 , то он порождает новый узел (Добавить новый узел в
, то он порождает новый узел (Добавить новый узел в 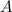 и перейти на шаг 2).
и перейти на шаг 2).
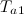 и
и 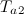 вычисляются по формулам:
вычисляются по формулам:
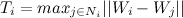 (если вершина имеет соседей)
(если вершина имеет соседей)
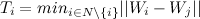 (если вершина не имеет соседей)
(если вершина не имеет соседей)
- Увеличить возраст всех ребер исходящих из
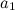 на 1.
на 1.
- Используя Алгоритм 2, определить, нужна ли связь между
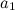 и
и 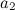 :
:
- Если необходимо: если ребро
 существует, то обнулить его возраст, иначе создать ребро
существует, то обнулить его возраст, иначе создать ребро  и установить его возраст равным 0.
и установить его возраст равным 0.
- Если в этом нет необходимости: если ребро существует, то удалить его.
- Если необходимо: если ребро
- Увеличить число накопленных победителем сигналов по формуле:
 .
.
- Обновить плотность победителя по формуле:
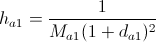 , где
, где 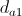 — средняя дистанция между узлами внутри кластера, к которому принадлежит победитель. Она вычисляется по формуле:
— средняя дистанция между узлами внутри кластера, к которому принадлежит победитель. Она вычисляется по формуле: 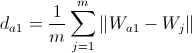 .
.
- Адаптировать вектора признаков победителя и его топологических соседей с весовыми коэффициентами
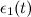 и
и 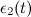 по формулам:
по формулам:
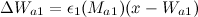
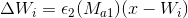
Мы применяем ту же схему адаптации, что и в базовом алгоритме SOINN:
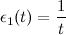
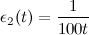
- Найти и удалить те ребра, чей возраст превышает некоторое пороговое значение
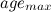 .
.
- Если число входных сигналов, генерируемых до сих пор, кратно некоторому параметру
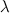 , то:
, то:
- Обновить метки классов для всех узлов, используя Алгоритм 1.
- Удалить узлы, являющиеся шумом, следующим образом:
- Для всех узлов
 из
из 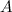 : если узел имеет двух соседей и
: если узел имеет двух соседей и 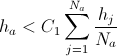 , то удалить этот узел.
, то удалить этот узел.
- Для всех узлов
 из
из 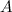 : если узел имеет одного соседа и
: если узел имеет одного соседа и 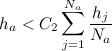 , то удалить этот узел.
, то удалить этот узел.
- Для всех узлов
 из
из 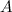 : если узел не имеет соседей, то удалить его.
: если узел не имеет соседей, то удалить его.
- Для всех узлов
- Обновить метки классов для всех узлов, используя Алгоритм 1.
- Если процесс обучения закончен, то классифицировать узлы различных классов (используя алгоритм выделения связанных компонент графа), а затем сообщить число классов, прототип-вектор для каждого класса и остановить процесс обучения.
- Перейти на шаг 2 для продолжения обучения без учителя, если процесс обучения еще не закончен.
Алгоритм 1: Разделение композитного класса на подклассы
- Назовем узел вершиной класса, если он имеет максимальную плотность в окрестности. Найти все такие вершины в составном классе и присвоить им различные метки.
- Отнести остальные вершины к тем же классам, что и у соответствующих им вершин.
- Узлы лежат в области перекрытия классов, если они принадлежат разным классам и имеют общее ребро.
На практике такой способ разделения класса на подклассы приводит к тому, что при наличии шумов большой класс может быть ложно классифицирован как несколько небольших классов. Поэтому, прежде чем разделить классы, необходимо сгладить их.
Предположим, что у нас есть два несглаженных класса:
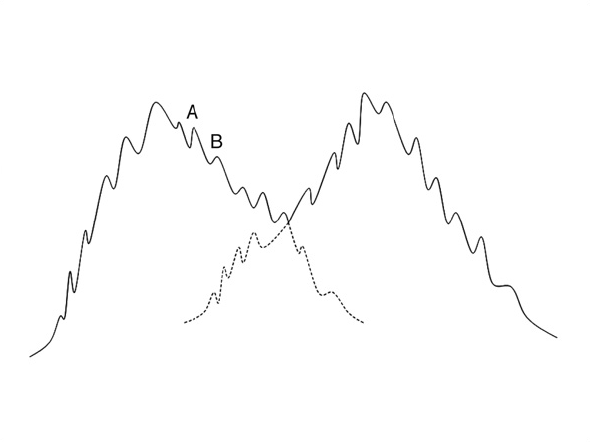
Возьмем подкласс
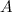 и подкласс
и подкласс 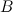 . Предположим, что плотность вершины подкласса
. Предположим, что плотность вершины подкласса 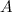 равна
равна 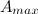 , а у подкласса
, а у подкласса 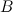 равна
равна 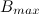 . Объединим
. Объединим 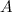 и
и 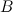 в один подкласс в том случае, если выполняются следующие условия:
в один подкласс в том случае, если выполняются следующие условия: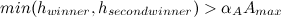
или
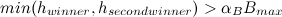
Здесь первый и второй победитель лежат в области перекрытия подклассов
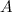 и
и 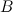 . Параметр
. Параметр 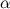 вычисляется следующим образом:
вычисляется следующим образом: 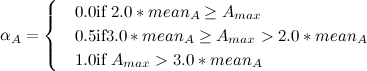 , где
, где 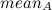 — средняя плотность узлов в подклассе
— средняя плотность узлов в подклассе 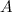 .
.После этого удалим все ребра, соединяющие вершины различных классов. Таким образом мы разделяем композитный класс на подклассы, не перекрывающие друг друга.
Алгоритм 2: Построение связи между вершинами
Соединим два узла в том случае, если:
- Хотя бы один из них является новым узлом (еще не определено, к какому подклассу он относится).
- Они принадлежат одному классу.
- Они принадлежат различным классам, и при этом выполняются условия на слияние этих классов (условия из Алгоритма 1).
Иначе не соединяем эти узлы, а если связь между ними существует, то удаляем её.
Благодаря использованию Алгоритма 1 при проверке необходимости создать ребро между узлами, алгоритм ESOINN будет стараться найти «баланс» между излишним разделением классов и объединением различных классов в один. Это свойство позволяет успешно проводить кластеризацию близко расположенных классов.
Обсуждение алгоритма
Используя показанный выше алгоритм, мы вначале находим пару вершин с ближайшими к входному сигналу векторами признаков. Затем мы решаем, относится ли входной сигнал к одному из уже известных классов или это представитель нового класса. В зависимости от ответа на этот вопрос мы либо создаем в сети новый класс, либо корректируем уже известный, соответствующий входному сигналу класс. В том случае, если процесс обучения длится уже достаточно большое время, сеть корректирует свою структуру, разделяя непохожие и объединяя похожие подклассы. После того, как обучение закончено, мы классифицируем все узлы к различным классам.
Как можно заметить, в процессе своей работы сеть может обучаться новой информации, при этом не забывая всё то, что она изучила ранее. Это свойство позволяет в некоторой мере решить дилемму стабильности-пластичности и делает сеть ESOINN пригодной для lifetime обучения.
Эксперименты
Для проведения экспериментов с представленным алгоритмом, он был реализован на языке C++ с применением библиотеки Boost Graph Library. Код выложен на GitHub.
В качестве площадки для проведения экспериментов был исопльзован конкурс, по классификации рукописных цифр на базе MNIST, на сайте kaggle.com. Тренировочные данные содержат 48000 изображений рукописных цифр размером 28x28 пикселей и имеющих 256 оттенков серого, представленных в виде 784-мерных векторов.
Результаты классификации мы получали в нестационарной среде(т.е. в процессе классификации тестовой выборки сеть продолжала обучаться).
Параметры сети были взяты следующим образом:
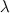 = 200
= 200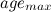 = 50
= 50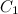 = 0.0001
= 0.0001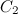 = 1.0
= 1.0В результате работы, сеть выделила 14 кластеров, центры которых выглядят следующим образом:

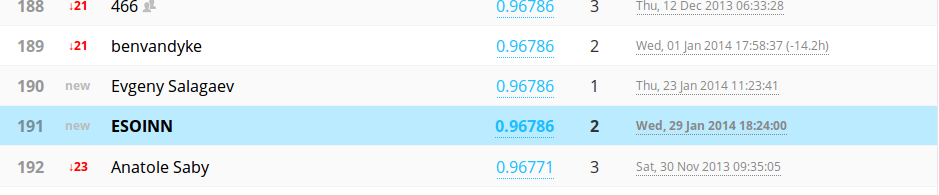
На момент написания статьи, ESOINN занимал почетное 191 место в рейтинге с точностью 0.96786 на 25% тестовой выборки, что не так уж и плохо для алгоритма изначально не имеющего никакой априорной информации о входных данных.
Заключение
В этой статье был рассмотрен модифицированный алгоритм обучения растущих нейронных сетей ESOINN. В отличие от базового алгоритма SOINN, алгоритм ESOINN имеет только один слой и может быть использован для lifetime обучения. Также, алгоритм ESOINN позволяет работать с частично перекрывающимися и размытыми классами, чего не умела базовая версия алгоритма. Число параметров алгоритма было снижено вдвое, что позволяет проще настраивать сеть при работе с реальными данными. Эксперимент показал работоспособность рассмотренного алгоритма.
Литература
- «An enhanced self-organizing incremental neural network for online unsupervised learning» Shen Furaoa, Tomotaka Ogurab, Osamu Hasegawab, 2007.
- A talk on SOINN delivered by Osamu Hasegawa from Tokyo Institute of Technology at IIT Bombay.
- A talk on SOINN delivered by Osamu Hasegawa from Tokyo Institute of Technology at IIT Bombay(video).
- Сайт лаборатории Hasegawa Lab, занимающейся исследованиями самоорганизующихся растущих нейронных сетей.