В данной статье будет рассказано и показано, как применять среду Wolfram Mathematica к решению сложных систем дифференциальных уравнений, графической интерпретации результатов решения, применения элементов процедурного программирования к физическим задачам, на примере движения твёрдого тела. Суть статьи в том, что бы показать, как с помощью средств компьютерной алгебры легко и просто проводить анализ сложных физических систем, которые будоражили умы физиков XIX века.
Сферическое движение — движение ТТ, имеющего одну неподвижную точку. Каждая из точек ТТ при таком движении перемещается по поверхности сферы с центром в точке закрепления. В таком случае говорят о вращательном движении, которое слагается из серии элементарных поворотов вокруг мгновенных осей вращения, проходящих через точку закрепления. Мгновенная ось вращения непрерывно изменяет своё положение, как по отношению к системе отсчёта, в которой рассматривается движение, так и в самом теле, образуя при этом две канонические поверхности, называемые соответственно неподвижным и подвижным аксоидами.
ТТ с неподвижной точкой имеет 3 степени свободы, и его положение по отношению к данной системе отсчёта определяется тремя параметрами, а точнее углами Эйлера. Эти углы определяют три поворота системы, которые позволяют привести любое положение системы к текущему.
Если взять элементарные повороты СК вокруг осей Z и X в порядке Z, X', Z'' на соответствующие углы Ψ, θ и φ, то такое преобразование приводит к выражению матрицы поворота через углы Эйлера. С помощью такой матрицы, происходит поворот ТТ в пространстве.

Применяемые углы имеют следующий физический смысл:
Сферическое движение ТТ, впервые описанное Леонардом Эйлером (нем. Leonhard Euler) имеет решение только в трёх случаях:
Далее будем говорить о движение тяжелого симметричного волчка в случае Лагранжа.
Построим рисунок тяжелого симметричного волчка в поле сил тяжести. Роль волчка отведём конусу.
Уравнения движения получим из теоремы о кинетическом моменте, предварительно записав его в общей форме в подвижной СК.
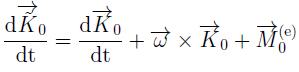
Теперь воспользуемся построенным нами рисунком и записанной теоремой: опуская нудные формулы, учтём моменты инерции симметричного волчка и приводя подобные получаем систему уравнений движения ТТ в поле сил тяжести.
Данная система не решается строго аналитически, а решение представляется только в квадратурах. Мы же решим эту систему численно и проанализируем полученные результаты.
Для начала нам необходимо задать начальные условия нашей системе ДУ: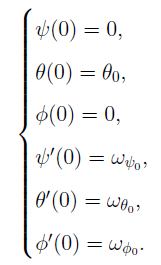
Далее, с помощью возможностей системы компьютерной алгебры, зададим параметры волчка, нарисуем примитивы и решим численно систему ДУ.
Затем получим матрицу поворота, о которой мы говорили ранее, встроенными средствами языка, подставим туда численное решение и применим к этому «торту» оператор геометрической трансформации:

Вот в принципе и все сложности решения в пару строк. Осталось только определить графическую область, построить траекторию движения и сделать анимацию, но это уже, как говорится на любителя (можно ограничится и численным выводом матриц преобразования). Оставшаяся часть кода:
Вывод результатов программы осуществляется в виде окна с динамическими параметрами начальных условий движения, времени анимации и прозрачностью волчка.
Проанализируем поведение волчка в случае регулярной (вынужденной) прецессии в поле сил тяжести:
Согласно теореме о кинетическом моменте (мы говорили о ней выше), за каждый малый промежуток времени dt вектор момента импульса получает под действием силы тяжести приращение , направленное вдоль
, направленное вдоль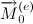 , т.е. лежащее в горизонтальной плоскости перпендикулярно оси волчка. Отсюда следует, что вектор момента импульса и вместе с ним ось волчка равномерно поворачиваются (совершают прецессию) вокруг вертикали, проходящей через точку опоры. Наклоненный к вертикали волчок прецессирует, т.е. помимо вращения вокруг собственной оси поворачивается еще и вокруг вертикальной оси. При быстром собственном вращении эта прецессия (поворот вокруг вертикальной оси) происходит настолько медленно, что с хорошей точностью можно пренебречь той составляющей момента импульса, которая обусловлена прецессией вокруг вертикали. Такое поведение оси волчка называют регулярной прецессией. Это вынужденная прецессия, так как она происходит под действием момента силы тяжести. Все точки волчка, лежащие на его оси, равномерно движутся по круговым траекториям, центры которых лежат на вертикали, проходящей через точку опоры волчка. На рисунке приведена иллюстрация регулярной прецессии волчка.
, т.е. лежащее в горизонтальной плоскости перпендикулярно оси волчка. Отсюда следует, что вектор момента импульса и вместе с ним ось волчка равномерно поворачиваются (совершают прецессию) вокруг вертикали, проходящей через точку опоры. Наклоненный к вертикали волчок прецессирует, т.е. помимо вращения вокруг собственной оси поворачивается еще и вокруг вертикальной оси. При быстром собственном вращении эта прецессия (поворот вокруг вертикальной оси) происходит настолько медленно, что с хорошей точностью можно пренебречь той составляющей момента импульса, которая обусловлена прецессией вокруг вертикали. Такое поведение оси волчка называют регулярной прецессией. Это вынужденная прецессия, так как она происходит под действием момента силы тяжести. Все точки волчка, лежащие на его оси, равномерно движутся по круговым траекториям, центры которых лежат на вертикали, проходящей через точку опоры волчка. На рисунке приведена иллюстрация регулярной прецессии волчка.
Данное событие происходит только при строго определенных начальных условиях.
Теперь можно перейти к исследованию вопроса о том, как будет вести себя вращающийся волчок под действием силы тяжести при начальных условиях, не обеспечивающих немедленного возникновения регулярной прецессии. В общем случае движение волчка должно представлять собой суперпозицию вынужденной регулярной прецессии и нутации, что отображено на рисунке.
В первый момент, как только мы отпускаем ось волчка, под действием силы тяжести она действительно начинает падать вниз, что вполне согласуется с нашими интуитивными представлениями. Но по мере того, как ось набирает скорость, траектория ее верхнего конца все сильнее отклоняется от вертикали. Вскоре движение оси становится горизонтальным, как и при регулярной прецессии, но скорость этого движения больше той, что нужна для регулярной прецессии. Траектория конца оси начинает отклоняться вверх. Поднявшись до исходной высоты, ось «замирает» – ее скорость обращается в нуль. Затем все повторяется сначала. Но теперь мы понимаем, что такое своеобразное поведение, когда конец оси движется по циклоидальной траектории, объясняется сложением двух движений – нутации волчка вокруг вектора момента импульса с одновременной вынужденной прецессией этого вектора вокруг вертикали.
Когда нутации малы, вынужденную прецессию называют псевдорегулярной, на рисунке можем наблюдать данное явление. Для быстро вращающихся гироскопов(т.е. очень быстро вращающихся волчков), применяемых в технике, псевдорегулярная прецессия практически не отличается от регулярной. В таких случаях нутация проявляет себя как едва заметное мелкое и частое дрожание оси гироскопа. Кроме того, мелкомасштабные нутации быстро затухают под действием сил трения, и псевдорегулярная прецессия переходит в регулярную.
Таким образом, используя такой мощный инструмент, как Wolfram Mathematica, мы можем без особых усилий и знаний о программирование, а главное интуитивно так, как это предлагают классические учебники, наблюдать интересные и загадочные процессы и явления. Главное, что мы можем самостоятельно крутить и вертеть любые параметры системы, что очень важно для понимания. Данный проект являлся моей курсовой работой, я над ним неплохо посидел пару месяцев, но результатом остался доволен. Долгое время крутил анимацию движения своего волчка и игрался с параметрами наблюдая различные траектории движения, чего не было у Лагранжа или Ковалевской.
upd. По просьбам трудящихся залил проект на DropBox
Использовалась Wolfram Mathematica 9.0
Немного о сферическом движении
Сферическое движение — движение ТТ, имеющего одну неподвижную точку. Каждая из точек ТТ при таком движении перемещается по поверхности сферы с центром в точке закрепления. В таком случае говорят о вращательном движении, которое слагается из серии элементарных поворотов вокруг мгновенных осей вращения, проходящих через точку закрепления. Мгновенная ось вращения непрерывно изменяет своё положение, как по отношению к системе отсчёта, в которой рассматривается движение, так и в самом теле, образуя при этом две канонические поверхности, называемые соответственно неподвижным и подвижным аксоидами.
ТТ с неподвижной точкой имеет 3 степени свободы, и его положение по отношению к данной системе отсчёта определяется тремя параметрами, а точнее углами Эйлера. Эти углы определяют три поворота системы, которые позволяют привести любое положение системы к текущему.
Углы Эйлера

Если взять элементарные повороты СК вокруг осей Z и X в порядке Z, X', Z'' на соответствующие углы Ψ, θ и φ, то такое преобразование приводит к выражению матрицы поворота через углы Эйлера. С помощью такой матрицы, происходит поворот ТТ в пространстве.

Применяемые углы имеют следующий физический смысл:
- Угол Ψ — угол прецессии
- Угол θ — угол нутации
- Угол φ — угол собственного вращения
Сферическое движение ТТ, впервые описанное Леонардом Эйлером (нем. Leonhard Euler) имеет решение только в трёх случаях:
- Случай Эйлера — центр масс ТТ, находится в закреплённой точке. Момент внешних сил равен нулю.
- Случай Лагранжа — ТТ является динамически симметричным
 . Центр масс ТТ находится на оси симметрии.
. Центр масс ТТ находится на оси симметрии. - Случай Ковалевской — тело является динамически симметричным, моменты инерции связаны соотношением
 . Центр масс ТТ находится в экваториальной плоскости.
. Центр масс ТТ находится в экваториальной плоскости.
Далее будем говорить о движение тяжелого симметричного волчка в случае Лагранжа.
Уравнения движения в случае Лагранжа
Построим рисунок тяжелого симметричного волчка в поле сил тяжести. Роль волчка отведём конусу.
Рисунок

Уравнения движения получим из теоремы о кинетическом моменте, предварительно записав его в общей форме в подвижной СК.
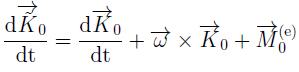
Теперь воспользуемся построенным нами рисунком и записанной теоремой: опуская нудные формулы, учтём моменты инерции симметричного волчка и приводя подобные получаем систему уравнений движения ТТ в поле сил тяжести.

Данная система не решается строго аналитически, а решение представляется только в квадратурах. Мы же решим эту систему численно и проанализируем полученные результаты.
Моделирование случая Лагранжа в системе Wolfram Mathematica
Для начала нам необходимо задать начальные условия нашей системе ДУ:
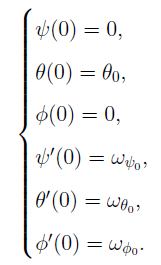
Далее, с помощью возможностей системы компьютерной алгебры, зададим параметры волчка, нарисуем примитивы и решим численно систему ДУ.
Отрывки кода

Затем получим матрицу поворота, о которой мы говорили ранее, встроенными средствами языка, подставим туда численное решение и применим к этому «торту» оператор геометрической трансформации:

Вот в принципе и все сложности решения в пару строк. Осталось только определить графическую область, построить траекторию движения и сделать анимацию, но это уже, как говорится на любителя (можно ограничится и численным выводом матриц преобразования). Оставшаяся часть кода:
Оставшаяся часть

Вывод и анализ результатов в системе Wolfram Mathematica
Вывод результатов программы осуществляется в виде окна с динамическими параметрами начальных условий движения, времени анимации и прозрачностью волчка.
Проанализируем поведение волчка в случае регулярной (вынужденной) прецессии в поле сил тяжести:
Согласно теореме о кинетическом моменте (мы говорили о ней выше), за каждый малый промежуток времени dt вектор момента импульса получает под действием силы тяжести приращение
 , направленное вдоль
, направленное вдоль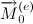 , т.е. лежащее в горизонтальной плоскости перпендикулярно оси волчка. Отсюда следует, что вектор момента импульса и вместе с ним ось волчка равномерно поворачиваются (совершают прецессию) вокруг вертикали, проходящей через точку опоры. Наклоненный к вертикали волчок прецессирует, т.е. помимо вращения вокруг собственной оси поворачивается еще и вокруг вертикальной оси. При быстром собственном вращении эта прецессия (поворот вокруг вертикальной оси) происходит настолько медленно, что с хорошей точностью можно пренебречь той составляющей момента импульса, которая обусловлена прецессией вокруг вертикали. Такое поведение оси волчка называют регулярной прецессией. Это вынужденная прецессия, так как она происходит под действием момента силы тяжести. Все точки волчка, лежащие на его оси, равномерно движутся по круговым траекториям, центры которых лежат на вертикали, проходящей через точку опоры волчка. На рисунке приведена иллюстрация регулярной прецессии волчка.
, т.е. лежащее в горизонтальной плоскости перпендикулярно оси волчка. Отсюда следует, что вектор момента импульса и вместе с ним ось волчка равномерно поворачиваются (совершают прецессию) вокруг вертикали, проходящей через точку опоры. Наклоненный к вертикали волчок прецессирует, т.е. помимо вращения вокруг собственной оси поворачивается еще и вокруг вертикальной оси. При быстром собственном вращении эта прецессия (поворот вокруг вертикальной оси) происходит настолько медленно, что с хорошей точностью можно пренебречь той составляющей момента импульса, которая обусловлена прецессией вокруг вертикали. Такое поведение оси волчка называют регулярной прецессией. Это вынужденная прецессия, так как она происходит под действием момента силы тяжести. Все точки волчка, лежащие на его оси, равномерно движутся по круговым траекториям, центры которых лежат на вертикали, проходящей через точку опоры волчка. На рисунке приведена иллюстрация регулярной прецессии волчка.Регулярная прецессия

Данное событие происходит только при строго определенных начальных условиях.
Теперь можно перейти к исследованию вопроса о том, как будет вести себя вращающийся волчок под действием силы тяжести при начальных условиях, не обеспечивающих немедленного возникновения регулярной прецессии. В общем случае движение волчка должно представлять собой суперпозицию вынужденной регулярной прецессии и нутации, что отображено на рисунке.
Общий случай движения

В первый момент, как только мы отпускаем ось волчка, под действием силы тяжести она действительно начинает падать вниз, что вполне согласуется с нашими интуитивными представлениями. Но по мере того, как ось набирает скорость, траектория ее верхнего конца все сильнее отклоняется от вертикали. Вскоре движение оси становится горизонтальным, как и при регулярной прецессии, но скорость этого движения больше той, что нужна для регулярной прецессии. Траектория конца оси начинает отклоняться вверх. Поднявшись до исходной высоты, ось «замирает» – ее скорость обращается в нуль. Затем все повторяется сначала. Но теперь мы понимаем, что такое своеобразное поведение, когда конец оси движется по циклоидальной траектории, объясняется сложением двух движений – нутации волчка вокруг вектора момента импульса с одновременной вынужденной прецессией этого вектора вокруг вертикали.
Когда нутации малы, вынужденную прецессию называют псевдорегулярной, на рисунке можем наблюдать данное явление. Для быстро вращающихся гироскопов(т.е. очень быстро вращающихся волчков), применяемых в технике, псевдорегулярная прецессия практически не отличается от регулярной. В таких случаях нутация проявляет себя как едва заметное мелкое и частое дрожание оси гироскопа. Кроме того, мелкомасштабные нутации быстро затухают под действием сил трения, и псевдорегулярная прецессия переходит в регулярную.
Псевдорегулярная прецессия

Заключение
Таким образом, используя такой мощный инструмент, как Wolfram Mathematica, мы можем без особых усилий и знаний о программирование, а главное интуитивно так, как это предлагают классические учебники, наблюдать интересные и загадочные процессы и явления. Главное, что мы можем самостоятельно крутить и вертеть любые параметры системы, что очень важно для понимания. Данный проект являлся моей курсовой работой, я над ним неплохо посидел пару месяцев, но результатом остался доволен. Долгое время крутил анимацию движения своего волчка и игрался с параметрами наблюдая различные траектории движения, чего не было у Лагранжа или Ковалевской.
Литература
- Виттенбург, Й. Динамика систем твёрдых тел/ Й. Виттенбург.- Москва: МИР, 1980.-294 с.:
- Вращательное движение.
- Углы Эйлера.
- Вынужденная прецессия гироскопа.
upd. По просьбам трудящихся залил проект на DropBox
Использовалась Wolfram Mathematica 9.0