Оригинал: Raúl Rojas — «Konrad Zuse’s Legacy: The Architecture of the Z1 and Z3», IEEE Annals of the History of Computing, Vol. 19, No. 2, 1997
Эта статья представляет детальное описание архитектуры вычислительных машин Z1 и Z3, разрабатываемых Конрадом Цузе в Берлине с 1936 по 1941 гг. Информация была в основном получена из детального изучения патента, поданного Цузе в 1941 г. Более глубокая оценка была получена из программной симуляции машинной логики. Z1 была основана исключительно на механических компонентах, а в Z3 использовались электромеханические реле, но обе машины имели общую логическую структуру и программную модель. Z1 и Z3 обладали такими свойствами современных вычислительных машин как: разделение памяти и процессора, способность оперировать числами с плавающей запятой, вычислять 4 основные арифметические операции и квадратный корень. Программы хранились на перфоленте и считывались последовательно. В последующей статье я рассмотрю архитектуру Z1 и Z3 в исторической перспективе, и произведу сравнение с компьютерами построенными в других странах.
Конрад Цузе признается в Германии как отец компьютера, и его Z1, программируемый автомат, строящийся с 1936 по 1938 гг., считается первым компьютером в мире. В других странах это значение придается другим ученым, и там проходят долгие и острые споры по вопросу, кто является истинным изобретателем компьютера. Иногда споры переходили в глубокие и детальное описание технологических особенностей конкретных машин. К примеру ENIAC ( Electronic Numerical Integrator and Computer ) считается «Первой широкомасштабной, полностью электронной вычислительной машиной в мире». ENIAC строился в Школе Электротехники Мура при Пенсильванском университете (Moore School of Electrical Engineering of the University of Pennsylvania ) с 1943 по 1945 гг. Он решил первую задачу в декабре 1945 и был представлен в феврале 1946. Другим кандидатом на титул первого компьютера считается Mark I, строящийся Говардом Айкеном в Гарвардском университете с 1939 по 1944 гг. Mark I был электромеханической машиной, т.е. построенной не на чисто механических элементах, как в более ранних вычислительных устройствах, и не на электронике, уже доступной в то время. В машине Джона Атанасова (позже названной ABC) из Государственного Колледжа штата Айова, строящейся с 1939 по 1944, использовались вакуумные трубки, но при этом машина имела ограничения на сложение и вычитание векторов, и имеющаяся структура не подходила для универсальных вычислений. Z1 является прямой противоположностью этих машин, более гибкая, построенная для исполнения длинных и модифицируемых последовательностей инструкций, считываемых с перфоленты. Машины Z3 и Z4 не были электронными и обладали меньшими габаритами. Z3 была построена и успешно прошла испытания раньше чем Mark I, и поэтому была названа первой программируемой вычислительной машиной в мире. Конечно давние дискуссии не будут завершены на этой статье, но я хочу показать, насколько передовыми были машины Цузе, с точки зрения современной компьютерной архитектуры и по сравнению с архитектурой того времени.
Цузе, будучи студентом Берлинского политехнического, начал работать над вычислительной машиной в 1930х. Он понял, что может построить автомат способный выполнять последовательность математических операций, которые требуются для построения математических таблиц. Придя из гражданской инженерии, он имел опыт в области электроники, но не был знаком с технологиями, используемыми в обычных механических калькуляторах. Однако эта нехватка знаний дала ему преимущество, т.к. он смог переосмыслить все вопросы машинной арифметики и найти новые оригинальные решения.
Цузе решил построить свою первую экспериментальную вычислительную машину основываясь на двух главных идеях:
Годом ранее Джон фон-Нейманн объяснял преимущество компьютерной архитектуры с процессором, разделяющим память. Цузе пришел к такому же выводу. Надо заметить, что Чарльз Бэббидж пришел к тем же выводам проектируя свою Аналитическую машину в прошлом столетии. В 1936 г. Цузе закончил работу над памятью для своей машины, и назвал ее Speicherwerk (нем. — Запоминающие устройство) — термин Speicher использовался в Германии вместо антропоморфного термина Memory (англ. — Память), который ввел фон-Нейманн, Бэббидж же использовал термин Store (англ. — Хранилище). Память являлась механическим устройством, но не обычного типа. Вместо использования шестеренок (их использовал Бэббидж в прошлом веке), Цузе реализовал логические и арифметические операции на скользящих металлических рейках. Рейки могли перемещаться в одном из двух направлений (прямое и обратное) и следовательно являлись двоичным механизмом. Процессор Z1 был построен спустя 5 месяцев после построения памяти. При работе с памятью он был крайне ненадежным. Главная проблема была в точности синхронизации, которая требуется для предотвращения чрезмерной механической нагрузки на подвижные части. Интересно отметить, что в том же году, когда Цузе закончил работать над памятью, Алан Тьюринг написал свою новаторскую работу On computable numbers (англ. — О вычислимых числах), в которой формализовал интуитивно понятные вычисления.
Машина Z1, несмотря на ненадежность, показала, что Архитектурный дизайн был целесообразным и побудила Цузе изучить другие виды технологий. Следуя совету своего друга Хельмута Шряера, он рассмотрел электромеханические реле. Цузе построил «промежуточную» модель ( Z2 ) на смешанной технологии (процессор строился на реле, а память осталась механической). В 1938 г. Цузе начал разработку Z3, машину полностью построенную на реле, но с логической структурой от Z1. Она была готова к эксплуатации в 1941 г., за 4 года до ENIAC.
Эта работа предполагает детальное рассмотрение архитектуры машин Z1 и Z3. Цузе реконструировал свою машину Z1 в Берлине в 80х годах, и сейчас она выставляется в Берлинском музее транспорта и технологий. Однако доступная информация описывает устройство механической памяти[12]. Цузе документировал Z3 в патентном приложении Z-391 1941г, но его анализ затруднен из-за нестандартной нотации и терминологии[14]. Книга [4] о Z3 является хорошим источником для понимания исторической обстановки, окружающей исследования Цузе, но не описывает Z3 в деталях. Т.к. Z1 и Z3 эквивалентны с логической и функциональной точки зрения, в дальнейшем, я буду ссылаться только на Z3. Основным архитектурным отличием является то, что Z1 нет поддержки операции извлечения квадратного корня. Остальные минимальные отличия сводятся к различаю в количестве бит в арифметических операторах процессора (Z1 использует меньшую разрядность мантиссы в числах с плавающей запятой) и в количестве циклов необходимых для каждой инструкции. С минимальной оговоркой, принимая во внимание только архитектуру, можно считать Z1 и Z3 эквивалентными машинами. Проводились споры, действительно ли реконструированная Z1 соответствует оригинальной Z1, уничтоженной во время второй мировой войны. Цузе реконструировал машину Z1 основываясь исключительно на свои воспоминания, и вполне возможно, что реконструированная машина имеет больше общего с Z3, чем с оригинальной Z1. Так же, Цузе указывает в своих мемуарах на базовое сходство Z1 и Z3 [15], и подтверждает этот аспект своей работы в частном интервью.
В этом разделе большинство архитектурных особенностей приведены для Z3. Вначале я представлю обзор архитектуры, потом перейду к деталям.
Z3 работала с числами с плавающей запятой, в отличие от других ранних вычислительных автоматов, таких как Mark I, ABC или ENIAC, работающих с числами с фиксированной запятой. Цузе разработал то, что позже назвал «полулогарифмическая запись», которая соответствует современному представлению чисел с плавающей запятой.
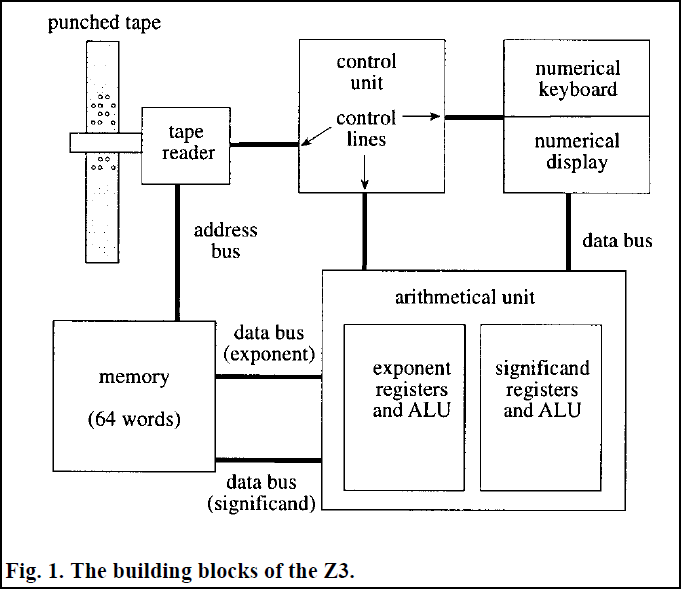
На рис. 1 изображены основные составные блоки Z3. Первой особенностью архитектуры является разделение процессора и памяти. Z3 включает двоичную память (способной хранить 64 числа с плавающей запятой), двоичный процессор для чисел с плавающей запятой, устройство управления и устройства ввода/вывода. Память и Арифметический блок соединены шиной данных, передающей экспоненту и мантиссу числа с плавающей запятой. Устройство управления содержит микропрограммы для каждой инструкции. Управляющие сигналы поступают в процессор, память и устройство ввода/вывода для осуществления синхронизации всех блоков. Устройство чтения перфоленты предоставляет код операции для каждой инструкции, а так же адрес для доступа к памяти. Устройство ввода/вывода подключено к процессору шиной данных.
На рис. 2 изображено представление используемое в Z3. Первый разряд используется для хранения знака, следующие 7 разрядов хранят экспоненту, а последние 14 разрядов хранят мантиссу. Разряды экспоненты называются Часть А и обозначаются как a6,...,a0. Разряды мантиссы называются Часть B и обозначаются как b0,b-1,...,b-14. Экспонента закодирована в дополнительном коде и может содержать значения в диапазоне от -64 до 64. Мантисса хранится в нормализованной форме, в которой первый разряд после запятой (b0) всегда должен быть установлен единицу [5]. Этот разряд не хранится в памяти (поэтому он не показан на рис. 2), так что эффективный диапазон значений мантиссы в памяти равен 15 битам. Однако возникает проблема с числом 0, т.к. нормализованная мантисса не может его выразить. В Z3 существует соглашение, согласно которому, любая мантисса с экспонентой -64 рассматривается как 0. Любое число с экспонентой равной 63 считается бесконечно большим. Операции над 0 или бесконечно большим вызывают исключения, и специальные аппаратные контроллеры устанавливают в процессоре флаги исключения (рассмотрим ниже).
Учитывая это соглашение, минимальным числом в памяти Z3 является 2-63 = 1.08x10-19, а максимальным 1.999x262 = 9.2x1018. Аргументы для расчета могут вводиться в виде десятичных чисел с клавиатуры (четырехзначные). Экспонента десятичного представления вводится нажатием соответствующей кнопки в ряду кнопок помеченных -8,-7,...,7,8. Оригинальная Z3 позволяла вводить только числа в диапазоне от 1x10-8 до 9,999x108. Реконструированная Z3 из Германского музея в Мюнхене имеет дополнительные кнопки для больших экспонент. С этим улучшением стало возможно вводить полный числовой диапазон машины с клавиатуры. Немного скажем о выводе. Z3 не печатала результаты программных процедур. Единственное число отображалось на массиве ламп, представляющих числа от 0 до 9. Максимальным числом, который Z3 была способна отобразить являлось 19,999, а минимальным 00001. Максимальной отображаемой экспонентой было +8, а минимальной -8.

Программа Z3 хранится на перфоленте. Одна инструкция использует 8 разрядов из каждого ряда на ленте. Набор инструкций Z3 состоит из 9 инструкций представленных в таблице 1. Они поделены на 3 группы: ввод/вывод, память и арифметические операторы. Код операции имеет переменную длину от 2х до 4х разрядов. Операторы памяти кодируют адрес слова в младших 6 разрядах, которые способны адресовать 64 слова, как упоминалось ранее.
Инструкции на перфоленте могут располагаться в любом порядке. Инструкции Lu и Ld (Чтение с клавиатуры и Отображение на дисплей) останавливают машину, чтобы у оператора было достаточно времени для ввода числа и записи результата.
Z3 не имеет инструкций условных переходов. Циклы реализуются простым скреплением двух концов перфоленты, но это не позволяет реализовывать условные последовательности инструкций. Следовательно Z3 не является универсальным компьютером в описании Тьюринга.
Таблица 1. Множество инструкций и их кодов машины Z3
Z3 является синхронной машиной. Каждый цикл разделен на 5 стадий, называемых I, II, III, IV и V. На стадии I происходит декодирование инструкции с перфоленты. Основными арифметическими операциями являются сложение и вычитание экспоненты и мантиссы. Операции могут исполняться в первых трех стадиях каждого цикла. Стадии IV и V используются для подготовки аргументов к следующим операциям или вывода результата.
Таблица 2. Число циклов, необходимых для выполнения инструкций
По словам Цузе, умножение выполняется за 3 секунды. Учитывая то, что операция умножения требует 16 циклов, можно оценить, что рабочая частота Z3 составляет 3/16 = 5,33 Гц. Любопытно то совпадение, что симулятор Z3, который мои студенты реализовали на персональном компьютере, тоже требует около 3х секунд для умножения.
Число циклов необходимых для инструкций Ввода с клавиатуры и Вывода на дисплей переменно, потому что зависит от экспоненты аргументов. Т.к. ввод должен преобразовывать десятичное представление в двоичное, количество умножений на 10 или 0,1 определяется значением десятичной экспоненты (рассмотрим ниже).
Сложение и вычитание требуют больше одного цикла потому, что в случае с числами плавающей запятой, нам необходимо привести экспоненты обоих аргументов к одному значению. Это требует дополнительных сравнений и сдвигов.
Число может быть записано в память за 0 циклов в том случае, когда результат последней арифметической операции может быть перенаправлен на требуемый адрес памяти. В этом случае цикл, необходимый для инструкции записи, совпадает с последним циклом арифметической операции.
Очень важно описать машину Z3 с точки зрения программиста. С точки зрения программного обеспечения, Z3 состоит из 64 слов в памяти, способных загружаться в 2 регистра с плавающей запятой, которые я для простоты назову R1 и R2. Два регистра хранят аргументы для арифметической операции. Программист может писать любые последовательности инструкций, но должен помнить о состоянии регистров.
Важно помнить последовательность: Первая операция загрузки в программе (Pr z) загружает содержимое адреса z в R1. Все последующие операции загрузки загружают слово из памяти в R2. Инструкция Ввода с клавиатуры загружает число в R1 и ОЧИЩАЕТ R2, который используется как временное значение при преобразовании десятичного ввода в двоичное представление.
Арифметические операции не содержать аргументов в коде операции. Всегда используются следующие аргументы:
R2 сбрасывается в 0 после арифметический инструкций, записывающих результат в R1. Последующие операции загрузки из памяти отсылают значение в R2. Инструкции записи в память и вывода на дисплей всегда берут значение из R1, который содержит результат последней арифметической операции. После операций сохранения или вывода, R1 сбрасывается в 0 (при отключении реле, которые потом будут готовы к принятию нового значения). Следующая загрузка из памяти происходит в R1.
Приведем пример для лучшего понимания программной модели Z3. Предположим, нам требуется рассчитать полином методом Горнера.
x ( a2 + x ( a3 + x a 4)) + x5
Далее будем считать, что аргументы a4, a3, a2 и a1 хранятся в четвертой, третей, второй и первой ячейках памяти соответственно. Значение z хранится в пятой. Программа приведена ниже:
После исполнения последней инструкции процессор сбрасывается с исходное
состояние.
В это разделе, я рассмотрю структуру Z3 и опишу основные составные блоки в
деталях. Важно показать, как осуществляется синхронизация между
компонентами.
На рис. 3 изображена упрощенная схема арифметического устройства. Он состоит из двух частей: левая осуществляет операции над экспонентой числа с плавающей запятой, а правая — операции над мантиссой. Регистры Af и Bf хранят экспоненту и мантиссу того, что с программной точки зрения называется R1. Я буду представлять R1, как пару регистров < Af, Bf>. Пара регистров < Ab, Bb> хранит экспоненту и мантиссу R2. Пара < Aa,Ba> хранит экспоненту и мантиссу третьего временного регистра с плавающей запятой, невидимого для программиста. Два Арифметико-логических устройства (АЛУ) A и B используются для сложения и вычитания экспонент и мантисс, соответственно. Экспонента и мантисса результата помещаются в Ae и Be соответственно. Пара < Ae, Be> рассматривается как внутренний регистр, недоступный для программиста. В части B, мультиплексор позволяет выбрать результат операции между Ba и выходом АЛУ. Мультиплексор управляется с помощью переключателя Bt (если Bt=0, то Be получает значение Ba).

Маленькие блоки обозначенные Ea, Eb, Ec, Ed, Ef, Fa, Fb, Fc, Fd и Ff являются релейными блоками (далее РБ), открывающими и закрывающими шины. К примеру, чтобы предать значение содержимое регистра Af в регистр Aa, необходимо установить РБ Ea в единицу. Как мы можем видеть из рис. 3, содержимое Af может быть перенесено в Aa или Ab, а содержимое Ae может быть перенесено в Aa, Ab или Af, в зависимости от состояния РБ. Часть B арифметического устройства устроена аналогично, но с добавлением мультиплексора управляемого переключателем Bt и сдвигающих устройств между Bа и Ba, и между Bf и Bb. Первое сдвигающее устройство может сдвигать мантиссу в пределах 2 разрядов влево или 1 разряда вправо. Оно осуществляет деление Bf на 4 или умножение на 2. Второе сдвигающее устройство способно сдвинуть Af на одну из 16 позиций влево или одну из 15 позиций вправо. Эти сдвигающие устройство требуется для сложения и вычитания чисел с плавающей запятой. Операции умножения и деления на степени двойки могут осуществляться с последующей арифметической операцией без затрат дополнительного времени.
Таблица 3. Разрядность регистров
Как мы можем видеть из списка, Ae имеет дополнительные разряд для сохранения результата сложения экспонент аргументов. Часть B имеет 2 дополнительных разряда (b-15 и b-16) и явный разряд b0, не хранящийся в памяти. -15 и -16 разряды введены для увеличения точности вычислений. Следовательно, общая разрядность, необходимая для хранения результата арифметических операций в Bf, составляет 17 бит. Регистрам Ba и Bb требуется дополнительные разряды (ba2, ba1 и bb1) для хранения промежуточных результатов некоторых вычислений. Например, для алгоритма расчета квадратного корня может потребоваться 3 разряда слева от десятичной запятой.
Простейшей операцией над каналом данных является сложение и вычитание мантиссы и экспоненты. Когда переключатели As или Bs установлены в 1, АЛУ переводит второй аргумент в дополнительный код, т.е. меняет его знак (Ab или Bb). Следовательно, если переключатель As установлен в 1, то АЛУ части A осуществляет вычитание, в противном случае сложение. Часть B и переключатель Bs работают аналогично.
Предположим имеется два числа с равными экспонентами, которые необходимо сложить. Первая экспонента хранится в Af, а вторая в Ab. Поскольку они равны, эта часть машины не должна производить никаких операций. В части B, мантисса первого числа хранится в Bf, а мантисса второго в Bb. Первый этап состоит в переносе числа из Bf в Bf, для чего необходимо установить релейный блок Fa в 1. Далее происходит сложение. Для того чтобы результат Ba+Bb записался в Be, необходимо установить переключатель Bt в 1. РБ Ff в настоящий момент установлен в 1, и результат помещается в Bf. Архитектура должна предоставлять правильную последовательность воздействий на переключатели для исполнения желаемой операции. Z3 осуществляет это благодаря технике, очень похожей на микропрограммирование.
На рис. 4 изображена детальная схема устройства управления и панелей ввода/вывода. Схема Pa декодирует код операции, считаный с перфоленты. Если это инструкция памяти, то схема Pb посылает на шину адреса младшие 6 бит из кода операции. Устройство управления определяет микропоследовательности инструкций. Для каждого оператора из набора инструкций имеется специальные схемы.
Схема Z представляет клавиатуру, используемую для ввода десятичных чисел. Только одна кнопка в каждом из четырех столбцов может быть нажата. Экспонента устанавливается нажатием одной из кнопок, помеченных от -8 до 8, на схеме K. Дисплей очень похож на панель ввода, его лампы высвечивают принятое десятичное число, и его экспоненту (схема Q). Обратите внимание, что на дисплее выводится пятая цифра (может принимать значения только 0 или 1).
После ввода десятичного числа, оно передается по шине данных в регистр Ba, и начинает выполнятся специальная последовательность операций. Десятичное число, введенное с клавиатуры, должно быть преобразовано в двоичное представления. Для этого требуется произвести несколько умножений, количество которых определяется значением экспоненты. Для экспоненты равной нулю, на полное преобразование затрачивается 9 циклов, а для экспоненты равной -8, затрачивается 9+4*8 = 41 цикл.

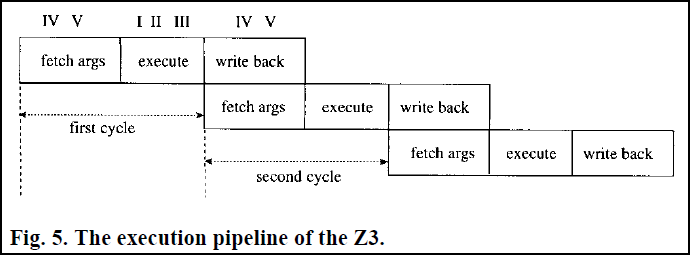
В основе Устройства управления лежит контроллер микропоследовательностей. Перед рассмотрением принципа его работы, нам необходимо подробно рассмотреть алгоритмы арифметических инструкций Z3. На рис. 5 показана основная идея. Каждый цикл состоит из 5 стадий. На стадиях IV и V осуществляется ввод информации в машину. На стадиях I, II и III происходит сложение/вычитание, в частях A и B. Я назвал эту фазу инструкции — «исполнение». Типичная инструкция осуществляет выборку аргументов, исполнение и запись результата. Цузе удалось сократить время исполнения за счет перекрытия стадий выборки аргументов для следующей инструкции и записи результата текущей. В итоге можно считать, что исполнительный цикл состоит из двух этапов (на рис. 5 обозначены первые два цикла).
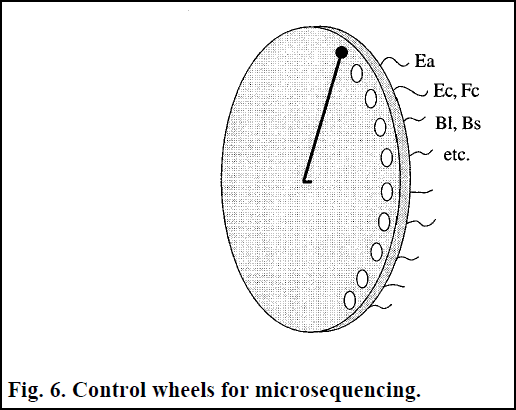
Контроллер микропоследовательностей реализован с помощью специального управляющего колеса. Реализованы отдельные колеса для алгоритма умножения, деления и взятия квадратного корня. Подвижный рычаг, изображенный на рис. 6, начинает вращаться по часовой стрелке, как только устройство управления декодирует соответствующую инструкцию. За каждый цикл рычаг перемещается на одну позицию. Рычаг проводит электричество и активирует схемы с которыми приходит в контакт. В примере изображенным на рис. 6, подвижный рычаг устанавливает переключатель Ea в 1 на первом цикле. Это ведет к переносу числа из регистра Af в Aa. На следующем цикле, активизируются переключатели Ec и Fc. В этом случае результаты операции в частях A и B записываются в регистры Aa и Ba, соответственно. Как мы можем видеть, использование таких колес управления предоставляет платформу для легкой модификации микропоследовательностей определенных операторов. Аналогично устроены контроллеры микропоследовательностей в современных микропроцессорах. Я не назвал этот способ микропрограммированием, потому что в нашем случае контроллер микропоследовательностей является аппаратным, но очевидно, что микропоследовательности и микропрограммы тесно связаны.
Использование контроллеров микропоследовательностей позволило Цузе сильно упростить машину. После того, как основные схемы были готовы на их основе совершенствовалось устройство управления, пока не удалось достичь оптимальной последовательности микрокоманд. Инженер, проектируя «микропрограмму», должен учитывать множество деталей, иначе короткое замыкание может уничтожить машину. Механическая Z1 была более чувствительна в этом отношении, чем Z3. По завершению этого этапа был список последовательностей, которые программист должен избегать, что бы не допустить порчу оборудования. Одна из таких последовательностей по неосторожности была запущена в Берлинском музее технологий и транспорта, и привела к небольшим повреждениям реконструкции Z1 в 1994 г.
Важной особенностью сумматора Z3, является вычисление суммы и разности методом, называемом схемой ускоренного переноса. Если бинарное сложение осуществляется прямым образом, перенос передается от каждого разряда на один бит далее. В случае с мантиссой, требуется 16 циклов для передачи переноса одного разряда. Сложение в реализации Цузе значительно быстрее, где сложение и вычитание осуществляется в течении I, II и III фазах одного цикла. Для вычитания второй аргумент переводится в обратный код с добавлением единицы к младшему разряду (дополнительный код).
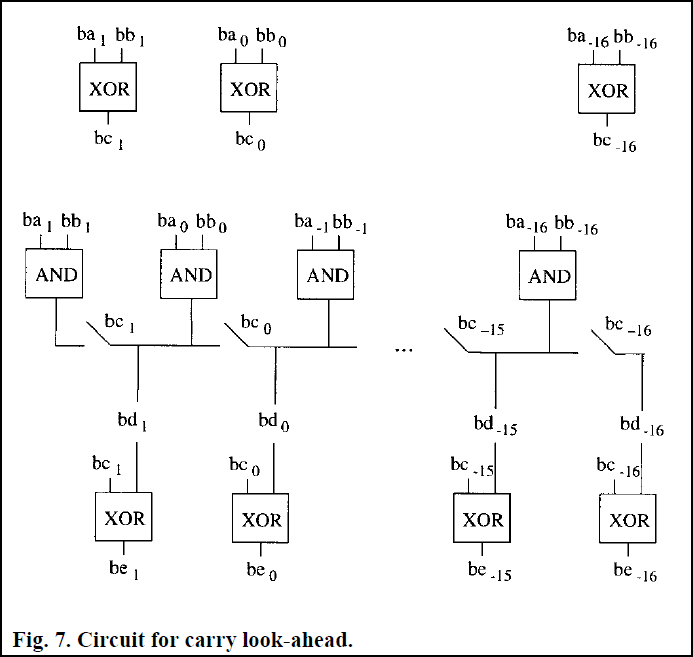
Рассмотрим сложение регистров Ba и Bb. Я буду обозначать i-ый разряд регистра Bb как bbi или Bb[i]. В такой нотации будут обозначаться все регистры. Первый промежуточный результат получается поразрядным Исключающим ИЛИ между двумя регистров, т.е. bci=bai XOR bbi. Второй промежуточный результат получается поразрядной конъюнкцией между двумя регистрами, т.е. bai AND bbi. Следующая операция находит разряды, для которых требуется перенос. Промежуточный результат bdi вычисляется по схеме, изображенной на рис. 7. Обратите внимание, что если разряд установлен в единицу, то по соответствующей линии переноса идет ток, в противном случае источник питания отключен (что бы не произошло короткое замыкание). Схема подключения переключателей bc1,...,bc-16 показана на рис. 7. Если разряд bci установлен в единицу, соответствующий переключатель разомкнут. Итоговый результат равен bei = bdi XOR bci. Подобная схема позволяет переместить перенос на последний разряд значительно быстрее. В случае, если все переключатели активны, перенос перемещается от первого разряда к последнему не затрачивая времени.
В этом разделе я опишу алгоритмы над числами с плавающей запятой, используемые в Z3. Все они, без исключения, используются в обычных маленьких последовательных процессорах с плавающей запятой.
Основной проблемой записи с плавающей запятой является соглашение, касательно представления числа 0. Z3 решает эту проблему с помощью исключений (переполнение и потеря разрядов) для отслеживания значения экспоненты после арифметических операций или операции загрузки из память. Специальные схемы следят за состоянием шины Ae и перехватывают исключения. Любое число с экспонентой -64 является 0: Переключатель обозначаемый Nn1 устанавливается в 1, если такое число хранится в паре регистров < Af,Bf>. Если такое число хранится в паре регистров < Ab,Bb>, переключатель Nn2 устанавливается в 1. Поэтому, мы всегда знаем, является-ли один из аргументов арифметической операции нулем. Нечто подобное происходит для любого числа с экспонентой 63 (бесконечно большое). В это случае, переключатели Ni1 или Ni2 сбрасываются в 0, если соответствующие пары регистров хранят такие числа.
Операции включающие «исключительные» числа (нуль и бесконечность) производятся как обычно, но с помощью специальной схемы результат подменяется. Рассмотрим, к примеру, умножение с первым аргументом равным нулю (Nn1 установлен в 1). Вычисление проходит как обычно, но в каждом цикле специальная схема выдает результат -64 из сумматора Части A. Совершенно не важно, какие операции проводились с мантиссой, поскольку экспонента равна -64, а значит и конечный результат равен нулю. Деление на нуль происходит аналогично. Z3 может обнаружить неопределенности, такие как 0/0, ∞-∞, ∞/∞ и 0*∞. Во всех этих случаях загорается индикатор соответствующего исключения на панели вывода и машина останавливается. Z3 всегда вычисляет правильный результат, когда один из аргументов является нулем или бесконечностью, а второй конечным ненулевым числом. Но это не относится к Z1. Цузе думал об обработке исключений в Z1, но она так и осталась не реализованной. Машина выдает неверный результат в некоторых вычислениях с нулем.
Дополнительная схема смотрит на экспоненту результата, на выходе из сумматора Части А. Если экспонента больше или равна 63, то произошло переполнение и результат должен быть установлен в бесконечность. Если экспонента упала до -64, то произошла потеря разрядов и результат должен быть установлен в нуль. Для этого соответствующие переключатели (Nn1 или Ni2) устанавливаются в 1.
Цузе реализовал обработку исключений используя всего 5 реле. Эта особенность Z3 является одной из самых элегантных во всем дизайне. Большинство ранних микропроцессоров в 1970х не обладали обработкой исключений и реализовывали их программно. Подход Цузе более совершенный, поскольку он освобождает программистов от необходимости все время проверять границы чисел перед каждой операцией.
Для сложения или вычитания двух чисел с плавающей запятой x и y, они должны быть представлены с одинаковой экспонентой. После этого сложение и вычитание осуществляется только над мантиссой. Если экспоненты отличаются, мантисса меньшего числа сдвигается вправо на необходимое количество разрядов ( а экспонента соответственно инкремируется так, чтобы операнд сохранял свое значение ), чтобы экспоненты сравнялись. Конечно может случиться так, что меньшее число станет нулем после 17 смещений вправо.
Знаки операндов сравниваются перед принятием решения о типе выполняемой операции. Если запрошено сложение, то выполняется сложение в случае одинаковых знаков и вычитание в случае различных знаков. Если запрошено вычитание и знаки одинаковы, то выполняется вычитание, а если различны то выполняется сложение.
Специальная схема устанавливает знак результата исходя из знаков операндов и знака промежуточного результата.
Сложение и вычитание управляется цепью переключателей (а не Колесом управления микропоследовательностями), т.к. пока максимальное число необходимых этапов не велико. В таблице 4 приведены сигналы, необходимые для сложение двух чисел. Изначально аргументы операции сложения хранятся в парах регистров < Af, Bf> и < Ab,Bb>. На первом цикле экспоненты сравниваются. На втором цикле мантисса числа с большей экспонентой загружается в регистр Ba, а мантисса числа с меньшей экспонентой загружается в регистр Bb. Мантисса в регистре Bb сдвигается вправо на число равное абсолютному значению разности экспонент (система обработки исключений заботится о случае, когда меньшее число становится нулем после сдвига). На стадиях I, II и III второго цикла, мантиссы складываются и в конце процессор проверят, является ли результат большим двух. Если является, мантисса сдвигается на одну позицию вправо, а экспонента инкремируется. Важно заметить, что проверка «if(Be > 0)» осуществляется в Части А арифметического блока после того, как Be будет вычислена в Части B на стадиях I, II и III цикла 2.
Таблица 4. Циклы алгоритма сложения
В случае вычитания требуется 4 или 5 циклов. В таблице 5 представлены сигналы, необходимые для операции вычитания. Первые два цикла полностью идентичны первым двум циклам алгоритма сложения, за исключением того, что мантиссы вычитаются. Цикл 3 выполняется только в случае если мантисса результата положительная. Цикл 4 очень важен: разность нормализованных мантисс может иметь много нулей в первых разрядах слева. Результат нормализуется путем сдвига Be влево на необходимое число разрядов (это осуществляется сдвигающим устройством между переключателем Fd и регистром Bb). Число сдвигов вычитается из экспоненты в Части А процессора. В цикле 5 результат записывается в пару регистров <Af, Bf>.
Таблица 5. Циклы алгоритма вычитания
Алгоритм умножения Z3 похож на один из методов десятичного умножения на пальцах. Метод основан на повторяющихся сложениях множителя с отдельными цифрами множимого. В начале работы алгоритма первый операнд хранится в паре регистров < Af,Bf>, а второй операнд в паре регистров < Ab,Bb>. Промежуточная пара регистров < Aa,Ba> сброшена в 0. В таблице 6 приведена микропоследовательность, выполняемая Колесом управления микропоследовательностями для осуществления умножения. Алгоритм требует 16 циклов. В умножении участвуют только разряды с -14 по 0. Экспоненты складываются на первом цикле, а результат сложение циклически хранится в Части А Арифметического блока. Мантиссы обрабатываются в Части B. Регистр Ba хранит промежуточный результат вычислений.
Основной цикл умножения имеет следующий вид:
Ba := Be / 2
Be := Ba + Bb * (i-ый бит Bf)
Для i = -14,..,0. Промежуточный результат в Be сдвигается на один разряд вправо для выполнения выражения Ba := Be / 2. Эта операция выполняется в сдвигающем устройстве, подключенном к переключателю Fc.
Результатом умножения мантисс является число 1 < = r < 4 (для операндов в заданных пределах). На последнем цикле результат проверяется на выполнения условия r > = 2. Если условие выполняется, то результат сдвигается на один разряд вправо, а экспонента инкремируется.
Таблица 6. Циклы алгоритма умножения
Алгоритм деления очень похож на алгоритм умножения, за тем исключением, что вместо циклического сложения используется циклическое вычитание. В начале работы алгоритма делимое хранится в паре регистров <Af,Bf>, а делитель в паре регистров <Ab,Bb>. Промежуточная пара регистров <Aa,Ba> сброшена в 0. В таблице 7 приведена микропоследовательность выполняемая Колесом управления микропоследовательсностями. Алгоритм требует 18 циклов.
Основная идея алгоритма очень проста. Экспонента результата получается в результате вычитания экспонент делимого и делителя. Теперь о мантиссах: Пусть нам необходимо вычислить x/y для мантисс x и y. Т.к. мы имеем дело с нормализованными числами, то первая цифра результата равна единице, в случае если x >= y, и нулю в случае если x < y. В первом случае мы присваиваем в первую цифру результата 1 и вычисляем остаток, который равен x — y. Остаток рекурсивно делится на y. Для этого он сдвигается на один разряд влево и новый результативный бит сохраняется в регистре Bf на позиции -1 (таким образом компенсируя эффект сдвига). В случае если результативный бит равен нулю, то остаток равен просто x и рекурсивное деление продолжается как и в первом случае.
Основное цикл деления имеет следующий вид:
Ba := 2 × Be
if (Ba–Bb > 0) then Be := Ba–Bb, Bf[i] := 1
else Be := Ba
Bf[i] := 0
Для i = 0,..,-14. Промежуточный результат в Be сдвигается на один разряд влево для выполнения выражения Ba := 2 x Be. Эта операция выполняется в сдвигающем устройстве, подключенном к переключателю Fc.
Результатом деления мантисс является число 1/2 < r < 2. Это условия проверяется в циклах 17 и 18. Если r < 1, то единица вычитается из экспоненты и результат сдвигается на один разряд влево, чтобы получить нормализованное число.
Таблица 7. Циклы алгоритма умножения
Алгоритм извлечения квадратного корня является основной изюминкой Z3. В таблице 8 представлена микропоследовательность, состоящая из 20 циклов, необходимая для вычисления квадратного корня. Изначально аргумент операции хранится в паре регистров <Af,Bf>. Пара регистров <Aa,Ba> сброшена в 0. Алгоритм вычисляет квадратный корень числа с четной экспонентой. Если экспонента числа является не четной, то мантисса сдвигается на 1 разряд влево и экспонента декремируется. Итоговая экспонента (рассчитанная в цикле 19) равна половине исходной экспоненте.
Основная идея этого классического алгоритма заключается в сведении операции извлечения квадратного корня к операции деления. Для извлечения квадратного корня из x, нам потребуется ряд Q, таких что x/Q=Q. Итоговое Q получается последовательно установкой i-го разряда в 1 с последующей проверкой условия x > Q2. Если условие перестало выполняться, то i-ый разряд должен быть сброшен в 0.
Пусть мы уже вычислили результат с нулевого по -i+1 разряд. Обозначим через Q-i+1 мантиссу:
Q-i+1 = Bf[0] * 20 + Bf[-1] * 2-1 +… + Bf[-i+1] * 2-i+1
Далее разряд -i устанавливается в q-i, что должно сохранить условие:
x >= Q-i2 = ( Q-i+1 + q-i * 2-i )2
Это условие истинно, если:
x — Q-i2 = (x — Q-i+12) — 2-i q-i (2 Q-i+1 + 2-i q-i ) >= 0
Определим t-i с помощью выражения:
2-i * t-i = x Q-i2 = (x — Q-i+12) — 2-iq-i(2 Q-i+1 + 2-i q-i)
Это может быть записано как:
2-i t-i = t-i+1 2-i+1 — 2-i q-i ( 2 Q-i+1 + 2-i q-i )
в которой мы используем рекурсивное определение:
2-i+1 t-i+1 = ( x — Q2-i+1 )
Упростив предыдущее выражение мы получаем:
t-i = 2 t-i+1 — q-i (2 Q-i+1 + 2-i q-i)
Если t-i положительный для q-i = 1, то мы устанавливаем разряд -i итогового результата в 1, т.е. Bf[-i] := 1. Если же t-i отрицательный, то мы устанавливаем Bf[-i] := 0. Рекурсивные вычисления начинаются с t0 = x. Q-i+1 на каждом шаге представляет частичный результат, хранящийся в Bf. Разряд -i предварительно устанавливается в 1 и проверяется знак t-i. Основной цикл алгоритма извлечения квадратного корня для разряда -i имеет следующий вид:
Ba := 2 x Be
Bb := 2 x Bf
Bb[-i] := 1
if( Ba — Bb >= 0 ) then Be := Ba — Bb, Bf[-i] := 1
else Be := Ba, Bf[-i] := 0
Для вычисления квадратного корня используются все разряды регистра Bf. Если исходное число находится в заданном диапазоне, то результат тоже находится в заданном диапазоне.
Таблица 8. Циклы алгоритма извлечения квадратного корня
Две наиболее сложные инструкции Z3 c вводом и выводом в десятичной системе счисления. Десятичные числа из 4 цифр вводятся через клавиатуру и конвертируются в бинарное представление. Это осуществляется путем чтения каждой цифры последовательно, преобразования ее в двоичное представление и сохранения в разряды Ba[-10], Ba[-11], Ba[-12] и Ba[-13] регистра Ba. Число в регистре умножается на 10 и процедура повторяется с оставшимися цифрами. После 4 итераций десятичный ввод полностью преобразуется в двоичное представление (экспонента двоичного представления формируется косвенно через сдвиги при умножении на 10). Наиболее сложную часть составляет обработка экспоненты. Если экспонента e положительна, мантисса умножаться e раз на 10. Если отрицательная, то |e| раз на 0.1. Умножение на 10 относительно простое: мантисса в Be может быть сдвинута на 1 разряд влево и потом сохраниться в Ba (т.е. Ba := 2 x Be). В тоже время Be может быть сдвинута на 3 разряда влево и потом сохраниться в Bb (т.е. Bb := 8 x Be). Сложение Ba и Bb дает искомый результат: умножение числа из Be на 10. Процесс занимает 4 цикла для каждого умножения, итого 32 цикла для десятичной экспоненты +8. Так как операции чтения требуется минимум девять циклов, то это означает, что десятичное число с экспонентой +8 читается за 41 циклов.
В случае отрицательной экспоненты, умножение на константу 0.1 осуществляется так же с помощью сдвигов и сложения. Это умножение немного сложнее, т. к. число 0.1 в двоичном представлении периодично. Описание микропоследовательности увело бы нас слишком далеко от основной темы, так что мы ее опустим. (Ее можно найти в патентной заявке Цузе. [14]).
Инструкция отображения на дисплеи осуществляется с помощью итеративных умножений или делений на 10. Если бинарная экспонента в регистре R1 положительная, то число умножается на 0.1 столько раз, сколько требуется, что бы сделать двоичную экспоненту равной двум и пока 4 левых разряда регистра Bf содержат число от 0 до 9 (0000 и 1001). Это десятичное число, которое может быть отображено в следующей колонке панели вывода. Число вычитается из мантиссы в Bf и процесс продолжается со следующей цифрой. Если бинарная экспонента в R1 отрицательная, то процесс схож, за тем исключением, что осуществляется умножение на 10.
Теперь рассмотрим детальную диаграмму Z3, изображенную на рис. 8. Устройств управления и панели ввода/вывода были рассмотрены ранее. Заметим, что 4 десятичные цифры клавиатуры ввода перемещаются в регистр Ba через блоки переключателей Za, Zb, Zc и Zd, которые активируются друг за другом.
Блоки переключателей Eg и Ei используются для загрузки некоторых используемых констант в регистры экспоненты (+13 и -4, которые используются для преобразования системы счисления). Сдвигающее устройство Ee между регистром Af и регистром Aa используется в алгоритме извлечения квадратного корня. Экспонента результата (Aa) становится равной половине экспоненты исходного числа (Af).
Ah1 является переключателем с двумя состояниями. Когда он в нуле, пара регистров <Af,Bf> доступна для загрузки операндов. Этот переключатель сбрасывается в нуль управляющей линией ai. Управляющие линии al, aj, bl и bj используются для очистки регистра Af, Ab, Bf и Bb при необходимости.
Блок названный «нуль, бесконечность» под Ae представляет собой схемы обработки исключений. Они непрерывно отслеживают шину данных (результаты операций и данных из памяти) и при необходимости устанавливают соответствующие флаги исключений. Сдвигающее устройство под Be используется для сдвига мантиссы на один разряд вправо. Это нужно для нормализации, в случаях когда Be >= 2.
Переключатели Fp и Fq управляют количеством и направлением сдвига в сдвигающем устройстве под блоками переключателей Fc и Fa. Переключатели Fh, Fi, Fk, Fl и Fm выполняют схожую функцию на другом сдвигающем устройстве. Эти 5 разрядов представляют число от -16 до 15, что соответствует диапазону второго сдвигающего устройства. После осуществления сдвига, число представляемое переключателями с Fh по Fm перемещается через блок переключателей Bn в регистр Ab в соответствии с алгоритмом изменения экспоненты результата. Если число сдвигается на 10 разрядов влево, то +10 вычитается из экспоненты результата. Такие большие сдвиги нужны, в основном, после вычислений.
Взглянем снова на схему машины Z3. Все в этой машине похоже на современный микропроцессор с плавающей точкой. Поразительно, как Цузе смог найти столь хорошее архитектурное решение на самой заре вычислительных машин. Процессор Z3 включает всего 600 реле; на память уходит в три раза больше. С целью оптимизировать структуру без возможности изменить аппаратное обеспечение Цузе был вынужден все время переосмысливать логическую структуру машины. Ему была не доступна такая роскошь, как неограниченное финансирование выделяемое министерством обороны США на разработку ENIAC или корпорацией IBM на Mark I. Он был один. Не смотря на то, что это давало ему преимущество на концептуальной стороне, это так же приносило свои минусы, учитывая сколь низкое влияние оказывали машины Z1 и Z3 на зарождающуюся в США компьютерную отрасль после Второй мировой войны. [13]
Основным недостатком Z3 является полное отсутствие условных переходов во множестве инструкций. Когда программа хранится на перфоленте, возможным путем решения этой проблемы является введение нескольких лент и механизма, позволяющего переключаться между лентами (как было с делано в Гарвардской Mark I). Другим путем является использование программного счетчика, чтобы перфолента могла быть перемотана вперед и назад по требованию.
Иногда грань между Вычислительными машинами и Универсальными компьютерами проводится на основе способа хранения программ (внешнего и внутреннего). Я считаю, что этот критерий не является подходящим. Внешняя программа может работать как интерпретатор числовых данных. Внешняя программа становится постоянной частью процессора, а данные становятся программами, таким же образом, каким Универсальная машина Тьюринга работает как интерпретатор. Я считаю, что необходимым условием Универсального компьютера является минимальный набор инструкций и косвенная адресация.[11] Косвенная адресация может симулироваться написанием само-модифицируемой программы, таким образом набор инструкций становится определяющим критерием. Машина с достаточным количеством адресуемой памяти, аккумулятором и способная исполнять инструкции CLR(очистить), INC(инкремент), LOAD, STORE и BZ(ветвление, если нуль) является Универсальным компьютером. В этом случае, машина Z1 не была полноценным компьютером, но такими же было и множество других ранних компьютеров. Машина ABC являлась специализированной машиной, для решения систем линейных уравнений методом Гаусса. Гарвардский Mark I не обладал условным переходом, хотя реализовывал циклы. ENIAC не была программируемой — потоки данных между строительными блоками задавались аппаратно. Условные переходы были доступны с ограничениями, а о само-модифицируемых программах, само собой, и речи быть не могло.
Таблица 9. Сравнение архитектурных особенностей
Таблица 10. Некоторые дополнительные архитектурные особенности
Таблицы 9 и 10 демонстрируют наиболее значимую информацию о ранних вычислительных машинах, упоминаемых выше. Как должно быть ясно из таблиц, ни одна из ранних вычислительных машин не удовлетворяла всем условиям Универсального компьютера. Я так же упомянул Манчестерский Mark I, строившийся с 1946 по 1948 потому, что, насколько я знаю, это первая машина, полностью соответствующая моим условиям Универсального компьютера. Машина Mark I строилась под руководством Фредерика Уильямса( F.C. Williams ) и Тома Килберна (T. Kilburn). Она хранит свою программу в памяти с произвольным доступом реализованной на электронно-лучевой трубке. Все необходимые элементарные инструкции доступны (в модифицированной форме), и несмотря на то, что в ней отсутствует косвенная адресация, в ней может быть реализованы само-модифицируемые программы. Первая программа была запущена в июне 1948, которая рассчитывала наибольший собственный делитель большого числа. В сентябре 1948, Тьюринг получил звание Reader в математическом департаменте Манчестерского университета и написал несколько программ для первого универсального компьютера в мире. Его видение универсального компьютера было опубликовано в 1936, в тот же год, когда было завершено запоминающее устройство Z1. Таблицы 9 и 10 выражают, что изобретение компьютера было коллективным достижением и охватывает 12 лет.
Расшифровка схематической документации была возможна только в сотрудничестве с некоторыми из в моих студентов в университетах в Галле и Берлине. Я благодарю Александра Турма (Alexander Thurm) и Алекса Бауера (Axel Bauer), реализовавших gata-level симулятор процессора Z3. Мы поняли, что такое проблема синхронизации, когда симулятор отказывался запускаться. Так же благодарю Франца Конечного (Franz Konieczny), Реймунда Шпитцера (Reimund Spitzer) и Роланда Шультса (Roland Schultes), написавших часть stand-alone симулятора процессора. Мы начали работать на Z3 с помощью Конрада Цузе, охотно отвечающего на наши вопросы. Мы были поражены, как после более чем 60 лет, вся конструкция Z3 сохраняется у него в голове. С сожалению, Цузе умер в декабре 1995, до того как описание его работы было завершено. Эта работа посвящена его памяти.
Эта статья представляет детальное описание архитектуры вычислительных машин Z1 и Z3, разрабатываемых Конрадом Цузе в Берлине с 1936 по 1941 гг. Информация была в основном получена из детального изучения патента, поданного Цузе в 1941 г. Более глубокая оценка была получена из программной симуляции машинной логики. Z1 была основана исключительно на механических компонентах, а в Z3 использовались электромеханические реле, но обе машины имели общую логическую структуру и программную модель. Z1 и Z3 обладали такими свойствами современных вычислительных машин как: разделение памяти и процессора, способность оперировать числами с плавающей запятой, вычислять 4 основные арифметические операции и квадратный корень. Программы хранились на перфоленте и считывались последовательно. В последующей статье я рассмотрю архитектуру Z1 и Z3 в исторической перспективе, и произведу сравнение с компьютерами построенными в других странах.
Введение
Конрад Цузе признается в Германии как отец компьютера, и его Z1, программируемый автомат, строящийся с 1936 по 1938 гг., считается первым компьютером в мире. В других странах это значение придается другим ученым, и там проходят долгие и острые споры по вопросу, кто является истинным изобретателем компьютера. Иногда споры переходили в глубокие и детальное описание технологических особенностей конкретных машин. К примеру ENIAC ( Electronic Numerical Integrator and Computer ) считается «Первой широкомасштабной, полностью электронной вычислительной машиной в мире». ENIAC строился в Школе Электротехники Мура при Пенсильванском университете (Moore School of Electrical Engineering of the University of Pennsylvania ) с 1943 по 1945 гг. Он решил первую задачу в декабре 1945 и был представлен в феврале 1946. Другим кандидатом на титул первого компьютера считается Mark I, строящийся Говардом Айкеном в Гарвардском университете с 1939 по 1944 гг. Mark I был электромеханической машиной, т.е. построенной не на чисто механических элементах, как в более ранних вычислительных устройствах, и не на электронике, уже доступной в то время. В машине Джона Атанасова (позже названной ABC) из Государственного Колледжа штата Айова, строящейся с 1939 по 1944, использовались вакуумные трубки, но при этом машина имела ограничения на сложение и вычитание векторов, и имеющаяся структура не подходила для универсальных вычислений. Z1 является прямой противоположностью этих машин, более гибкая, построенная для исполнения длинных и модифицируемых последовательностей инструкций, считываемых с перфоленты. Машины Z3 и Z4 не были электронными и обладали меньшими габаритами. Z3 была построена и успешно прошла испытания раньше чем Mark I, и поэтому была названа первой программируемой вычислительной машиной в мире. Конечно давние дискуссии не будут завершены на этой статье, но я хочу показать, насколько передовыми были машины Цузе, с точки зрения современной компьютерной архитектуры и по сравнению с архитектурой того времени.
Цузе, будучи студентом Берлинского политехнического, начал работать над вычислительной машиной в 1930х. Он понял, что может построить автомат способный выполнять последовательность математических операций, которые требуются для построения математических таблиц. Придя из гражданской инженерии, он имел опыт в области электроники, но не был знаком с технологиями, используемыми в обычных механических калькуляторах. Однако эта нехватка знаний дала ему преимущество, т.к. он смог переосмыслить все вопросы машинной арифметики и найти новые оригинальные решения.
Цузе решил построить свою первую экспериментальную вычислительную машину основываясь на двух главных идеях:
- Машина должна работать в двоичной системе счисления
- Вычисляемые и Управляющие данные должны быть разделены в памяти
Годом ранее Джон фон-Нейманн объяснял преимущество компьютерной архитектуры с процессором, разделяющим память. Цузе пришел к такому же выводу. Надо заметить, что Чарльз Бэббидж пришел к тем же выводам проектируя свою Аналитическую машину в прошлом столетии. В 1936 г. Цузе закончил работу над памятью для своей машины, и назвал ее Speicherwerk (нем. — Запоминающие устройство) — термин Speicher использовался в Германии вместо антропоморфного термина Memory (англ. — Память), который ввел фон-Нейманн, Бэббидж же использовал термин Store (англ. — Хранилище). Память являлась механическим устройством, но не обычного типа. Вместо использования шестеренок (их использовал Бэббидж в прошлом веке), Цузе реализовал логические и арифметические операции на скользящих металлических рейках. Рейки могли перемещаться в одном из двух направлений (прямое и обратное) и следовательно являлись двоичным механизмом. Процессор Z1 был построен спустя 5 месяцев после построения памяти. При работе с памятью он был крайне ненадежным. Главная проблема была в точности синхронизации, которая требуется для предотвращения чрезмерной механической нагрузки на подвижные части. Интересно отметить, что в том же году, когда Цузе закончил работать над памятью, Алан Тьюринг написал свою новаторскую работу On computable numbers (англ. — О вычислимых числах), в которой формализовал интуитивно понятные вычисления.
Машина Z1, несмотря на ненадежность, показала, что Архитектурный дизайн был целесообразным и побудила Цузе изучить другие виды технологий. Следуя совету своего друга Хельмута Шряера, он рассмотрел электромеханические реле. Цузе построил «промежуточную» модель ( Z2 ) на смешанной технологии (процессор строился на реле, а память осталась механической). В 1938 г. Цузе начал разработку Z3, машину полностью построенную на реле, но с логической структурой от Z1. Она была готова к эксплуатации в 1941 г., за 4 года до ENIAC.
Эта работа предполагает детальное рассмотрение архитектуры машин Z1 и Z3. Цузе реконструировал свою машину Z1 в Берлине в 80х годах, и сейчас она выставляется в Берлинском музее транспорта и технологий. Однако доступная информация описывает устройство механической памяти[12]. Цузе документировал Z3 в патентном приложении Z-391 1941г, но его анализ затруднен из-за нестандартной нотации и терминологии[14]. Книга [4] о Z3 является хорошим источником для понимания исторической обстановки, окружающей исследования Цузе, но не описывает Z3 в деталях. Т.к. Z1 и Z3 эквивалентны с логической и функциональной точки зрения, в дальнейшем, я буду ссылаться только на Z3. Основным архитектурным отличием является то, что Z1 нет поддержки операции извлечения квадратного корня. Остальные минимальные отличия сводятся к различаю в количестве бит в арифметических операторах процессора (Z1 использует меньшую разрядность мантиссы в числах с плавающей запятой) и в количестве циклов необходимых для каждой инструкции. С минимальной оговоркой, принимая во внимание только архитектуру, можно считать Z1 и Z3 эквивалентными машинами. Проводились споры, действительно ли реконструированная Z1 соответствует оригинальной Z1, уничтоженной во время второй мировой войны. Цузе реконструировал машину Z1 основываясь исключительно на свои воспоминания, и вполне возможно, что реконструированная машина имеет больше общего с Z3, чем с оригинальной Z1. Так же, Цузе указывает в своих мемуарах на базовое сходство Z1 и Z3 [15], и подтверждает этот аспект своей работы в частном интервью.
Обзор архитектуры Z1 и Z3
В этом разделе большинство архитектурных особенностей приведены для Z3. Вначале я представлю обзор архитектуры, потом перейду к деталям.
Структурная схема
Z3 работала с числами с плавающей запятой, в отличие от других ранних вычислительных автоматов, таких как Mark I, ABC или ENIAC, работающих с числами с фиксированной запятой. Цузе разработал то, что позже назвал «полулогарифмическая запись», которая соответствует современному представлению чисел с плавающей запятой.
На рис. 1 изображены основные составные блоки Z3. Первой особенностью архитектуры является разделение процессора и памяти. Z3 включает двоичную память (способной хранить 64 числа с плавающей запятой), двоичный процессор для чисел с плавающей запятой, устройство управления и устройства ввода/вывода. Память и Арифметический блок соединены шиной данных, передающей экспоненту и мантиссу числа с плавающей запятой. Устройство управления содержит микропрограммы для каждой инструкции. Управляющие сигналы поступают в процессор, память и устройство ввода/вывода для осуществления синхронизации всех блоков. Устройство чтения перфоленты предоставляет код операции для каждой инструкции, а так же адрес для доступа к памяти. Устройство ввода/вывода подключено к процессору шиной данных.

Представление чисел с плавающей запятой
На рис. 2 изображено представление используемое в Z3. Первый разряд используется для хранения знака, следующие 7 разрядов хранят экспоненту, а последние 14 разрядов хранят мантиссу. Разряды экспоненты называются Часть А и обозначаются как a6,...,a0. Разряды мантиссы называются Часть B и обозначаются как b0,b-1,...,b-14. Экспонента закодирована в дополнительном коде и может содержать значения в диапазоне от -64 до 64. Мантисса хранится в нормализованной форме, в которой первый разряд после запятой (b0) всегда должен быть установлен единицу [5]. Этот разряд не хранится в памяти (поэтому он не показан на рис. 2), так что эффективный диапазон значений мантиссы в памяти равен 15 битам. Однако возникает проблема с числом 0, т.к. нормализованная мантисса не может его выразить. В Z3 существует соглашение, согласно которому, любая мантисса с экспонентой -64 рассматривается как 0. Любое число с экспонентой равной 63 считается бесконечно большим. Операции над 0 или бесконечно большим вызывают исключения, и специальные аппаратные контроллеры устанавливают в процессоре флаги исключения (рассмотрим ниже).
Учитывая это соглашение, минимальным числом в памяти Z3 является 2-63 = 1.08x10-19, а максимальным 1.999x262 = 9.2x1018. Аргументы для расчета могут вводиться в виде десятичных чисел с клавиатуры (четырехзначные). Экспонента десятичного представления вводится нажатием соответствующей кнопки в ряду кнопок помеченных -8,-7,...,7,8. Оригинальная Z3 позволяла вводить только числа в диапазоне от 1x10-8 до 9,999x108. Реконструированная Z3 из Германского музея в Мюнхене имеет дополнительные кнопки для больших экспонент. С этим улучшением стало возможно вводить полный числовой диапазон машины с клавиатуры. Немного скажем о выводе. Z3 не печатала результаты программных процедур. Единственное число отображалось на массиве ламп, представляющих числа от 0 до 9. Максимальным числом, который Z3 была способна отобразить являлось 19,999, а минимальным 00001. Максимальной отображаемой экспонентой было +8, а минимальной -8.

Набор инструкций
Программа Z3 хранится на перфоленте. Одна инструкция использует 8 разрядов из каждого ряда на ленте. Набор инструкций Z3 состоит из 9 инструкций представленных в таблице 1. Они поделены на 3 группы: ввод/вывод, память и арифметические операторы. Код операции имеет переменную длину от 2х до 4х разрядов. Операторы памяти кодируют адрес слова в младших 6 разрядах, которые способны адресовать 64 слова, как упоминалось ранее.
Инструкции на перфоленте могут располагаться в любом порядке. Инструкции Lu и Ld (Чтение с клавиатуры и Отображение на дисплей) останавливают машину, чтобы у оператора было достаточно времени для ввода числа и записи результата.
Z3 не имеет инструкций условных переходов. Циклы реализуются простым скреплением двух концов перфоленты, но это не позволяет реализовывать условные последовательности инструкций. Следовательно Z3 не является универсальным компьютером в описании Тьюринга.
Таблица 1. Множество инструкций и их кодов машины Z3
| Тип | Инструкция | Описание | КОП |
| В/в | Lu | Ввод с клавиатуры | 01 110000 |
| Ld | Вывод результат | 01 111000 | |
| Память | Pr z | Загрузить с адреса z | 11 z6z5z4z3z2z1 |
| Ps z | Записать по адресу z | 10 z6z5z4z3z2z1 | |
| Арифметические | Lm | Умножение | 01 001000 |
| Li | Деление | 01 010000 | |
| Lw | Квадратный корень | 01 011000 | |
| Ls1 | Сложение | 01 100000 | |
| Ls2 | Вычитание | 01 101000 |
Число циклов
Z3 является синхронной машиной. Каждый цикл разделен на 5 стадий, называемых I, II, III, IV и V. На стадии I происходит декодирование инструкции с перфоленты. Основными арифметическими операциями являются сложение и вычитание экспоненты и мантиссы. Операции могут исполняться в первых трех стадиях каждого цикла. Стадии IV и V используются для подготовки аргументов к следующим операциям или вывода результата.
Таблица 2. Число циклов, необходимых для выполнения инструкций
| Операция | Число циклов |
| Умножение | 16 |
| Деление | 18 |
| Квадратный корень | 20 |
| Сложение | 3 |
| Вычитание | 4 или 5, зависит от результата |
| Ввод с клавиатуры | от 9 до 41, зависит от экспоненты |
| Вывод результата | от 9 до 41, зависит от экспоненты |
| Загрузка из памяти | 1 |
| Запись в память | 0 или 1 |
По словам Цузе, умножение выполняется за 3 секунды. Учитывая то, что операция умножения требует 16 циклов, можно оценить, что рабочая частота Z3 составляет 3/16 = 5,33 Гц. Любопытно то совпадение, что симулятор Z3, который мои студенты реализовали на персональном компьютере, тоже требует около 3х секунд для умножения.
Число циклов необходимых для инструкций Ввода с клавиатуры и Вывода на дисплей переменно, потому что зависит от экспоненты аргументов. Т.к. ввод должен преобразовывать десятичное представление в двоичное, количество умножений на 10 или 0,1 определяется значением десятичной экспоненты (рассмотрим ниже).
Сложение и вычитание требуют больше одного цикла потому, что в случае с числами плавающей запятой, нам необходимо привести экспоненты обоих аргументов к одному значению. Это требует дополнительных сравнений и сдвигов.
Число может быть записано в память за 0 циклов в том случае, когда результат последней арифметической операции может быть перенаправлен на требуемый адрес памяти. В этом случае цикл, необходимый для инструкции записи, совпадает с последним циклом арифметической операции.
Программная модель
Очень важно описать машину Z3 с точки зрения программиста. С точки зрения программного обеспечения, Z3 состоит из 64 слов в памяти, способных загружаться в 2 регистра с плавающей запятой, которые я для простоты назову R1 и R2. Два регистра хранят аргументы для арифметической операции. Программист может писать любые последовательности инструкций, но должен помнить о состоянии регистров.
Важно помнить последовательность: Первая операция загрузки в программе (Pr z) загружает содержимое адреса z в R1. Все последующие операции загрузки загружают слово из памяти в R2. Инструкция Ввода с клавиатуры загружает число в R1 и ОЧИЩАЕТ R2, который используется как временное значение при преобразовании десятичного ввода в двоичное представление.
Арифметические операции не содержать аргументов в коде операции. Всегда используются следующие аргументы:
| Умножение | R1 := R1 * R2 |
| Деление | R1 := R1 / R2 |
| Сложение | R1 := R1 + R2 |
| Вычитание | R1 := R1 — R2 |
| Квадратный корень | R1 := sqrt(R1) |
R2 сбрасывается в 0 после арифметический инструкций, записывающих результат в R1. Последующие операции загрузки из памяти отсылают значение в R2. Инструкции записи в память и вывода на дисплей всегда берут значение из R1, который содержит результат последней арифметической операции. После операций сохранения или вывода, R1 сбрасывается в 0 (при отключении реле, которые потом будут готовы к принятию нового значения). Следующая загрузка из памяти происходит в R1.
Приведем пример для лучшего понимания программной модели Z3. Предположим, нам требуется рассчитать полином методом Горнера.
x ( a2 + x ( a3 + x a 4)) + x5
Далее будем считать, что аргументы a4, a3, a2 и a1 хранятся в четвертой, третей, второй и первой ячейках памяти соответственно. Значение z хранится в пятой. Программа приведена ниже:
Pr 4 загрузить a4 в R1 Pr 5 загрузить x в R2 Lm умножить R1 и R2, результат в R1 Pr 3 загрузить a3 в R2 Lsl сложитьR1 и R2, результат в R1 Pr 5 загрузить x в R2 Lm умножить R1 и R2, результат в R1 Pr 2 загрузить a2 в R2 Lsl сложитьR1 и R2, результат в R1 Pr 5 загрузить x в R2 Lm умножить R1 и R2, результат в R1 Pr 1 загрузить a1 в R2 Ls1 сложитьR1 и R2, результат в R1 Ld вывести на дисплей результат
После исполнения последней инструкции процессор сбрасывается с исходное
состояние.
Блочная диаграмма Z3
В это разделе, я рассмотрю структуру Z3 и опишу основные составные блоки в
деталях. Важно показать, как осуществляется синхронизация между
компонентами.
Процессор
На рис. 3 изображена упрощенная схема арифметического устройства. Он состоит из двух частей: левая осуществляет операции над экспонентой числа с плавающей запятой, а правая — операции над мантиссой. Регистры Af и Bf хранят экспоненту и мантиссу того, что с программной точки зрения называется R1. Я буду представлять R1, как пару регистров < Af, Bf>. Пара регистров < Ab, Bb> хранит экспоненту и мантиссу R2. Пара < Aa,Ba> хранит экспоненту и мантиссу третьего временного регистра с плавающей запятой, невидимого для программиста. Два Арифметико-логических устройства (АЛУ) A и B используются для сложения и вычитания экспонент и мантисс, соответственно. Экспонента и мантисса результата помещаются в Ae и Be соответственно. Пара < Ae, Be> рассматривается как внутренний регистр, недоступный для программиста. В части B, мультиплексор позволяет выбрать результат операции между Ba и выходом АЛУ. Мультиплексор управляется с помощью переключателя Bt (если Bt=0, то Be получает значение Ba).

Маленькие блоки обозначенные Ea, Eb, Ec, Ed, Ef, Fa, Fb, Fc, Fd и Ff являются релейными блоками (далее РБ), открывающими и закрывающими шины. К примеру, чтобы предать значение содержимое регистра Af в регистр Aa, необходимо установить РБ Ea в единицу. Как мы можем видеть из рис. 3, содержимое Af может быть перенесено в Aa или Ab, а содержимое Ae может быть перенесено в Aa, Ab или Af, в зависимости от состояния РБ. Часть B арифметического устройства устроена аналогично, но с добавлением мультиплексора управляемого переключателем Bt и сдвигающих устройств между Bа и Ba, и между Bf и Bb. Первое сдвигающее устройство может сдвигать мантиссу в пределах 2 разрядов влево или 1 разряда вправо. Оно осуществляет деление Bf на 4 или умножение на 2. Второе сдвигающее устройство способно сдвинуть Af на одну из 16 позиций влево или одну из 15 позиций вправо. Эти сдвигающие устройство требуется для сложения и вычитания чисел с плавающей запятой. Операции умножения и деления на степени двойки могут осуществляться с последующей арифметической операцией без затрат дополнительного времени.
Таблица 3. Разрядность регистров
| Af | 7 разрядов | Bf | 17 разрядов |
| Aa | 8 | Ba | 19 |
| Ab | 8 | Bb | 18 |
| Ae | 8 | Be | 18 |
Как мы можем видеть из списка, Ae имеет дополнительные разряд для сохранения результата сложения экспонент аргументов. Часть B имеет 2 дополнительных разряда (b-15 и b-16) и явный разряд b0, не хранящийся в памяти. -15 и -16 разряды введены для увеличения точности вычислений. Следовательно, общая разрядность, необходимая для хранения результата арифметических операций в Bf, составляет 17 бит. Регистрам Ba и Bb требуется дополнительные разряды (ba2, ba1 и bb1) для хранения промежуточных результатов некоторых вычислений. Например, для алгоритма расчета квадратного корня может потребоваться 3 разряда слева от десятичной запятой.
Простейшей операцией над каналом данных является сложение и вычитание мантиссы и экспоненты. Когда переключатели As или Bs установлены в 1, АЛУ переводит второй аргумент в дополнительный код, т.е. меняет его знак (Ab или Bb). Следовательно, если переключатель As установлен в 1, то АЛУ части A осуществляет вычитание, в противном случае сложение. Часть B и переключатель Bs работают аналогично.
Предположим имеется два числа с равными экспонентами, которые необходимо сложить. Первая экспонента хранится в Af, а вторая в Ab. Поскольку они равны, эта часть машины не должна производить никаких операций. В части B, мантисса первого числа хранится в Bf, а мантисса второго в Bb. Первый этап состоит в переносе числа из Bf в Bf, для чего необходимо установить релейный блок Fa в 1. Далее происходит сложение. Для того чтобы результат Ba+Bb записался в Be, необходимо установить переключатель Bt в 1. РБ Ff в настоящий момент установлен в 1, и результат помещается в Bf. Архитектура должна предоставлять правильную последовательность воздействий на переключатели для исполнения желаемой операции. Z3 осуществляет это благодаря технике, очень похожей на микропрограммирование.
Устройство управления
На рис. 4 изображена детальная схема устройства управления и панелей ввода/вывода. Схема Pa декодирует код операции, считаный с перфоленты. Если это инструкция памяти, то схема Pb посылает на шину адреса младшие 6 бит из кода операции. Устройство управления определяет микропоследовательности инструкций. Для каждого оператора из набора инструкций имеется специальные схемы.
Схема Z представляет клавиатуру, используемую для ввода десятичных чисел. Только одна кнопка в каждом из четырех столбцов может быть нажата. Экспонента устанавливается нажатием одной из кнопок, помеченных от -8 до 8, на схеме K. Дисплей очень похож на панель ввода, его лампы высвечивают принятое десятичное число, и его экспоненту (схема Q). Обратите внимание, что на дисплее выводится пятая цифра (может принимать значения только 0 или 1).
После ввода десятичного числа, оно передается по шине данных в регистр Ba, и начинает выполнятся специальная последовательность операций. Десятичное число, введенное с клавиатуры, должно быть преобразовано в двоичное представления. Для этого требуется произвести несколько умножений, количество которых определяется значением экспоненты. Для экспоненты равной нулю, на полное преобразование затрачивается 9 циклов, а для экспоненты равной -8, затрачивается 9+4*8 = 41 цикл.

Микроуправление Z3
В основе Устройства управления лежит контроллер микропоследовательностей. Перед рассмотрением принципа его работы, нам необходимо подробно рассмотреть алгоритмы арифметических инструкций Z3. На рис. 5 показана основная идея. Каждый цикл состоит из 5 стадий. На стадиях IV и V осуществляется ввод информации в машину. На стадиях I, II и III происходит сложение/вычитание, в частях A и B. Я назвал эту фазу инструкции — «исполнение». Типичная инструкция осуществляет выборку аргументов, исполнение и запись результата. Цузе удалось сократить время исполнения за счет перекрытия стадий выборки аргументов для следующей инструкции и записи результата текущей. В итоге можно считать, что исполнительный цикл состоит из двух этапов (на рис. 5 обозначены первые два цикла).
Контроллер микропоследовательностей реализован с помощью специального управляющего колеса. Реализованы отдельные колеса для алгоритма умножения, деления и взятия квадратного корня. Подвижный рычаг, изображенный на рис. 6, начинает вращаться по часовой стрелке, как только устройство управления декодирует соответствующую инструкцию. За каждый цикл рычаг перемещается на одну позицию. Рычаг проводит электричество и активирует схемы с которыми приходит в контакт. В примере изображенным на рис. 6, подвижный рычаг устанавливает переключатель Ea в 1 на первом цикле. Это ведет к переносу числа из регистра Af в Aa. На следующем цикле, активизируются переключатели Ec и Fc. В этом случае результаты операции в частях A и B записываются в регистры Aa и Ba, соответственно. Как мы можем видеть, использование таких колес управления предоставляет платформу для легкой модификации микропоследовательностей определенных операторов. Аналогично устроены контроллеры микропоследовательностей в современных микропроцессорах. Я не назвал этот способ микропрограммированием, потому что в нашем случае контроллер микропоследовательностей является аппаратным, но очевидно, что микропоследовательности и микропрограммы тесно связаны.


Использование контроллеров микропоследовательностей позволило Цузе сильно упростить машину. После того, как основные схемы были готовы на их основе совершенствовалось устройство управления, пока не удалось достичь оптимальной последовательности микрокоманд. Инженер, проектируя «микропрограмму», должен учитывать множество деталей, иначе короткое замыкание может уничтожить машину. Механическая Z1 была более чувствительна в этом отношении, чем Z3. По завершению этого этапа был список последовательностей, которые программист должен избегать, что бы не допустить порчу оборудования. Одна из таких последовательностей по неосторожности была запущена в Берлинском музее технологий и транспорта, и привела к небольшим повреждениям реконструкции Z1 в 1994 г.
Сумматоры
Важной особенностью сумматора Z3, является вычисление суммы и разности методом, называемом схемой ускоренного переноса. Если бинарное сложение осуществляется прямым образом, перенос передается от каждого разряда на один бит далее. В случае с мантиссой, требуется 16 циклов для передачи переноса одного разряда. Сложение в реализации Цузе значительно быстрее, где сложение и вычитание осуществляется в течении I, II и III фазах одного цикла. Для вычитания второй аргумент переводится в обратный код с добавлением единицы к младшему разряду (дополнительный код).
Рассмотрим сложение регистров Ba и Bb. Я буду обозначать i-ый разряд регистра Bb как bbi или Bb[i]. В такой нотации будут обозначаться все регистры. Первый промежуточный результат получается поразрядным Исключающим ИЛИ между двумя регистров, т.е. bci=bai XOR bbi. Второй промежуточный результат получается поразрядной конъюнкцией между двумя регистрами, т.е. bai AND bbi. Следующая операция находит разряды, для которых требуется перенос. Промежуточный результат bdi вычисляется по схеме, изображенной на рис. 7. Обратите внимание, что если разряд установлен в единицу, то по соответствующей линии переноса идет ток, в противном случае источник питания отключен (что бы не произошло короткое замыкание). Схема подключения переключателей bc1,...,bc-16 показана на рис. 7. Если разряд bci установлен в единицу, соответствующий переключатель разомкнут. Итоговый результат равен bei = bdi XOR bci. Подобная схема позволяет переместить перенос на последний разряд значительно быстрее. В случае, если все переключатели активны, перенос перемещается от первого разряда к последнему не затрачивая времени.

Числовые алгоритмы
В этом разделе я опишу алгоритмы над числами с плавающей запятой, используемые в Z3. Все они, без исключения, используются в обычных маленьких последовательных процессорах с плавающей запятой.
Исключения чисел с плавающей запятой
Основной проблемой записи с плавающей запятой является соглашение, касательно представления числа 0. Z3 решает эту проблему с помощью исключений (переполнение и потеря разрядов) для отслеживания значения экспоненты после арифметических операций или операции загрузки из память. Специальные схемы следят за состоянием шины Ae и перехватывают исключения. Любое число с экспонентой -64 является 0: Переключатель обозначаемый Nn1 устанавливается в 1, если такое число хранится в паре регистров < Af,Bf>. Если такое число хранится в паре регистров < Ab,Bb>, переключатель Nn2 устанавливается в 1. Поэтому, мы всегда знаем, является-ли один из аргументов арифметической операции нулем. Нечто подобное происходит для любого числа с экспонентой 63 (бесконечно большое). В это случае, переключатели Ni1 или Ni2 сбрасываются в 0, если соответствующие пары регистров хранят такие числа.
Операции включающие «исключительные» числа (нуль и бесконечность) производятся как обычно, но с помощью специальной схемы результат подменяется. Рассмотрим, к примеру, умножение с первым аргументом равным нулю (Nn1 установлен в 1). Вычисление проходит как обычно, но в каждом цикле специальная схема выдает результат -64 из сумматора Части A. Совершенно не важно, какие операции проводились с мантиссой, поскольку экспонента равна -64, а значит и конечный результат равен нулю. Деление на нуль происходит аналогично. Z3 может обнаружить неопределенности, такие как 0/0, ∞-∞, ∞/∞ и 0*∞. Во всех этих случаях загорается индикатор соответствующего исключения на панели вывода и машина останавливается. Z3 всегда вычисляет правильный результат, когда один из аргументов является нулем или бесконечностью, а второй конечным ненулевым числом. Но это не относится к Z1. Цузе думал об обработке исключений в Z1, но она так и осталась не реализованной. Машина выдает неверный результат в некоторых вычислениях с нулем.
Дополнительная схема смотрит на экспоненту результата, на выходе из сумматора Части А. Если экспонента больше или равна 63, то произошло переполнение и результат должен быть установлен в бесконечность. Если экспонента упала до -64, то произошла потеря разрядов и результат должен быть установлен в нуль. Для этого соответствующие переключатели (Nn1 или Ni2) устанавливаются в 1.
Цузе реализовал обработку исключений используя всего 5 реле. Эта особенность Z3 является одной из самых элегантных во всем дизайне. Большинство ранних микропроцессоров в 1970х не обладали обработкой исключений и реализовывали их программно. Подход Цузе более совершенный, поскольку он освобождает программистов от необходимости все время проверять границы чисел перед каждой операцией.
Сложение и Вычитание
Для сложения или вычитания двух чисел с плавающей запятой x и y, они должны быть представлены с одинаковой экспонентой. После этого сложение и вычитание осуществляется только над мантиссой. Если экспоненты отличаются, мантисса меньшего числа сдвигается вправо на необходимое количество разрядов ( а экспонента соответственно инкремируется так, чтобы операнд сохранял свое значение ), чтобы экспоненты сравнялись. Конечно может случиться так, что меньшее число станет нулем после 17 смещений вправо.
Знаки операндов сравниваются перед принятием решения о типе выполняемой операции. Если запрошено сложение, то выполняется сложение в случае одинаковых знаков и вычитание в случае различных знаков. Если запрошено вычитание и знаки одинаковы, то выполняется вычитание, а если различны то выполняется сложение.
Специальная схема устанавливает знак результата исходя из знаков операндов и знака промежуточного результата.
Сложение и вычитание управляется цепью переключателей (а не Колесом управления микропоследовательностями), т.к. пока максимальное число необходимых этапов не велико. В таблице 4 приведены сигналы, необходимые для сложение двух чисел. Изначально аргументы операции сложения хранятся в парах регистров < Af, Bf> и < Ab,Bb>. На первом цикле экспоненты сравниваются. На втором цикле мантисса числа с большей экспонентой загружается в регистр Ba, а мантисса числа с меньшей экспонентой загружается в регистр Bb. Мантисса в регистре Bb сдвигается вправо на число равное абсолютному значению разности экспонент (система обработки исключений заботится о случае, когда меньшее число становится нулем после сдвига). На стадиях I, II и III второго цикла, мантиссы складываются и в конце процессор проверят, является ли результат большим двух. Если является, мантисса сдвигается на одну позицию вправо, а экспонента инкремируется. Важно заметить, что проверка «if(Be > 0)» осуществляется в Части А арифметического блока после того, как Be будет вычислена в Части B на стадиях I, II и III цикла 2.
Таблица 4. Циклы алгоритма сложения
| Цикл | Стадия | Экспонента | Мантисса |
| 0 | I, II, III | ||
| 1 | IV, V | Aa := Af |
|
| I, II, III | Ae := Aa — Ab |
Be := 0 + Bb |
|
| 2 | IV, V | If( Ae >= 0 ) then Ab:=0, Aa:=Af else Aa:=0 |
If( Ae >= 0 ) then Ba:=Bf, Bb:=Be(shifted) else Ba:=Be, Bb:=Bf(shifted) |
| I, II, III | If( Be>=2 ) then Ae:=Aa+Ab+1 else Ae:=Aa+Ab |
Be:=Ba+Bb |
|
| 3 | IV, V | Af:=Ae |
if(Be>=2) then Bf:=Be/2 else Bf:=Be |
В случае вычитания требуется 4 или 5 циклов. В таблице 5 представлены сигналы, необходимые для операции вычитания. Первые два цикла полностью идентичны первым двум циклам алгоритма сложения, за исключением того, что мантиссы вычитаются. Цикл 3 выполняется только в случае если мантисса результата положительная. Цикл 4 очень важен: разность нормализованных мантисс может иметь много нулей в первых разрядах слева. Результат нормализуется путем сдвига Be влево на необходимое число разрядов (это осуществляется сдвигающим устройством между переключателем Fd и регистром Bb). Число сдвигов вычитается из экспоненты в Части А процессора. В цикле 5 результат записывается в пару регистров <Af, Bf>.
Таблица 5. Циклы алгоритма вычитания
| Цикл | Стадия | Экспонента | Мантисса |
| 0 | I, II, III | ||
| 1 | IV, V | Aa := Af |
|
| I, II, III | Ae := Aa — Ab |
Be := 0 + Bb |
|
| 2 | IV, V | If( Ae >= 0 ) then Ab:=0, Aa:=Af else Aa:=0 |
If( Ae >= 0 ) then Ba:=Bf, Bb:=Be(shifted) else Ba:=Be, Bb:=Bf(shifted) |
| I, II, III | Ae:=Aa+Ab |
Be:=Ba-Bb |
|
| 3 | IV, V | Af:=Ae, Ab:=0 |
Ba:=0, Bb:=Be |
| I, II, III | Ae:=Aa+Ab |
Be:=Ba-Bb |
|
| 4 | IV, V | Aa:=Ae Ab:= Число сдвигов |
Bb:=Be(shifted) (Be нормализован сдвигами влево) |
| I, II, III | Ae:=Aa-Ab |
Be:=0+Bb |
|
| 5 | IV, V | Af:=Ae |
Bf:=Be |
Умножение
Алгоритм умножения Z3 похож на один из методов десятичного умножения на пальцах. Метод основан на повторяющихся сложениях множителя с отдельными цифрами множимого. В начале работы алгоритма первый операнд хранится в паре регистров < Af,Bf>, а второй операнд в паре регистров < Ab,Bb>. Промежуточная пара регистров < Aa,Ba> сброшена в 0. В таблице 6 приведена микропоследовательность, выполняемая Колесом управления микропоследовательностями для осуществления умножения. Алгоритм требует 16 циклов. В умножении участвуют только разряды с -14 по 0. Экспоненты складываются на первом цикле, а результат сложение циклически хранится в Части А Арифметического блока. Мантиссы обрабатываются в Части B. Регистр Ba хранит промежуточный результат вычислений.
Основной цикл умножения имеет следующий вид:
Ba := Be / 2
Be := Ba + Bb * (i-ый бит Bf)
Для i = -14,..,0. Промежуточный результат в Be сдвигается на один разряд вправо для выполнения выражения Ba := Be / 2. Эта операция выполняется в сдвигающем устройстве, подключенном к переключателю Fc.
Результатом умножения мантисс является число 1 < = r < 4 (для операндов в заданных пределах). На последнем цикле результат проверяется на выполнения условия r > = 2. Если условие выполняется, то результат сдвигается на один разряд вправо, а экспонента инкремируется.
Таблица 6. Циклы алгоритма умножения
| Цикл | Стадия | Экспонента | Мантисса |
| 0 | I, II, III | ||
| 1 | IV, V | Aa := Af |
|
| I, II, III | Ae := Aa + Ab |
If( Bf[-14]=1 ) then Be:=Ba+Bb else Be:=Ba |
|
| 2 | IV, V | Aa:=Ae, Af:=0, Ab:=0 |
Ba:=Be/2 |
| I, II, III | Ae := Aa + Ab |
If( Bf[-13]=1 ) then Be:=Ba+Bb else Be:=Ba |
|
| 3 | IV, V | Aa:=Ae |
Ba:=Be/2 |
| I, II, III | Ae:=Aa+Ab |
If( Bf[-12]=1 ) then Be:=Ba+Bb else Be:=Ba |
|
| ... | ... | ... | ... |
| i | IV, V | Ae := Aa + Ab |
Ba:=Be/2 |
| I, II, III | Aa:=Ae |
If( Bf[i-15]=1 ) then Be:=Ba+Bb else Be:=Ba |
|
| ... | ... | ... | ... |
| 15 | IV, V | Af:=Ae |
Ba:=Be/2 |
| I, II, III | if(Be>=2) then Ae:=Aa+1 |
If( Bf[0]=1 ) then Be:=Ba+Bb else Be:=Ba |
|
| 16 | IV, V | Af:=Ae |
If( Be >= 2 ) then Bf:=Be/2 else Bf:=Be Bb:=0 |
Деление
Алгоритм деления очень похож на алгоритм умножения, за тем исключением, что вместо циклического сложения используется циклическое вычитание. В начале работы алгоритма делимое хранится в паре регистров <Af,Bf>, а делитель в паре регистров <Ab,Bb>. Промежуточная пара регистров <Aa,Ba> сброшена в 0. В таблице 7 приведена микропоследовательность выполняемая Колесом управления микропоследовательсностями. Алгоритм требует 18 циклов.
Основная идея алгоритма очень проста. Экспонента результата получается в результате вычитания экспонент делимого и делителя. Теперь о мантиссах: Пусть нам необходимо вычислить x/y для мантисс x и y. Т.к. мы имеем дело с нормализованными числами, то первая цифра результата равна единице, в случае если x >= y, и нулю в случае если x < y. В первом случае мы присваиваем в первую цифру результата 1 и вычисляем остаток, который равен x — y. Остаток рекурсивно делится на y. Для этого он сдвигается на один разряд влево и новый результативный бит сохраняется в регистре Bf на позиции -1 (таким образом компенсируя эффект сдвига). В случае если результативный бит равен нулю, то остаток равен просто x и рекурсивное деление продолжается как и в первом случае.
Основное цикл деления имеет следующий вид:
Ba := 2 × Be
if (Ba–Bb > 0) then Be := Ba–Bb, Bf[i] := 1
else Be := Ba
Bf[i] := 0
Для i = 0,..,-14. Промежуточный результат в Be сдвигается на один разряд влево для выполнения выражения Ba := 2 x Be. Эта операция выполняется в сдвигающем устройстве, подключенном к переключателю Fc.
Результатом деления мантисс является число 1/2 < r < 2. Это условия проверяется в циклах 17 и 18. Если r < 1, то единица вычитается из экспоненты и результат сдвигается на один разряд влево, чтобы получить нормализованное число.
Таблица 7. Циклы алгоритма умножения
| Цикл | Стадия | Экспонента | Мантисса |
| 0 | I, II, III | ||
| 1 | IV, V | Aa := Af |
Ba := Bf |
| I, II, III | Ae := Aa — Ab |
If( Ba-Bb >= 0 ) then Be:=Ba-Bb; bt:=1 else Be:=Ba; bt:=0 |
|
| 2 | IV, V | Aa:=Ae, Ab:=0 |
Bf:=0 if( bt = 1 ) then Bf[0] := 1 Ba:=2 x Be |
| I, II, III | Ae := Aa + Ab |
If( Ba-Bb >= 0 ) then Be:=Ba-Bb; bt:=1 else Be:=Ba; bt:=0 |
|
| 3 | IV, V | Aa:=Ae |
if( bt = 1 ) then Bf[1] := 1 Ba:=2 x Be |
| I, II, III | Ae:=Aa+Ab |
If( Ba-Bb >= 0 ) then Be:=Ba-Bb; bt:=1 else Be:=Ba; bt:=0 |
|
| ... | ... | ... | ... |
| i | IV, V | Aa:=Ae |
if( bt = 1 ) then Bf[2-i] := 1 Ba:=2 x Be |
| I, II, III | Ae:=Aa+Ab |
If( Ba-Bb >= 0 ) then Be:=Ba-Bb; bt:=1 else Be:=Ba; bt:=0 |
|
| ... | ... | ... | ... |
| 16 | IV, V | Af:=Ae |
if( bt = 1 ) then Bf[-14] := 1 Ba:=2 x Be |
| I, II, III | Ae:=Aa+Ab |
If( Ba-Bb >= 0 ) then Be:=Ba-Bb; bt:=1 else Be:=Ba; bt:=0 |
|
| 17 | IV, V | If ( Bf[0] = 0 ) then Ab := -1 |
Ba:=Bf, Bb:=0 |
| I, II, III | Ae:=Aa+Ab |
Be:=Ba+Bb |
|
| 18 | IV, V | Af:=Ae |
If( Bf[0] = 0 ) then Bf:=2xBe else Bf:=Be |
Извлечение квадратного корня
Алгоритм извлечения квадратного корня является основной изюминкой Z3. В таблице 8 представлена микропоследовательность, состоящая из 20 циклов, необходимая для вычисления квадратного корня. Изначально аргумент операции хранится в паре регистров <Af,Bf>. Пара регистров <Aa,Ba> сброшена в 0. Алгоритм вычисляет квадратный корень числа с четной экспонентой. Если экспонента числа является не четной, то мантисса сдвигается на 1 разряд влево и экспонента декремируется. Итоговая экспонента (рассчитанная в цикле 19) равна половине исходной экспоненте.
Основная идея этого классического алгоритма заключается в сведении операции извлечения квадратного корня к операции деления. Для извлечения квадратного корня из x, нам потребуется ряд Q, таких что x/Q=Q. Итоговое Q получается последовательно установкой i-го разряда в 1 с последующей проверкой условия x > Q2. Если условие перестало выполняться, то i-ый разряд должен быть сброшен в 0.
Пусть мы уже вычислили результат с нулевого по -i+1 разряд. Обозначим через Q-i+1 мантиссу:
Q-i+1 = Bf[0] * 20 + Bf[-1] * 2-1 +… + Bf[-i+1] * 2-i+1
Далее разряд -i устанавливается в q-i, что должно сохранить условие:
x >= Q-i2 = ( Q-i+1 + q-i * 2-i )2
Это условие истинно, если:
x — Q-i2 = (x — Q-i+12) — 2-i q-i (2 Q-i+1 + 2-i q-i ) >= 0
Определим t-i с помощью выражения:
2-i * t-i = x Q-i2 = (x — Q-i+12) — 2-iq-i(2 Q-i+1 + 2-i q-i)
Это может быть записано как:
2-i t-i = t-i+1 2-i+1 — 2-i q-i ( 2 Q-i+1 + 2-i q-i )
в которой мы используем рекурсивное определение:
2-i+1 t-i+1 = ( x — Q2-i+1 )
Упростив предыдущее выражение мы получаем:
t-i = 2 t-i+1 — q-i (2 Q-i+1 + 2-i q-i)
Если t-i положительный для q-i = 1, то мы устанавливаем разряд -i итогового результата в 1, т.е. Bf[-i] := 1. Если же t-i отрицательный, то мы устанавливаем Bf[-i] := 0. Рекурсивные вычисления начинаются с t0 = x. Q-i+1 на каждом шаге представляет частичный результат, хранящийся в Bf. Разряд -i предварительно устанавливается в 1 и проверяется знак t-i. Основной цикл алгоритма извлечения квадратного корня для разряда -i имеет следующий вид:
Ba := 2 x Be
Bb := 2 x Bf
Bb[-i] := 1
if( Ba — Bb >= 0 ) then Be := Ba — Bb, Bf[-i] := 1
else Be := Ba, Bf[-i] := 0
Для вычисления квадратного корня используются все разряды регистра Bf. Если исходное число находится в заданном диапазоне, то результат тоже находится в заданном диапазоне.
Таблица 8. Циклы алгоритма извлечения квадратного корня
| Цикл | Стадия | Экспонента | Мантисса |
| 0 | I, II, III | ||
| 1 | IV, V | If( Af[0]=1 ) then Ba:=2 * Bf else Ba:=Bf Bb[0]:=1 |
|
| I, II, III | If( Ba-Bb >= 0 ) then Be:=Ba-Bb, bt:=1 else Be:=Ba, bt:=0 |
||
| 2 | IV, V | Bf:=0 if(bt=1) then Bb[0]:=1, Ba:=2*Be Bb:=2*Bf, Bb[-1]:=1 |
|
| I, II, III | If( Ba-Bb >= 0 ) then Be:=Ba-Bb, bt:=1 else Be:=Ba, bt:=0 |
||
| 3 | IV, V | if(bt=1) then Bb[-1]:=1, Ba:=2*Be Bb:=2*Bf, Bb[-2]:=1 |
|
| I, II, III | If( Ba-Bb >= 0 ) then Be:=Ba-Bb, bt:=1 else Be:=Ba, bt:=0 |
||
| ... | ... | ... | ... |
| i | IV, V | if(bt=1) then Bb[2-i]:=1, Ba:=2*Be Bb:=2*Bf, Bb[1-i]:=1 |
|
| I, II, III | If( Ba-Bb >= 0 ) then Be:=Ba-Bb, bt:=1 else Be:=Ba, bt:=0 |
||
| ... | ... | ... | ... |
| 18 | IV, V | if(bt=1) then Bb[-16]:=1, Ba:=2*Be Bb:=2*Bf |
|
| I, II, III | If( Ba-Bb >= 0 ) then Be:=Ba-Bb, bt:=1 else Be:=Ba, bt:=0 |
||
| 19 | IV, V | Aa:=Af / 2 |
Ba:=Bf, Bb:=0 |
| I, II, III | Ae:=Aa+0 |
Be:=Ba+Bb |
|
| 20 | IV, V | Af:=Ae |
Bf:=Be |
Инструкции Ввод с клавиатуры и Вывод результата
Две наиболее сложные инструкции Z3 c вводом и выводом в десятичной системе счисления. Десятичные числа из 4 цифр вводятся через клавиатуру и конвертируются в бинарное представление. Это осуществляется путем чтения каждой цифры последовательно, преобразования ее в двоичное представление и сохранения в разряды Ba[-10], Ba[-11], Ba[-12] и Ba[-13] регистра Ba. Число в регистре умножается на 10 и процедура повторяется с оставшимися цифрами. После 4 итераций десятичный ввод полностью преобразуется в двоичное представление (экспонента двоичного представления формируется косвенно через сдвиги при умножении на 10). Наиболее сложную часть составляет обработка экспоненты. Если экспонента e положительна, мантисса умножаться e раз на 10. Если отрицательная, то |e| раз на 0.1. Умножение на 10 относительно простое: мантисса в Be может быть сдвинута на 1 разряд влево и потом сохраниться в Ba (т.е. Ba := 2 x Be). В тоже время Be может быть сдвинута на 3 разряда влево и потом сохраниться в Bb (т.е. Bb := 8 x Be). Сложение Ba и Bb дает искомый результат: умножение числа из Be на 10. Процесс занимает 4 цикла для каждого умножения, итого 32 цикла для десятичной экспоненты +8. Так как операции чтения требуется минимум девять циклов, то это означает, что десятичное число с экспонентой +8 читается за 41 циклов.
В случае отрицательной экспоненты, умножение на константу 0.1 осуществляется так же с помощью сдвигов и сложения. Это умножение немного сложнее, т. к. число 0.1 в двоичном представлении периодично. Описание микропоследовательности увело бы нас слишком далеко от основной темы, так что мы ее опустим. (Ее можно найти в патентной заявке Цузе. [14]).
Инструкция отображения на дисплеи осуществляется с помощью итеративных умножений или делений на 10. Если бинарная экспонента в регистре R1 положительная, то число умножается на 0.1 столько раз, сколько требуется, что бы сделать двоичную экспоненту равной двум и пока 4 левых разряда регистра Bf содержат число от 0 до 9 (0000 и 1001). Это десятичное число, которое может быть отображено в следующей колонке панели вывода. Число вычитается из мантиссы в Bf и процесс продолжается со следующей цифрой. Если бинарная экспонента в R1 отрицательная, то процесс схож, за тем исключением, что осуществляется умножение на 10.
Общая архитектура Z3
Теперь рассмотрим детальную диаграмму Z3, изображенную на рис. 8. Устройств управления и панели ввода/вывода были рассмотрены ранее. Заметим, что 4 десятичные цифры клавиатуры ввода перемещаются в регистр Ba через блоки переключателей Za, Zb, Zc и Zd, которые активируются друг за другом.
Блоки переключателей Eg и Ei используются для загрузки некоторых используемых констант в регистры экспоненты (+13 и -4, которые используются для преобразования системы счисления). Сдвигающее устройство Ee между регистром Af и регистром Aa используется в алгоритме извлечения квадратного корня. Экспонента результата (Aa) становится равной половине экспоненты исходного числа (Af).
Ah1 является переключателем с двумя состояниями. Когда он в нуле, пара регистров <Af,Bf> доступна для загрузки операндов. Этот переключатель сбрасывается в нуль управляющей линией ai. Управляющие линии al, aj, bl и bj используются для очистки регистра Af, Ab, Bf и Bb при необходимости.
Блок названный «нуль, бесконечность» под Ae представляет собой схемы обработки исключений. Они непрерывно отслеживают шину данных (результаты операций и данных из памяти) и при необходимости устанавливают соответствующие флаги исключений. Сдвигающее устройство под Be используется для сдвига мантиссы на один разряд вправо. Это нужно для нормализации, в случаях когда Be >= 2.
Переключатели Fp и Fq управляют количеством и направлением сдвига в сдвигающем устройстве под блоками переключателей Fc и Fa. Переключатели Fh, Fi, Fk, Fl и Fm выполняют схожую функцию на другом сдвигающем устройстве. Эти 5 разрядов представляют число от -16 до 15, что соответствует диапазону второго сдвигающего устройства. После осуществления сдвига, число представляемое переключателями с Fh по Fm перемещается через блок переключателей Bn в регистр Ab в соответствии с алгоритмом изменения экспоненты результата. Если число сдвигается на 10 разрядов влево, то +10 вычитается из экспоненты результата. Такие большие сдвиги нужны, в основном, после вычислений.
Взглянем снова на схему машины Z3. Все в этой машине похоже на современный микропроцессор с плавающей точкой. Поразительно, как Цузе смог найти столь хорошее архитектурное решение на самой заре вычислительных машин. Процессор Z3 включает всего 600 реле; на память уходит в три раза больше. С целью оптимизировать структуру без возможности изменить аппаратное обеспечение Цузе был вынужден все время переосмысливать логическую структуру машины. Ему была не доступна такая роскошь, как неограниченное финансирование выделяемое министерством обороны США на разработку ENIAC или корпорацией IBM на Mark I. Он был один. Не смотря на то, что это давало ему преимущество на концептуальной стороне, это так же приносило свои минусы, учитывая сколь низкое влияние оказывали машины Z1 и Z3 на зарождающуюся в США компьютерную отрасль после Второй мировой войны. [13]

Изобретение компьютера
Основным недостатком Z3 является полное отсутствие условных переходов во множестве инструкций. Когда программа хранится на перфоленте, возможным путем решения этой проблемы является введение нескольких лент и механизма, позволяющего переключаться между лентами (как было с делано в Гарвардской Mark I). Другим путем является использование программного счетчика, чтобы перфолента могла быть перемотана вперед и назад по требованию.
Иногда грань между Вычислительными машинами и Универсальными компьютерами проводится на основе способа хранения программ (внешнего и внутреннего). Я считаю, что этот критерий не является подходящим. Внешняя программа может работать как интерпретатор числовых данных. Внешняя программа становится постоянной частью процессора, а данные становятся программами, таким же образом, каким Универсальная машина Тьюринга работает как интерпретатор. Я считаю, что необходимым условием Универсального компьютера является минимальный набор инструкций и косвенная адресация.[11] Косвенная адресация может симулироваться написанием само-модифицируемой программы, таким образом набор инструкций становится определяющим критерием. Машина с достаточным количеством адресуемой памяти, аккумулятором и способная исполнять инструкции CLR(очистить), INC(инкремент), LOAD, STORE и BZ(ветвление, если нуль) является Универсальным компьютером. В этом случае, машина Z1 не была полноценным компьютером, но такими же было и множество других ранних компьютеров. Машина ABC являлась специализированной машиной, для решения систем линейных уравнений методом Гаусса. Гарвардский Mark I не обладал условным переходом, хотя реализовывал циклы. ENIAC не была программируемой — потоки данных между строительными блоками задавались аппаратно. Условные переходы были доступны с ограничениями, а о само-модифицируемых программах, само собой, и речи быть не могло.
Таблица 9. Сравнение архитектурных особенностей
| Машина | Память и ЦП разделены | Условные переходы | Программно или аппаратно программируемые | Самомодифицируемые программы | Косвенная адресация |
| Z1 | да | нет | soft | нет | нет |
| Машина Атанасова | да | нет | hard | нет | нет |
| Гарвардский Mark I | нет | нет | soft | нет | нет |
| ENIAC | нет | частично | hard | нет | нет |
| Мачестерский Mark I | да | да | soft | нет | нет |
Таблица 10. Некоторые дополнительные архитектурные особенности
| Машина | Внутренняя система счисления | С постоянной или плавающей запятой | Поразрядная арифметика | Архитектура | Технология |
| Z1 | двоичная | плавающей | нет | последовательная | механическая |
| Машина Атанасова | двоичная | постоянная | да | векторная | электронная |
| Гарвардский Mark I | десятичная | постоянной | нет | параллельная | электромеханическая |
| ENIAC | десятичная | постоянной | нет | поток данный | электронная |
| Мачестерский Mark I | двоичная | постоянной | да | последовательная | электронная |
Таблицы 9 и 10 демонстрируют наиболее значимую информацию о ранних вычислительных машинах, упоминаемых выше. Как должно быть ясно из таблиц, ни одна из ранних вычислительных машин не удовлетворяла всем условиям Универсального компьютера. Я так же упомянул Манчестерский Mark I, строившийся с 1946 по 1948 потому, что, насколько я знаю, это первая машина, полностью соответствующая моим условиям Универсального компьютера. Машина Mark I строилась под руководством Фредерика Уильямса( F.C. Williams ) и Тома Килберна (T. Kilburn). Она хранит свою программу в памяти с произвольным доступом реализованной на электронно-лучевой трубке. Все необходимые элементарные инструкции доступны (в модифицированной форме), и несмотря на то, что в ней отсутствует косвенная адресация, в ней может быть реализованы само-модифицируемые программы. Первая программа была запущена в июне 1948, которая рассчитывала наибольший собственный делитель большого числа. В сентябре 1948, Тьюринг получил звание Reader в математическом департаменте Манчестерского университета и написал несколько программ для первого универсального компьютера в мире. Его видение универсального компьютера было опубликовано в 1936, в тот же год, когда было завершено запоминающее устройство Z1. Таблицы 9 и 10 выражают, что изобретение компьютера было коллективным достижением и охватывает 12 лет.
Благодарности
Расшифровка схематической документации была возможна только в сотрудничестве с некоторыми из в моих студентов в университетах в Галле и Берлине. Я благодарю Александра Турма (Alexander Thurm) и Алекса Бауера (Axel Bauer), реализовавших gata-level симулятор процессора Z3. Мы поняли, что такое проблема синхронизации, когда симулятор отказывался запускаться. Так же благодарю Франца Конечного (Franz Konieczny), Реймунда Шпитцера (Reimund Spitzer) и Роланда Шультса (Roland Schultes), написавших часть stand-alone симулятора процессора. Мы начали работать на Z3 с помощью Конрада Цузе, охотно отвечающего на наши вопросы. Мы были поражены, как после более чем 60 лет, вся конструкция Z3 сохраняется у него в голове. С сожалению, Цузе умер в декабре 1995, до того как описание его работы было завершено. Эта работа посвящена его памяти.
Литература
- H. Aiken and G. Hopper, “The Automatic Sequence Controlled Calculator,” reprinted in B. Randell, ed., The Origins of Digital Computers. Berlin: Springer Verlag, 1982, pp. 203-222.
- A.W. Burks and A.R. Burks, “The ENIAC: First General Purpose Electronic Computer,” Annals of the History of Computing, vol. 3, no. 4, pp. 310-399, 1981.
- A.W. Burks and A.R. Burks, The First Electronic Computer: The Atanasoff Story. Ann Arbor: Univ. of Michigan Press, 1988.
- K.-H. Czauderna, Konrad Zuse, der Weg zu seinem Computer Z3. Munich: Oldenbourg Verlag, 1979.
- D. Knuth, The Art of Computer Programming-Seminumerical Algorithms, vol. 2. Reading, Mass.: Addison Wesley, 1981.
- I. Koren, Computer Arithmetic Algorithms. Englewood Cliffs, N.J.: Prentice Hall, 1993.
- S.H. Lavington, A History of Manchester Computers. Manchester, England: NCC Publications, 1975.
- S.H. Lavington, Early British Computers. Manchester, England: Digital Press, 1980.
- B. Randell, ed., The Origins of Digital Computers. Berlin: Springer Verlag, 1982.
- R. Rojas, “Who Invented the Computer? The Debate from the Viewpoint of Computer Architecture,” W. Gautschi, ed., Fifty Years Mathematics of Computation, Proceedings of Symposia in Applied Mathematics, AMS, pp. 361-366, 1993.
- R. Rojas, “On Basic Concepts of Early Computers in Relation to Contemporary Computer Architectures,” Proc. 13th World Computer Congress, Hamburg, pp. 324-331, 1994.
- U. Schweier and D. Saupe, “Funktions und Konstruktions prinzipien der programmgesteuerten mechanischen Rechen maschine Z1,” Arbeitspapiere der GMD 321, Bonn, 1988.
- N. Stern, From ENIAC to UNIVAC. Bedford: Digital Press, 1981.
- K. Zuse, Patentanmeldung Z-2391, German Patent Office, Berlin, 1941.
- K. Zuse, Der Computer mein Lebenswerk. Berlin: Springer-Verlag, 1970.
- K. Zuse, personal communication, Mar. 18, 1995.