Речь сегодня пойдёт о генерации изображений с картой расстояний (Signed Distance Field). Данный вид изображений примечателен тем, что фактически позволяет получить «векторную» графику на видеоускорителе, причём даром. Одной из первых данный метод растеризации предложила компания Valve в игре Team Fortress 2 для масштабируемых декалей в 2007 году, но до сих пор он не пользуется особой популярностью, хотя позволяет рендерить прекрасного качества шрифты, используя текстуру всего 256х256 точек. Данный метод прекрасно подходит для современных экранов высокой чёткости и позволяет серьёзно сэкономить на текстурах в играх, он не требователен к железу и прекрасно работает на смартфонах.

Хитрость заключается в создании такой специально подготовленной карты расстояний, что при использовании простейшего шейдера получается идеальная векторная картинка. Более того, с помощью шейдеров можно получить эффекты тени, свечения, объёма и т. п.
Как же создавать такие изображения? Очень просто, ImageMagick позволяет сделать это одной командой:
На этом можно было бы поставить точку, но так полноценного топика не получится. Что ж, под катом — описание быстрого алгоритма расчёта SDF, пример на C++ и немного шейдеров для OpenGL.
Первая команда в начале данного поста — это рецепт генерации SDF из любого черно-белого растрового контура. Он основан на новой возможности ImageMagick: морфологии. Среди морфологических преобразований присутствует и вычисление карты расстояний.
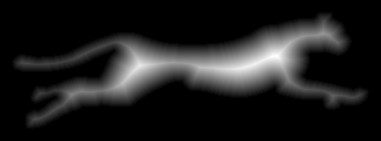
Расчёт карты расстояний — простейший алгоритм. Он работает на монохромных изображениях, где пиксель либо чёрный, либо белый. Один из цветов считаем внутренним, другой — внешним (как больше нравится, на этой картинке с гепардом чёрный пиксель будет внутренним). Иногда их называют цветами фона и переднего плана. Для каждого «внутреннего» пикселя изображения нужно найти ближайший к нему «внешний» пиксель и установить значение яркости этого пикселя как евклидово расстояние до ближайшего «внешнего» пикселя. То есть нужно вычислить расстояния до всех «внешних» пикселей изображения и выбрать наименьшее из них. Получившаяся карта расстояний называется Distance Field (DF), но она пока нам не подходит. Чтобы получить SDF (Signed DF), инвертируем изображение, повторяем алгоритм, снова инвертируем и складываем с предыдущим результатом.
Значение интенсивности не обязательно устанавливать точно в значение расстояния: можно масштабировать «расплывчатость» изображения в зависимости от потребностей. В частности, для рендеринга чётких контуров лучше использовать менее размытую карту, а для таких спецэффектов как тень или свечение — лучше увеличить карту расстояний:

И хотя ImageMagick не самый быстрый и простой способ сделать подобную карту, я думаю это лучший вариант, так как ImageMagick присутствует практически на всех операционных системах и нередко используется разработчиками для конвейерной обработки спрайтов. Достаточно немного доделать скрипт и поставить генерацию изображений на поток.
Рассмотрим, как это работает. Если просто взять и применить операцию morphology к нашему изображению, получим не лучший результат:

Малевич? Нет, простонегры ночью воруют уголь не хватает контрастности, её можно быстро вытянуть параметром

Сразу бросается в глаза недостаток: карта расстояний генерируется только снаружи. Это следствие того, что сам алгоритм тоже двухпроходный, повторим то же самое для негатива:
Теперь обратная ситуация — не хватает карты снаружи.
Осталось объединить эти два алгоритма, используя промежуточный слой, докрутить контрастность и получаем зубодробительный скрипт из начала поста:
Некоторые пояснения:
Хорошо, если есть оригинал более высокого разрешения — тогда можно обойтись без трюка с увеличением масштаба и масштабировать уже только в меньшую сторону:
Обратите внимание, что фильтр Jinc «переехал» в конец цепочки, так как призван улучшить качество сэмплирования при уменьшении размера карты. Также не стоит убирать
Некоторые спорные вопросы.
Есть ли смысл «вытягивать» контраст? Вообще теоретически при увеличении контраста увеличивается дельта семплов, из которых потом аппаратным методом интерполяции рассчитывается антиалиасинг. Если коротко — вытягивать нужно, особенно если планируется выводить чёткие сглаженные контуры и не так важны эффекты вроде теней. Если исходная карта будет не только растягиваться, но и сжиматься, сильно увлекаться не стоит — в противном случае при уменьшении картинки будет портиться антиалиасинг, достигаемый за счёт размытых краёв SDF.
Как качество зависит от разрешения SDF-карты? Я постарался построить график зависимости PSNR от разрешения карты и контрастности. В целом качество увеличивается, но ещё сильно зависит от контрастности карты. Оценить зависимости можно на графике:
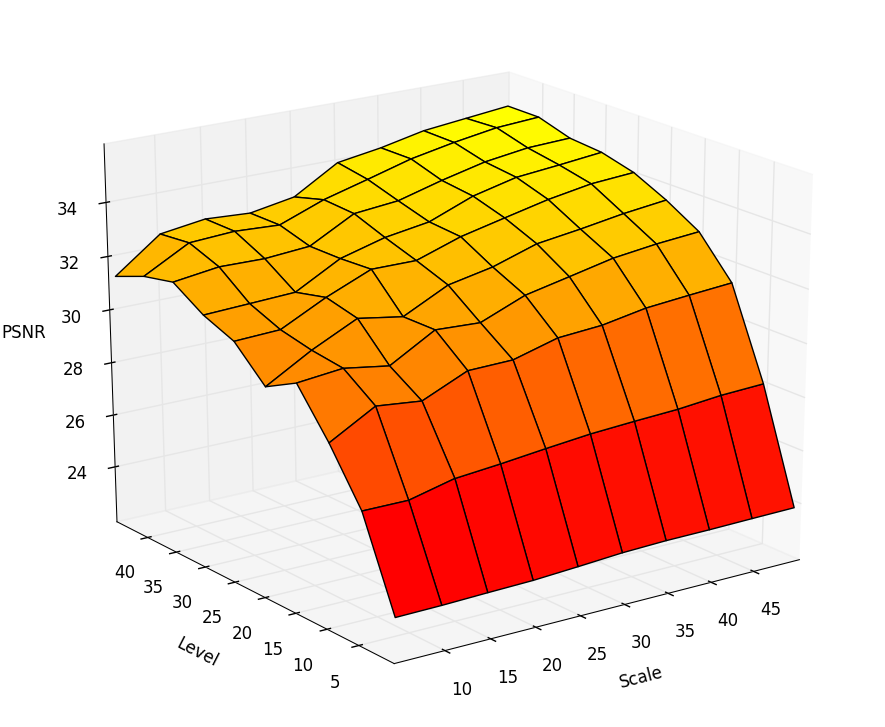
Здесь Scale — это масштаб в процентах от исходника, Level — насколько сильно был «вытянут» контраст. Можно сделать вывод, что от масштаба зависимость не очень уж и линейная, 30% будет весьма компромиссным вариантом, а контрастность довольно сильно влияет на качество контура.
Насколько сильно влияет на качество размер фильтра Euclidean? Увеличение размера фильтра даёт прирост в 0,1 дБ +- копейки, на мой взгляд это несущественно.
Насколько сильно можно «ужать» исходное изображение? Это сильно зависит от формы. SDF не любит острые углы, а такая плавная картинка как гепард из примера превосходно чувствует себя даже в миниатюрном масштабе:

Алгоритм прост, но его реализация «в лоб» будет работать часами: по сути нужно для каждого пикселя просканировать всё изображение. O(N^2) нас совершенно не устраивает. Но умные люди уже подумали и придумали алгоритм точного (!) расчёта DF, который работает за O(N). Осталось распространить задачу до SDF, что довольно просто (см. предыдущий пример).
Суть. Вместо того чтобы считать для каждого пикселя расстояние, выполним два последовательных прохода по изображению, просто инкрементируя расстояние при определённых условиях. Это напоминает алгоритм быстрого Box-размывания изображения. Матан можно почерпнуть из [2], я же постараюсь объяснить на пальцах.
Пикселем p я буду называть элемент массива N*M, составленный из исходного изображения. Пиксель — это следующая структура:
Как видно, здесь ничего нет о яркости и т.п. — оно и не нужно. Массив формируется так:
Если пиксель исходного изображения светлый, то
Если пиксель исходного изображения тёмный, то
У каждого пикселя есть 8 соседей, пронумеруем их таким образом:
Далее введём две вспомогательные функции. Функция h нужна для вычисления расстояния Евклида между пикселем и соседом, функция G — для вычисления нового значения расстояния по компонентам.
Первый проход. Данный проход выполняется в прямом порядке (от левого верхнего угла изображения к правому нижнему). Псевдокод:
Второй проход. Данный проход выполняется в обратном порядке (от правого нижнего угла изображения к левому верхнему). Псевдокод:
Алгоритм нужно повторить для негатива исходного изображения. Потом для двух полученных карт нужно произвести окончательное вычисление расстояния и вычитание для объединения двух карт DF в одну SDF:
Изначально в структуре мы хранили квадрат Евклидова расстояния, поэтому нужно извелчь корень. Зачем нужно прибавить единицу — не спрашивайте, результат эмпирический и без него получается криво:) Финальная карта SDF — результат вычитания второй из первой, далее нужно отмасштабировать значение как нравится.
На мой взгляд даже попытка на пальцах объяснить, как это работает, выглядит очень запутанной, поэтому я приведу исходный код на C++. В качестве входного изображения я использовал QImage из Qt, чтобы не портить наглядность процесса. Исходник основан на источнике [3], но там есть баги.
Здесь используется хитрость: так как оба прохода используют «окно» шириной в 1 пиксель, я добавляю однопиксельный бордюр вкоруг исходного изображения, чтобы избежать проверки границ. Для негатива бордюр тоже нужно изменить на противоположное значение, чего не было учтено в [3].
Полноценный рабочий алгоритм можно посмотреть в генераторе растровых шрифтов с открытым исходным кодом UBFG. Пример результата:

Идея обратного преобразования (из SDF в растровый контур) основана на увеличении контрастности до такой степени, что «размытые» края не будут видны. Изменяя контрастность SDF можно получить различные эффекты, а также регулировать качество антиалиасинга изображения. В качестве примера возьмём исходник:

Это тоже SDF, просто сильно сжатый и уменьшенный в размере. Увеличим его в 16 раз:
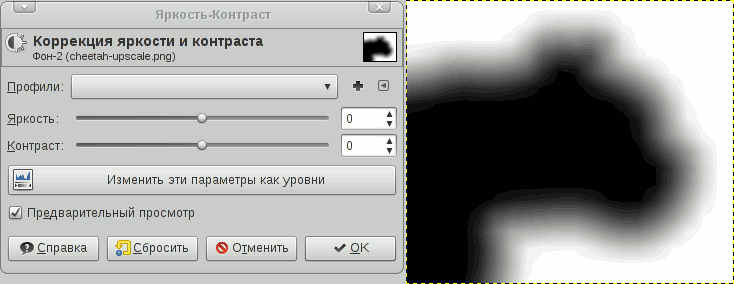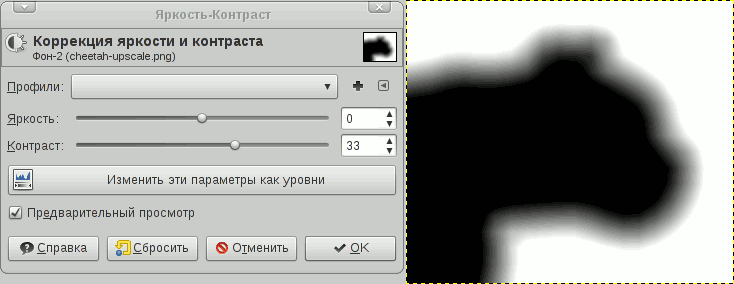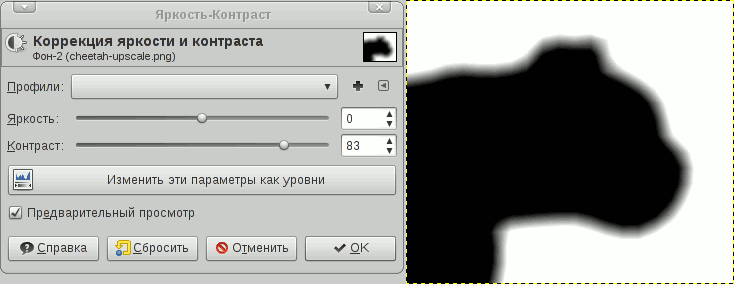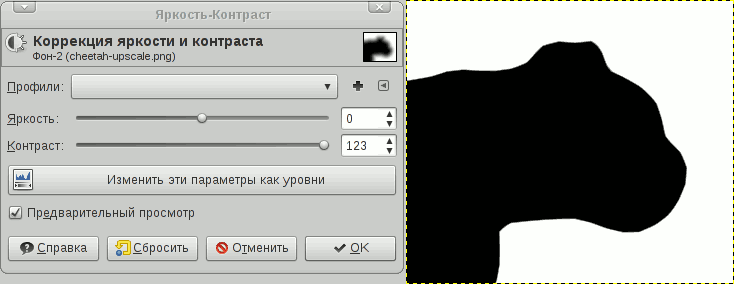
Теперь, чтобы получить красивый контур, увеличим контрастность. Я для этих целей использовал GIMP:
Чтобы увидеть результат использования SDF в реальном времени, без шейдеров не обойтись. Простейший альфа-тест также может применяться, но он рубит на корню антиалиасинг. Однако используемый шейдер представляет собой всего пару инструкций и фактически не влияет на производительность. Более того, учитывая что шейдеры сейчас дешёвые, а память/кэш дорогие — можно получить неплохое ускорение за счёт экономии видеопамяти.
Теперь посмотрим, как это дело можно использовать в OpenGL. Все примеры будут даны в виде чистого GLSL исходного кода. Опробовать можно в любом шейдерном редакторе. Все примеры я тестировал в редакторе Kick.js, поскольку это единственный редактор, который позволяет загрузить свои текстуры.
Здесь просто вытягиваем контраст относительно среднего значения (0.5). Сила контраста должна варьироваться в зависимости от масштаба текстуры и размазанности карты DF — параметр подбирается экспериментально и задаётся через uniform с множителем масштаба.
Немного улучшить качество можно фильтром
Здесь порог также нужно подобрать.
Чтобы получить такой эффект, нужно взять два порога и инвертировать цвет:
Результат:

Чуть похимичить над предыдущим примером — и получаем эффект свечения:
Чтобы получилась тень, нужно взять цвет для glow со смещением:
Результат:

Результат может показаться не ахти, но это потому что я использовал слишком маленькую карту:

[1] Improved Alpha-Tested Magnification for Vector Textures and Special Effects — та самая статья от Valve.
[2] Frank Y. Shih, Yi-Ta Wu. Fast Euclidean distance transformation in two scans using a 3x3 neighborhood — китайцы? Нет, всего лишь университет Нью Джерси.
[3] www.codersnotes.com/notes/signed-distance-fields — тут тоже довольно быстрый алгоритм, но к сожалению его автор допустил несколько ошибок и присутствует умножение, что чуть медленнее алгоритма, представленного в этой статье.
[4] contourtextures.wikidot.com — ещё одна реализация расчёта SDF, но её преимущество в том, что может учитывать сглаживание краёв для определения ближайших точек. Насчёт производительности ничего не говорится, но хорош, когда нет возможности получить оригинал высокого разрешения (с другой стороны можно просто обойтись трюком с upscale). Если был опыт использования — отписывайтесь в комментариях.
[5] gpuhacks.wordpress.com/2013/07/08/signed-distance-field-rendering-of-color-bit-planes — метод рендеринга цветных векторных изображений (подходит для небольшого количества цветов).
[6] distance.sourceforge.net — интересный ресурс, на котором сравниваются различные алгоритмы подсчёта SDF.
upd. Спасибо замечанию Bas1l, алгоритм всё-таки не совсем точный и может давать ошибки на вычислении расстояния до ближайших соседей из-за ошибки в доказательстве. В этой статье представлена улучшенная версия алгоритма.
upd2. От пользователя achkasov замечание по части шейдеров. В случае резких переходов на SDF карте могут появляться заплывы и неравномерный антиалиасинг. Подробнее об эффекте и о том, как с этим бороться: iquilezles.org/www/articles/distance/distance.htm
Изменив шейдр, получаем значительное улучшение в области, кхм, хвоста:


Хитрость заключается в создании такой специально подготовленной карты расстояний, что при использовании простейшего шейдера получается идеальная векторная картинка. Более того, с помощью шейдеров можно получить эффекты тени, свечения, объёма и т. п.
Как же создавать такие изображения? Очень просто, ImageMagick позволяет сделать это одной командой:
convert in.png -filter Jinc -resize 400% -threshold 30% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -resize 25% out.png
На этом можно было бы поставить точку, но так полноценного топика не получится. Что ж, под катом — описание быстрого алгоритма расчёта SDF, пример на C++ и немного шейдеров для OpenGL.
Что это было за заклинание?
Первая команда в начале данного поста — это рецепт генерации SDF из любого черно-белого растрового контура. Он основан на новой возможности ImageMagick: морфологии. Среди морфологических преобразований присутствует и вычисление карты расстояний.
Расчёт карты расстояний — простейший алгоритм. Он работает на монохромных изображениях, где пиксель либо чёрный, либо белый. Один из цветов считаем внутренним, другой — внешним (как больше нравится, на этой картинке с гепардом чёрный пиксель будет внутренним). Иногда их называют цветами фона и переднего плана. Для каждого «внутреннего» пикселя изображения нужно найти ближайший к нему «внешний» пиксель и установить значение яркости этого пикселя как евклидово расстояние до ближайшего «внешнего» пикселя. То есть нужно вычислить расстояния до всех «внешних» пикселей изображения и выбрать наименьшее из них. Получившаяся карта расстояний называется Distance Field (DF), но она пока нам не подходит. Чтобы получить SDF (Signed DF), инвертируем изображение, повторяем алгоритм, снова инвертируем и складываем с предыдущим результатом.
Значение интенсивности не обязательно устанавливать точно в значение расстояния: можно масштабировать «расплывчатость» изображения в зависимости от потребностей. В частности, для рендеринга чётких контуров лучше использовать менее размытую карту, а для таких спецэффектов как тень или свечение — лучше увеличить карту расстояний:

И хотя ImageMagick не самый быстрый и простой способ сделать подобную карту, я думаю это лучший вариант, так как ImageMagick присутствует практически на всех операционных системах и нередко используется разработчиками для конвейерной обработки спрайтов. Достаточно немного доделать скрипт и поставить генерацию изображений на поток.
Рассмотрим, как это работает. Если просто взять и применить операцию morphology к нашему изображению, получим не лучший результат:
convert nosdf.png -morphology Distance Euclidean sdf.png

Малевич? Нет, просто
-auto-level:convert nosdf.png -morphology Distance Euclidean -auto-level sdf.png

Сразу бросается в глаза недостаток: карта расстояний генерируется только снаружи. Это следствие того, что сам алгоритм тоже двухпроходный, повторим то же самое для негатива:
convert nosdf.png -negate -morphology Distance Euclidean -auto-level sdf.png

Теперь обратная ситуация — не хватает карты снаружи.
Осталось объединить эти два алгоритма, используя промежуточный слой, докрутить контрастность и получаем зубодробительный скрипт из начала поста:
convert in.png -filter Jinc -resize 400% -threshold 30% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -resize 25% out.png
Некоторые пояснения:
-resize 400% — увеличиваем исходное изображение, чтобы устранить зубчатые края. Алгоритм работает только для черно-белых изображений и хотелось бы хоть как-то учитывать антиалиасинг. Но я бы порекомендовал всегда иметь под рукой оригинал четырёхкратного размера или больше. Valve, например, для демонстрации использует 4K изображение, из которого получает SDF размером 64x64. Это конечно уже перебор. Я нахожу приемлемым соотношение 8:1.-level 45%,55% — можно регулировать степень размывания карты расстояний, по умолчанию она уж очень расплывчатая.-filter Jinc и -threshold 30% — экспериментально, данный фильтр и порог обеспечивает наилучшее соответствие исходному изображению. Под спойлером скрипт и исходник для желающих проверить.Скрипт для поиска наилучшей метрики PSNR
Естественно, единственно верного варианта быть не может, но я оставил Jinc 30% как наиболее средний вариант, дающий приемлемый результат.
Изображение:

Скрипт:
Изображение:

Скрипт:
#!/bin/sh
convert orig.png -resize 25% .orig-downscaled.png
convert orig.png -threshold 50% .orig-threshold.png
SIZE=$(identify orig.png| cut -d' ' -f3)
MAX=0.0
MAXRES=""
for filter in $(convert -list filter)
do
for threshold in $(seq 1 99)
do
convert .orig-downscaled.png -filter $filter -resize $SIZE! -threshold $threshold% .tmp.png
PSNR=$(compare -metric PSNR .orig-threshold.png .tmp.png /dev/null 2>&1)
if [ "$(echo "$MAX < $PSNR" | bc -l)" = "1" ]
then
MAXRES="$PSNR $filter $threshold"
echo $MAXRES
MAX=$PSNR
fi
rm .tmp.png
done
done
rm .orig-threshold.png .orig-downscaled.png
Хорошо, если есть оригинал более высокого разрешения — тогда можно обойтись без трюка с увеличением масштаба и масштабировать уже только в меньшую сторону:
convert in.png -threshold 50% \( +clone -negate -morphology Distance Euclidean -level 50%,-50% \) -morphology Distance Euclidean -compose Plus -composite -level 45%,55% -filter Jinc -resize 10% out.png
Обратите внимание, что фильтр Jinc «переехал» в конец цепочки, так как призван улучшить качество сэмплирования при уменьшении размера карты. Также не стоит убирать
-threshold 50% — Euclidean некорректно работает для не-монохромных изображений.Некоторые спорные вопросы.
Есть ли смысл «вытягивать» контраст? Вообще теоретически при увеличении контраста увеличивается дельта семплов, из которых потом аппаратным методом интерполяции рассчитывается антиалиасинг. Если коротко — вытягивать нужно, особенно если планируется выводить чёткие сглаженные контуры и не так важны эффекты вроде теней. Если исходная карта будет не только растягиваться, но и сжиматься, сильно увлекаться не стоит — в противном случае при уменьшении картинки будет портиться антиалиасинг, достигаемый за счёт размытых краёв SDF.
Как качество зависит от разрешения SDF-карты? Я постарался построить график зависимости PSNR от разрешения карты и контрастности. В целом качество увеличивается, но ещё сильно зависит от контрастности карты. Оценить зависимости можно на графике:

Здесь Scale — это масштаб в процентах от исходника, Level — насколько сильно был «вытянут» контраст. Можно сделать вывод, что от масштаба зависимость не очень уж и линейная, 30% будет весьма компромиссным вариантом, а контрастность довольно сильно влияет на качество контура.
Насколько сильно влияет на качество размер фильтра Euclidean? Увеличение размера фильтра даёт прирост в 0,1 дБ +- копейки, на мой взгляд это несущественно.
Насколько сильно можно «ужать» исходное изображение? Это сильно зависит от формы. SDF не любит острые углы, а такая плавная картинка как гепард из примера превосходно чувствует себя даже в миниатюрном масштабе:
Реализация быстрого алгоритма на C++
Алгоритм прост, но его реализация «в лоб» будет работать часами: по сути нужно для каждого пикселя просканировать всё изображение. O(N^2) нас совершенно не устраивает. Но умные люди уже подумали и придумали алгоритм точного (!) расчёта DF, который работает за O(N). Осталось распространить задачу до SDF, что довольно просто (см. предыдущий пример).
Суть. Вместо того чтобы считать для каждого пикселя расстояние, выполним два последовательных прохода по изображению, просто инкрементируя расстояние при определённых условиях. Это напоминает алгоритм быстрого Box-размывания изображения. Матан можно почерпнуть из [2], я же постараюсь объяснить на пальцах.
Пикселем p я буду называть элемент массива N*M, составленный из исходного изображения. Пиксель — это следующая структура:
{
x, y - это покоординатное расстояние
f - квадрат Евклидова расстояния
}
Как видно, здесь ничего нет о яркости и т.п. — оно и не нужно. Массив формируется так:
Если пиксель исходного изображения светлый, то
x = y = 9999
f = 9999 * 9999
Если пиксель исходного изображения тёмный, то
x = y = f = 0
У каждого пикселя есть 8 соседей, пронумеруем их таким образом:
2 3 4
1 p 5
8 7 6
Далее введём две вспомогательные функции. Функция h нужна для вычисления расстояния Евклида между пикселем и соседом, функция G — для вычисления нового значения расстояния по компонентам.
h(p, q) {
if q - сосед 1 или 5 {return 2 * q.x + 1}
if q - сосед 3 или 7 {return 2 * q.y + 1}
в остальных случаях {return 2 * (q.x + q.y + 1)}
}
G(p, q) {
if q - сосед 1 или 5 {return (1, 0)}
if q - сосед 3 или 7 {return (0, 1)}
в остальных случаях {return (1, 1)}
}
Первый проход. Данный проход выполняется в прямом порядке (от левого верхнего угла изображения к правому нижнему). Псевдокод:
для каждого пикселя p изображения {
для каждого соседа q от 1 до 4 {
if (h(p, q) + q.f < p.f) {
p.f = h(p, q) + q.f
(p.x, p.y) = (q.x + q.y) + G(p, q)
}
}
}
Второй проход. Данный проход выполняется в обратном порядке (от правого нижнего угла изображения к левому верхнему). Псевдокод:
для каждого пикселя p изображения {
для каждого соседа q от 5 до 8 {
if (h(p, q) + q.f < p.f) {
p.f = h(p, q) + q.f
(p.x, p.y) = (q.x + q.y) + G(p, q)
}
}
}
Алгоритм нужно повторить для негатива исходного изображения. Потом для двух полученных карт нужно произвести окончательное вычисление расстояния и вычитание для объединения двух карт DF в одну SDF:
d1 = sqrt(p1.f + 1);
d2 = sqrt(p2.f + 1);
d = d1 - d2;
Изначально в структуре мы хранили квадрат Евклидова расстояния, поэтому нужно извелчь корень. Зачем нужно прибавить единицу — не спрашивайте, результат эмпирический и без него получается криво:) Финальная карта SDF — результат вычитания второй из первой, далее нужно отмасштабировать значение как нравится.
На мой взгляд даже попытка на пальцах объяснить, как это работает, выглядит очень запутанной, поэтому я приведу исходный код на C++. В качестве входного изображения я использовал QImage из Qt, чтобы не портить наглядность процесса. Исходник основан на источнике [3], но там есть баги.
Исходник
#include <QPainter>
#include <stdio.h>
#include <math.h>
struct Point
{
short dx, dy;
int f;
};
struct Grid
{
int w, h;
Point *grid;
};
Point pointInside = { 0, 0, 0 };
Point pointEmpty = { 9999, 9999, 9999*9999 };
Grid grid[2];
static inline Point Get(Grid &g, int x, int y)
{
return g.grid[y * (g.w + 2) + x];
}
static inline void Put(Grid &g, int x, int y, const Point &p)
{
g.grid[y * (g.w + 2) + x] = p;
}
static inline void Compare(Grid &g, Point &p, int x, int y, int offsetx, int offsety)
{
int add;
Point other = Get(g, x + offsetx, y + offsety);
if(offsety == 0) {
add = 2 * other.dx + 1;
}
else if(offsetx == 0) {
add = 2 * other.dy + 1;
}
else {
add = 2 * (other.dy + other.dx + 1);
}
other.f += add;
if (other.f < p.f)
{
p.f = other.f;
if(offsety == 0) {
p.dx = other.dx + 1;
p.dy = other.dy;
}
else if(offsetx == 0) {
p.dy = other.dy + 1;
p.dx = other.dx;
}
else {
p.dy = other.dy + 1;
p.dx = other.dx + 1;
}
}
}
static void GenerateSDF(Grid &g)
{
for (int y = 1; y <= g.h; y++)
{
for (int x = 1; x <= g.w; x++)
{
Point p = Get(g, x, y);
Compare(g, p, x, y, -1, 0);
Compare(g, p, x, y, 0, -1);
Compare(g, p, x, y, -1, -1);
Compare(g, p, x, y, 1, -1);
Put(g, x, y, p);
}
}
for(int y = g.h; y > 0; y--)
{
for(int x = g.w; x > 0; x--)
{
Point p = Get(g, x, y);
Compare(g, p, x, y, 1, 0);
Compare(g, p, x, y, 0, 1);
Compare(g, p, x, y, -1, 1);
Compare(g, p, x, y, 1, 1);
Put(g, x, y, p);
}
}
}
static void dfcalculate(QImage *img, int distanceFieldScale)
{
int x, y;
int w = img->width(), h = img->height();
grid[0].w = grid[1].w = w;
grid[0].h = grid[1].h = h;
grid[0].grid = (Point*)malloc(sizeof(Point) * (w + 2) * (h + 2));
grid[1].grid = (Point*)malloc(sizeof(Point) * (w + 2) * (h + 2));
/* create 1-pixel gap */
for(x = 0; x < w + 2; x++)
{
Put(grid[0], x, 0, pointInside);
Put(grid[1], x, 0, pointEmpty);
}
for(y = 1; y <= h; y++)
{
Put(grid[0], 0, y, pointInside);
Put(grid[1], 0, y, pointEmpty);
for(x = 1; x <= w; x++)
{
if(qGreen(img->pixel(x - 1, y - 1)) > 128)
{
Put(grid[0], x, y, pointEmpty);
Put(grid[1], x, y, pointInside);
}
else
{
Put(grid[0], x, y, pointInside);
Put(grid[1], x, y, pointEmpty);
}
}
Put(grid[0], w + 1, y, pointInside);
Put(grid[1], w + 1, y, pointEmpty);
}
for(x = 0; x < w + 2; x++)
{
Put(grid[0], x, h + 1, pointInside);
Put(grid[1], x, h + 1, pointEmpty);
}
GenerateSDF(grid[0]);
GenerateSDF(grid[1]);
for(y = 1; y <= h; y++)
for(x = 1; x <= w; x++)
{
double dist1 = sqrt((double)(Get(grid[0], x, y).f + 1));
double dist2 = sqrt((double)(Get(grid[1], x, y).f + 1));
double dist = dist1 - dist2;
// Clamp and scale
int c = dist * 64 / distanceFieldScale + 128;
if(c < 0) c = 0;
if(c > 255) c = 255;
img->setPixel(x - 1, y - 1, qRgb(c,c,c));
}
free(grid[0].grid);
free(grid[1].grid);
}
Здесь используется хитрость: так как оба прохода используют «окно» шириной в 1 пиксель, я добавляю однопиксельный бордюр вкоруг исходного изображения, чтобы избежать проверки границ. Для негатива бордюр тоже нужно изменить на противоположное значение, чего не было учтено в [3].
Полноценный рабочий алгоритм можно посмотреть в генераторе растровых шрифтов с открытым исходным кодом UBFG. Пример результата:

Шейдерим
Идея обратного преобразования (из SDF в растровый контур) основана на увеличении контрастности до такой степени, что «размытые» края не будут видны. Изменяя контрастность SDF можно получить различные эффекты, а также регулировать качество антиалиасинга изображения. В качестве примера возьмём исходник:
Это тоже SDF, просто сильно сжатый и уменьшенный в размере. Увеличим его в 16 раз:
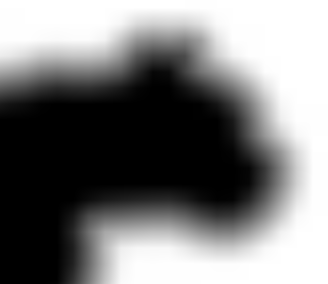
Теперь, чтобы получить красивый контур, увеличим контрастность. Я для этих целей использовал GIMP:

Чтобы увидеть результат использования SDF в реальном времени, без шейдеров не обойтись. Простейший альфа-тест также может применяться, но он рубит на корню антиалиасинг. Однако используемый шейдер представляет собой всего пару инструкций и фактически не влияет на производительность. Более того, учитывая что шейдеры сейчас дешёвые, а память/кэш дорогие — можно получить неплохое ускорение за счёт экономии видеопамяти.
Теперь посмотрим, как это дело можно использовать в OpenGL. Все примеры будут даны в виде чистого GLSL исходного кода. Опробовать можно в любом шейдерном редакторе. Все примеры я тестировал в редакторе Kick.js, поскольку это единственный редактор, который позволяет загрузить свои текстуры.
Простейший быстрый вариант
precision highp float;
uniform sampler2D tex;
const float contrast = 40.;
void main(void)
{
vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.3).xxx;
gl_FragColor = vec4((c-0.5)*contrast,1.0);
}
Здесь просто вытягиваем контраст относительно среднего значения (0.5). Сила контраста должна варьироваться в зависимости от масштаба текстуры и размазанности карты DF — параметр подбирается экспериментально и задаётся через uniform с множителем масштаба.
Немного улучшить качество можно фильтром
smoothstep:precision highp float;
uniform sampler2D tex;
const float threshold = .01;
void main(void)
{
vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.3).xxx;
vec3 res = smoothstep(.5-threshold, .5+threshold, c);
gl_FragColor = vec4(res,1.0);
}
Здесь порог также нужно подобрать.
smoothstep чуть медленнее на старых видеокартах и телефонах.Эффект outline
Чтобы получить такой эффект, нужно взять два порога и инвертировать цвет:
precision highp float;
uniform sampler2D tex;
const float contrast = 20.;
void main(void)
{
vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx;
vec3 c1 = (c-.45) * contrast;
vec3 c2 = 1.-(c-.5) * contrast;
vec3 res = mix(c1, c2, (c-.5)*contrast);
gl_FragColor = vec4(res,1.0);
}
Результат:

Эффект свечения и тени
Чуть похимичить над предыдущим примером — и получаем эффект свечения:
precision highp float;
uniform sampler2D tex;
const float contrast = 20.;
const float glow = 2.;
void main(void)
{
vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx;
vec3 c1 = clamp((c-.5)*contrast,0.,1.);
vec3 c2 = clamp(1.-(c-.5)/glow, 0., 1.);
vec3 res = 1.-mix(c1, c2, (c-.5)*contrast);
gl_FragColor = vec4(res,1.0);
}
Чтобы получилась тень, нужно взять цвет для glow со смещением:
precision highp float;
uniform sampler2D tex;
const float contrast = 20.;
const float glow = 2.;
void main(void)
{
vec3 c = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35).xxx;
vec3 gc = texture2D(tex,gl_FragCoord.xy/vec2(256., 128.)*.35 + vec2(-0.02,0.02)).xxx;
vec3 c1 = clamp((c-.5)*contrast,0.,1.);
vec3 c2 = clamp(1.-(gc-.5)/glow, 0., 1.);
vec3 res = 1.-mix(c1, c2, (c-.5)*contrast);
gl_FragColor = vec4(res,1.0);
}
Результат:

Результат может показаться не ахти, но это потому что я использовал слишком маленькую карту:
Ссылки
[1] Improved Alpha-Tested Magnification for Vector Textures and Special Effects — та самая статья от Valve.
[2] Frank Y. Shih, Yi-Ta Wu. Fast Euclidean distance transformation in two scans using a 3x3 neighborhood — китайцы? Нет, всего лишь университет Нью Джерси.
[3] www.codersnotes.com/notes/signed-distance-fields — тут тоже довольно быстрый алгоритм, но к сожалению его автор допустил несколько ошибок и присутствует умножение, что чуть медленнее алгоритма, представленного в этой статье.
[4] contourtextures.wikidot.com — ещё одна реализация расчёта SDF, но её преимущество в том, что может учитывать сглаживание краёв для определения ближайших точек. Насчёт производительности ничего не говорится, но хорош, когда нет возможности получить оригинал высокого разрешения (с другой стороны можно просто обойтись трюком с upscale). Если был опыт использования — отписывайтесь в комментариях.
[5] gpuhacks.wordpress.com/2013/07/08/signed-distance-field-rendering-of-color-bit-planes — метод рендеринга цветных векторных изображений (подходит для небольшого количества цветов).
[6] distance.sourceforge.net — интересный ресурс, на котором сравниваются различные алгоритмы подсчёта SDF.
upd. Спасибо замечанию Bas1l, алгоритм всё-таки не совсем точный и может давать ошибки на вычислении расстояния до ближайших соседей из-за ошибки в доказательстве. В этой статье представлена улучшенная версия алгоритма.
upd2. От пользователя achkasov замечание по части шейдеров. В случае резких переходов на SDF карте могут появляться заплывы и неравномерный антиалиасинг. Подробнее об эффекте и о том, как с этим бороться: iquilezles.org/www/articles/distance/distance.htm
Изменив шейдр, получаем значительное улучшение в области, кхм, хвоста:

Код GLSL
precision highp float;
uniform sampler2D tex;
const float contrast = 2.;
float f(vec2 p)
{
return texture2D(tex,p).x - 0.5;
}
vec2 grad(vec2 p)
{
vec2 h = vec2( 4./256.0, 0.0 );
return vec2( f(p+h.xy) - f(p-h.xy),
f(p+h.yx) - f(p-h.yx) )/(2.0*h.x);
}
void main(void)
{
vec2 p = gl_FragCoord.xy/vec2(256., 128.)*.35;
//float c = texture2D(tex,p).x;
float v = f(p);
vec2 g = grad(p);
float c = (v)/length(g);
float res = c * 300.;
gl_FragColor = vec4(res,res,res, 1.0);
}