На хабре уже был рассмотрен муравьиный алгоритм, позволяющий используя простые правила решить задачу поиска оптимального маршрута. В данной статье рассмотрено применение этого алгоритма к задаче классификации.
Впервые применение алгоритма муравьиной колонии для классификации было представлено R. Parpinelli в 2002 году. Метод извлечения классификационных правил на основе муравьиного алгоритма получил название AntMiner.
Цель метода — получить простые правила вида если условие то следствие.
Предполагается, что все атрибуты категориальны. Т.е. термы представлены в виде Атрибут = Значение, например Пол = Мужской. AntMiner последовательно формирует упорядоченный список правил. Вычисление начинается с пустого множества правил и после формирования первого, все тестовые единицы данных, покрытые этим правилом, удаляются из тестового набора.
Алгоритм использует при работе направленный граф, где каждому атрибуту сопоставляется столько вершин, сколько возможных значений он принимает в тестовом наборе. Соответственно, предполагается, что перед началом работы алгоритма из тестового набора выделены множества атрибутов и их возможных значений, а также множество возможных классов.
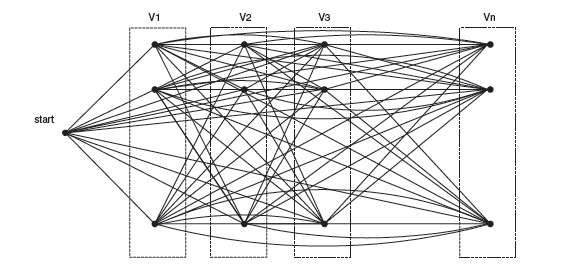
Псевдокод алгоритма выглядит следующим образом:
Рассмотрим последовательно шаги алгоритма.
Все ребра графа инициализируются начальным значением феромона по следующей формуле:
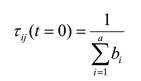
, где a — общее число атрибутов, bi — количество возможных значений i-го атрибута.
Каждое правило в алгоритме AntMiner содержит антецедент (набор термов Атрибут = Значение) и представляемый им класс. В оригинальном алгоритме исходные данные содержат только категориальные атрибуты. Предположим, что термij ≈ Ai = Vij, где Ai это i-й атрибут, а Vij это j-ое значение Ai.
Вероятность, что этот терм будет добавлен в текущее частичное правило, составляемое муравьём определяется следующей формулой:
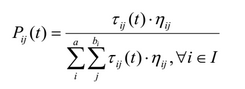
, где ηij это значение эвристики (будет определена далее), τij значение феромона на этом ребре графа, а I множество атрибутов, еще не использованных текущим муравьём.
В традиционном алгоритме муравьиной колонии для решения транспортной задачи веса ребер используются совместно со значением феромона для принятия решения о выборе следующей вершины. В алгоритме AntMiner эвристикой является количество информации — термин, использующийся в теории информации. Качеством здесь измеряется с помощью энтропии, для предпочтения одних правил над другими:
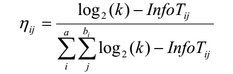
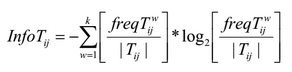
где k — число классов, Tij — подмножество, содержащее все единицы данных, где атрибут Ai имеет значение Vij, |Tij| число элементов в Tij, freq(Twij) — число единиц данных, имеющих класс w, а — общее число атрибутов, bi — число возможных значений i-го атрибута.
Чем выше значение Info Tij, тем меньше шансов что муравей выберет данный терм.
После того как каждый муравей завершит конструирование правила, выполняется обновление феромонов по следующей формуле:
τij(t +1) =τ ij(t)+τij(t).Q ∀термij∈текущее правило
где Q — качество правила, которое вычисляется по следующей формуле:
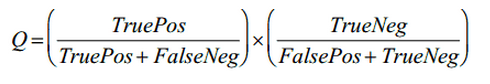
Здесь TruePos — количество единиц данных, которые покрываются правилом и класс которых совпадает с классом, представляемым правилом, FaslePos — количество единиц данных, которые покрываются правилом, но класс которых отличается от класса, представляемым правилом, TrueNeg — количество единиц данных, которые не покрываются правилом и класс которых не совпадает с классом, представляемым правилом, FalseNeg — количество единиц данных, которые не покрываются правилом, но класс которых совпадает с классом, представляемым правилом.
Также требуется выполнять пересчёт феромонов, имитирующий его испарение. Это можно сделать простой нормализацией значений с учётом обновленного значения феромонов.
Для более гибкой настройки выполнения алгоритма используется следующая формула обновления вероятностей ребер принадлежащих текущему правилу:
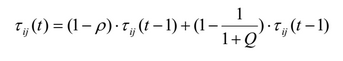
где р – коэффициент испарения (обычно устанавливается значение ~0,1), Q качество правила, описанное выше. Ребра, не покрытые текущим правилом просто нормализуются. Этот способ обеспечивает снижение значения феромона при низком Q и повышение при высоком (в отличие от оригинального способа).
Также можно улучшить сходимость алгоритма, вводя некоторое число так называемых “элитных” муравьёв, которые выбирают терм, для которого P = max Pij.
В оригинальном алгоритме выбор терм выбирается по следующему алгоритму:
Где q случайная величина [0..1] с равномерным распределением. Т.е. используется плотность вероятностей термов.
Для введения элитных муравьёв алгоритм выбора терма изменяется следующим образом:
Здесь q1 и q2 случайные величины [0..1] с равномерным распределением.
Аналогом AntMiner является известный алгоритм Naive Bayes. Согласно моим экспериментам по их сравнению AntMiner либо незначительно превосходит Naive Bayes, либо и вовсе уступает ему на различных наборах данных. Для сравнения использовалась реализация AntMiner представленная здесь и реализация Naive Bayes из библиотеки WEKA. Кроме того, AntMiner значительно уступает и по времени вычисления. Возможно, есть ситуации или некоторые предусловия, при которых AntMiner оказывается действительно лучшим выбором.
Впервые применение алгоритма муравьиной колонии для классификации было представлено R. Parpinelli в 2002 году. Метод извлечения классификационных правил на основе муравьиного алгоритма получил название AntMiner.
Цель метода — получить простые правила вида если условие то следствие.
Предполагается, что все атрибуты категориальны. Т.е. термы представлены в виде Атрибут = Значение, например Пол = Мужской. AntMiner последовательно формирует упорядоченный список правил. Вычисление начинается с пустого множества правил и после формирования первого, все тестовые единицы данных, покрытые этим правилом, удаляются из тестового набора.
Алгоритм использует при работе направленный граф, где каждому атрибуту сопоставляется столько вершин, сколько возможных значений он принимает в тестовом наборе. Соответственно, предполагается, что перед началом работы алгоритма из тестового набора выделены множества атрибутов и их возможных значений, а также множество возможных классов.

Псевдокод алгоритма выглядит следующим образом:
testSet = Весь тестовый набор ПОКА (|testSet| > макс_число_непокрытых_случаев) i = 0; ВЫПОЛНЯТЬ i = i + 1; i-й муравей последовательно строит классификационное правило; Обновление феромонов на пути, представленным правилом i-го муравья; ПОКА (i < Число_муравьёв) Выбрать лучшее из всех правил; testSet = случаи, не покрытые лучшим правилом; КОНЕЦ ЦИКЛА
Рассмотрим последовательно шаги алгоритма.
Инициализация значений феромона
Все ребра графа инициализируются начальным значением феромона по следующей формуле:
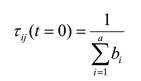
, где a — общее число атрибутов, bi — количество возможных значений i-го атрибута.
Построение правила
Каждое правило в алгоритме AntMiner содержит антецедент (набор термов Атрибут = Значение) и представляемый им класс. В оригинальном алгоритме исходные данные содержат только категориальные атрибуты. Предположим, что термij ≈ Ai = Vij, где Ai это i-й атрибут, а Vij это j-ое значение Ai.
Вероятность, что этот терм будет добавлен в текущее частичное правило, составляемое муравьём определяется следующей формулой:
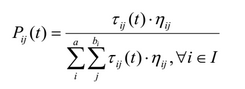
, где ηij это значение эвристики (будет определена далее), τij значение феромона на этом ребре графа, а I множество атрибутов, еще не использованных текущим муравьём.
Эвристика
В традиционном алгоритме муравьиной колонии для решения транспортной задачи веса ребер используются совместно со значением феромона для принятия решения о выборе следующей вершины. В алгоритме AntMiner эвристикой является количество информации — термин, использующийся в теории информации. Качеством здесь измеряется с помощью энтропии, для предпочтения одних правил над другими:
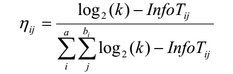
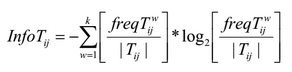
где k — число классов, Tij — подмножество, содержащее все единицы данных, где атрибут Ai имеет значение Vij, |Tij| число элементов в Tij, freq(Twij) — число единиц данных, имеющих класс w, а — общее число атрибутов, bi — число возможных значений i-го атрибута.
Чем выше значение Info Tij, тем меньше шансов что муравей выберет данный терм.
Обновление значений феромонов
После того как каждый муравей завершит конструирование правила, выполняется обновление феромонов по следующей формуле:
τij(t +1) =τ ij(t)+τij(t).Q ∀термij∈текущее правило
где Q — качество правила, которое вычисляется по следующей формуле:
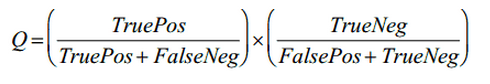
Здесь TruePos — количество единиц данных, которые покрываются правилом и класс которых совпадает с классом, представляемым правилом, FaslePos — количество единиц данных, которые покрываются правилом, но класс которых отличается от класса, представляемым правилом, TrueNeg — количество единиц данных, которые не покрываются правилом и класс которых не совпадает с классом, представляемым правилом, FalseNeg — количество единиц данных, которые не покрываются правилом, но класс которых совпадает с классом, представляемым правилом.
Также требуется выполнять пересчёт феромонов, имитирующий его испарение. Это можно сделать простой нормализацией значений с учётом обновленного значения феромонов.
Улучшенное обновление феромонов
Для более гибкой настройки выполнения алгоритма используется следующая формула обновления вероятностей ребер принадлежащих текущему правилу:
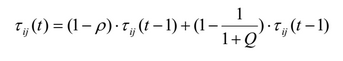
где р – коэффициент испарения (обычно устанавливается значение ~0,1), Q качество правила, описанное выше. Ребра, не покрытые текущим правилом просто нормализуются. Этот способ обеспечивает снижение значения феромона при низком Q и повышение при высоком (в отличие от оригинального способа).
Элитные муравьи
Также можно улучшить сходимость алгоритма, вводя некоторое число так называемых “элитных” муравьёв, которые выбирают терм, для которого P = max Pij.
В оригинальном алгоритме выбор терм выбирается по следующему алгоритму:
ДЛЯ ВСЕХ (i,j)∈ Ji ЕСЛИ q ≤ ∑ Pij ТО Выбрать термij
Где q случайная величина [0..1] с равномерным распределением. Т.е. используется плотность вероятностей термов.
Для введения элитных муравьёв алгоритм выбора терма изменяется следующим образом:
ЕСЛИ q1 ≤ ϕ ТО ДЛЯ ВСЕХ (i,j)∈ Ji ЕСЛИ q2 ≤ ∑ Pij ТО Выбрать термij ИНАЧЕ Выбрать терм с P = max Pij
Здесь q1 и q2 случайные величины [0..1] с равномерным распределением.
Некоторые наблюдения
Аналогом AntMiner является известный алгоритм Naive Bayes. Согласно моим экспериментам по их сравнению AntMiner либо незначительно превосходит Naive Bayes, либо и вовсе уступает ему на различных наборах данных. Для сравнения использовалась реализация AntMiner представленная здесь и реализация Naive Bayes из библиотеки WEKA. Кроме того, AntMiner значительно уступает и по времени вычисления. Возможно, есть ситуации или некоторые предусловия, при которых AntMiner оказывается действительно лучшим выбором.