Создавая дополнения к отечественной математической программе SMath Studio, я нашёл в сети ряд библиотек, которые можно было бы использовать в своих программах. Предлагаю небольшой их обзор.
Стандартный RK45 с фиксированным шагом может помочь в большинстве случаев, но бывают задачи, где этого недостаточно. Для решения жёстких систем были придуманы специальные решатели, которые мы и рассмотрим с точки зрения их практического использования.
Большинство представленных ниже функций, если не оговорено особо, можно привести к одному формату вызова (по аналогии с Mathcad):
ode_solver( init, x1, x2, intvls, D(t, x) )
где:
- init — вектор начальных условий,
- (x1, x2) — отрезок интегрирования,
- intvls — количество интервалов на отрезке,
- D(t, x) — система ОДУ.
1. Intel ODE Solvers Library
Содержит следующие функции: rkm9st(), mk52lfn(), mk52lfa(), rkm9mkn(), rkm9mka().
- rkm9st() — a specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.
- mk52lfn() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.
- mk52lfa() — a specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.
- rkm9mkn() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.
- rkm9mka() — a specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.
Библиотека написана на C со всеми вытекающими отсюда зависимостями. Доступны 32- и 64-разрядные версии библиотеки (libiode_ia32.lib и libiode_intel64.lib).
intel_ode.h
/*******************************************************************************
! INTEL CONFIDENTIAL
! Copyright(C) 2007-2008 Intel Corporation. All Rights Reserved.
! The source code contained or described herein and all documents related to
! the source code ("Material") are owned by Intel Corporation or its suppliers
! or licensors. Title to the Material remains with Intel Corporation or its
! suppliers and licensors. The Material contains trade secrets and proprietary
! and confidential information of Intel or its suppliers and licensors. The
! Material is protected by worldwide copyright and trade secret laws and
! treaty provisions. No part of the Material may be used, copied, reproduced,
! modified, published, uploaded, posted, transmitted, distributed or disclosed
! in any way without Intel's prior express written permission.
! No license under any patent, copyright, trade secret or other intellectual
! property right is granted to or conferred upon you by disclosure or delivery
! of the Materials, either expressly, by implication, inducement, estoppel or
! otherwise. Any license under such intellectual property rights must be
! express and approved by Intel in writing.
!
!******************************************************************************
!
! Header file for Intel(R) ODE Solvers
!
!*******************************************************************************/
#ifndef _INTEL_ODE_H_
#define _INTEL_ODE_H_
#ifdef __cplusplus
extern "C" {
#endif /* __cplusplus */
void dodesol(int*,int*,double*,double*,double*,void*,void*,\
double*,double*,double*,double*,double*,int*,int*);
void dodesol_rkm9st(int*,int*,double*,double*,double*,void*,\
double*,double*,double*,double*,double*,int*);
void dodesol_mk52lfn(int*,int*,double*,double*,double*,void*,\
double*,double*,double*,double*,double*,int*,int*);
void dodesol_mk52lfa(int*,int*,double*,double*,double*,void*,void*,\
double*,double*,double*,double*,double*,int*,int*);
void dodesol_rkm9mkn(int*,int*,double*,double*,double*,void*,\
double*,double*,double*,double*,double*,int*,int*);
void dodesol_rkm9mka(int*,int*,double*,double*,double*,void*,void*,\
double*,double*,double*,double*,double*,int*,int*);
#ifdef __cplusplus
}
#endif /* __cplusplus */
#endif /* _INTEL_ODE_H_ */Дополнение ODE Solvers демонстрирует работу с этой библиотекой из c# кода.
Ссылки:
1. Intel Ordinary Differential Equations Solver Library.
2. Исходники дополнения ODESolvers.
2. GNU Scientific Library (GSL)
Содержит следующие функции: rk2(), rk4(), rkf45(), rkck(), rk8pd(), rk1imp(), rk2imp(), rk4imp(), bsimp(), msadams(), msbdf().
Часть из них требует дополнительные параметры для работы (Якобиан). Те, которые мне удалось привести к общему виду:
Solvers for Non-Stiff Systems:
- rk2() — explicit embedded Runge-Kutta (2, 3) method.
- rk4() — explicit 4th order (classical) Runge-Kutta. Error estimation is carried out by the step doubling method.
- rkf45() — explicit embedded Runge-Kutta-Fehlberg (4, 5) method.
- rkck() — explicit embedded Runge-Kutta Cash-Karp (4, 5) method.
- rk8pd() — explicit embedded Runge-Kutta Prince-Dormand (8, 9) method.
Остальные:
- rk1imp() — Implicit Gaussian first order Runge-Kutta. Also known as implicit Euler or backward Euler method. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- rk2imp() — Implicit Gaussian second order Runge-Kutta. Also known as implicit mid-point rule. Error estimation is carried out by the step doubling method. This stepper requires the Jacobian.
- rk4imp() — Implicit Gaussian 4th order Runge-Kutta. Error estimation is carried out by the step doubling method. This algorithm requires the Jacobian.
- bsimp() — Implicit Bulirsch-Stoer method of Bader and Deuflhard. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
- msadams() — A variable-coefficient linear multistep Adams method in Nordsieck form. This stepper uses explicit Adams-Bashforth (predictor) and implicit Adams-Moulton (corrector) methods in P(EC)^m functional iteration mode. Method order varies dynamically between 1 and 12.
- msbdf() — A variable-coefficient linear multistep backward differentiation formula (BDF) method in Nordsieck form. This stepper uses the explicit BDF formula as predictor and implicit BDF formula as corrector. A modified Newton iteration method is used to solve the system of non-linear equations. Method order varies dynamically between 1 and 5. The method is generally suitable for stiff problems. This stepper requires the Jacobian.
Для работы с функциями используется универсальный интерфейс, где конкретный тип решателя задаёт шаговую функцию. Дополнение GNUScientificLibrary демонстрирует работу с этой библиотекой из c# кода.
Не так просто сделать сборку библиотеки под Windows. Я использовал инструкцию с одного сайта, который сейчас недоступен. Тем не менее, в репозитории дополнения вы сможете найти 32- и 64-разрядные версии
Ссылки:
1. GSL. Ordinary Differential Equations.
2. Исходники дополнения GNUScientificLibrary.
3. Matlab C++ Math Library 2.1 (Win32)
Да, вы можете использовать эту старую версию run-time библиотек для расчётов. Более того, она может быть установлена по относительным путям, т.е. можно просто положить содержимое оригинального дистрибутива (~28 Мб в развёрнутом виде) рядом со своей программой. Правда при вызове функций придётся использовать SetCurrentDirectory() с прямым указанием на место расположения «bin\win32». Я так делаю в своём дополнении.
Содержит следующие функции: ode23(), ode45(), ode113(), ode15s(), ode23s().
- ode23() — solve nonstiff differential equations; low order method,
- ode45() — solve nonstiff differential equations; medium order method,
- ode113() — solve nonstiff differential equations; variable order method,
- ode15s() — solve stiff differential equations and DAEs; variable order method,
- ode23s() — solve stiff differential equations; low order method.
Дополнение MatlabCppMathLibrary демонстрирует работу с этой библиотекой из c# кода.
Ссылки:
1. Ordinary Differential Equations.
2. MATLAB C++ Math Library. User's Guide. Version 2.1 (pdf).
3. MATLAB C++ Math Library. Reference. Version 2 (pdf).
4. Исходники дополнения MatlabCppMathLibrary.
4. Octave C++ Math Library (Win32)
Примерно то же самое, что и Matlab C++ Math Library, но со своими тараканами. К сожалению, работу с этой библиотекой я одолел только частично. Дополнение OctaveCppMathLibrary демонстрирует работу с этой библиотекой из c# кода.
Ссылки:
1. Ordinary Differential Equations.
2. Исходники дополнения OctaveCppMathLibrary.
5. DotNumerics
Содержит следующие функции: AdamsMoulton(), ExplicitRK45(), ImplicitRK5(), GearsBDF(). Эта библиотека портирована для .Net с фортрана. Она понравилась мне больше всего. Работает достаточно быстро.
Solvers for Non-Stiff Systems:
- AdamsMoulton() — solves an initial-value problem for nonstiff ordinary differential equations using the Adams-Moulton method.
- ExplicitRK45() — solves an initial-value problem for nonstiff ordinary differential equations using the explicit Runge-Kutta method of order (4)5.
Solvers for Stiff Systems:
- ImplicitRK5() — solves an initial-value problem for stiff ordinary differential equations using the implicit Runge-Kutta method of order 5.
- GearsBDF() — solves an initial-value problem for stiff ordinary differential equations using the Gear’s BDF method.
Имеется много перегрузок для различных форматов вызова функций. Дополнение DotNumerics демонстрирует работу с этой библиотекой.
Ссылки:
1. DotNumerics.
2. Исходники дополнения DotNumerics.
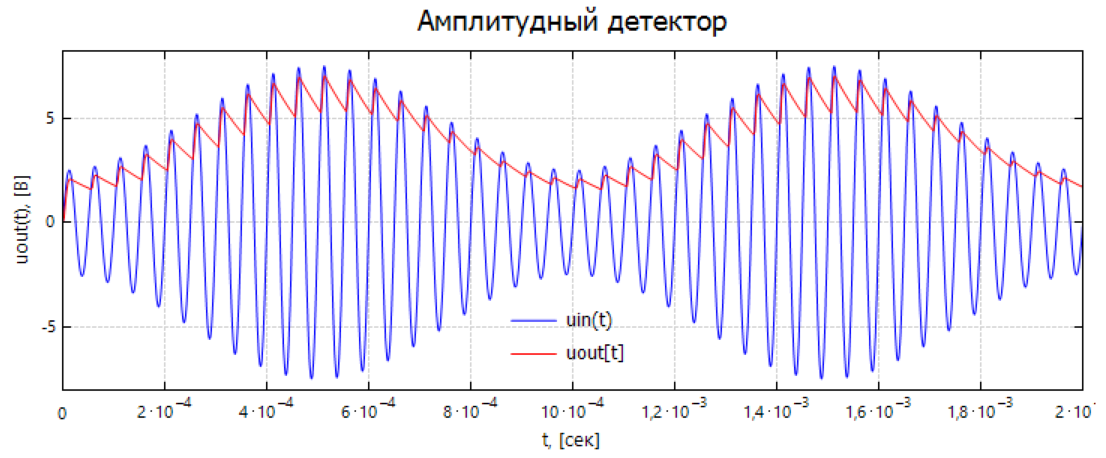
Как выглядит модель амплитудного детектора в SMath Studio при решении ОДУ с помощью функции GearsBDF():
SMath Studio


Обновление (12.07.2014).
6. boost::odeint
Содержит следующие алгоритмы:
- Explicit Euler
- Modified Midpoint
- Runge-Kutta 4
- Cash-Karp
- Dormand-Prince 5
- Fehlberg 78
- Adams Bashforth
- Adams Moulton
- Adams Bashforth Moulton
- Controlled Runge-Kutta
- Dense Output Runge-Kutta
- Bulirsch-Stoer
- Bulirsch-Stoer Dense Output
- Implicit Euler
- Rosenbrock 4
- Controlled Rosenbrock 4
- Dense Output Rosenbrock 4
- Symplectic Euler
- Symplectic RKN McLachlan
- Symplectic RKN McLachlan
Живьём не пробовал, показать пример использования не могу.
Ссылки:
1. Boost.Numeric.Odeint.
2. Stepper overview.
7. SADEL (Sets of Algebraic and Differential Equations solvers Library)
Живьём не пробовал, показать пример использования не могу.
Ссылки:
1. О библиотеке SADEL.
2. Сравнение современных решателей жестких систем обыкновенных дифференциальных уравнений с решателями Си библиотеки SADEL.
8. Решатель Лимонова А. Г.
Живьём не пробовал, показать пример использования не могу.
Ссылки:
1. Диссертация. Разработка двухстадийных схем Розенброка с комплексными коэффициентами и их применение в задачах моделирования образования периодических наноструктур, 2010.