 Иногда так бывает: задачу можно решить чуть ли не арифметически, а на ум прежде всего приходят всякие интегралы Лебега и функции Бесселя. Вот начинаешь обучать нейронную сеть, потом добавляешь еще парочку скрытых слоев, экспериментируешь с количеством нейронов, функциями активации, потом вспоминаешь о SVM и Random Forest и начинаешь все сначала. И все же, несмотря на прямо таки изобилие занимательных статистических методов обучения, линейная регрессия остается одним из популярных инструментов. И для этого есть свои предпосылки, не последнее месте среди которых занимает интуитивность в интерпретации модели.
Иногда так бывает: задачу можно решить чуть ли не арифметически, а на ум прежде всего приходят всякие интегралы Лебега и функции Бесселя. Вот начинаешь обучать нейронную сеть, потом добавляешь еще парочку скрытых слоев, экспериментируешь с количеством нейронов, функциями активации, потом вспоминаешь о SVM и Random Forest и начинаешь все сначала. И все же, несмотря на прямо таки изобилие занимательных статистических методов обучения, линейная регрессия остается одним из популярных инструментов. И для этого есть свои предпосылки, не последнее месте среди которых занимает интуитивность в интерпретации модели.Немного формул
В простейшем случае линейную модель можно представить так:
yi= a0 + a1xi + εi
где a0 — математическое ожидание зависимой переменной yi, когда переменная xi равна нулю; a1 — ожидаемое изменение зависимой переменной yi при изменении xi на единицу (этот коэффициент подбирают таким образом, чтобы величина ½Σ(yi-ŷi)2 была минимальна — это так называемая «функция невязки»); εi — случайная ошибка.
При этом коэффициенты a1 и a0 можно выразить через
â1 = cor(y, x)σy/σx
â0 = ȳ — â1x̄
Диагностика и ошибки модели
Чтобы модель была корректной, необходимо выполнение условий Гаусса-Маркова, т.е. ошибки должны быть гомоскедастичны с нулевым математическим ожиданием. График остатков ei = yi — ŷi помогает определить, насколько адекватна построенная модель (ei можно считать оценкой εi).
Посмотрим на график остатков в случае простой линейной зависимости y1 ~ x (здесь и далее все примеры приводятся на языке R):
Скрытый текст
set.seed(1)
n <- 100
x <- runif(n)
y1 <- x + rnorm(n, sd=.1)
fit1 <- lm(y1 ~ x)
par(mfrow=c(1, 2))
plot(x, y1, pch=21, col="black", bg="lightblue", cex=.9)
abline(fit1)
plot(x, resid(fit1), pch=21, col="black", bg="lightblue", cex=.9)
abline(h=0)
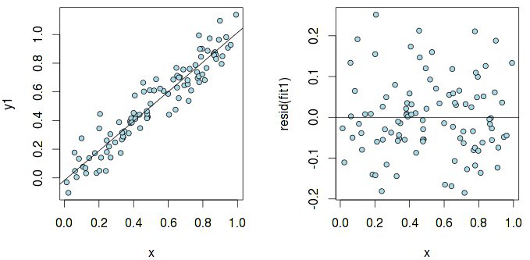
Остатки более-менее равномерно распределены относительно горизонтальной оси, что говорит об «отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях». А теперь исследуем такой же график, но построенный для линейной модели, которая на самом деле не является линейной:
Скрытый текст
y2 <- log(x) + rnorm(n, sd=.1)
fit2 <- lm(y2 ~ x)
plot(x, y2, pch=21, col="black", bg="lightblue", cex=.9)
abline(fit2)
plot(x, resid(fit2), pch=21, col="black", bg="lightblue", cex=.9)
abline(h=0)
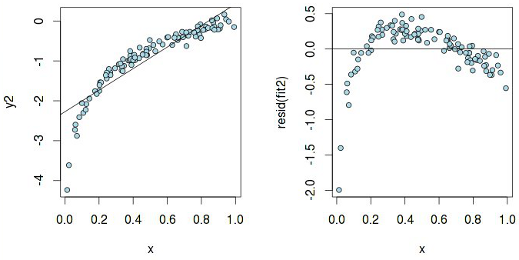
По графику y2 ~ x вроде бы можно предположить линейную зависимость, но у остатков есть паттерн, а значит, чистая линейная регрессия тут не пройдет. А вот что на самом деле означает гетероскедастичность:
Скрытый текст
y3 <- x + rnorm(n, sd=.001*x)
fit3 <- lm(y3 ~ x)
plot(x, y3, pch=21, col="black", bg="lightblue", cex=.9)
abline(fit3)
plot(x, resid(fit3), pch=21, col="black", bg="lightblue", cex=.9)
abline(h=0)
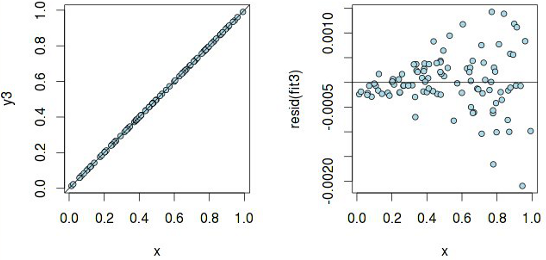
Линейная модель с такими «раздувающимися» остатками не корректна. Еще иногда бывает полезно построить график квантилей остатков против квантилей, которые можно было бы ожидать при условии, что остатки нормально распределены:
Скрытый текст
qqnorm(resid(fit1))
qqline(resid(fit1))
qqnorm(resid(fit2))
qqline(resid(fit2))
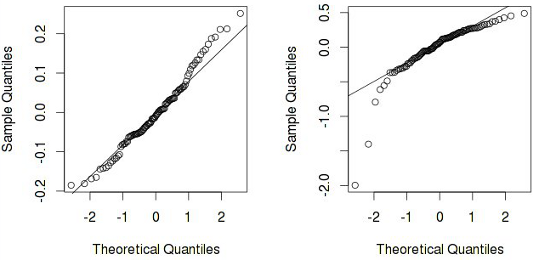
На втором графике четко видно, что предположение о нормальности остатков можно отвергнуть (что опять таки говорит о некорректности модели). А еще бывают такие ситуации:
Скрытый текст
x4 <- c(9, x)
y4 <- c(3, x + rnorm(n, sd=.1))
fit4 <- lm(y4 ~ x4)
par(mfrow=c(1, 1))
plot(x4, y4, pch=21, col="black", bg="lightblue", cex=.9)
abline(fit4)
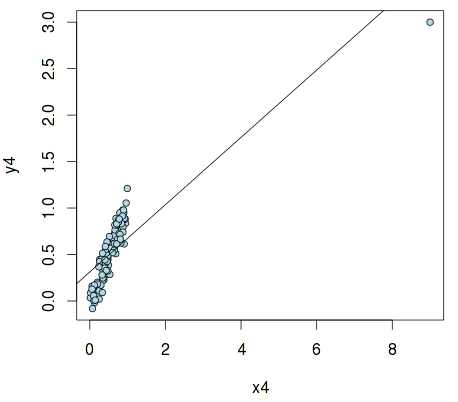
Это так называемый «выброс», который может сильно исказить результаты и привести к ошибочным выводам. В R есть средства для его обнаружения — с помощью стандартизованой меры dfbetas и hat values:
> round(dfbetas(fit4), 3)
(Intercept) x4
1 15.987 -26.342
2 -0.131 0.062
3 -0.049 0.017
4 0.083 0.000
5 0.023 0.037
6 -0.245 0.131
7 0.055 0.084
8 0.027 0.055
.....
> round(hatvalues(fit4), 3)
1 2 3 4 5 6 7 8 9 10...
0.810 0.012 0.011 0.010 0.013 0.014 0.013 0.014 0.010 0.010...
Как видно, первый член вектора x4 оказывает заметно большее влияние на параметры регрессионной модели, нежели остальные, являясь, таким образом, выбросом.
Выбор модели при множественной регрессии
Естественно, что при множественной регрессии возникает вопрос: стоит ли учитывать все переменные? С одной стороны, казалось бы, что стоит, т.к. любая переменная потенциально несет полезную информацию. Кроме того, увеличивая количество переменных, мы увеличиваем и R2 (кстати, именно по этой причине эту меру нельзя считать надежной при оценке качества модели). С другой стороны, стоить помнить о таких вещах, как AIC и BIC, которые вводят штрафы за сложность модели. Абсолютное значение информационного критерия само по себе не имеет смысла, поэтому надо сравнивать эти значения у нескольких моделей: в нашем случае — с разным количеством переменных. Модель с минимальным значением информационного критерия будет наилучшей (хотя тут есть о чем поспорить).
Рассмотрим датасет UScrime из библиотеки MASS:
library(MASS)
data(UScrime)
stepAIC(lm(y~., data=UScrime))
Модель с наименьшим значением AIC имеет следующие параметры:
Call:
lm(formula = y ~ M + Ed + Po1 + M.F + U1 + U2 + Ineq + Prob,
data = UScrime)
Coefficients:
(Intercept) M Ed Po1 M.F U1 U2 Ineq Prob
-6426.101 9.332 18.012 10.265 2.234 -6.087 18.735 6.133 -3796.032
Таким образом, оптимальная модель с учетом AIC будет такой:
fit_aic <- lm(y ~ M + Ed + Po1 + M.F + U1 + U2 + Ineq + Prob, data=UScrime)
summary(fit_aic)
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -6426.101 1194.611 -5.379 4.04e-06 ***
M 9.332 3.350 2.786 0.00828 **
Ed 18.012 5.275 3.414 0.00153 **
Po1 10.265 1.552 6.613 8.26e-08 ***
M.F 2.234 1.360 1.642 0.10874
U1 -6.087 3.339 -1.823 0.07622 .
U2 18.735 7.248 2.585 0.01371 *
Ineq 6.133 1.396 4.394 8.63e-05 ***
Prob -3796.032 1490.646 -2.547 0.01505 *
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Если внимательно присмотреться, то окажется, что у переменных M.F и U1 довольно высокое значение p-value, что как бы намекает нам, что эти переменные не так уж и важны. Но p-value — довольно неоднозначная мера при оценки важности той или иной переменной для статистической модели. Наглядно этот факт демонстрирует пример:
data <- read.table("http://www4.stat.ncsu.edu/~stefanski/NSF_Supported/Hidden_Images/orly_owl_files/orly_owl_Lin_9p_5_flat.txt")
fit <- lm(V1~. -1, data=data)
summary(fit)$coef
Estimate Std. Error t value Pr(>|t|)
V2 1.1912939 0.1401286 8.501431 3.325404e-17
V3 0.9354776 0.1271192 7.359057 2.568432e-13
V4 0.9311644 0.1240912 7.503873 8.816818e-14
V5 1.1644978 0.1385375 8.405652 7.370156e-17
V6 1.0613459 0.1317248 8.057300 1.242584e-15
V7 1.0092041 0.1287784 7.836752 7.021785e-15
V8 0.9307010 0.1219609 7.631143 3.391212e-14
V9 0.8624487 0.1198499 7.196073 8.362082e-13
V10 0.9763194 0.0879140 11.105393 6.027585e-28
p-values у каждой переменной — практически нуль, и можно предположить, что все переменные важны для этой линейной модели. Но на самом деле, если присмотреться к остаткам, выходит как-то так:
Скрытый текст
plot(predict(fit), resid(fit), pch=".")

И все же, альтернативный подход основывается на дисперсионном анализе, в котором значения p-value играют ключевую роль. Сравним модель без переменной M.F с моделью, построенной с учетом только AIС:
fit_aic0 <- update(fit_aic, ~ . - M.F)
anova(fit_aic0, fit_aic)
Analysis of Variance Table
Model 1: y ~ M + Ed + Po1 + U1 + U2 + Ineq + Prob
Model 2: y ~ M + Ed + Po1 + M.F + U1 + U2 + Ineq + Prob
Res.Df RSS Df Sum of Sq F Pr(>F)
1 39 1556227
2 38 1453068 1 103159 2.6978 0.1087
Учитывая P-значение, равное 0.1087, при уровне значимости α=0.05 мы можем сделать вывод, что нет статистически значимого свидетельства в пользу альтернативной гипотезы, т.е. в пользу модели с дополнительной переменной M.F.
Ссылки:
Only registered users can participate in poll. Log in, please.
Нужен ли на Хабре MathJax?
87.56% Да197
12.44% Нет28
225 users voted. 63 users abstained.