Недавно на Хабре появилась удивительная статья «Папа, а почему на ноль делить нельзя?», которая собрала массу не менее удивительных комментариев.
Детские вопросы обычно очень сложны («Почему небо ночью темное?», «Почему яблоки падают на землю?») и у взрослых обычно не хватает времени, чтобы их доходчиво объяснить. Да и не всегда взрослые знают ответ на эти вопросы.
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем. Наверное, виной тому какие-то изъяны в методике преподавания математики в средней школе, в трудностях перехода от изучения арифметики к изучению буквенной алгебры и свойств элементарных функций.
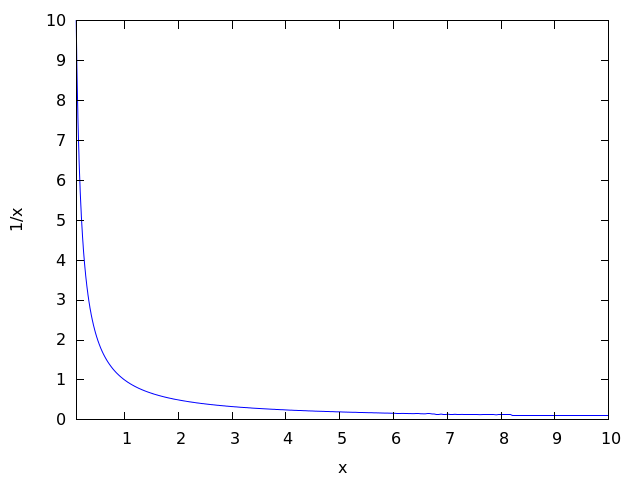
Самые серьезные сомнения появляются, я думаю, после изучения рациональных чисел, когда для любого числа x, кроме нуля, вводится понятие обратного числа 1/x, и графика гиперболы y(x)=1/x.
Очевидно, что при делении 1 на очень маленькие числа появляются очень большие числа, и чем меньше мы берем x, тем больше становится 1/x. Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?
Алгебраическое возражение против этого состоит в следующем. Предположим, что ∞=1/x является числом. Тогда на это число должны распространяться все правила, которые имеют место быть для обычных чисел. В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0, а из этого уже следует, что все числа равны между собой и равны нулю. В самом деле, поскольку для любого числа x верно 1⋅x=x, то 1⋅x=0⋅x=0.
«Ну разве это не полная чушь?» — спросим себя, добравшись до этого места.
Разумеется, это полная чушь, если мы говорим об обычных числах. Но я недаром подчеркнул выше слово «правила». К ним мы вернемся чуть позже, после рассмотрения арифметического возражения против деления на ноль, и поможет нам в этом фасоль.
Вернемся в те времена, когда не было ни компьютеров, ни калькуляторов, ни логарифмических линеек, и поставим перед собой задачу разделить некоторое случайное число, например, на 5.
Для этого берем чашу с фасолью, символизирующую натуральный ряд, и высыпаем из нее какое-то количество зерен на разлинованный лист бумаги:

Тем самым, мы установили делимое на нашем бобовом калькуляторе.
Задача состоит в том, чтобы разложить эти зерна на пять рядов. Чтобы не запутаться отмечаем эти ряды, то есть, устанавливаем делитель:

Теперь раскладываем зерна из кучи на пять рядов в столбик. Это значительно дольше, чем на обычном калькуляторе, зато позволяет почувствовать всю прелесть арифметики до изобретения позиционной системы счисления.

Алгоритм завершается, когда мы получаем некоторое прямоугольное число и (возможно) остаток:

В данном примере осталось 2 зерна, а рядов по 5 зерен образовалось 18. Получается, что случайное число было 18⋅5+2=92.
Ясно, что мы можем выполнить этот алгоритм для любого натурального делимого и любого натурального делителя, отличного от нуля; если же делитель равен 0, то этот алгоритм выполнить попросту невозможно.
«Подождите!» — скажет внимательный читатель. — «В рассмотренном примере мы получили остаток 2, что с ним делать?»
Это, на самом деле, очень важное замечание. Вообще говоря, мы не можем делить фасолины, не испортив наш бобовый калькулятор — мало того, что разделить 2 фасолины на 5 одинаковых частей проблематично, даже если мы их раздробим подобающим образом, мы уже не сможем их собрать.
Поэтому достаточно долго люди старались обходиться без дробей. Например, в анонимной арабской рукописи XII века описана следующая задача: «разделить 100 фунтов между 11 человеками». Поскольку 100=11⋅9+1, средневековый математик предлагает сначала раздать каждому по 9 фунтов, а затем обменять оставшийся фунт на яйца, которых, как оказывается по курсу обмена, получается ровно 91. Но 91=11⋅8+3, поэтому арабский ученый предлагает раздать каждому по 8 яиц, а три оставшихся яйца отдать тому, кто производит раздел, или же обменять на соль к яйцам.
Говоря современным математическим языком, деление проводилось в полукольце натуральных чисел. Впрочем, с таким же успехом, используя красную и белую фасоль, мы могли бы определить деление с остатком и в кольце целых чисел — в изложенном алгоритме появились бы дополнительные правила для выбора цветов используемых для вычислений зерен фасоли, но точно так же остались бы бессмысленными операции вида x/0 и 5/2.
Очевидно, что для того, чтобы придать символу 5/2 конкретный смысл, нужно изменить правила игры, и перейти к полю рациональных дробей, пополнив множество целых чисел всевозможными выражениями m/n, где m — целое, а n — натуральное.
Важно заметить, что сделать это можно не единственным способом, однако в классической арифметике рассматривается такое пополнение, в котором символ 1/n означает долю от деления 1 на n, т. е. такое число, для которого верно выражение n⋅1/n=1; при чем доли имеют смысл не при подсчете штучных предметов (например, зерен фасоли), а при измерении величин, которые предполагаются непрерывными (или хотя бы неограниченно делимыми) — длин отрезков, площадей фигур и т. д.
В поле рациональных дробей уже нет смысла рассматривать неполное частное и остатки, так как частное от любого ненулевого делителя является какой-то рациональной дробью. Более того, как и в случае с натуральными числами, мы можем использовать для деления фасоль без изменения алгоритма.
В самом деле, пусть требуется разделить рациональное число α=p/q на β=r/s. Это равносильно выполнению следующих действий:
α:β=p/q:r/s=p⋅s/q⋅r
и задача при любых рациональных α и β свелась к уже известной процедуре деления целых чисел. Это еще раз показывает, что деление на ноль не имеет никакого арифметического смысла.
«Получается, делить на ноль нельзя, даже если очень хочется?» — увы, ответ на этот вопрос положительный: мы не можем определить операцию деления на ноль исходя их естественных потребностей счета и измерений. Правда, есть две лазейки.
Первая: вместо «обычных» чисел (т.е. кольца натуральных и поля рациональных, а также поля действительных чисел, о котором я, кстати, до сих пор не сказал ни слова и расскажу как-нибудь в другой раз) рассмотреть вырожденный случай — тривиальное кольцо {0}, и положить по определению 0/0=0. В этом случае, когда нам говорят: «Все числа равны между собой и равны нулю!» — мы можем сказать невозмутимым тоном: «Ну и что? Это всегда было так».
Вторая: отказаться от некоторых привычных правил умножения. В частности, от аксиомы 0⋅x=0. Говорят, что это возможно (см. http://en.wikipedia.org/wiki/Wheel_theory). Разумеется, этот вариант гораздо интереснее первого, но и он представляет собой такое изменение правил игры, которое сразу выводит нас за рамки классической арифметики.
В заключение этой заметки хочу привести список литературы для тех, кто заинтересовался числовыми системами:
— И.В. Арнольд «Теоретическая арифметика», М, ОГИЗ 1938 — очень подробная и детальная книга, в которой можно найти описания классических числовых систем, включая кватернионы.
— Е. Г. Гонин «Теоретическая арифметика», М, 1959 — эта книга покороче и посовременнее, и тоже очень хороша, хотя не так подробна, как книга И.В. Арнольда.
— С. Феферман «Числовые системы» — классическая монография, местами достаточно сложная; в ней изложены некоторые частные вопросы, которых нет в двух других книгах по теоретической арифметике.
— А. А. Кириллов «Что такое число?» (1993) — небольшая брошюра, рассчитанная на подготовленного читателя.
— Е. Б. Дынкин, В. А. Успенский «Математические беседы» — популярная книга, рассчитанная на школьников. Содержит массу информации и задач по такой «нестандартной» теме, как p-адические числа.
Детские вопросы обычно очень сложны («Почему небо ночью темное?», «Почему яблоки падают на землю?») и у взрослых обычно не хватает времени, чтобы их доходчиво объяснить. Да и не всегда взрослые знают ответ на эти вопросы.
Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем. Наверное, виной тому какие-то изъяны в методике преподавания математики в средней школе, в трудностях перехода от изучения арифметики к изучению буквенной алгебры и свойств элементарных функций.

Самые серьезные сомнения появляются, я думаю, после изучения рациональных чисел, когда для любого числа x, кроме нуля, вводится понятие обратного числа 1/x, и графика гиперболы y(x)=1/x.
Очевидно, что при делении 1 на очень маленькие числа появляются очень большие числа, и чем меньше мы берем x, тем больше становится 1/x. Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?
Алгебраическое возражение против этого состоит в следующем. Предположим, что ∞=1/x является числом. Тогда на это число должны распространяться все правила, которые имеют место быть для обычных чисел. В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0, а из этого уже следует, что все числа равны между собой и равны нулю. В самом деле, поскольку для любого числа x верно 1⋅x=x, то 1⋅x=0⋅x=0.
«Ну разве это не полная чушь?» — спросим себя, добравшись до этого места.
Разумеется, это полная чушь, если мы говорим об обычных числах. Но я недаром подчеркнул выше слово «правила». К ним мы вернемся чуть позже, после рассмотрения арифметического возражения против деления на ноль, и поможет нам в этом фасоль.
Вернемся в те времена, когда не было ни компьютеров, ни калькуляторов, ни логарифмических линеек, и поставим перед собой задачу разделить некоторое случайное число, например, на 5.
Для этого берем чашу с фасолью, символизирующую натуральный ряд, и высыпаем из нее какое-то количество зерен на разлинованный лист бумаги:

Тем самым, мы установили делимое на нашем бобовом калькуляторе.
Задача состоит в том, чтобы разложить эти зерна на пять рядов. Чтобы не запутаться отмечаем эти ряды, то есть, устанавливаем делитель:

Теперь раскладываем зерна из кучи на пять рядов в столбик. Это значительно дольше, чем на обычном калькуляторе, зато позволяет почувствовать всю прелесть арифметики до изобретения позиционной системы счисления.

Алгоритм завершается, когда мы получаем некоторое прямоугольное число и (возможно) остаток:

В данном примере осталось 2 зерна, а рядов по 5 зерен образовалось 18. Получается, что случайное число было 18⋅5+2=92.
Ясно, что мы можем выполнить этот алгоритм для любого натурального делимого и любого натурального делителя, отличного от нуля; если же делитель равен 0, то этот алгоритм выполнить попросту невозможно.
«Подождите!» — скажет внимательный читатель. — «В рассмотренном примере мы получили остаток 2, что с ним делать?»
Это, на самом деле, очень важное замечание. Вообще говоря, мы не можем делить фасолины, не испортив наш бобовый калькулятор — мало того, что разделить 2 фасолины на 5 одинаковых частей проблематично, даже если мы их раздробим подобающим образом, мы уже не сможем их собрать.
Поэтому достаточно долго люди старались обходиться без дробей. Например, в анонимной арабской рукописи XII века описана следующая задача: «разделить 100 фунтов между 11 человеками». Поскольку 100=11⋅9+1, средневековый математик предлагает сначала раздать каждому по 9 фунтов, а затем обменять оставшийся фунт на яйца, которых, как оказывается по курсу обмена, получается ровно 91. Но 91=11⋅8+3, поэтому арабский ученый предлагает раздать каждому по 8 яиц, а три оставшихся яйца отдать тому, кто производит раздел, или же обменять на соль к яйцам.
Говоря современным математическим языком, деление проводилось в полукольце натуральных чисел. Впрочем, с таким же успехом, используя красную и белую фасоль, мы могли бы определить деление с остатком и в кольце целых чисел — в изложенном алгоритме появились бы дополнительные правила для выбора цветов используемых для вычислений зерен фасоли, но точно так же остались бы бессмысленными операции вида x/0 и 5/2.
Очевидно, что для того, чтобы придать символу 5/2 конкретный смысл, нужно изменить правила игры, и перейти к полю рациональных дробей, пополнив множество целых чисел всевозможными выражениями m/n, где m — целое, а n — натуральное.
Важно заметить, что сделать это можно не единственным способом, однако в классической арифметике рассматривается такое пополнение, в котором символ 1/n означает долю от деления 1 на n, т. е. такое число, для которого верно выражение n⋅1/n=1; при чем доли имеют смысл не при подсчете штучных предметов (например, зерен фасоли), а при измерении величин, которые предполагаются непрерывными (или хотя бы неограниченно делимыми) — длин отрезков, площадей фигур и т. д.
В поле рациональных дробей уже нет смысла рассматривать неполное частное и остатки, так как частное от любого ненулевого делителя является какой-то рациональной дробью. Более того, как и в случае с натуральными числами, мы можем использовать для деления фасоль без изменения алгоритма.
В самом деле, пусть требуется разделить рациональное число α=p/q на β=r/s. Это равносильно выполнению следующих действий:
α:β=p/q:r/s=p⋅s/q⋅r
и задача при любых рациональных α и β свелась к уже известной процедуре деления целых чисел. Это еще раз показывает, что деление на ноль не имеет никакого арифметического смысла.
«Получается, делить на ноль нельзя, даже если очень хочется?» — увы, ответ на этот вопрос положительный: мы не можем определить операцию деления на ноль исходя их естественных потребностей счета и измерений. Правда, есть две лазейки.
Первая: вместо «обычных» чисел (т.е. кольца натуральных и поля рациональных, а также поля действительных чисел, о котором я, кстати, до сих пор не сказал ни слова и расскажу как-нибудь в другой раз) рассмотреть вырожденный случай — тривиальное кольцо {0}, и положить по определению 0/0=0. В этом случае, когда нам говорят: «Все числа равны между собой и равны нулю!» — мы можем сказать невозмутимым тоном: «Ну и что? Это всегда было так».
Вторая: отказаться от некоторых привычных правил умножения. В частности, от аксиомы 0⋅x=0. Говорят, что это возможно (см. http://en.wikipedia.org/wiki/Wheel_theory). Разумеется, этот вариант гораздо интереснее первого, но и он представляет собой такое изменение правил игры, которое сразу выводит нас за рамки классической арифметики.
В заключение этой заметки хочу привести список литературы для тех, кто заинтересовался числовыми системами:
— И.В. Арнольд «Теоретическая арифметика», М, ОГИЗ 1938 — очень подробная и детальная книга, в которой можно найти описания классических числовых систем, включая кватернионы.
— Е. Г. Гонин «Теоретическая арифметика», М, 1959 — эта книга покороче и посовременнее, и тоже очень хороша, хотя не так подробна, как книга И.В. Арнольда.
— С. Феферман «Числовые системы» — классическая монография, местами достаточно сложная; в ней изложены некоторые частные вопросы, которых нет в двух других книгах по теоретической арифметике.
— А. А. Кириллов «Что такое число?» (1993) — небольшая брошюра, рассчитанная на подготовленного читателя.
— Е. Б. Дынкин, В. А. Успенский «Математические беседы» — популярная книга, рассчитанная на школьников. Содержит массу информации и задач по такой «нестандартной» теме, как p-адические числа.