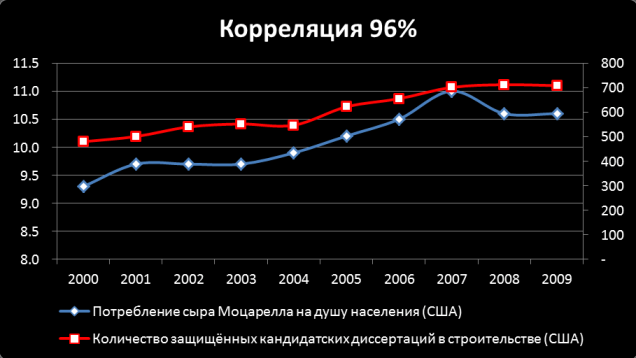
Недавно заметил в ленте фейсбука ссылку на статью с кучей примеров «странных корреляций» как на картинке. Первоисточник оказывается здесь, и там таких примеров штук 20. Решил по-практиковаться в статистике и проверить насколько эти корреляции удивительны на самом деле.
Заинтересованных прошу под кат.
Убираем тренды
Если два показателя всё время растут, то у них будет положительная корреляция, и в этом нет ничего удивительного. Корреляцию нужно мерять по стационарным переменным. Чтобы убрать тренды я построил линейную регрессию от времени по каждому показателю, вычел из фактических данных и проверил корреляцию остатков.
В некоторых случаях корреляция сильно снизилась:
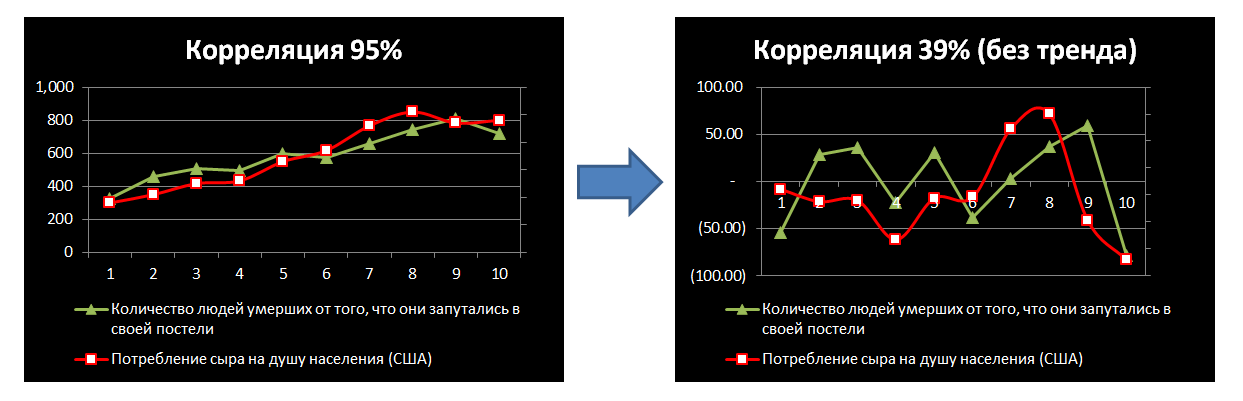
В других – ничего не поменялось:
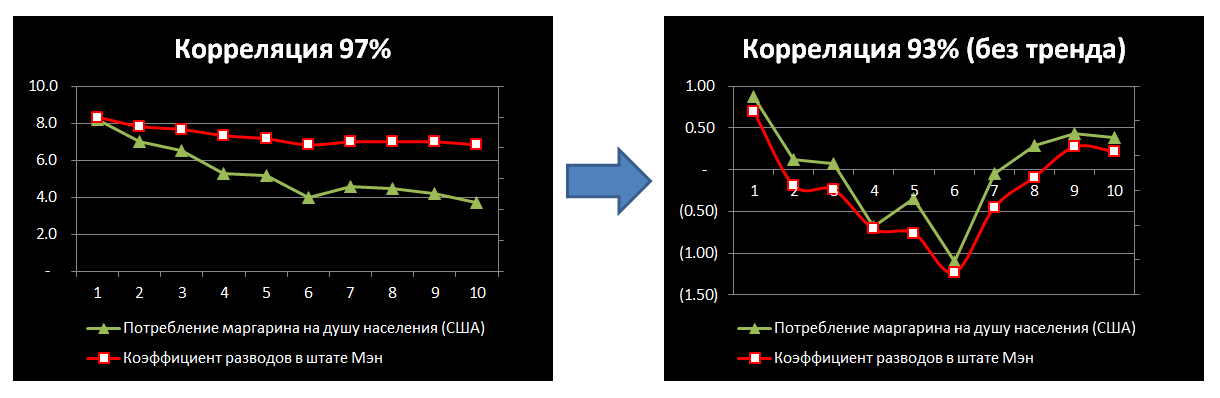
Значит должно быть что-то ещё!
Кстати, я заметил, что положительных корреляций найдено существенно больше, чем отрицательных. Думаю дело в том, что в базе показателей, которые использовал автор, очень много растущих показателей. Люди вообще очень любят измерять что-то растущее. В результате куча показателей, для которых «остатки от тренда» имеют сильную отрицательную корреляцию, оказались не найдены, так как совпадающий положительный тренд сдвигал корреляцию ближе к нулю.
Какая вообще вероятность получить такую корреляцию случайно?
Вот здесь мы возьмёмся за формулы! У меня получилось, что в среднем в этих переменных по 11 точек и после коррекции на тренды средняя корреляция в районе 70%. Зная корреляцию и количество точек можно получить переменную, которая распределена как t-Стьюдента с числом степеней свободы n-2:
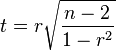
Получаем t=2.98 и вероятность получить такую корреляцию при независимых переменных — порядка 0.77%. Полученная цифра довольно впечатляющая, но вопрос не закрыт!
Причём тут парадокс близнецов?
Вероятность в 0.77% кажется слишком низкой, чтобы верить в случайное совпадение, но интуиция здесь ошибается. Эта ситуация похожа на известный парадокс дней рождения
Вероятность, что два человека родились в один день равна 1/365. Но среди всего 23 человек с 50% вероятностью найдётся пара родившихся в один день. Так происходит, потому что нам не важно какие именно два человека это будут, а среди 23 человек можно составить множество пар.
По же самое происходит и с корреляцией различных показателей, если не важно какие из них будут коррелировать. Две случайных переменных будут сильно коррелировать в одной попытке из 65. Я умножаю вероятность на 2, так как корреляция ниже -70% тоже нас интересует.
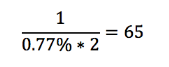
Но если взять всего лишь 9 случайных переменных (по 11 точек в каждой), то с вероятностью 50% там будет корреляция более 70% или менее – 70%
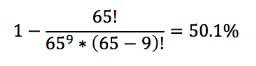
На практике наверняка пришлось просмотреть намного больше переменных. Очень многие показатели на самом деле могут или должны коррелировать и отфильтровать именно «удивительные» было сложно. Но после статистического анализа видно, что и в найденных показателях нет ничего удивительного. Опять интуиция подводит человека в вопросах оценки вероятностей.