
В мае прошлого года сотрудники лаборатории глубокого обучения Гугла и учёные из двух американских университетов опубликовали исследование «Intriguing properties of neural networks». Статья о нём вольно пересказывалась здесь на Хабре, и само исследование также критиковалось специалистом из ABBYY.
Гугловцы в результате своих исследований разочаровались в способностях нейронов сети распутывать признаки входных данных и стали склоняться к мысли, что нейронные сети не распутывают семантически значимые признаки по отдельным структурным элементам, а хранят их во всей сети в целом как в голограмме. В нижней части иллюстрации к этой статье чёрно-белыми я привёл карты активации 29, 31 и 33-его нейронов сети, которую обучил рисовать картинку. То, что тушка птицы без головы и крыльев, изображаемая для примера 29-ым нейроном, покажется людям семантически значимым признаком гугловцы считают всего лишь ошибкой интерпретации наблюдателя.
В статье я на реальном примере постараюсь показать, что и в искусственных нейронных сетях распутанные признаки можно обнаружить. Постараюсь объяснить, почему гугловцы увидели то, что они увидели, а распутанных признаков увидеть не смогли, и покажу, где в сети скрываются семантически значимые признаки. Статья является популярной версией доклада, прочитанного на конференции «Нейроинформатика — 2015» в январе этого года. Наукообразную версию статьи можно будет почитать в материалах конференции.
Вопрос сейчас активно дискутируется как среди интересующихся так и среди профессионалов. Доказательств выдерживающих критики не сумела пока предъявить пока ни одна сторона.
Притом что экспериментаторам с помощью имплантированных в мозг электродов в опытах на людях удавалось обнаружить так называемый «нейрон Дженнифер Энистон» – нейрон, реагирующий только на изображение актрисы. Удавалось поймать и нейрон Люка Скайуокера, и нейрон Элизабет Тейлор. С обнаружением у крыс и летучих мышей «координатных нейронов», «нейронов места» и «нейронов границ», многие окончательно привыкают говорить «нейрон такого-то свойства». Хотя открыватели нейрона Дженифер Энистон, ответственно интерпретируя данные, скорее говорят о том, что обнаружили часть крупных ансамблей нейронов, а не отдельные нейроны признаков. Её нейрон реагировал на связанные с ней понятия (например, сцены из сериала, в которых её нет в кадре), а найденный у человека нейрон Люка Скайуокера срабатывал и на магистра Йоду. Чтобы окончательно всех запутать в одном исследовании – нейроны, реагирующие выборочно на змею, удавалось найти у обезьян, которые змеи никогда в своей жизни не видели.
В общем тема «Нейрона Бабушки», поднятая нейрофизиологами в 1967-69 годах вызывает немалые волнения по сей день.
Часть первая: данные
Чаще всего нейронная сеть используется для классификации. На вход ей подаётся множество входных зашумлённых образов, а на выходе она должна их успешно классифицировать по малому количеству признаков. Например, присутствует ли на картинке кошечка или нет. Эта типовая задачка неудобна для поиска внутри сети осмысленных признаков во входных данных по целому ряду причин. И первая из них в том, что нет возможности строго наблюдать взаимосвязь между семантическим признаком и состоянием какого-нибудь внутреннего элемента. В статье от Гугла и нескольких других исследованиях использовался хитрый трюк – сначала вычислялись входные данные, которые максимально возбудят выбранный нейрон, а затем исследователь внимательно эти данные рассматривал, пытаясь найти в них смысл. Но мы знаем, что человеческий мозг умеет мастерски находить смысл даже там, где его нет. Мозг долго эволюционировал в этом направлении, и то, что на тесте Роршаха люди видят что-то кроме кляксы чернил на бумаге, заставляет с большой осторожностью относиться к любым методам поиска смысла на картинке содержащей много элементов. В том числе и на моих картинках.
Метод, используемый в этом и ряде других исследований плох ещё и тем, что нормальным режимом работы нейрона вообще может быть не максимальное возбуждение. Например, на средней картинке, где изображена карта активации 31-ого нейрона, видно, что на корректных входных данных до максимального значения он не возбуждается, да и вообще при взгляде на картинку кажется, что смысл, скорее, несут области, где он не активен. Чтобы увидеть что-то настоящее может оказаться полезным изучать поведение сети в малых окрестностях от её нормального рабочего режима.
Кроме того, в Гугловском исследовании исследовались очень большие сети. Сети для обучения без учителя содержали до миллиарда изменяемых параметров, например. Даже если в сети будет нейрон, большими чёрными буквами выписывающий слово «экзистенция» случайно наткнуться на него оказалось бы очень трудно.
Поэтому мы будем экспериментировать с совсем другой задачей. Сначала экспериментатор загадывает картинку. У сети всего два входа, и на них подаются два действительных числа – координаты X и Y. А на трёх выходах R, G и B мы будем ожидать предсказание, какого цвета точка должна находиться на картинке в этих координатах. Все величины отнормированы на отрезок (-1; 1). Среднеквадратичная ошибка по всем точкам картинки в сумме станет критерием успешности обучения рисованию (на некоторых картинках пишется в левом нижнем углу, RMSE).
В статье используется нерекуррентная сеть из 37 нейронов с гипертангенсом в качестве сигмоиды и несколько нестандартным расположением синапсов. Для обучения использовался метод обратного распространения ошибки, с версией Mini-Batch алгоритма, и дополнительным алгоритмом, являющимся дальним родственником алгоритмам ограничения энергии. В общем и целом ничего сверхъестественного. Бывают и более современные алгоритмы, но большинство из них не способны на сети такого скромного размера добиться более точных результатов.
А теперь заполним картинку пикселями, окрашенными так, как предсказывает наша сеть. Получится карта представлений нейронной сети о прекрасном, использованная в начале статьи в качестве картинки для привлечения внимания. Слева исходная картинка летящего павлина, а справа то, как её представила себе нейронная сеть.
Первый важный вывод можно сделать с первого же взгляда на картинку. Не очень осмысленно будет надеяться, что признаки изображения описываются нейронами. Хотя бы потому, что на картинке явно различимых элементов изображений попросту больше чем нейронов. То есть, авторы большинства исследований, ищущие признаки в нейронах, ищут не там.
Часть вторая: Немножко реверс-инжиниринга
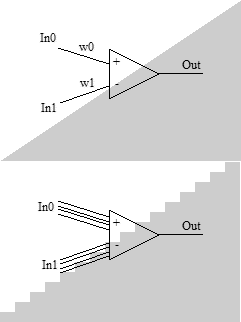 Представим, что перед нами и поставили задачу: безо всякого обучения сконструировать из нейронов классификатор, определяющий, где находится входная точка – выше или ниже прямой, проходящей через точку (0,0). Для решения такой задачи достаточно одного нейрона. Веса синапсов соотносятся как коэффициент наклона прямой и имеют разные знаки. Знак потенциала на выходе даст нам ответ.
Представим, что перед нами и поставили задачу: безо всякого обучения сконструировать из нейронов классификатор, определяющий, где находится входная точка – выше или ниже прямой, проходящей через точку (0,0). Для решения такой задачи достаточно одного нейрона. Веса синапсов соотносятся как коэффициент наклона прямой и имеют разные знаки. Знак потенциала на выходе даст нам ответ.Теперь существенно усложним задачку. Будем точно так же сравнивать две величины, но теперь входные значения будут поступать в виде двоичного числа. Например, 4-битного. С такой задачей, кстати, справится уже очень не каждый алгоритм обучения. Тем не менее, аналитический ответ тоже очевиден. Обходимся всё тем же одним нейроном. У первой четвёрки синапсов, принимающих первую величину, веса соотносятся как 8:4:2:1, у второй – то же самое, но отличающееся в -k раз. Разнести решение этой задачи в два отдельных нейрона значит усложнить решение задачи, если только входное значение, преобразованное из двоичного кода, не необходимо где-то ещё в другой части сети. И что же получается: с одной стороны, нейрон один, но, с другой стороны, у него обнаруживается два совершенно отдельных ансамбля синапсов представляющих обработку разных свойств входных данных. Отсюда следует первый вывод:
- За представление свойств в нейронной сети могут отвечать не нейроны, а группы синапсов.
- В одном нейроне мы часто видим комбинацию нескольких признаков.
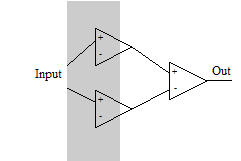 Проделаем третий мысленный эксперимент. Пусть у нас есть всего один вход и нам необходимо, чтобы нейрон включался только на одном диапазоне значений. Такую задачу решить на одном нейроне с монотонной функцией активации не получится. Нам потребуется три нейрона. Первый будет активироваться на первой границе и активировать выходной нейрон, второй – активироваться при большем входном значении и тормозить выходной нейрон на второй границе.
Проделаем третий мысленный эксперимент. Пусть у нас есть всего один вход и нам необходимо, чтобы нейрон включался только на одном диапазоне значений. Такую задачу решить на одном нейроне с монотонной функцией активации не получится. Нам потребуется три нейрона. Первый будет активироваться на первой границе и активировать выходной нейрон, второй – активироваться при большем входном значении и тормозить выходной нейрон на второй границе.Этот мысленный эксперимент учит нас новым важным выводам:
- Ансамбль синапсов может захватывать несколько нейронов.
- Если в системе есть несколько синапсов, меняющих некоторую границу с разной интенсивностью и в разный момент, ансамбль синапсов, включающий их оба может использоваться для того чтобы управлять новым свойством «промежуток между границами».
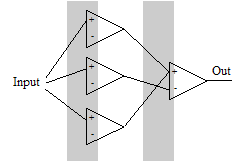 Наконец поставим последний четвёртый мысленный эксперимент.
Наконец поставим последний четвёртый мысленный эксперимент.Допустим, нам требуется включать выходной нейрон на двух независимых и неперекрывающихся участках. Решить задачку можно, пользуясь 4 нейронами. Первый нейрон активируется и активирует выходной. Второй нейрон активируется частично и тормозит выходной нейрон. В это время активируется третий, вновь активируя выходной нейрон. Наконец, второй нейрон набирает максимальную активацию и за счёт большего веса своего синапса вновь тормозит выходной нейрон. Тогда 1-ая граница почти полностью зависит от первого нейрона, а четвёртая – от последнего в первом слое. Однако положение второй и третьей границ хоть и можно изменить, не затрагивая других границ, но для этого придётся менять веса нескольких синапсов согласованно. Этот мысленный эксперимент научил нас ещё нескольким принципам.
Несмотря на то, что каждый синапс в сети такого типа влияет на обработку всего сигнала, но только немногие из них влияют на отдельные свойства сильно, обеспечивая их представление и изменение. Воздействие большинства синапсов оказывается существенно менее сильным. Если пытаться повлиять на свойство, меняя такие «слабые» синапсы, то те свойства, в управление которыми они вовлечены сильно, изменятся неприемлемо гораздо раньше чем вы заметите какие либо изменения в выбранном признаке.
- Некоторые синапсы составляют ансамбли, способные изменять отдельные признаки. Ансамбль работает только в рамках существующего около него окружения других нейронов и синапсов. При этом работа ансамбля почти не зависит от малых изменений окружения.
Вот такие ансамбли синапсов, характеризующиеся описанными свойствами, мы и будем искать в нашей сети, чтобы подтвердить возможность их существования на реальном примере.
Часть третья: Синаптические ансамбли
Малые размеры сети, заданные нами в первой части статьи, дают нам возможность непосредственно изучить, как изменение веса каждого из синапсов влияет на картинку, порождаемую сетью. Начнём с самого первого синапса, строго говоря, номера 0. Этот синапс в гордом одиночестве отвечает за наклон тушки птицы в левую сторону, и ни за что кроме. Никакой другой синапс не принимает участия в формировании этой опорной линии.

На картинке показано очень большое изменение веса синапса, с -0.8 до +0.3, специально, чтобы вызываемое изменение было более заметным. При таком большом изменении веса синапса начинают меняться уже и другие свойства. В реальности рабочий диапазон изменений веса данного синапса гораздо меньше.

Взглянув на карту активации нейрона, к которому ведёт этот синапс, можно подумать, что второй синапс этого нейрона тоже будет как-то управлять наклоном первой опорной линии, вокруг которой строится вся геометрия нашей птички, но нет. Изменения веса второго синапса приводит к изменению другого свойства — ширины тела птицы.

Здесь надо отметить, что воздействие близко расположенных синапсов на свойство часто можно интерпретировать как отдельное свойство. Однако в общем случае это неверно. Например, посмотрим на карту изменений, вызываемых 418-ым синапсом, являющимся частью ансамбля, контролирующего баланс зелёного на картинке.

Если мы попытаемся двигать сеть вдоль базиса, состоящего из 0-ого и 418-ого синапсов мы увидим, как птичка наклоняется влево и становится всё менее зелёной, но считать это одним свойством вряд ли возможно. В своей статье гугловцы утверждали, что натуральный базис, максимально возбуждающий один структурный элемент сети, по кажущейся семантической значимости не хуже базиса, собранного из линейной комбинации таких векторов для нескольких элементов. Но мы видим, что это верно только когда синапсы, вдоль которых происходит наибольшее изменение, входят в близкие синаптические ансамбли. Но если синапсы регулируют сильно разные свойства, то смешение не помогает в них запутаться.

Теперь рассмотрим какое-нибудь более сложное свойство, затрагивающее малую часть картинки. Например, размеры и форму областей под крыльями, где у нашего павлина короткие хвостовые перья. Выпишем все нейроны, которые влияют на эти области напрямую (например, на левую из них), а именно, отвечают за изменение отдельных частей птицы, а не её общей геометрии. Получится, что в ансамбль входят синапсы 21,22, 23, 24, 25, 26, 27.

К примеру, 23-ий и 24-ый синапсы, увеличивают выбранную нами область, противоположным образом влияя на длину крыла. Так что, изменяя их одновременно можно менять область, под крылом мало влияя на длину крыла. В точности как в предложенном нами четвёртом мысленном эксперименте.

Все эти синапсы ведут к 6-ому нейрону, и при взгляде на его карту активации, мягко говоря, не очевидно, что он участвует в контроле этого свойства. Что говорит в пользу эффективности предложенного в данной статье способа визуализации.

Если мы посмотрим, какие синапсы влияют на размер и форму этой области совместно с другими областями то наберётся ещё пара дюжин 37-46 (8-ой нейрон), 70-83(11 и 12-ый нейроны), 90-94(12 и 13-ый нейроны), 129-138 (16-ый нейрон) и ещё несколько, например 178-ой (19-ый нейрон). В общей сложности в ансамбль вовлечено ~46 синапсов из 460 имеющихся в сети. При этом остальные синапсы могут изгибать почти всё изображение, но выбранной области почти не затрагивают, как например 28-ой, даже если за него очень сильно подёргать.

Итак, что мы видим? Ансамбль синапсов, регулирующий выбранное нами свойство. Его влияние на другие свойства сеть при необходимости компенсирует согласованным изменением весов синапсов в ансамбле или задействовав другие ансамбли. Ансамбль синапсов задействует по меньшей мере 7 нейронов, это пятая часть всех нейронов сети и они также используются многими другими ансамблями.
Точно также можно подробно рассмотреть синапсы влияющие на цвет областей, или форму маховых перьев. На многие другие признаки присутствующие на изображении.
Часть четвёртая: Анализ результатов
Элементы сети, кодирующие семантически значимые признаки, в сети могут быть, но это не нейроны, а ансамбли синапсов разного размера.
Большинство нейронов участвуют сразу в нескольких ансамблях. Поэтому, изучая параметры активации отдельного нейрона, мы будем видеть комбинацию влияния этих ансамблей. Это с одной стороны сильно затрудняет определение роли нейронов, а с другой большинство комбинаций ансамблей покажется исследователю если и не буквально осмысленной, то содержащей явные признаки смысла.
В исследовании Гугловцев, которое упоминалось в самом начале, конечно же, не утверждалось прямо, что структурные единицы сети не кодируют семантически значимые признаки. Доказать несуществование вообще крайне трудно. Вместо этого они сравнивали данные, которые активировали один случайный нейрон и данные активирующие линейную комбинацию нескольких случайно выбранных нейронов одного слоя. Они показали, что степень кажущейся осмысленности таких данных не различается и трактовали это как указание, на то, что отдельные признаки не кодируются.
Однако теперь глядя на материал статьи мы понимаем, что и один нейрон, как и линейная комбинациях нескольких близких нейронов демонстрируют ответ на данные нескольких ансамблей синапсов, и действительно по содержанию информации отличаются не принципиально. То есть наблюдение, сделанное в исследовании верное, и его можно было ожидать, под сомнением только его интерпретация, данная в самых общих словах.
Также становятся понятным, почему разные работы по теме выделения семантически значимых признаков в структурных элементах сети давали на столько различные результаты.
В заключении хочу совсем мельком сказать о том, с чего начал. О картах активации последних нейронов в сети, так красноречиво выглядящих. Нейронная сеть может приближаться к требующейся от неё функции в виде суммы функций эффективно аппроксимирующих отдельные участки. Но чем больше данных успешно выучивает сеть, тем меньше она может выделить своих структурных элементов на то, чтобы кодировать каждый отдельный признак. Тем больше она вынуждена искать и применять качественные обобщения. Если нужно осуществить простую классификацию имея миллиард настраиваемых параметров каждый из них, скорее всего, будет управлять свойством только на одном маленьком участочке и только вместе с сотнями других таких же. Однако если сеть заставить выучить картинку, в которой под сотню значимых свойств, а нейронов у неё в распоряжении всего под четыре десятка, она или не справится или выделит семантически значимые признаки в отдельные структурные единицы, где их будет легко обнаружить. Выходные нейроны сети связаны с не очень большим количеством нейронов, и для формирования картинки с таким большим количеством значимых элементов, сети пришлось на предпоследних нейронах собирать результаты работы нескольких ансамблей синапсов вместе. Нейронам 29, 31 и 33 повезло, в них собрались геометрические данные, которые легко распознать и мы сразу обратили на них внимание. Нейронам 27, 28 или 32 повезло меньше, в них собралась информация о расположении цветовых пятен на картинке и понять что эта какофония означает сможет только сама нейронная сеть.
