Содержание основного курса
- Статья 1: алгоритм Брезенхэма
- Статья 2: растеризация треугольника + отсечение задних граней
- Статья 3: Удаление невидимых поверхностей: z-буфер
- Статья 4: Необходимая геометрия: фестиваль матриц
- Статья 5: Пишем шейдеры под нашу библиотеку
- Статья 6: Чуть больше, чем просто шейдер: просчёт теней
- Статья 3.1: Настала пора рефакторинга
- Статья 3.14: Красивый класс матриц
- как работает новый растеризатор
Общение вне хабра
Если у вас есть вопросы, и вы не хотите задавать их в комментариях, или просто не имеете возможности писать в комментарии, присоединяйтесь к jabber-конференции 3d@conference.sudouser.ru4 Приветствие и вступление
Нумерация в прошлой статье закончилась на 3, в этой будем продолжать нумеровать насквозь.UPD: ВНИМАНИЕ! Раздел, начиная с номера 3.1, 3.14 и 3.141 и далее, будет о тонкостях реализации основы основ компьютерной графики — линейной алгебры и вычислительной геометрии. О принципах графики пишет haqreu, я же буду писать о том, как это можно внятно запрограммировать!
Эта статья является продолжением серии статей о практической реализации элементов вычислительной геометрии, и, в частности, программного отрисовщика, с использованием C++98. Мы с haqreu сознательно идем на использование прошлой версии стандарта и написание собственной геометрической библиотеки для того, чтобы, во-первых, выпустить код примеров, которые без особых трудностей будут компилироваться большинством имеющихся компиляторов, а во-вторых, чтобы в нашем коде не было ничего, что скрыто в недрах библиотеки. В статье излагаются вопросы реализации шаблона прямоугольной матрицы
template<size_t DimRows,size_t DimCols,typename number_t> class mat;4.1 Благодарности
Я выражаю огромную признательность haqreu, как основоположнику данного курса. Так держать!Я очень признателен lemelisk за предварительное рецензирование и ревью моих исходников. Спасибо за плодотворные дискуссии!
Также я должен поблагодарить Mingun за ценное замечание об оформлении шаблонов. Надеюсь, они стали доступнее для прочтения.
4.2 Небольшое философское замечание о языке, математике, C++, и всем таком
В целом, такие абстракции, как «матрица» и «вектор» и операции над ними необходимы для того, чтобы упростить и формализовать язык изложения геометрии. Без них нам приходилось бы постоянно говорить (и писать в программе) что-то вроде:Говорим:
Чтобы получить новые координаты точки Point, которая перемещена в направлении Direction, нужно сложитьПишем:
x точки Point с x перемещения Direction,
у точки Point с y перемещения Direction,
z точки Point с z перемещения Direction
Point.x=Point.x+Direction.x;
Point.y=Point.y+Direction.y;
Point.z=Point.x+Direction.z; //(Привет, "Эффект последней строки")
После того, как понятие «вектор» вошло в наш речевой оборот, мы уже можем говорить:
Чтобы получить новый радиус-вектор точки Point после перемещения в направлении Direction, нужно сложить векторы Point и Direction
А после включения в наш код шаблона vec, мы можем писать:
Point=Point+Direction;
Вот что об этом пишет Джефф Элджер в книге «C++ for Real programmers», (издательство AP Professional, перевод выпущен издательством «Питер» под названием «C++: Библиотека программиста»)
С++ —это на самом деле не столько язык, сколько инструмент для создания ваших собственных языков. Его элегантность заключается отнюдь не в простоте (слова С++ и простота режут слух своим явным противоречием), а в его потенциальных возможностях. За каждой уродливой проблемой прячется какая-нибудь умная идиома, изящный языковой финт, благодаря которому проблема тает прямо на глазах. Проблема решается так же элегантно, как это сделал бы настоящий язык типа Smalltalk или Lisp, но при этом ваш процессор не дымится от напряжения, а на Уолл-Стрит не растут акции производителей чипов памяти
Как раз этим мы и займемся — будем строить с использованием C++ язык управления геометрическими примитивами, стараясь делать это как можно ближе к определениям из математики.
5 Шаблон класса для обработки и хранения матриц
Мы храним матрицу как массив вектор-строк, используя соответствующую специализацию шаблона vec. Наш шаблон ориентирован только на работу с матрицами малой размерности (максимум 10x10 элементов. Хотя это уже будет ужас). Но в вычислительной геометрии, как правило, вся работа идет именно с матрицами не больше, чем 4x4. Большие же матрицы получаются, как правило, очень разреженными — для них заранее известно, что они практически полностью заполнены нулями, что позволяет оптимизировать их обработку и хранение.5.1 Индексные операторы
Мы определили константный и неконстантный варианты индексного оператора [] таким образом, чтобы они возвращали ссылку на соответствующую вектор-строку матрицы:их исходные тексты
Два варианта операторов нужны из-за того, что мы везде, где только возможно, применяем | Константный вариант |
Неконстантный вариант |
|
|
const. Если бы не было константного варианта индексного оператора, компилятор не позволял бы нам собрать код, в котором, например, оператор вызывается по константной ссылке на экземпляр матрицы:Так ругается GCC 4.9.2, когда не находит константного варианта оператора []
Кроме того, мы здесь применяем макрос geometry.h:182: ошибка: no match for 'operator[]' (operand types are 'const mat<2ul, 3ul, float>' and 'size_t {aka long unsigned int}')
for (size_t i=DimRows; i--; ret[i]=lhs[i]*rhs);
^
assert() для отлова попыток обратиться к несуществующей строке матрицы. Подробнее про assert написано в статье 3.15.2 Вычисление обратной матрицы
Нам потребовалась подпрограмма для вычисления обратной матрицы. В частности, используя обратную матрицу можно «красиво» находить барицентрические координаты (можно посмотреть в моей ветке на гитхабе, функцияfilltria). Задача вычисления обратной матрицы в общем случае является достаточно затратной по времени и может сопровождаться накоплением значительной погрешности при вычислениях. Однако для столь малых матриц эти проблемы не так существенны (если не строить такой пример специально). Мы выбрали алгоритм с применением союзной матрицы, потому как он показался нам более прозрачным, нежели алгоритм Гаусса-Жордана. Используется следующий факт:
- если для данной матрицы составить союзную матрицу,
- а затем транспонировать
- и поделить ее на определитель данной,
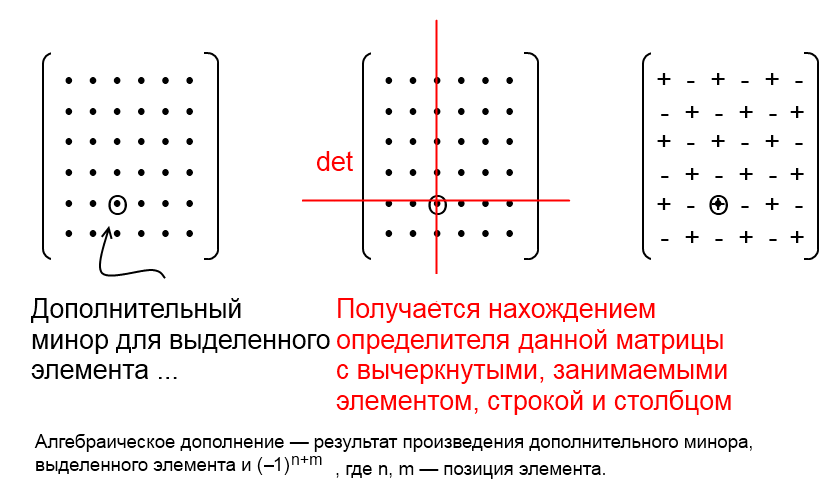
Союзная же матрица составляется из алгебраических дополнений. Алгебраическое дополнение — это определитель подматрицы, полученной из основной путем удаления строки и столбца, содержащих элемент, для которого мы находим это дополнение.
Получили следующий вопрос — как найти определитель.
Используем такое свойство:
определитель равен произведению элементов строки или столбца матрицы на их алгебраические дополнения.
Получилась рекурсия — алгебраическое дополнение — тоже определитель матрицы, только размерность на единицу меньше. А определитель матрицы размерности 1 — это ее единственный элемент. Рекурсия замкнулась. Мы воспользуемся прекрасной особенностью шаблонов C++ — развернем эту рекурсию прямо во время компиляции.
Замечание: Матрица у нас — прямоугольная, а определитель можно вычислить только для квадратной матрицы. Хотелось бы уже на этапе компиляции отлавливать попытки найти определитель неквадратной матрицы. Есть два способа это сделать:
- унаследовать от mat класс squareMat, в котором объявить определитель
- воспользоваться тем, что размеры матрицы нам известны еще на этапе компиляции, поэтому мы можем их сравнить и прервать компиляцию, если они не совпали
В первом случае мы получим отдельный тип матриц и кучу проблем с преобразованием матриц туда-сюда, потому как у нас может образоваться квадратная матрица в рамках типа mat, но чтобы посчитать определитель, нам придется конструировать из нее экземпляр типа squareMat.
Поэтому мы выберем второй способ — при разворачивании шаблонов обнаруживать несовпадение размеров и ломать компиляцию. В С++11 есть стандартное средство это сделать — static_assert(). В С++98 такого средства нет, поэтому мы изобретем суррогатное:
template<bool>
struct static_assertion;
template<>
struct static_assertion<true> {};
geometry.h:125: ошибка: invalid use of incomplete type 'struct static_assertion<false>'
static_assertion<DimCols<=10>();
^
Вернемся к нашей рекурсии:
Исходные тексты шаблона, отвечающего за рекурсию
///////////////////////////////////////////// полный шаблон структуры dt
1. template<size_t Dim,typename number_t> struct dt
2. {
3. static number_t det(const mat<Dim,Dim,number_t>& src)
4. {
5. number_t ret=0;
6. for (size_t i=Dim; i--;)
7. {
8. ret += src[0][i] * src.cofactor(0,i);
9. }
10. return ret;
11. }
12. };
///////////////////////////////////////////// частичная специализация шаблона для случая, когда размерность равна 1.
13. template<typename number_t> struct dt<1,number_t>
14. {
15. static number_t det(const mat<1,1,number_t>& src)
16. {
17. return src[0][0];
18. }
19. };
Итак, для всех ситуаций, когда первый параметр шаблона не равен 1, будет применяться верхний шаблон (строки 1-11). Для ситуации, первый параметр равен 1, определена специальная версия шаблона (строки 12-18). Обратите внимание на строку 13: Дополнение
<1,number_t> как раз и указывает, что это объявление — отдельная сущность. С общей версией шаблона dt ее ничего не связывает. Встречается ошибка, когда путают поведение частичной специализации и наследования, ожидая, что все объявленное в общей версии окажется и в частичной. Этого не будет — на программиста возлагается воссоздание в частичной специализации всего, что ему нужно.- Оборачивание в отдельную структуру выполнено потому, что стандарт не разрешает делать частичную специализацию для функций.
- Мы вынесли эту функцию из mat потому, что поступив иначе, были бы вынуждены дописывать в mat<1,1,number_t> часть методов из общей версии, что привело бы к некоторому раздутию кода.
Общая же версия шаблона выполняет разложение матрицы по нулевой строке — она берет элемент с индексом
0, i из первой строки, умножает его на алгебраическое дополнение — cofactor(0,i) а результат накапливает в переменной ret. Все в полном согласии с формулой этого разложения:5.3 Как происходит рекурсия
ВАЖНО: Строго говоря, механизм обработки шаблонов — личное дело компилятора. Ниже я рассказываю о том, как это могло бы происходить. Это делается только для иллюстрации того, как рекурсивно разворачиваются декларации шаблонов.Представим, что мы самостоятельно выполняем разворачивание шаблонов. Написан код:
...
using namespace std;
int main()
{
mat<3,3,int> m;
....
cout << m.det() << endl;
return 0;
}
| Шаблон |
Результат подстановки DimCols=3; DimRows=3; number_t=int |
|
|
| Шаблон |
Результат подстановки Dim=3; number_t=int |
|
|
| Шаблон |
Результат подстановки DimCols=3; DimRows=3; number_t=int |
|
|
| Шаблон |
Результат подстановки DimCols=3; DimRows=3; number_t=int |
|
|
Методы, появившиеся при разворачивании шаблона 2x2
Мы должны получить текст функции det() для конкретного случая mat<2,2,int>:
Отлично, теперь нам нужно из шаблона template<size_t Dim,typename number_t> struct dt получить конкретный текст для случая dt<2,int>:
Мы встретили вызов оператора [] и cofactor() из mat<2,2,int>. Тело [] сейчас для нас интереса не представляет, разбираемся с cofactor():
Здесь вызывается get_minor(). Получим для нее текст:
| Шаблон |
Результат подстановки Dim=2; number_t=int |
|
|
| Шаблон |
Результат подстановки Dim=2; number_t=int |
|
|
| Шаблон |
Результат подстановки DimCols=2; DimRows=2; number_t=int |
|
|
| Шаблон |
Результат подстановки DimCols=2; DimRows=2; number_t=int |
|
|
Развернув цепочку шаблонов, мы снова столкнулись с вызовом get_minor() в теле cofactor(), но уже для случая DimCols=2, DimRows=2. Полученная версия get_minor() возвращает матрицу 1x1. Далее, для нее в теле cofactor() запрашивается определитель. Мы снова должны получить текст mat::det(), но уже для случая DimCols=1; DimRows=1.
| Шаблон |
Результат подстановки DimCols=1; DimRows=1; number_t=int |
|
|
| Шаблон |
Результат подстановки Dim=1; number_t=int |
|
|
Видим, что здесь уже нет обращения к cofactor(). На этом раскрутка рекурсии закончена — мы получили тела функций для вычисления определителя матриц 3x3, 2x2, 1x1.
Важное замечание: Может возникнуть желание написать так:
number_t det()
{
if(DimCols==1 && DimRows==1)
{
return rows[0][0];
}
number_t ret=0;
for (size_t i=DimCols; i--;)
{
ret += src[0][i] * src.cofactor(0,i);
}
return ret;
}
Мотивация простая — это будет вроде как обычная рекурсия, да и частичная специализация не нужна. Однако во время развертывания шаблонов, компилятор ничего не будет делать с условным оператором, а начнет строить шаблоны(3, 2, 1, 0, std::numeric_limits<size_t>::max, std::numeric_limits<size_t>::max-1, ...), пока его не остановит внутренний счетчик
-ftemplate-depth=(по умолчанию, эта глубина погружения равна 900).Возможность использовать привычные операторы управления потоком появляется в C++11 для функций, объявленных c ключевым словом
constexpr. Они позволяют организовать еще один вид вычислений во время компиляции, отличный от рекурсии на шаблонах. А не провернуть ли мне весь наш рендер во время компиляции?Итак, мы описали в терминах C++ отыскание определителя матрицы, а также сопутствующие этому операции — построение минора матрицы и алгебраического дополнения. Для отыскания обратной матрицы осталось только построить союзную матрицу:
Метод, строящий союзную матрицу:
действует точно по определению — заполняет матрицу алгебраическими дополнениями соответствующих элементов.mat<DimRows,DimCols,number_t> adjugate() const
{
mat<DimRows,DimCols,number_t> ret;
for (size_t i=DimRows; i--;)
{
for (size_t j=DimCols; j--;)
{
ret[i][j]=cofactor(i,j)
}
}
return ret;
}
Осталось выполнить главный этап построений — найти обратную матрицу (она будет получена в транспонированном виде):
mat<DimRows,DimCols,number_t> invert_transpose()
{
mat<DimRows,DimCols,number_t> ret = adjugate(); //получили союзную матрицу
number_t det = ret[0]*rows[0]; //вычислили определитель исходной матрицы, путем скалярного
//умножения первой вектор-строки
//элементов на вектор строку их алгебраических дополнений
return ret/det; //поделили союзную матрицу на определитель исходной,
//получив тем самым транспонированную обратную матрицу
}
5.4 Умножение матриц
Операция перемножения матриц также довольно затратна по времени и может сопровождаться накоплением погрешности. В случаях матриц большей размерности (больше, чем 64x64), как правило, применяют специальные алгоритмы, вроде алгоритма Штрассена. Асимптотический рекордсмен — Алгоритм Копперсмита-Винограда (с улучшениями Вирджинии Вильямс), сейчас не применяется, потому как начинает обгонять алгоритм Штрассена на матрицах настолько огромных, что в современной вычислительной практике еще не встречаются. У нас матрицы мелкие, поэтому нам для умножения подходит просто определение операции умножения матриц:Произведение матриц AB состоит из всех возможных комбинаций скалярных произведений вектор-строк матрицы A и вектор-столбцов матрицы B
Сведения об авторе картинки
«Matrix multiplication diagram 2» участника File:Matrix multiplication diagram.svg:User:BilouСм. ниже — Этот файл является производной работой от: Matrix multiplication diagram.svg. Под лицензией CC BY-SA 3.0 с сайта Викисклада.
Определение в таком виде позволяет нам использовать операцию скалярного умножения из нашего шаблона vec. Но для этого нам нужен метод, извлекающий из матрицы ее столбец в виде вектора:
текст метода col()
Да, здесь вроде как имеет место быть лишнее копирование (позже мы посмотрим, справится ли компилятор с его выбрасыванием), но главная цель — написать такое краткое и емкое умножение матриц:vec<DimRows,number_t> col(const size_t idx) const
{
assert(idx<DimCols);
vec<DimRows,number_t> ret;
for (size_t i=DimRows; i--;)
{
ret[i]=rows[i][idx];
}
return ret;
}
template<size_t R1,size_t C1,size_t C2,typename number_t>
mat<R1,C2,number_t> operator*(
const mat<R1,C1,number_t>& lhs,
const mat<C1,C2,number_t>& rhs
)
{
mat<R1,C2,number_t> result;
for (size_t i=R1; i--; )
{
for (size_t j=C2; j--;)
{
result[i][j]=lhs[i]*rhs.col(j); //перемножить скалярно i-тую строку левого операнда
// на j-тый столбец правого
}
}
return result;
}
Уделим внимание этому тексту. Здесь на C++ изложено математическое определение операции умножения прямоугольных матриц, причем сделано это очень близко к тексту[«заполнение матрицы-результата всевозможными скалярными произведениями вектор-строк левой матрицы на вектор-столбцы правой»].
При этом контроль размерностей (число столбцов левой должно быть равно числу строк правой) выполняется сразу на этапе компиляции — попытка перемножить не подходящие по размеру матрицы даже не откомпилируется.
А это очень важно, ведь ошибка времени выполнения может быть плавающей, трудноуловимой и так далее. А ошибка компиляции вылезает практически всегда. (Нужно учесть сумасшествие IDE, которая может часть проекта закэшировать, часть забыть обновить и так далее. Но от этого есть верное лекарство — Rebuild All).
5.5 Генератор единичных матриц
В его тексте:static mat<DimRows,DimCols,number_t> identity()
{
mat<DimRows,DimCols,number_t> ret;
for (size_t i=DimRows; i--; )
{
for (size_t j=DimCols;j--;)
{
ret[i][j]=(i==j) ;
}
}
return ret;
}
Есть интересная особенность — запись результата типа bool в переменную априорно неизвестного типа number_t. Здесь может случиться кошмарик у человека, который захотел бы использовать нашу геометрию в своем проекте, причем вместе с самодельным типом для хранения чисел (это может быть тип, который хранит числа с фиксированной запятой). Он может не ожидать, что наши методы будут пытаться записывать в его тип значения bool (оператор == для size_t возвращает bool), и нагородить собственный конструктор, принимающий bool и делающий это преобразование не так, как описано в стандарте ([§4.7/4] требует, чтобы при приведении bool в числовой тип, false превращалось в 0, true — в 1). Так как в данном случае, от стандарта отступает гипотетический пользователь, нам не следует пытаться подстилать ему соломку (мы могли бы сотворить такое:
ret[i][j]=static_cast<number_t>(static_cast<int>(i==j)), и передавать ему хотя бы int) ценой череды преобразований — нарушил стандарт — сам виноват.5.6 Умножение матрицы на вектор
Для умножения матрицы (слева) на вектор (справа), мы рассмотрим вектор как матрицу из одного столбца. Далее, мы можем выполнить уже известную нам операцию умножения матриц, которая в итоге также даст матрицу из одного столбца — этот вектор-столбец и будет результатом умножения.Нам понадобится метод set_col() для заполнения столбца матрицы из вектора:
void set_col(size_t idx, vec<DimRows,number_t> v)
{
assert(idx<DimCols);
for (size_t i=DimRows; i--;)
{
rows[i][idx]=v[i];
}
}
И генератор матрицы по заданному вектор-столбцу
static mat<DimRows,1,number_t> make_from_vec_col(const vec<DimRows,number_t>& v)
{
static_assertion<DimCols==1>();
mat<DimRows,1,number_t> ret;
ret.set_col(0,v);
return ret;
}
Теперь мы можем записать оператор умножения матрицы на вектор:
template<size_t DimRows,size_t DimCols,typename number_t>
vec<DimRows,number_t> operator*(
const mat<DimRows,DimCols,number_t>& lhs,
const vec<DimCols,number_t>& rhs
)
{
return (lhs * mat<DimCols,1,number_t>::make_from_vec_col(rhs) ).col(0);
}
5.7 Деление матрицы на скаляр, вывод в ostream
Выполняются с использованием того факта, что матрица у нас хранится как массив вектор — строк, а для вектора аналогичные операции уже написаны:Тексты операций
template<size_t DimRows,size_t DimCols,typename number_t>
mat<DimCols,DimRows,number_t> operator/(
mat<DimRows,DimCols,number_t> lhs,
const number_t& rhs
)
{
for (size_t i=DimRows; i--; )
{
lhs[i]=lhs[i]/rhs;
}
return lhs;
}
template <size_t DimRows,size_t DimCols,class number_t>
std::ostream& operator<<( std::ostream& out,
const mat<DimRows,DimCols,number_t>& m
)
{
for (size_t i=0; i<DimRows; i++)
{
out << m[i] << std::endl;
}
return out;
}