Предисловие от переводчика
Здесь представлен один из новейших методов расчёта ориентации в пространстве по показаниям датчиков акселерометра, гироскопа и компаса — фильтр Маджвика, который, по словам автора, даёт результат лучший, чем применение фильтра на основе метода Калмана в результатах и производительности. Автор — Себастьян Маджвик (его интернет-магазин). Метод описан в статье на английском. Данная работа защищена в Университете г. Бристоля Перевода я не нашёл. Переводчик из меня так себе, особенно таких сложных текстов. Но нам же интересно, что за метод?
Кое-где буду от себя добавлять — там текст выделен курсивом. Мною найдено более 10 опечаток в оригинальном тексте. Вообще было довольно трудно, поэтому помощь приветствуется — пишите в комментариях, где перефразировать нужно, в общем, где что не так.

Фильтр массивов данных инерционных и инерционно-магнитных датчиков для определения ориентации
30 апреля 2010
От автора
Данная статья описывает новый фильтр показаний датчиков для определения ориентации в пространстве в двух вариантах. Первый вариант применим к инерционным навигационным системам (ИНС), включающих акселерометр и гироскоп. Второй вариант применим к ИНС, включающих дополнительно 3-х осевой магнитометр (аббревиатура MARG — расшифровывается как “Magnetic, Angular Rate and Gravity”). Реализация ИНС с магнитометром подразумевает компенсацию магнитных искажений и компенсацию смещения гироскопа. В качестве инструмента используются кватернионы, которые позволяют использовать данные акселерометра и магнитометра для аналитических вычислений и оптимизации методом градиентного спуска в получении погрешности направления гироскопа в виде производного кватерниона. Преимущества включают в себя:
- дешевизна по вычислительным ресурсам — 277 простых арифметических операций каждое обновление фильтра (109 операций без магнитометра);
- эффективность при низких частотах дискретизации (например 10 Гц);
- Содержит 1 (без магнитометра) или 2 настраиваемых параметра, определяемых на наблюдаемых характеристиках системы.
Точность оценивалась эмпирически с использованием коммерчески доступных датчиков ориентации. Эталонные значения ориентации получены с помощью оптической системы измерения. Простой метод калибровки для использования оптического измерительного оборудования представлен в данной работе.
Точность также сопоставлена с патентованным фильтром на основе метода Калмана для датчиков ориентации. Результаты показывают, что данный фильтр достигает уровня точности, превышающий фильтр на основе метода Калмана:
< 0,6 градусов среднеквадратичное отклонение в неподвижном состоянии;
< 0,8 градусов среднеквадратичное отклонение в подвижном состоянии.
В следствие низкой вычислительной нагрузки и способности работать на низких частотах дискретизации открываются новые возможности применения ИНС для устройств реального времени с малыми вычислительными способностями и требованиями к высокой частоте выборок.
1. Введение
Точное определение ориентации в пространстве играет важную роль во многих областях, включая:
- Аэрокосмическую [1, 2, 3];
- Робототехнику [4, 5];
- Навигацию [6, 7];
- Анализ движений человека [8, 9]
- Взаимодействие движений человека и машины [10].
В то время как различные технологии позволяют измерять ориентацию, инерционные сенсорные системы имеют преимущество в виде полной автономности — измеряемый объект не ограничен в перемещениях, не ограничен какой-то конкретной средой или расположением. Блок инерциальных измерений (БИИ, или от англ. IMU — Inertial Measurement Unit) состоит из гироскопов и акселерометров позволяющих отслеживать вращательные и поступательные движения. Для того, чтобы делать 3D замеры, требуется чтобы оси датчиков были взаимно перпендикулярны. АГМ представляет собой гибрид БИИ, который включает в себя трехосный магнитометр. Система без магнитометра может определять ориентацию относительно направления силы тяжести, что достаточно для многих приложений [4, 2, 8, 1]. Инерциальные навигационные системы используют систему отчёта, известную как “курс, тангаж, крен” (англ. AHRS — Attitude and Heading Reference Systems), и в состоянии обеспечить полное измерение ориентации относительно силы тяжести и земного магнитного поля.
Гироскоп измеряет угловую скорость, которую при известных начальных условиях можно интегрировать с течением времени, чтобы получать ориентацию датчика [11, 12]. Точные гироскопы, например кольцевой лазер, слишком дороги и громоздки для большинства приложений. С другой стороны менее точные MEMS-датчики (Micro Electrical Mechanical System — микромеханические электронные системы) используются в большинстве приложений [13]. Интеграция ошибок измерения приведёт к накоплению ошибки в вычислении ориентации.Таким образом гироскопы, сами по себе, не могут обеспечить абсолютное измерение ориентации. Акселерометр и магнетометр измеряют гравитационные и магнитные поля нашей планеты, и соответственно могут определять абсолютное значение ориентации в пространстве.
Тем не менее и они вероятнее всего будут подвержены воздействию высоких уровней шума. Например ускорение из-за движения приведёт к сдвигу контролируемого направления силы тяжести. Задача фильтра ориентации состоит в вычислении единой оценки ориентации полученной путём измерений акселерометра, гироскопа и магнитометра.
Фильтр Калмана [14] стал признанной основой для построения большинства алгоритмов определения ориентации [4, 15, 16, 17] и коммерческих систем ориентации и инерциальных модулей:
- xsens [18],
- Microstrain [19],
- VectorNav [20],
- InterSense [21],
- PNI [22],
- Crossbow [23],
— все они основаны на его использовании. Широкое использование решений Калмана являются доказательством их точности и эффективности, однако они имеют ряд недостатков. Они могут быть сложны в реализации, что показано в имеющейся литературе [3, 4, 15, 16, 17, 24, 25, 26, 27, 28, 29, 30, 31, 32]. Линейная регрессия итерации, является основополагающим для процессов Калмана, требования к частоте дискретизации, значительно превышающие пропускную способность объекта. Например, частота дискретизации между 512 Гц и 30 кГц может быть использована в приложениях захвата движения. Состояние отношения, описывающего вращающеюся кинематику в трёх измерениях, как правило, требуют больше векторов состояния и реализации расширенного фильтра Калмана [4, 17, 24] для линеаризации задачи.
Эти проблемы требуют большой вычислительной нагрузки для реализации решений Калмана, но и обеспечения чётких мотивов для реализации альтернативных подходов. Многие предыдущие подходы к решению этих вопросов были основаны либо на нечёткой обработке [2, 5] или на фиксации фильтра [33] в пользу акселерометра для определения ориентации на малых угловых скоростях и интегрирование измерений гироскопа при обнаружении высоких угловых скоростей. Такой подход прост, но может быть эффективным только при ограниченных условиях эксплуатации. Бахман и другие [34] предложили альтернативный подход, при котором фильтр достигает оптимального синтеза данных измерений на всех угловых скоростях. Тем не менее, процесс требует аппроксимации методом наименьших квадратов, что также добавляет вычислительной нагрузки. Махони и другие [35] разработали комплиментарный фильтр, который, как показывает практика, является эффективным и действенным решением. Однако, точность годится только для ИНС без магнитометра.
Эта статья описывает новый фильтр ориентации, который применим как к ИНС без магнитометра, так и к ИНС с магнитометром. Фильтр занимается обработкой массивов данных поступающих с датчиков и снимает проблемы точности и настройки параметров фильтров, основанных на подходах Калмана. Фильтр использует кватернион для представления ориентации (например [34, 17, 24, 30, 32]), чтобы описать положение в пространстве в трёх измерениях и не содержит проблем, связанных с описанием положения углами Эйлера (складывание рамок). В статье представлен полный вывод и эмпирические оценки нового фильтра. Его точность сопоставлена с уже существующими промышленными фильтрами и проверены системой оптического измерения. Инновационные аспекты предлагаемого фильтра включают в себя:
- два регулируемых параметра (один для реализации без магнитометра) определяемых наблюдаемыми характеристиками системы;
- аналитические вычисления и оптимизация методом градиентного спуска, что повышает точность при малых частотах дискретизации;
- компенсация магнитных искажений и компенсация смещения нуля гироскопа в режиме реального времени.
2. Кватернионы
Этот раздел статьи не так интересен — в нём описывается, что такое кватернион и некоторые базовые операции. Всё это можно посмотреть в статье с картинками. Нам важно обратить внимание на используемую автором систему обозначений.
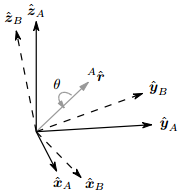
Рис. 1. Ориентация осей В достигается путём вращения осей А вокруг оси
 в системе отчёта А на угол θ.
в системе отчёта А на угол θ.Кватернион — это четырехмерное комплексное число, которое может быть использовано для представления ориентации остроконечного тела или координат в трехмерном пространстве. Описать ориентацию системы отчёта B по отношению к системе отчёта A можно с помощью поворота на угол θ вокруг оси
 в системе отчёта А. Это изображено на рисунке 1, где взаимно ортогональные орты
в системе отчёта А. Это изображено на рисунке 1, где взаимно ортогональные орты 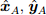 ,
, 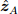 и
и  определены главной осью систем координат А и В соответственно. Кватернион, описывающий эту ориентацию
определены главной осью систем координат А и В соответственно. Кватернион, описывающий эту ориентацию 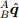 определяется уравнением (1), где Rx, Ry и Rz являются компонентами вектора
определяется уравнением (1), где Rx, Ry и Rz являются компонентами вектора  в соответствующих осях X, Y и Z системы отчёта А. Для именования переменных, систем отчёта и векторов принята система обозначений надстрочными и подстрочными индексами по Крэйгу [37].
в соответствующих осях X, Y и Z системы отчёта А. Для именования переменных, систем отчёта и векторов принята система обозначений надстрочными и подстрочными индексами по Крэйгу [37]. Впереди стоящий нижний индекс обозначает целевую систему отчёта, а впереди стоящий верхний индекс обозначает систему отчёта относительно которой задана переменная. Далее в тексте индекс S обозначает систему отчёта датчика, а индекс E систему отчёта Земли. Например,
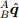 описывает ориентацию осей B по отношению к осям A, а
описывает ориентацию осей B по отношению к осям A, а  представляет собой вектор в системе отчёта А. Кватернионная арифметика часто требует, чтобы кватернион был нормализован к единице. Поэтому обычно все кватернионы описывающие ориентацию имеют длину равную единице.
представляет собой вектор в системе отчёта А. Кватернионная арифметика часто требует, чтобы кватернион был нормализован к единице. Поэтому обычно все кватернионы описывающие ориентацию имеют длину равную единице.
Обратите внимание — в данной статье компонента W кватерниона идёт первой (нередко её помещают в конце).
Противонаправленные кватернионы обозначаются * (звёздочкой) и используются для изменения системы отчёта. Например
 противонаправлен по отношению к
противонаправлен по отношению к 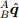 * и описывает ориентацию системы отчёта A по отношению к B. Противонаправленный вектор к
* и описывает ориентацию системы отчёта A по отношению к B. Противонаправленный вектор к 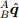 определяется уравнением (2).
определяется уравнением (2).
Кватернион, получаемый в результате операции
 может быть использован для определения составных ориентаций (серии поворотов). Например, для двух ориентаций
может быть использован для определения составных ориентаций (серии поворотов). Например, для двух ориентаций 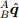 и
и 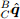 может быть найдена
может быть найдена  по формуле (3).
по формуле (3).
Результат умножения для двух кватернионов a и b может быть найден с помощью правила Гамильтона и определяется формулой (4). При перемене мест множителей результат разный (умножение кватернионов ассоциативно, но не коммутативно).
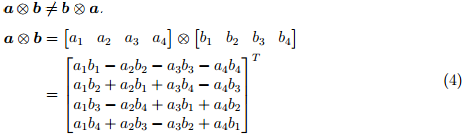
Трехмерный вектор может быть повернут на кватернион с помощью отношения, описанного в уравнении (5) [36].
 и
и 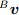 это векторы в системе координат А и B соответственно, где каждый вектор содержит 0 в качестве компоненты W, чтобы сделать их 4 компонентными векторами (кватернионами).
это векторы в системе координат А и B соответственно, где каждый вектор содержит 0 в качестве компоненты W, чтобы сделать их 4 компонентными векторами (кватернионами).

Ориентация описываемая кватернионом
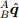 может быть описана в виде матрицы вращения
может быть описана в виде матрицы вращения 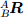 определяемой по формуле (6) [36].
определяемой по формуле (6) [36].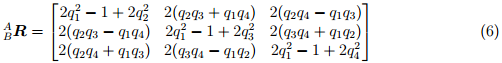
Углы Эйлера ψ, θ и φ в так называемой аэрокосмической последовательности [36] описывают ориентацию осей достигаемую за счет последовательных вращений относительно системы отчёта А, с помощью угла ψ вокруг оси Z, θ вокруг оси Y, и φ вокруг оси X. Такие углы Эйлера можно получить из кватерниона
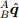 с помощью уравнений (7), (8) и (9).
с помощью уравнений (7), (8) и (9).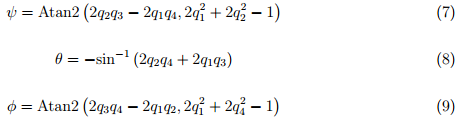
3. Фильтр
3.1. Ориентация из угловой скорости
Трёхосевой гироскоп измеряет угловые скорости ωx, ωy и ωz относительно осей X, Y, Z соответственно, в системе отчёта датчика. Если значения этих скоростей (рад/сек) преобразовать в кватернион
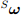 определённым уравнением (10), то производный кватернион, описывающий скорость в системе отчёта Земли по отношению к системе отчёта датчика
определённым уравнением (10), то производный кватернион, описывающий скорость в системе отчёта Земли по отношению к системе отчёта датчика  может быть вычислен [38] уравнением (11):
может быть вычислен [38] уравнением (11):
Откуда взялась 1/2?
Долго не мог понять — откуда взялась 1/2-я? Это связано с определением кватерниона:… кватернион q определяется как q = w + xi + yj + zk = w + (x,y,z) = cos (a/2) + u*sin (a/2),
где u — единичный вектор.
В статье о угловой скорости имеется формула, которая выражается из (11):
Если для описания поворота используется кватернион, выражаемый через угол a и орт оси поворота v как q = (cos (a/2), v*sin(a/2)), то угловая скорость находится из выражения:
 ,
,
где обозначения в формуле совпадают с обозначениями в статье — кватернион с точкой описывает угловую скорость в системе отчёта Земли, а кватернион с чёрточкой описывает поворот, необходимый для совмещения системы отчёта датчика с системой отчёта Земли.
где u — единичный вектор.
В статье о угловой скорости имеется формула, которая выражается из (11):
Если для описания поворота используется кватернион, выражаемый через угол a и орт оси поворота v как q = (cos (a/2), v*sin(a/2)), то угловая скорость находится из выражения:
 ,
, где обозначения в формуле совпадают с обозначениями в статье — кватернион с точкой описывает угловую скорость в системе отчёта Земли, а кватернион с чёрточкой описывает поворот, необходимый для совмещения системы отчёта датчика с системой отчёта Земли.
Ориентация в глобальной системе отчёта по отношению к локальной системе отчёта датчика в момент t это
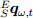 , может быть вычислена путем численного интегрирования кватернионов производных
, может быть вычислена путем численного интегрирования кватернионов производных  , так как описано в уравнениях (12) и (13), при условии, что начальная ориентация в пространстве известна.
, так как описано в уравнениях (12) и (13), при условии, что начальная ориентация в пространстве известна.
где
 — угловая скорость, измеренная датчиком в момент времени t;
— угловая скорость, измеренная датчиком в момент времени t;∆t — задержка между измерениями (период дискретизации);
 — предыдущий результат оценки ориентации.
— предыдущий результат оценки ориентации.Индекс ω указывает, что кватернион вычисляется из угловых скоростей.
3.2. Ориентация из векторных наблюдений
Трёхосевой акселерометр измеряет величину и направление поля тяготения в локальной системе координат вместе с линейными ускорениями вследствие движения датчика. Точно так же трёхосевой магнитометр измеряет величину и направление магнитного поля земли в локальной системе отчёта вместе с локальными магнитными искажениями. В контексте фильтра ориентации, он в начальный момент времени будет предполагать, что акселерометр будет измерять только гравитацию, магнитометр измеряет только магнитное поле Земли (прибор должен быть неподвижен какое-то время).
Если направление поля Земли известно в её системе координат, то измерение направления в системе координат датчика позволит рассчитать положение системы координат датчика относительно системы координат Земли. Однако для любого такого измерения не будет единственного решения, а будет бесконечное число решений, представленные всеми теми ориентациями, достигаемыми за счёт вращения ориентации вокруг вращения, параллельного направлению поля (магнитного или гравитации). В некоторых случаях можно решение представить в виде углов Эйлера, где будет два известных угла и один неизвестный. Неизвестный угол будет вращаться вокруг оси параллельной направлению поля. Для представления решения кватернионом требуется комплексное решение. Этого можно достичь путём задачи оптимизации, где ориентация датчика
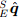 это то, что выравнивает определённое заранее направление поля в земной системе координат
это то, что выравнивает определённое заранее направление поля в земной системе координат 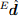 , с измеренным направлением в системе координат датчика
, с измеренным направлением в системе координат датчика 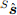 с помощью операции вращения, определяемой уравнением (5). Поэтому
с помощью операции вращения, определяемой уравнением (5). Поэтому 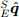 может быть найдено как решение уравнения (14), где уравнение (15) определяет целевую функцию. Компоненты каждого вектора определяются в уравнениях (16), (17) и (18).
может быть найдено как решение уравнения (14), где уравнение (15) определяет целевую функцию. Компоненты каждого вектора определяются в уравнениях (16), (17) и (18).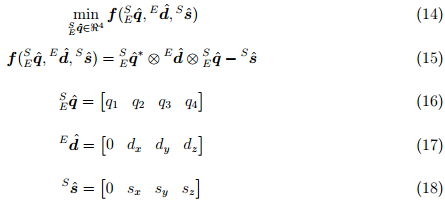
Существует множество алгоритмов оптимизации, но метод градиентного спуска является одним из простейших в реализации и вычислениях. Уравнение (19) описывает данный метод для n итераций в результате оценки ориентации
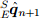 на основе «начального приближения» ориентации
на основе «начального приближения» ориентации 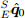 и размера шага µ. Уравнение (20) вычисляет градиент поверхности решений, определяемой целевой функцией и её Якобиан, упрощённый к трёхкомпонентным векторам, определённых в уравнениях (21) и (22) соответственно.
и размера шага µ. Уравнение (20) вычисляет градиент поверхности решений, определяемой целевой функцией и её Якобиан, упрощённый к трёхкомпонентным векторам, определённых в уравнениях (21) и (22) соответственно.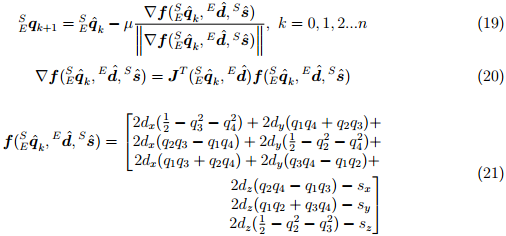
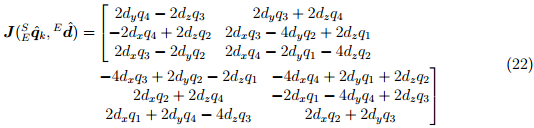
Уравнения (19) — (22) описывают общий вид алгоритма.применимого к полю, изначально ориентированного в любом направлении. Однако, если направление поля можно считать только в одной или двух осях глобальной системы координат, уравнение упрощается. Соответствующее соглашение будет предполагать, что направление силы тяжести направлено вертикально, вдоль оси Z, как показано в уравнении (23). Подставляя кватернион
 и нормализованные измерения акселерометра
и нормализованные измерения акселерометра  ,
,  и
и 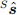 соответственно в уравнения (21) и (22) получим уравнение (25) и (26).
соответственно в уравнения (21) и (22) получим уравнение (25) и (26).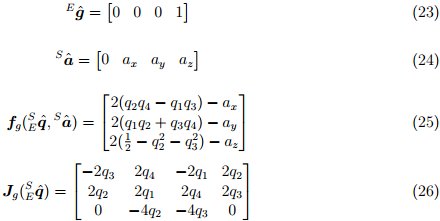
Направление магнитного поля земли можно считать также располагается в одной плоскости и измеряется в горизонтальной и вертикальной осях. Вертикальная составляющая зависит от точки на Земном шаре, в котором происходит измерение. Для Англии это значение находится в пределах между 65 и 70 градусами по отношению к горизонту [39]. Это может быть представлено уравнением (27). Подставляя
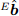 и нормализованные значения измерений
и нормализованные значения измерений  ,
,  и
и  соответственно в уравнения (21) и (22) получим уравнения (29) и (30).
соответственно в уравнения (21) и (22) получим уравнения (29) и (30).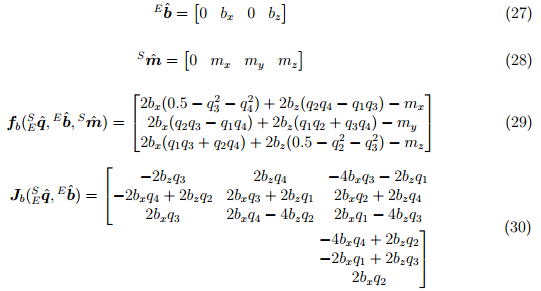
Как уже обсуждалось, измерение силы тяжести или магнитного поля Земли сами по себе не обеспечивают уникальную ориентацию датчика. Чтобы сделать это, измерения и отношения направления обоих полей должны быть объединены, как описано в уравнениях (31) и (32). В то время как поверхность решений, созданная целевыми функциями в уравнениях (25) и (29) имеют, как минимум, определенный в соответствии с поверхностью решений определённом с помощью уравнения (31), так и минимум определённый по одной точке, при условии, что
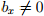 .
.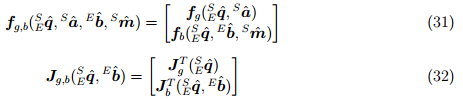
Традиционный подход к оптимизации потребует нескольких итераций уравнения (19), чтобы вычислить результат для каждой новой ориентации и соответствующих измерений датчиков. Эффективные алгоритмы требуют также размер шага μ для корректировки результата на каждой итерации до оптимального значения, обычно получаемый на основе второй производной целевой функции, Гессе. Тем не менее, эти требования существенно повышают вычислительную нагрузку алгоритма и не являются необходимыми в нашем деле. Для нас приемлемо вычисление одной итерации на отсчет времени при условии, что скорость сходимости регулируемая µt равна или больше, чем физическая скорость изменения ориентации. Уравнение (33) вычисляет приблизительное направление
 вычисляемое в момент времени t на основе предыдущей оценки ориентации
вычисляемое в момент времени t на основе предыдущей оценки ориентации  и целевой функцией градиента ∇f определяемой путём измерений датчиков
и целевой функцией градиента ∇f определяемой путём измерений датчиков 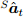 и
и 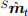 в момент времени t. Форма ∇f выбирается в соответствии с датчиками в использовании, как показано в уравнении (34). Индекс ∇ означает, что кватернион вычисляется с использованием метода градиентного спуска.
в момент времени t. Форма ∇f выбирается в соответствии с датчиками в использовании, как показано в уравнении (34). Индекс ∇ означает, что кватернион вычисляется с использованием метода градиентного спуска.
Оптимальное значение µt может быть определено как то, которое обеспечивает скорость сходимости
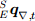 и ограничивается физической скоростью ориентации, так как это позволяет избежать превышения из-за излишне большого размера шага. Поэтому µt может быть вычислено с помощью уравнения (35), где ∆t — это время между замерами,
и ограничивается физической скоростью ориентации, так как это позволяет избежать превышения из-за излишне большого размера шага. Поэтому µt может быть вычислено с помощью уравнения (35), где ∆t — это время между замерами,  — это физическая скорость изменения ориентации, измеренная гироскопом, α — это увеличение µ для учёта шума при измерениях акселерометром и магнитометром.
— это физическая скорость изменения ориентации, измеренная гироскопом, α — это увеличение µ для учёта шума при измерениях акселерометром и магнитометром.
3.3. Алгоритм объединяющего фильтра
Мы видим, что ориентация датчика по отношению к Земле
 получается путём объединения расчётов ориентации
получается путём объединения расчётов ориентации 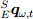 и
и  , рассчитываемые с помощью уравнений (13) и (33) соответственно. Объединение
, рассчитываемые с помощью уравнений (13) и (33) соответственно. Объединение 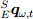 и
и  описывается уравнением (36), где γt and (1 − γt) — это веса, применяемые к каждому расчёту ориентации.
описывается уравнением (36), где γt and (1 − γt) — это веса, применяемые к каждому расчёту ориентации.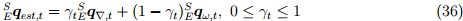
Оптимальное значение γt может быть определено как то, при котором взвешенная расходимость
 равна взвешенной сходимости
равна взвешенной сходимости  . Это представлено уравнением (37), где
. Это представлено уравнением (37), где  — это скорость сходимости
— это скорость сходимости  , а β — это скорость расхождения
, а β — это скорость расхождения  , выраженная в виде величины кватерниона, производного от соответствующей погрешности измерений гироскопа. Уравнение (37) может быть изменено, чтобы определить γt в уравнение (38).
, выраженная в виде величины кватерниона, производного от соответствующей погрешности измерений гироскопа. Уравнение (37) может быть изменено, чтобы определить γt в уравнение (38).
Уравнения (36) и (38) обеспечивают оптимальное сочетание
 и
и 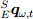 при условии, что скорость сходимости
при условии, что скорость сходимости  регулируется α, которая больше либо равна чем физическая скорость изменения ориентации. Поэтому α не имеет верхней границы. Если считать α очень большой, то µt определяется выражением (35), а также становится и очень большим значения в упрощённом уравнении фильтра ориентации. Большие значения µt использованные в уравнении (33) означают, что
регулируется α, которая больше либо равна чем физическая скорость изменения ориентации. Поэтому α не имеет верхней границы. Если считать α очень большой, то µt определяется выражением (35), а также становится и очень большим значения в упрощённом уравнении фильтра ориентации. Большие значения µt использованные в уравнении (33) означают, что  становится пренебрежительно мало и уравнение можно переписать в виде выражения (39).
становится пренебрежительно мало и уравнение можно переписать в виде выражения (39).
Уравнение (38), вычисляющее γt, может быть дополнительно упрощено путём принятия незначительности величин β в знаменателе и выражение тогда можно переписать в виде уравнения (40). Из уравнения (40) вполне возможно, что γt ≈ 0.

Подставляя уравнения (13), (39) и (40) в уравнение (36) получаем непосредственно уравнение (41). Обратите внимание, что γt в уравнении (41) заменяется и как выражение (39) и как 0.
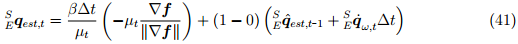
Уравнение (41) можно упростить до уравнения (42), где
 — это расчётная скорость изменения ориентации, определяемая выражением (43);
— это расчётная скорость изменения ориентации, определяемая выражением (43);  — это направление ошибки
— это направление ошибки  , определяемое выражением (44).
, определяемое выражением (44).
Из уравнений (42), (43) и (44) видим, что фильтр вычисляет ориентацию
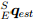 путем численного интегрирования расчетной скорости ориентации
путем численного интегрирования расчетной скорости ориентации  . Фильтр вычисляет
. Фильтр вычисляет  как скорость изменения ориентации, измеренной гироскопом,
как скорость изменения ориентации, измеренной гироскопом, 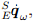 то же, но ещё с ошибкой измерения гироскопа, β — это компенсация в направлении предполагаемой ошибки;
то же, но ещё с ошибкой измерения гироскопа, β — это компенсация в направлении предполагаемой ошибки; 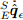 вычисляется на основании измерений акселерометра и магнитометра. Рис. 2 показывает блок-схему полной реализации фильтра ориентации для ИНС.
вычисляется на основании измерений акселерометра и магнитометра. Рис. 2 показывает блок-схему полной реализации фильтра ориентации для ИНС.
Рис. 2. Блок-схема представляющая полную реализацию фильтра ориентации для ИНС
3.4. Компенсация магнитных искажений
Измерения магнитного поля Земли будут искажены наличием ферромагнитных источников вблизи датчика. Исследования по влиянию магнитных искажений на эффективность датчика ориентации показали, что существенную погрешность вносят: электроприборы, металлическая мебель и металлоконструкции использованные при строительстве зданий [40, 41]. Источники помех в системе отчёта датчика, могут быть компенсированы путём его калибровки [42, 43, 44, 45]. Источники помех в системе отчёта Земли, вызываемые например месторождениями железа, вызывают ошибки в контролируемом направлении магнитного поля Земли. Ошибки склонения, которые в горизонтальной плоскости по отношению к земной поверхности, не могут быть скомпенсированы без дополнительной информации о курсе. Ошибки наклона в вертикальной плоскости, могут быть скомпенсированы по акселерометру, который обеспечивает дополнительное измерение относительно датчика.
Контролируемое направление магнитного поля Земли в земных координатах в момент времени t,
 , может быть вычислено как нормированное значение измерений магнитометра
, может быть вычислено как нормированное значение измерений магнитометра 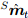 , вращаемое ориентацией, полученной объединяющим фильтром
, вращаемое ориентацией, полученной объединяющим фильтром 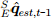 , как описано в уравнении (45). Эффект ошибочного наклона магнитного поля в контролируемом направлении Земли
, как описано в уравнении (45). Эффект ошибочного наклона магнитного поля в контролируемом направлении Земли  может быть исправлен, если относительное направление магнитного поля земли
может быть исправлен, если относительное направление магнитного поля земли  всё время имеет тот же самый наклон. Это достигается путём вычисления нормалей
всё время имеет тот же самый наклон. Это достигается путём вычисления нормалей  и
и  только на оси X и Y в системе отчёта Земли, что описано в уравнении (46).
только на оси X и Y в системе отчёта Земли, что описано в уравнении (46).
Компенсация магнитных искажений в этом случае гарантирует, что магнитные возмущения влияют только на курс. Подход также устраняет необходимость задавать заранее направление магнитного поля Земли, что является потенциальным недостатком других подходов в фильтрах ориентации [17, 24].
3.5. Компенсация дрейфа нуля гироскопа
Дрейф нуля гироскопа будет происходить от изменения температур, от движения и просто со временем. Любая практическая реализация ИНС должна учитывать это. Преимуществом Калмано-подобных решений является то, что они способны оценить смещение гироскопа в качестве дополнительного состояния в рамках модели системы [26, 30, 15, 24]. Тем не менее Махони и др. [35] показали, что дрейф нуля гироскопа также может быть скомпенсирован простыми фильтрами ориентации, представляя его как часть ошибки от скорости изменения ориентации. Аналогичный подход будет использоваться здесь.
Нормированное направление расчетной ошибки в скорости изменения ориентации
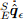 может быть выражена как угловая погрешность по каждой оси гироскопа с использованием уравнения (47) и получается как обратное отношение из уравнения (11). Смещение гироскопа
может быть выражена как угловая погрешность по каждой оси гироскопа с использованием уравнения (47) и получается как обратное отношение из уравнения (11). Смещение гироскопа  представлено как DC-составляющая
представлено как DC-составляющая 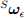 и поэтому может быть удалена, так как часть
и поэтому может быть удалена, так как часть 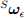 средневзвешенное соответствующим усилением ζ. Это даёт компенсацию измерений гироскопа
средневзвешенное соответствующим усилением ζ. Это даёт компенсацию измерений гироскопа 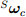 как показано в уравнениях (48) и (49). Предполагается, что первый элемент
как показано в уравнениях (48) и (49). Предполагается, что первый элемент 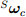 всегда равен 0.
всегда равен 0.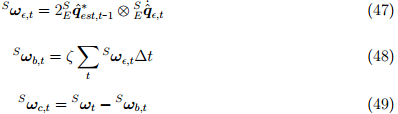
Скомпенсированные измерения гироскопа
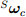 могут быть использованы вместо исходных измерений гироскопа
могут быть использованы вместо исходных измерений гироскопа 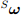 в уравнении (11). Величина угловой погрешности в каждой оси
в уравнении (11). Величина угловой погрешности в каждой оси 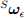 равна кватерниону единичной длины. Поэтому встроенный коэффициент усиления ζ непосредственно определяет скорость сходимости предполагаемого смещения гироскопа
равна кватерниону единичной длины. Поэтому встроенный коэффициент усиления ζ непосредственно определяет скорость сходимости предполагаемого смещения гироскопа  выраженного в виде производного кватерниона. Так как этот процесс требует полной оценки ориентации фильтра
выраженного в виде производного кватерниона. Так как этот процесс требует полной оценки ориентации фильтра 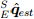 это применимо только к реализации фильтра с магнитометром. Рис. 3 показывает блок-схему представления полной реализации фильтра для ИНС с магнитометром, включающий компенсацию магнитных искажений и дрейфа гироскопа.
это применимо только к реализации фильтра с магнитометром. Рис. 3 показывает блок-схему представления полной реализации фильтра для ИНС с магнитометром, включающий компенсацию магнитных искажений и дрейфа гироскопа.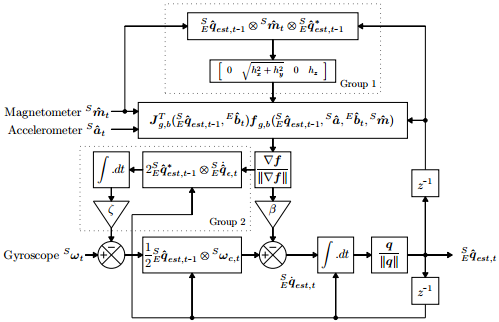
Рис. 3. Блок-схема представляющая полный фильтр ИНС с магнитометром включающий компенсацию магнитного искажения (группа 1) и компенсацию дрейфа гироскопа (группа 2).
3.6. Коэффициенты усиления фильтра
Коэффициент усиления фильтра β представляет все ошибки измерений нуля гироскопа, выраженные как величина производного кватерниона. Источники ошибки: шум датчика, сглаживающий фильтр, ошибки квантования, ошибки калибровки, ошибки установки и выравнивания датчика, неортогональность осей датчика и частотные характеристики. Коэффициент усиления фильтра ζ представляет собой скорость сходимости для удаления ошибок измерения гироскопа, не связанных с нулём и также выражен как величина производного кватерниона. Эти ошибки представляют собой смещение гироскопа. Определять β и ζ удобно с помощью угловых величин
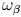 и
и 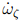 соответственно, где
соответственно, где 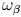 представляет оценку средней погрешности измерения нуля по каждой оси, а
представляет оценку средней погрешности измерения нуля по каждой оси, а 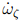 представляет расчётную скорость дрейфа гироскопа в каждой оси. Используя соотношение описанное уравнением (11), β может быть определена уравнением (50), где
представляет расчётную скорость дрейфа гироскопа в каждой оси. Используя соотношение описанное уравнением (11), β может быть определена уравнением (50), где 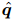 представляет всякий единичный кватернион. Аналогичным образом, ζ может быть описано с помощью уравнения (51).
представляет всякий единичный кватернион. Аналогичным образом, ζ может быть описано с помощью уравнения (51).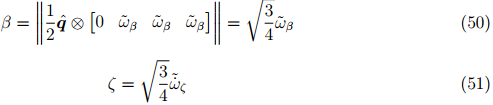
4. Испытания
4.1 Оборудование
Фильтр был протестирован с использованием блока датчиков ориентации xsens MTX [18], содержащий 16-битные трехосевые: гироскоп, акселерометр и магнитометр. Устройство и соответствующее программное обеспечение используют режим операций, где сырые данные с датчиков поступают с частотой 512 Гц, а затем обрабатываются, чтобы обеспечить калиброванные измерения датчика. Калиброванные измерения датчика могут быть обработаны с помощью предлагаемого фильтра, чтобы обеспечить расчетную ориентацию датчика. Программное обеспечение также включает в себя вычисление дополнительной оценки ориентации Калмано-подобным фильтром. Оба фильтра — Калмано-подобный и предложенный, могут работать с использованием одних и тех же выходных данных датчиков. Точность каждого алгоритма оценивается по отношению к друг другу как точность независимых датчиков.
Система Vicon, состоящая из 8 MX3 + камера, подключенные к серверу MXultranet [46] и Nexus [47] программное обеспечение было использовано, чтобы обеспечить опорные измерения фактической ориентировки датчика ориентации. Система массива ИК (инфракрасный) чувствительных камер с включенными прожекторами IR. Камеры фиксируют на калиброванных положениях и ориентациях так, чтобы объект измерения был в поле зрения нескольких камер. Декартовы позиции ИК отражающих оптических маркеров, закрепленных на объект измерения могут быть вычислены в системе координат массива камер. Камеры были установлены на высоте примерно 2,5 м и равномерно распределены по всему периметру площадки 4 м на 4 м. Каждая камера была сориентирована на центр комнаты, приблизительно от 30◦ до 60◦ к горизонтали. Эксперименты проводились с объектом измерения в центре комнаты на высоте примерно 1 м. Для измерения ориентации датчика, он был прикреплен к измерительной платформе оптической ориентации, специально предназначенной для этого эксперимента. Система использовалась, чтобы регистрировать позиции оптических маркеров со скоростью 120 Гц.
4.2 Определение ориентации из оптических измерений
Платформа измерения ориентации состоит из 3,5 м, взаимно ортогональных стержней, жестко соединенных в центре.На каждом конце стержня закреплены оптические маркеры и в их пересечении закреплена платформа с датчиком ориентации. Платформа была изготовлена из алюминия, стержни из углеродного волокна и всё собрано с использованием клеев для того, чтобы у конструкции не было магнитных свойств, которые могут помешать магнетометру. Дополнительные оптические маркеры были помещены в произвольных положениях вдоль длины стержней нарушая осевую симметрию для того, чтобы помочь идентифицировать каждый стержень в данном измерении. На рис. 4 представлена фотография платформы измерения ориентации, где
 ,
, 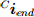 ,
,  ,
,  ,
,  и
и  — это измеренное положение каждого маркера рамки в пределах видимости камеры. Эти позиции могут быть использованы для определения 3-х взаимно ортогональных векторов
— это измеренное положение каждого маркера рамки в пределах видимости камеры. Эти позиции могут быть использованы для определения 3-х взаимно ортогональных векторов  ,
,  и
и  в системе координат камеры, получая направления осей платформы X, Y, Z так. как это показано в уравнении (52), (53) и (54). Эти векторы определяют матрицу вращения, описывающую ориентацию измерительной платформы в системе координат камеры, как показано в уравнении (55).
в системе координат камеры, получая направления осей платформы X, Y, Z так. как это показано в уравнении (52), (53) и (54). Эти векторы определяют матрицу вращения, описывающую ориентацию измерительной платформы в системе координат камеры, как показано в уравнении (55).
Рис. 4. Фотография платформы измерения ориентации
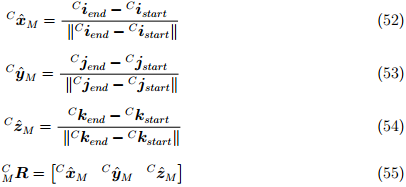
Из-за ошибок измерений и допусков в конструкции рамки с маркерами, матрица вращения, определяемая уравнением (55), не может считаться ортогональной и поэтому не представляет собой чистое вращение. Бар-Ицхак представляет нам метод (48), где по оптимальному «лучшему соответствию» может быть извлечён кватернион из не точной и не ортогональной матрицы поворота. Метод требует построения симметричной матрицы 4х4, К, определяемую уравнением (56), где
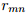 соответствует m-ной строке n-ого столбца
соответствует m-ной строке n-ого столбца  . Оптимальный кватернион
. Оптимальный кватернион  находится как нормализованный собственный вектор, соответствующий максимальному собственному значению матрицы К. Уравнение (57) определяет оптимальную альтернативу. Уравнение (57) определяет оптимальный альтернативный кватернион, как условно предполагается методом, где V1, V2, V3 и V4 определяют элементы нормализованного собственного вектора.
находится как нормализованный собственный вектор, соответствующий максимальному собственному значению матрицы К. Уравнение (57) определяет оптимальную альтернативу. Уравнение (57) определяет оптимальный альтернативный кватернион, как условно предполагается методом, где V1, V2, V3 и V4 определяют элементы нормализованного собственного вектора.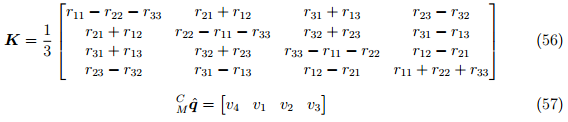
4.3 Калибровка совмещения систем отчёта
Для того, чтобы сравнить оптические измерения ориентации платформы в кадре камеры,
 , и предполагаемую фильтром ориентацию относительно Земли,
, и предполагаемую фильтром ориентацию относительно Земли,  , требуется знать выравнивание системы отчёта Земли относительно системы отчёта камеры,
, требуется знать выравнивание системы отчёта Земли относительно системы отчёта камеры,  , и выравнивание измерительной платформы, относительно системы отчёта датчика
, и выравнивание измерительной платформы, относительно системы отчёта датчика 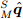 . После того, как эти величины найдены, оптическое измерение ориентации датчика в системе отчёта Земли,
. После того, как эти величины найдены, оптическое измерение ориентации датчика в системе отчёта Земли,  , определяется по формуле (58). Хотя использование оптического оборудования описано в приложениях к документам [26, 24, 41], есть предложение немного обсудить калибровку этих двух величин.
, определяется по формуле (58). Хотя использование оптического оборудования описано в приложениях к документам [26, 24, 41], есть предложение немного обсудить калибровку этих двух величин.
Оси X и Z системы отчёта Земли определяются её магнитным полем и гравитацией. Измерение этих полей в системе отчёта камеры могут быть использованы для выравнивания
 . Направление силы тяжести определяют с помощью нити с грузиком (маятника), длиной 1 метр, прикреплённой к платформе.Оптический маркер помещается на грузике и достигается окончание раскачивания, т. е. грузик приводится в неподвижное состояние.
. Направление силы тяжести определяют с помощью нити с грузиком (маятника), длиной 1 метр, прикреплённой к платформе.Оптический маркер помещается на грузике и достигается окончание раскачивания, т. е. грузик приводится в неподвижное состояние.Дополнительный оптический маркер требуются при произвольном фиксированном месте относительно статического маятника (грузика), чтобы нарушить осевую симметрию «созвездия» оптических маркеров. Рис. 5 показывает прокомментированную фотографию маятника, где
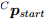 и
и  определяют положение маркеров в системе отчёта камеры. Среднее положение каждого маркера в течение определенного периода времени, определяет направление маятника в системе отчёта камеры,
определяют положение маркеров в системе отчёта камеры. Среднее положение каждого маркера в течение определенного периода времени, определяет направление маятника в системе отчёта камеры,  . Это непосредственно определяет ось Z системы отчёта Земли в системе отчёта камеры,
. Это непосредственно определяет ось Z системы отчёта Земли в системе отчёта камеры,  , как показано в уравнении (59).
, как показано в уравнении (59).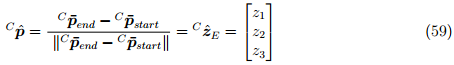

Рис. 5: Фотография маятника и оптических маркеров, используемых для измерения направления силы тяжести в системе отчёта камеры
Направление магнитного поля Земли было измерено с помощью магнитного компаса, изготовленного из метрового стержня из углеродного волокна с неодимовыми магнитами на концах, прикрепленных к каждому концу. Направление северного и южного полюса магнитов совпадает. Компас подвешен на хлопчатобумажной нити и приведен в состояние покоя. Оптические маркеры размещены на концах стержня, а также несимметрично в других местах вдоль стержня, чтобы нарушить осевую симметрию «созвездия» (вероятно чтобы идентифицировать каждый конец). На рис. 6 показана прокомментированная фотография компаса, где
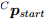 и
и  определяю положние оптических маркеров в системе отчёта камеры. Среднее положение каждого маркера в течении некоторого периода времени определяет положение компаса в системе отчёта камеры,
определяю положние оптических маркеров в системе отчёта камеры. Среднее положение каждого маркера в течении некоторого периода времени определяет положение компаса в системе отчёта камеры, 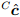 , как показано в выражении (60).
, как показано в выражении (60).
Рисунок 6: Фотография магнитного компаса и оптических маркеров, используемых для измерения направления магнитного поля Земли в системе отчёта камеры

Из-за ошибок измерения и дисбаланса подвешенного магнитного компаса,
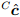 нельзя считать ортогональным по направлению к силе тяжести, определённого как
нельзя считать ортогональным по направлению к силе тяжести, определённого как  и поэтому
и поэтому 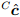 не может быть использовано для прямого определения оси X Земли. Неортогональность
не может быть использовано для прямого определения оси X Земли. Неортогональность 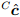 может быть вычислена как проекция
может быть вычислена как проекция 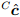 на ось
на ось  . Эта составляющая может быть удалена из
. Эта составляющая может быть удалена из 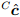 для определения направления оси X Земли в системе отчёта камеры
для определения направления оси X Земли в системе отчёта камеры 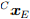 , как показано в выражении (61). После нормализации мы получаем ось Х Земли,
, как показано в выражении (61). После нормализации мы получаем ось Х Земли, 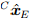 , как показано в выражении (62).
, как показано в выражении (62).
Ось Y системы отчёта Земли в системе отчёта камеры
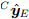 может быть вычислено как перпендикуляр к
может быть вычислено как перпендикуляр к 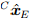 и
и  , как определено в уравнении (63) и где знаки выбираются так, чтобы направление осей соответствовало соглашению (имеется ввиду правая и левая система координат). Выравнивание земной системы отчёта может быть определено как матрица поворота
, как определено в уравнении (63) и где знаки выбираются так, чтобы направление осей соответствовало соглашению (имеется ввиду правая и левая система координат). Выравнивание земной системы отчёта может быть определено как матрица поворота 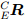 , построенная из
, построенная из 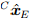 ,
, 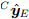 и
и  . Кватернионное представление
. Кватернионное представление  может быть получено по методу Бара-Ицхака [48].
может быть получено по методу Бара-Ицхака [48].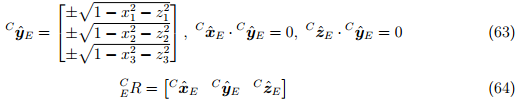
Для того, чтобы найти выравнивание
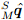 , предполагается, что статическая погрешность фильтра основанного на методе Калмана в среднем равна нулю. Средняя величина на выходе
, предполагается, что статическая погрешность фильтра основанного на методе Калмана в среднем равна нулю. Средняя величина на выходе  была вычислена при измерении платформы, находящейся в неподвижном состоянии в течении примерно 10 секунд. Это было использовано с выравниванием
была вычислена при измерении платформы, находящейся в неподвижном состоянии в течении примерно 10 секунд. Это было использовано с выравниванием  и оптическим измерением
и оптическим измерением  для определения выравнивания платформы в системе отчёта датчика
для определения выравнивания платформы в системе отчёта датчика 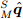 , как определено в выражении (65).
, как определено в выражении (65).
4.4. Процедура проведения экпериментов
Оптические данные измерения и сырые данные датчиков ориентации регистрировались одновременно. Затем сырые данные датчиков ориентации были обработаны соответствующей программой, чтобы откалибровать данные датчика и выход фильтра на основе Калмана. Эти данные затем синхронизируются с данными оптических измерений, при этом данные оптических измерений интерполируются из-за более высокой частоты замеров датчиков ориентации. Затем калиброванные данные датчиков обрабатываются с помощью обоих вариантов предлагаемого метода: с магнитометром и без. Оптические данные извлекаются методами описанными в 4.2 и 4.3.
Коэффициент усиления β предлагаемого фильтра был установлен в 0,033 для реализации без магнитометра и 0,041 для реализации с магнитометром. Обобщения из раздела 5.3 показывают, что найденные коэффициенты обеспечивают максимальную точность. Тем не менее, в течении первых 10 секунд использовался коэффициент 2,5, чтобы обеспечить сходимость алгоритма при начальных условиях.
Коэффициент усиления ζ, применимый только к варианту с гироскопом, был установлен в 0, так как калибровка датчиков ориентации не предполагает дрейф смещения гироскопа.
Данные были получены для последовательности поворотов произведённых вручную. Измерительная платформа приводится в состояние покоя на 20-30 секунд, чтобы дать время алгоритму стабилизироваться. Затем платформу поворачивают на 90◦ вокруг своей оси Х, а затем на 180◦ в противоположном направлении, а затем делается поворот на 90◦ для приведения платформы в исходное положение. Платформа между каждым вращением удерживается в неподвижном состоянии от 3 до 5 секунд. Эта последовательность затем повторяется для осей Y и Z. Пик угловой скорости измеряемый в течении каждого поворота составлял от 110◦/с до 190◦/с. Эксперимент повторялся 8 раз, чтобы получить представление о точности системы.
5. Результаты
Среди общепринятых методов количественной оценки характеристик фильтра ориентации [24, 26, 18, 19, 20, 21] мы видим среднеквадратичные ошибки в подвижном (динамические) и неподвижном (статические) состоянии в отрыве от углов Эйлера, описывающих курс, крен, тангаж. Тангаж φ, крен θ и курс ψ соответствуют вращению вокруг осей X, Y, Z соответственно в системе отчёта датчика. Вышеупомянутые углы отвязаны от углов Эйлера и могут быть более просто интерпретироваться и визуализироваться. Недостатком углов Эйлера является то, что в них не описывается связь между параметрами, а также они подвержены крупным неустойчивым ошибкам, когда значения некоторых углов достигают полюсов.
Углы Эйлера были вычислены непосредственно из получаемого кватерниона с использованием уравнений (7), (8) и (9).
В общей сложности были вычислены 4 набора параметров Эйлера, они соответствуют калиброванным оптическим измерениям ориентации, оценки ориентации фильтром на основе метода Калмана и предлагаемый фильтр оценки ориентации для реализаций с датчиком и без. Ошибки оцениваемых параметров Эйлера: φ, θ and ψ, были вычислены как разность между параметрами Эйлера калиброванных оптических измерений и соответствующими параметрами на выходе из фильтра.
5.1. Средние результаты
На рис. 7, 8 и 9 показаны средние результаты для 8 экспериментов как для фильтра на основе метода Калмана и предлагаемая реализация фильтра с магнитометром. В каждом рисунке 3 графика. Верхний график представляет оптически измеренный угол. Далее оценка угла фильтром на основе метода Калмана, и наконец оценка угла представляемым фильтром. Два графика внизу представляют расчётную ошибку в каждом из предлагаемых углов.
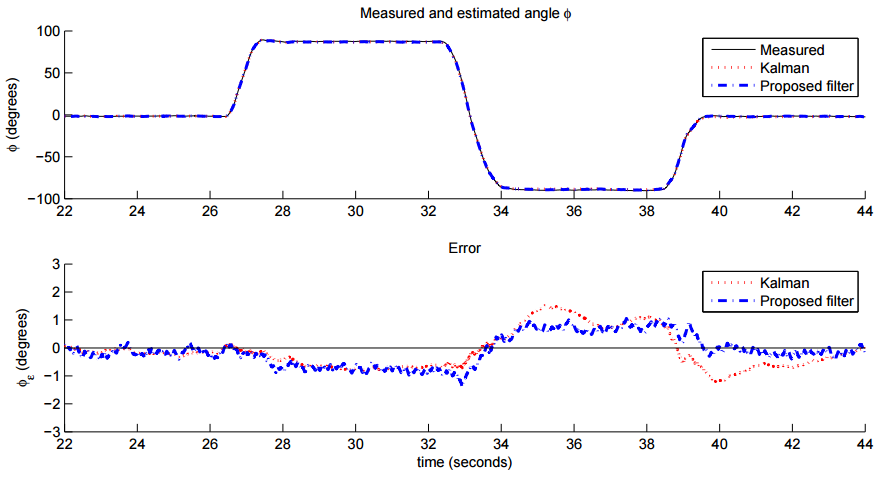
Рис 7. Средние результаты измерений и оценок угла φ (вверху) и ошибки оценки (внизу)

Рис 8. Средние результаты измерений и оценок угла θ (вверху) и ошибки оценки (внизу)
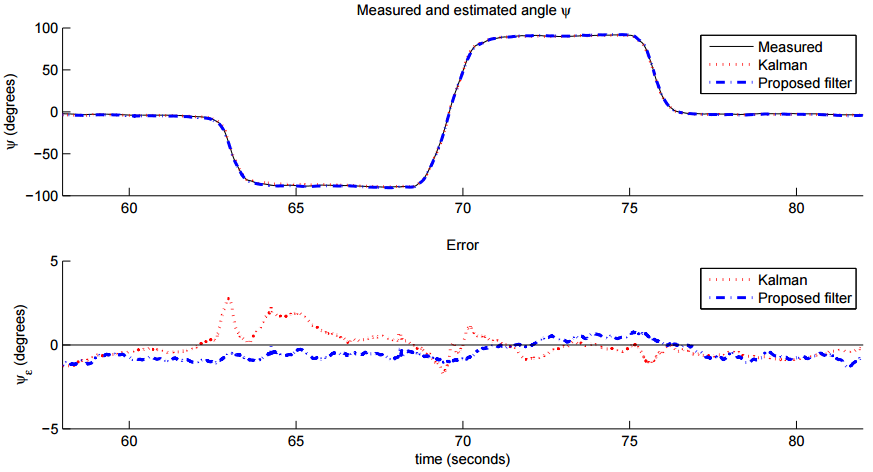
Рис 9. Средние результаты измерений и оценок угла ψ (вверху) и ошибки оценки (внизу)
5.2. Статические и динамические характеристики
Среднеквадратичные отклонения углов
 ,
, 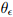 и
и  рассчитывались из предположения, что угловая скорость в неподвижном состоянии была < 5 ◦/сек, а в подвижном ≥ 5 ◦/сек.
рассчитывались из предположения, что угловая скорость в неподвижном состоянии была < 5 ◦/сек, а в подвижном ≥ 5 ◦/сек. Этот порог был выбран так, чтобы быть достаточно высоким по отношению к уровню шума входных данных. Каждое значение среднеквадратичного отклонения вычислялось в отрезок времени, в котором производились вращения соответствующего угла Эйлера, как показано на рис. 7, 8 и 9. Так было сделано, чтобы предотвратить ошибки из-за первоначального сближения или особенностей в представлении углов Эйлера, то есть когда θ = ± 90 (речь о складывании рамок). Результаты отражены в таблице 1. Каждое значение представляет собой среднее всех 8 экспериментов. Значения среднеквадратичного отклонения
 не вычислялись для реализации без магнитометра, так как данная реализация не предназначена для точного определения курса и не может его компенсировать накопление ошибок в этом параметре.
не вычислялись для реализации без магнитометра, так как данная реализация не предназначена для точного определения курса и не может его компенсировать накопление ошибок в этом параметре.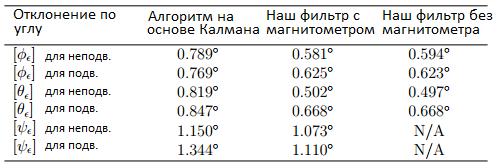
Таблица 1. Среднеквадратичные отклонения для фильтров: на основе метода Калмана и предложенного метода в реализациях с магнитометром и без
Результаты показывают, что предлагаемый фильтр достигает более высокой точности, чем фильтр на основе метода Калмана. Производители датчиков ориентации указывают средние отклонения фильтров на основе метода Калмана в пределах < 0.5◦ для углов φ и θ и < 1◦ для ψ [18]. Эти значения не соответствуют приведённым в таблице 1. Другие исследования [49] показали, что точность может быть значительно меньше, чем приведённые изготовителями и что указываемый ими уровень точности достигается только во время калибровки. Нмзкие уровни точности в измерении курса ψ вызваны низким уровнем точности датчика в измерении магнитного поля Земли. Наклон магнитного поля Земли во время тестирования был между 65◦ и 70◦ по отношению к горизонту [39]. Как следствие компонент вектора магнитного потока для определения курса относительно невелик. Больший компонент вектора, наряду с измерением гравитации, служит дополнительным критерием для определения крена θ и тангажа φ. Следовательно среднеквадратичное отклонение по тангажу
 и крену
и крену 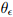 будет меньше, чем по курсу
будет меньше, чем по курсу  . Магнитометр, как указано в [18], имеет пропускную способность 10 Гц, которая по сравнению с пропускной способностью акселерометра и гироскопа, которая составляет от 30 до 40 Гц, также предполагает повышенную ошибку в определении курса
. Магнитометр, как указано в [18], имеет пропускную способность 10 Гц, которая по сравнению с пропускной способностью акселерометра и гироскопа, которая составляет от 30 до 40 Гц, также предполагает повышенную ошибку в определении курса  в неподвижном состоянии.
в неподвижном состоянии. 5.3. Влияние коэффициента усиления фильтра на точность
Результаты исследования влияния коэффициента усиления β на точность фильтра отображены в виде графика на рис. 10. Экспериментальные данные были обработаны ограничиваясь значениями β в пределах между 0 и 0,5. Для каждой реализации фильтра существует своё оптимальное значение β, которое достаточно высокое для того, чтобы компенсировать накопление ошибок и достаточно низкое, чтобы ненужный шум не попадал в большие шаги градиентного спуска.

Рис. 10. Влияние коэффициента усиления β фильтра на точность
5.4. Влияние частоты замеров на точность
На рис. 11 представлены результаты исследования влияния частоты замеров на точность фильтра. Эксперименты проводились, используя оптимальное значение коэффициента усиления β для обеих реализаций (с магнитометром и без). Изменение частоты замеров было сымитировано путём пропуска части замеров и составило от 1 Гц до 512 Гц. Из рис. 11 можно видеть, что предлагаемый фильтр достигает такого же уровня точности при частоте замеров 50 Гц, как при частоте 512 Гц. Обе реализации фильтра достигают снижение статической ошибки (в неподвижном состоянии) < 2◦ и динамической ошибки (в подвижном состоянии платформы) < 7◦ уже при частоте замеров 10 Гц. Этот уровень точности достаточен для использования в приложениях по захвату движений человека.

Рис. 11. Влияние частоты замеров на точность фильтра для реализаций с магнитометром и без
5.5. Дрейф нуля гироскопа
Калиброванные данные гироскопа, используемые в предлагаемом фильтре, не содержат каких-либо ошибок смещения. Чтобы исследовать способность предлагаемого фильтра в компенсации дрейфа смещения, ошибки были искусственно введены в данные всех 8 экспериментов. Постоянный дрейф 0.2◦/сек/сек был добавлен к замерам гироскопа по оси X
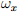 и постоянная ошибка смещения −0.2 ◦/сек/сек к замерам гироскопа по оси Y
и постоянная ошибка смещения −0.2 ◦/сек/сек к замерам гироскопа по оси Y  . Коэффициент усиления ζ выставлялся в 0 в течении первых 10 секунд во время каждого эксперимента, пока фильтр сходился с начальными условиями. После этого значение устанавливалось в 0,015 как соответствующее максимальной скорости смещения гироскопа 1◦/сек/сек. Рис. 12 показывает средние результаты 8 экспериментов, показывая смещения нуля гироскопа по оценкам фильтра от действительного положения по осям гироскопа X и Y. Точность фильтра в этих условиях описаны в таблице 1.
. Коэффициент усиления ζ выставлялся в 0 в течении первых 10 секунд во время каждого эксперимента, пока фильтр сходился с начальными условиями. После этого значение устанавливалось в 0,015 как соответствующее максимальной скорости смещения гироскопа 1◦/сек/сек. Рис. 12 показывает средние результаты 8 экспериментов, показывая смещения нуля гироскопа по оценкам фильтра от действительного положения по осям гироскопа X и Y. Точность фильтра в этих условиях описаны в таблице 1.
Рис. 12 Следящий фильтр дрейфа нуля гироскопа
6. Обсуждение
В начале работы над фильтром предполагалось, что акселерометр и магнитометр будут измерять только силу тяжести и магнитное поле Земли. На практике, из-за ускорений движения это приводит к ошибочному наблюдаемому направлению силы тяжести (особенно если перегрузка создаваемая движением соизмерима или больше величины силы тяжести), что даёт потенциально неправильную оценку высоты, а искажения магнитного поля дают неправильную оценку курса. Во многих реализациях фильтров авторы делают предположение, что ускорение движения и магнитные искажения присутствуют только короткий период времени. Поэтому величина коэффициента усиления фильтра β может быть выбрана достаточно низкой, чтобы отклонение вызванное ошибочными представлениями о гравитационных и магнитных искажениях наблюдаемых на местах, снизилось до приемлемого уровня за период. Минимально допустимое значение β ограничивается погрешностью измерений гироскопа.
Во многих приложениях может быть полезным использовать динамический прирост значений β и ζ. Это приведёт к снижению влияния акселерометра или магнитометра на оценку текущего положения во время проблемных периодов, например, при обнаружении большой перегрузки. Использование больших значений усиления фильтра во время инициализации может также улучшить сходимость фильтра в начальных условиях. Например, было установлено, что увеличение β и ζ на 10 позволяет за 5 секунд с момента включения фильтра компенсировать ошибку смещения гироскопа 1000 град / с в каждой оси.
Структура фильтра для установки решетки датчиков ИНС с магнитометром аналогична предложенной Бахманом и другими [34]. Обе реализации фильтра оценивают погрешность измерения гироскопа как градиент поверхности ошибок, созданной измерениями акселерометра и магнитометра. Фильтр Бахмана вычисляет это, используя подход Гаусса-Ньютона, который требует численного дифференцирования и инверсии матрицы. Фильтр, предлагаемый в настоящем докладе, использует аналитический вывод Якоби и работает на нормализованном градиенте поверхности ошибок. В результате, фильтр, предложенный в этой статье, предусматривает существенное сокращение вычислительной нагрузки и позволяет фильтру оптимально усиливать источник, основываясь на наблюдаемых характеристиках системы.
Экспериментальная процедура используемая для оценки точности фильтра имеет ряд ограничений. Фильтр не был оценен для одновременного вращения вокруг более чем одной оси и скорости вращения были ограничены по величине и по времени. Эти ограничения были необходимы, чтобы была возможна повторяемость и количественная оценка.
7. Выводы
По сути повтор текста из введения.
Приложение А. Реализация фильтра на С без магнитометра
Следующий исходный код является реализацией фильтра ориентации без магнитометра. С.-код был оптимизирован чтобы минимизировать необходимое количество арифметических операций за счет оперативной памяти. На каждое обновление фильтра требуется 109 скалярных арифметических операций (18 операций сложения, 20 вычитания, 57 умножений, 11 делений и 3 получения квадратного корня).Реализация требует 40 байт оперативной памяти для глобальных переменных и 100 байт оперативной памяти для локальных переменных во время каждого вызова функции обновления фильтра.
Приложение А. Реализация фильтра на С без магнитометра
// Math library required for ‘sqrt’
#include <math.h>
// System constants
#define deltat 0.001f // sampling period in seconds (shown as 1 ms)
#define gyroMeasError 3.14159265358979f * (5.0f / 180.0f) // gyroscope measurement error in rad/s (shown as 5 deg/s)
#define beta sqrt(3.0f / 4.0f) * gyroMeasError // compute beta
// Global system variables
float a_x, a_y, a_z; // accelerometer measurements
float w_x, w_y, w_z; // gyroscope measurements in rad/s
float SEq_1 = 1.0f, SEq_2 = 0.0f, SEq_3 = 0.0f, SEq_4 = 0.0f; // estimated orientation quaternion elements with initial conditions
void filterUpdate(float w_x, float w_y, float w_z, float a_x, float a_y, float a_z)
{
// Local system variables
float norm; // vector norm
float SEqDot_omega_1, SEqDot_omega_2, SEqDot_omega_3, SEqDot_omega_4; // quaternion derrivative from gyroscopes elements
float f_1, f_2, f_3; // objective function elements
float J_11or24, J_12or23, J_13or22, J_14or21, J_32, J_33; // objective function Jacobian elements
float SEqHatDot_1, SEqHatDot_2, SEqHatDot_3, SEqHatDot_4; // estimated direction of the gyroscope error
// Axulirary variables to avoid reapeated calcualtions
float halfSEq_1 = 0.5f * SEq_1;
float halfSEq_2 = 0.5f * SEq_2;
float halfSEq_3 = 0.5f * SEq_3;
float halfSEq_4 = 0.5f * SEq_4;
float twoSEq_1 = 2.0f * SEq_1;
float twoSEq_2 = 2.0f * SEq_2;
float twoSEq_3 = 2.0f * SEq_3;
// Normalise the accelerometer measurement
norm = sqrt(a_x * a_x + a_y * a_y + a_z * a_z);
a_x /= norm;
a_y /= norm;
a_z /= norm;
// Compute the objective function and Jacobian
f_1 = twoSEq_2 * SEq_4 - twoSEq_1 * SEq_3 - a_x;
f_2 = twoSEq_1 * SEq_2 + twoSEq_3 * SEq_4 - a_y;
f_3 = 1.0f - twoSEq_2 * SEq_2 - twoSEq_3 * SEq_3 - a_z;
J_11or24 = twoSEq_3; // J_11 negated in matrix multiplication
J_12or23 = 2.0f * SEq_4;
J_13or22 = twoSEq_1; // J_12 negated in matrix multiplication
J_14or21 = twoSEq_2;
J_32 = 2.0f * J_14or21; // negated in matrix multiplication
J_33 = 2.0f * J_11or24; // negated in matrix multiplication
// Compute the gradient (matrix multiplication)
SEqHatDot_1 = J_14or21 * f_2 - J_11or24 * f_1;
SEqHatDot_2 = J_12or23 * f_1 + J_13or22 * f_2 - J_32 * f_3;
SEqHatDot_3 = J_12or23 * f_2 - J_33 * f_3 - J_13or22 * f_1;
SEqHatDot_4 = J_14or21 * f_1 + J_11or24 * f_2;
// Normalise the gradient
norm = sqrt(SEqHatDot_1 * SEqHatDot_1 + SEqHatDot_2 * SEqHatDot_2 + SEqHatDot_3 * SEqHatDot_3 + SEqHatDot_4 * SEqHatDot_4);
SEqHatDot_1 /= norm;
SEqHatDot_2 /= norm;
SEqHatDot_3 /= norm;
SEqHatDot_4 /= norm;
// Compute the quaternion derrivative measured by gyroscopes
SEqDot_omega_1 = -halfSEq_2 * w_x - halfSEq_3 * w_y - halfSEq_4 * w_z;
SEqDot_omega_2 = halfSEq_1 * w_x + halfSEq_3 * w_z - halfSEq_4 * w_y;
SEqDot_omega_3 = halfSEq_1 * w_y - halfSEq_2 * w_z + halfSEq_4 * w_x;
SEqDot_omega_4 = halfSEq_1 * w_z + halfSEq_2 * w_y - halfSEq_3 * w_x;
// Compute then integrate the estimated quaternion derrivative
SEq_1 += (SEqDot_omega_1 - (beta * SEqHatDot_1)) * deltat;
SEq_2 += (SEqDot_omega_2 - (beta * SEqHatDot_2)) * deltat;
SEq_3 += (SEqDot_omega_3 - (beta * SEqHatDot_3)) * deltat;
SEq_4 += (SEqDot_omega_4 - (beta * SEqHatDot_4)) * deltat;
// Normalise quaternion
norm = sqrt(SEq_1 * SEq_1 + SEq_2 * SEq_2 + SEq_3 * SEq_3 + SEq_4 * SEq_4);
SEq_1 /= norm;
SEq_2 /= norm;
SEq_3 /= norm;
SEq_4 /= norm;
}
Приложение А. Реализация фильтра на С с магнитометром
Следующий исходный код является реализацией фильтра ориентации с магнитометром и системой компенсации дрейфа гироскопа. С.-код был оптимизирован чтобы минимизировать необходимое количество арифметических операций за счет оперативной памяти. На каждое обновление фильтра требуется 277 скалярных арифметических операций (51 операция сложения, 57 вычитания, 155 умножений, 14 делений и 5 получений квадратного корня).Реализация требует 72 байта оперативной памяти для глобальных переменных и 260 байт оперативной памяти для локальных переменных во время каждого вызова функции обновления фильтра.
Приложение Б. Реализация фильтра на С с магнитометром
// Math library required for ‘sqrt’
#include <math.h>
// System constants
#define deltat 0.001f // sampling period in seconds (shown as 1 ms)
#define gyroMeasError 3.14159265358979 * (5.0f / 180.0f) // gyroscope measurement error in rad/s (shown as 5 deg/s)
#define gyroMeasDrift 3.14159265358979 * (0.2f / 180.0f) // gyroscope measurement error in rad/s/s (shown as 0.2f deg/s/s)
#define beta sqrt(3.0f / 4.0f) * gyroMeasError // compute beta
#define zeta sqrt(3.0f / 4.0f) * gyroMeasDrift // compute zeta
// Global system variables
float a_x, a_y, a_z; // accelerometer measurements
float w_x, w_y, w_z; // gyroscope measurements in rad/s
float m_x, m_y, m_z; // magnetometer measurements
float SEq_1 = 1, SEq_2 = 0, SEq_3 = 0, SEq_4 = 0; // estimated orientation quaternion elements with initial conditions
float b_x = 1, b_z = 0; // reference direction of flux in earth frame
float w_bx = 0, w_by = 0, w_bz = 0; // estimate gyroscope biases error
// Function to compute one filter iteration
void filterUpdate(float w_x, float w_y, float w_z, float a_x, float a_y, float a_z, float m_x, float m_y, float m_z)
{
// local system variables
float norm; // vector norm
float SEqDot_omega_1, SEqDot_omega_2, SEqDot_omega_3, SEqDot_omega_4; // quaternion rate from gyroscopes elements
float f_1, f_2, f_3, f_4, f_5, f_6; // objective function elements
float J_11or24, J_12or23, J_13or22, J_14or21, J_32, J_33, // objective function Jacobian elements
J_41, J_42, J_43, J_44, J_51, J_52, J_53, J_54, J_61, J_62, J_63, J_64; //
float SEqHatDot_1, SEqHatDot_2, SEqHatDot_3, SEqHatDot_4; // estimated direction of the gyroscope error
float w_err_x, w_err_y, w_err_z; // estimated direction of the gyroscope error (angular)
float h_x, h_y, h_z; // computed flux in the earth frame
// axulirary variables to avoid reapeated calcualtions
float halfSEq_1 = 0.5f * SEq_1;
float halfSEq_2 = 0.5f * SEq_2;
float halfSEq_3 = 0.5f * SEq_3;
float halfSEq_4 = 0.5f * SEq_4;
float twoSEq_1 = 2.0f * SEq_1;
float twoSEq_2 = 2.0f * SEq_2;
float twoSEq_3 = 2.0f * SEq_3;
float twoSEq_4 = 2.0f * SEq_4;
float twob_x = 2.0f * b_x;
float twob_z = 2.0f * b_z;
float twob_xSEq_1 = 2.0f * b_x * SEq_1;
float twob_xSEq_2 = 2.0f * b_x * SEq_2;
float twob_xSEq_3 = 2.0f * b_x * SEq_3;
float twob_xSEq_4 = 2.0f * b_x * SEq_4;
float twob_zSEq_1 = 2.0f * b_z * SEq_1;
float twob_zSEq_2 = 2.0f * b_z * SEq_2;
float twob_zSEq_3 = 2.0f * b_z * SEq_3;
float twob_zSEq_4 = 2.0f * b_z * SEq_4;
float SEq_1SEq_2;
float SEq_1SEq_3 = SEq_1 * SEq_3;
float SEq_1SEq_4;
float SEq_2SEq_3;
float SEq_2SEq_4 = SEq_2 * SEq_4;
float SEq_3SEq_4;
float twom_x = 2.0f * m_x;
float twom_y = 2.0f * m_y;
float twom_z = 2.0f * m_z;
// normalise the accelerometer measurement
norm = sqrt(a_x * a_x + a_y * a_y + a_z * a_z);
a_x /= norm;
a_y /= norm;
a_z /= norm;
// normalise the magnetometer measurement
norm = sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
m_x /= norm;
m_y /= norm;
m_z /= norm;
// compute the objective function and Jacobian
f_1 = twoSEq_2 * SEq_4 - twoSEq_1 * SEq_3 - a_x;
f_2 = twoSEq_1 * SEq_2 + twoSEq_3 * SEq_4 - a_y;
f_3 = 1.0f - twoSEq_2 * SEq_2 - twoSEq_3 * SEq_3 - a_z;
f_4 = twob_x * (0.5f - SEq_3 * SEq_3 - SEq_4 * SEq_4) + twob_z * (SEq_2SEq_4 - SEq_1SEq_3) - m_x;
f_5 = twob_x * (SEq_2 * SEq_3 - SEq_1 * SEq_4) + twob_z * (SEq_1 * SEq_2 + SEq_3 * SEq_4) - m_y;
f_6 = twob_x * (SEq_1SEq_3 + SEq_2SEq_4) + twob_z * (0.5f - SEq_2 * SEq_2 - SEq_3 * SEq_3) - m_z;
J_11or24 = twoSEq_3; // J_11 negated in matrix multiplication
J_12or23 = 2.0f * SEq_4;
J_13or22 = twoSEq_1; // J_12 negated in matrix multiplication
J_14or21 = twoSEq_2;
J_32 = 2.0f * J_14or21; // negated in matrix multiplication
J_33 = 2.0f * J_11or24; // negated in matrix multiplication
J_41 = twob_zSEq_3; // negated in matrix multiplication
J_42 = twob_zSEq_4;
J_43 = 2.0f * twob_xSEq_3 + twob_zSEq_1; // negated in matrix multiplication
J_44 = 2.0f * twob_xSEq_4 - twob_zSEq_2; // negated in matrix multiplication
J_51 = twob_xSEq_4 - twob_zSEq_2; // negated in matrix multiplication
J_52 = twob_xSEq_3 + twob_zSEq_1;
J_53 = twob_xSEq_2 + twob_zSEq_4;
J_54 = twob_xSEq_1 - twob_zSEq_3; // negated in matrix multiplication
J_61 = twob_xSEq_3;
J_62 = twob_xSEq_4 - 2.0f * twob_zSEq_2;
J_63 = twob_xSEq_1 - 2.0f * twob_zSEq_3;
J_64 = twob_xSEq_2;
// compute the gradient (matrix multiplication)
SEqHatDot_1 = J_14or21 * f_2 - J_11or24 * f_1 - J_41 * f_4 - J_51 * f_5 + J_61 * f_6;
SEqHatDot_2 = J_12or23 * f_1 + J_13or22 * f_2 - J_32 * f_3 + J_42 * f_4 + J_52 * f_5 + J_62 * f_6;
SEqHatDot_3 = J_12or23 * f_2 - J_33 * f_3 - J_13or22 * f_1 - J_43 * f_4 + J_53 * f_5 + J_63 * f_6;
SEqHatDot_4 = J_14or21 * f_1 + J_11or24 * f_2 - J_44 * f_4 - J_54 * f_5 + J_64 * f_6;
// normalise the gradient to estimate direction of the gyroscope error
norm = sqrt(SEqHatDot_1 * SEqHatDot_1 + SEqHatDot_2 * SEqHatDot_2 + SEqHatDot_3 * SEqHatDot_3 + SEqHatDot_4 * SEqHatDot_4);
SEqHatDot_1 = SEqHatDot_1 / norm;
SEqHatDot_2 = SEqHatDot_2 / norm;
SEqHatDot_3 = SEqHatDot_3 / norm;
SEqHatDot_4 = SEqHatDot_4 / norm;
// compute angular estimated direction of the gyroscope error
w_err_x = twoSEq_1 * SEqHatDot_2 - twoSEq_2 * SEqHatDot_1 - twoSEq_3 * SEqHatDot_4 + twoSEq_4 * SEqHatDot_3;
w_err_y = twoSEq_1 * SEqHatDot_3 + twoSEq_2 * SEqHatDot_4 - twoSEq_3 * SEqHatDot_1 - twoSEq_4 * SEqHatDot_2;
w_err_z = twoSEq_1 * SEqHatDot_4 - twoSEq_2 * SEqHatDot_3 + twoSEq_3 * SEqHatDot_2 - twoSEq_4 * SEqHatDot_1;
// compute and remove the gyroscope baises
w_bx += w_err_x * deltat * zeta;
w_by += w_err_y * deltat * zeta;
w_bz += w_err_z * deltat * zeta;
w_x -= w_bx;
w_y -= w_by;
w_z -= w_bz;
// compute the quaternion rate measured by gyroscopes
SEqDot_omega_1 = -halfSEq_2 * w_x - halfSEq_3 * w_y - halfSEq_4 * w_z;
SEqDot_omega_2 = halfSEq_1 * w_x + halfSEq_3 * w_z - halfSEq_4 * w_y;
SEqDot_omega_3 = halfSEq_1 * w_y - halfSEq_2 * w_z + halfSEq_4 * w_x;
SEqDot_omega_4 = halfSEq_1 * w_z + halfSEq_2 * w_y - halfSEq_3 * w_x;
// compute then integrate the estimated quaternion rate
SEq_1 += (SEqDot_omega_1 - (beta * SEqHatDot_1)) * deltat;
SEq_2 += (SEqDot_omega_2 - (beta * SEqHatDot_2)) * deltat;
SEq_3 += (SEqDot_omega_3 - (beta * SEqHatDot_3)) * deltat;
SEq_4 += (SEqDot_omega_4 - (beta * SEqHatDot_4)) * deltat;
// normalise quaternion
norm = sqrt(SEq_1 * SEq_1 + SEq_2 * SEq_2 + SEq_3 * SEq_3 + SEq_4 * SEq_4);
SEq_1 /= norm;
SEq_2 /= norm;
SEq_3 /= norm;
SEq_4 /= norm;
// compute flux in the earth frame
SEq_1SEq_2 = SEq_1 * SEq_2; // recompute axulirary variables
SEq_1SEq_3 = SEq_1 * SEq_3;
SEq_1SEq_4 = SEq_1 * SEq_4;
SEq_3SEq_4 = SEq_3 * SEq_4;
SEq_2SEq_3 = SEq_2 * SEq_3;
SEq_2SEq_4 = SEq_2 * SEq_4;
h_x = twom_x * (0.5f - SEq_3 * SEq_3 - SEq_4 * SEq_4) + twom_y * (SEq_2SEq_3 - SEq_1SEq_4) + twom_z * (SEq_2SEq_4 + SEq_1SEq_3);
h_y = twom_x * (SEq_2SEq_3 + SEq_1SEq_4) + twom_y * (0.5f - SEq_2 * SEq_2 - SEq_4 * SEq_4) + twom_z * (SEq_3SEq_4 - SEq_1SEq_2);
h_z = twom_x * (SEq_2SEq_4 - SEq_1SEq_3) + twom_y * (SEq_3SEq_4 + SEq_1SEq_2) + twom_z * (0.5f - SEq_2 * SEq_2 - SEq_3 * SEq_3);
// normalise the flux vector to have only components in the x and z
b_x = sqrt((h_x * h_x) + (h_y * h_y));
b_z = h_z;
}
Список литературы
- Mark Euston, Paul Coote, Robert Mahony, Jonghyuk Kim, and Tarek Hamel. A complementary filter for attitude estimation of a fixed-wing uav with a low-cost imu. In 6th International Conference on Field and Service Robotics, July 2007.
- Sung Kyung Hong. Fuzzy logic based closed-loop strapdown attitude system for unmanned aerial vehicle (uav). Sensors and Actuators A: Physical, 107(2):109 – 118, 2003.
- A. Kallapur, I. Petersen, and S. Anavatti. A robust gyroless attitude estimation scheme for a small fixed-wing unmanned aerial vehicle. pages 666 –671, aug. 2009.
- B. Barshan and H. F. Durrant-Whyte. Inertial navigation systems for mobile robots. 11(3):328–342, June 1995.
- L. Ojeda and J. Borenstein. Flexnav: fuzzy logic expert rule-based position estimation for mobile robots on rugged terrain. In Proc. IEEE International Conference on Robotics and Automation ICRA ’02, volume 1, pages 317–322, May 11–15, 2002.
- David H. Titterton and John L. Weston. Strapdown inertial navigation technology. The Institution of Electrical Engineers, 2004.
- S. Beauregard. Omnidirectional pedestrian navigation for first responders. In Proc. 4th Workshop on Positioning, Navigation and Communication WPNC ’07, pages 33–36, March 22–22, 2007.
- H. J. Luinge and P. H. Veltink. Inclination measurement of human movement using a 3-d accelerometer with autocalibration. 12(1):112–121, March 2004. [9] Huiyu Zhou and Huosheng Hu. Human motion tracking for rehabilitation–a survey. volume 3, pages 1 – 18, 2008.
- E. A. Heinz, K. S. Kunze, M. Gruber, D. Bannach, and P. Lukowicz. Using wearable sensors for real-time recognition tasks in games of martial arts — an initial experiment. In Proc. IEEE Symposium on Computational Intelligence and Games, pages 98–102, May 22–24, 2006.
- J. E. Bortz. A new mathematical formulation for strapdown inertial navigation. (1):61– 66, January 1971.
- M B Ignagni. Optimal strapdown attitude integration algorithms. In Guidance, Control, and Dynamics, volume 13, pages 363–369, 1990.
- N. Yazdi, F. Ayazi, and K. Najafi. Micromachined inertial sensors. 86(8):1640–1659, August 1998.
- R. E. Kalman. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82:35–45, 1960.
- E. Foxlin. Inertial head-tracker sensor fusion by a complementary separate-bias kalman filter. In Proc. Virtual Reality Annual International Symposium the IEEE 1996, pages 185–194,267, March 30–April 3, 1996.
- H. J. Luinge, P. H. Veltink, and C. T. M. Baten. Estimation of orientation with gyroscopes and accelerometers. In Proc. First Joint [Engineering in Medicine and Biology 21st Annual Conf. and the 1999 Annual Fall Meeting of the Biomedical Engineering Soc.] BMES/EMBS Conference, volume 2, page 844, October 13–16, 1999.
- J. L. Marins, Xiaoping Yun, E. R. Bachmann, R. B. McGhee, and M. J. Zyda. An extended kalman filter for quaternion-based orientation estimation using marg sensors. In Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems, volume 4, pages 2003–2011, October 29–November 3, 2001.
- Xsens Technologies B.V. MTi and MTx User Manual and Technical Documentation. Pantheon 6a, 7521 PR Enschede, The Netherlands, May 2009.
- MicroStrain Inc. 3DM-GX3 -25 Miniature Attutude Heading Reference Sensor. 459 Hurricane Lane, Suite 102, Williston, VT 05495 USA, 1.04 edition, 2009.
- VectorNav Technologies, LLC. VN -100 User Manual. College Station, TX 77840 USA, preliminary edition, 2009.
- InterSense, Inc. InertiaCube2+ Manual. 36 Crosby Drive, Suite 150, Bedford, MA 01730, USA, 1.0 edition, 2008.
- PNI sensor corporation. Spacepoint Fusion. 133 Aviation Blvd, Suite 101, Santa Rosa, CA 95403-1084 USA.
- Crossbow Technology, Inc. AHRS400 Series Users Manual. 4145 N. First Street, San Jose, CA 95134, rev. c edition, February 2007.
- A. M. Sabatini. Quaternion-based extended kalman filter for determining orientation by inertial and magnetic sensing. 53(7):1346–1356, July 2006.
- H. J. Luinge and P. H. Veltink. Measuring orientation of human body segments using miniature gyroscopes and accelerometers. Medical and Biological Engineering and Computing, 43(2):273–282, April 2006.
- David Jurman, Marko Jankovec, Roman Kamnik, and Marko Topic. Calibration and data fusion solution for the miniature attitude and heading reference system. Sensors and Actuators A: Physical, 138(2):411–420, August 2007.
- Markus Haid and Jan Breitenbach. Low cost inertial orientation tracking with kalman filter. Applied Mathematics and Computation, 153(4):567 575, June 2004.
- D. Roetenberg, H. J. Luinge, C. T. M. Baten, and P. H. Veltink. Compensation of magnetic disturbances improves inertial and magnetic sensing of human body segment orientation. 13(3):395–405, September 2005.
- John L. Crassidis and Landis F. Markley. Unscented filtering for spacecraft attitude estimation. Journal of guidance, control, and dynamics, 26(4):536–542, 2003.
- D. Gebre-Egziabher, R.C. Hayward, and J.D. Powell. Design of multi-sensor attitude determination systems. Aerospace and Electronic Systems, IEEE Transactions on, 40(2):627 – 649, april 2004.
- N.H.Q. Phuong, H.-J. Kang, Y.-S. Suh, and Y.-S. Ro. A DCM based orientation estimation algorithm with an inertial measurement unit and a magnetic compass. Journal of Universal Computer Science, 15(4):859–876, 2009.
- Daniel Choukroun. Novel methods for attitude determination using vector observations. PhD thesis, Israel Institute of Technology, May 2003.
- R. A. Hyde, L. P. Ketteringham, S. A. Neild, and R. J. S. Jones. Estimation of upperlimb orientation based on accelerometer and gyroscope measurements. 55(2):746–754, February 2008.
- E. R. Bachmann, I. Duman, U. Y. Usta, R. B. McGhee, X. P. Yun, and M. J. Zyda. Orientation tracking for humans and robots using inertial sensors. In Proc. IEEE International Symposium on Computational Intelligence in Robotics and Automation CIRA
- ’99, pages 187–194, November 8–9, 1999.
- R. Mahony, T. Hamel, and J.-M. Pflimlin. Nonlinear complementary filters on the special orthogonal group. Automatic Control, IEEE Transactions on, 53(5):1203 –1218, june 2008.
- J. B. Kuipers. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace and Virtual Reality. Princeton University Press, 1999.
- John J. Craig. Introduction to Robotics Mechanics and Control. Pearson Education International, 2005.
- David R. Pratt Robert B. McGhee Joseph M. Cooke, Michael J. Zyda. Npsnet: Flight simulation dynamic modelling using quaternions. Presence, 1:404–420, 1994.
- John Arthur Jacobs. The earth’s core, volume 37 of International geophysics series. Academic Press, 2 edition, 1987.
- E. R. Bachmann, Xiaoping Yun, and C. W. Peterson. An investigation of the effects of magnetic variations on inertial/magnetic orientation sensors. In Proc. IEEE International Conference on Robotics and Automation ICRA ’04, volume 2, pages 1115–1122, April 2004.
- C.T.M. Baten F.C.T. van der Helm W.H.K. de Vries, H.E.J. Veeger. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait & Posture, 29(4):535–541, 2009.
- Speake & Co Limited. Autocalibration algorithms for FGM type sensors. Application note.
- Michael J. Caruso. Applications of Magnetoresistive Sensors in Navigation Systems. Honeywell Inc., Solid State Electronics Center, Honeywell Inc. 12001 State Highway 55, Plymouth, MN 55441.
- J. F. Vasconcelos, G. Elkaim, C. Silvestre, P. Oliveira, and B. Cardeira. A geometric approach to strapdown magnetometer calibration in sensor frame. In Navigation, Guidance and Control of Underwater Vehicles, volume 2, 2008.
- Demoz Gebre-Egziabher, Gabriel H. Elkaim, J. David Powell, and Bradford W. Parkinson. Calibration of strapdown magnetometers in magnetic field domain. Journal of Aerospace Engineering, 19(2):87–102, 2006.
- Vicon Motion Systems Limited. Vicon MX Hardware. 5419 McConnell Avenue, Los Angeles, CA 90066, USA, 1.6 edition, 2004.
- Vicon Motion Systems Limited. Vicon Nexus Product Guide — Foundation Notes. 5419 McConnell Avenue, Los Angeles, CA 90066, USA, 1.2 edition, November 2007.
- Itzhack Y Bar-Itzhack. New method for extracting the quaternion from a rotation matrix. AIAA Journal of Guidance, Control and Dynamics, 23(6):10851087, Nov.Dec 2000. (Engineering Note).
- M. A. Brodie, A. Walmsley, and W. Page. The static accuracy and calibration of inertial measurement units for 3D orientation. Computer Methods in Biomechanics and Biomedical Engineering, 11(6):641–648, December 2008.