
Обнаружение столкновений (collision detection) виртуальных объектов является довольно значимой частью для задач визуализации.
Задача
А задача состоит в том, чтобы определить столкнулись (collide) ли два объекта или нет.
Сложность же состоит в том, что при тестировании примитивов визуализации непосредственно с другими примитивами вычисление коллизий занимает неоправданно большие ресурсы, особенно при огромном количестве объектов участвующих в симуляции.
Чтобы облегчить подобные вычисления и не производить проверку непосредственно между примитивами визуализации (что занимает наибольшее время), были выдуманы технологии ограничивающих объемов (bounding volume), которые позволяют описывать объекты визуализации таким образом, чтобы проверка на столкновения занимала не такие значительные ресурсы хотя и при небольшой потери точности.
Другими словами, ограничивающие объемы — это простые геометрические фигуры, куда вписываются более сложные объекты.
Bounding volumes
Наиболее востребованные ограничивающие объемы:
— Сфера (Sphere).
— Ограничивающий параллелепипед, выровненный по координатным осям (Axis-aligned bounding boxes — AABB, уж простите за перевод).
— Объектно-ориентированный ограничивающий параллелепипед (Object-oriented bounding boxes — OBB)
— Дискретно-ориентированные многогранники. (Discrete oriented polytopes — k-DOPs)
— и другие.
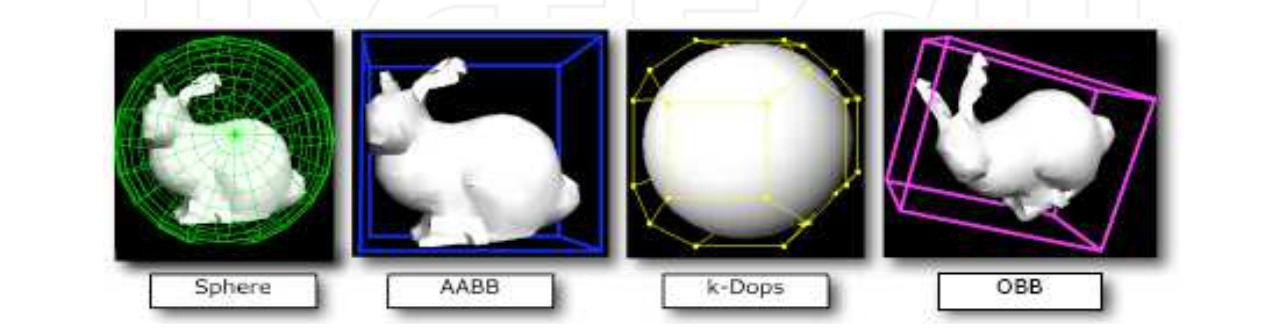
Рис 1. Обзор BV.
k-DOP
Каждый из них имеют ряд достоинств и недостатков, но остановимся на k-DOP.

Рис 2. Доходчиво о BV.
Дискретно-ориентированные многогранники — это заранее известное количество ограничивающих плоскостей и их ориентации. K в названии описывает количество таких плоскостей.
Например, двухмерный 4-DOP является обычным квадратом, описывающим некий также двухмерный объект. По сути AABB — это частный случай k-DOP.
Двухмерный AABB является таким же квадратом, как и 4-DOP.
А трехмерный AABB является таким же кубом, как и 6-DOP.
Но k-DOP так же может использовать большее количество плоскостей. И, как было сказано, ориентация таких плоскостей выбирается заранее и не меняется.
Ориентации плоскостей определяют через вектора направления, компоненты нормалей которых ограничены множеством {-1, 0, 1}.
Например, для обычного квадрата необходимо 4 плоскости с направлениями: (0, 1), (1, 0).
Здесь описаны направления двух плоскостей, но которые ограничивают квадрат снизу, сверху, слева и справа. Хотя всего плоскостей 4, поэтому, бывает, пишут еще так: (0, ±1), (±1, 0)
Данные нормали позволяют серьезно облегчить вычисления.
Структура
k-DOP описывается всего лишь минимальными и максимальными интервалами (slabs) или дистанциями. Два значения на одну плоскость, что в итоге получается довольно просто обрабатывать и хранить.
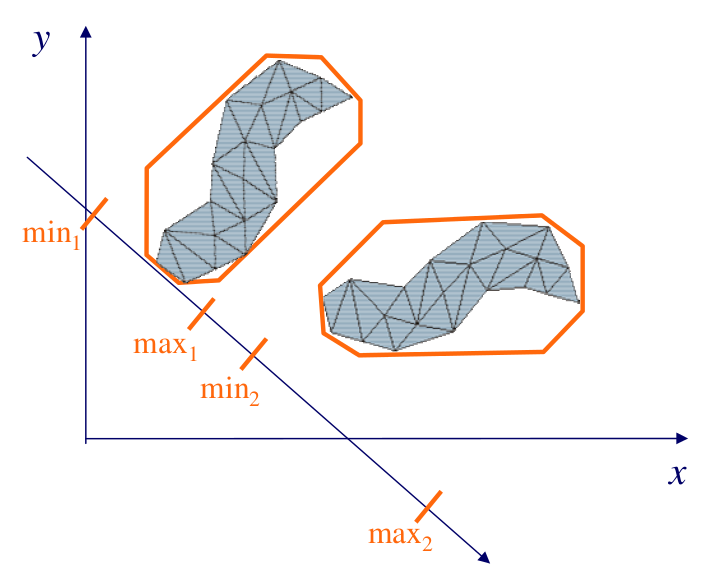
Рис 3. Интервалы в k-DOP.
Например, для квадрата, как мы запомнили, надо 4 плоскости (k=4). Значит, потребуется 2 (k/2) минимальных и 2 максимальных значений.
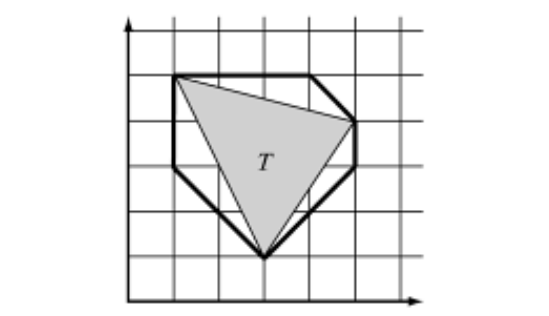
Рис 4. 8-DOP описывающий треугольник.
На рисунке №4 треугольник с координатами (3, 1), (5, 4), (1, 5) описан с помощью 8-DOP, т. е. восемью плоскостями и с векторами направления (1, 0), (0, 1), (1, 1), (1, -1).
Давайте посчитаем интервалы, описывающие этот многогранник.
Берем первую плоскость с направлением (1, 0) и умножаем на координаты:
3*1 + 1*0 = 3
5*1 + 4*0 = 5
1*1 + 5*0 = 1
Минимальное значение здесь 1, а максимальное 5.
Плоскость (1, 0) определяется значениями 1 и 5.
Для плоскости (0, 1) такие же значения 1 и 5.
Для (1, 1) — 4 и 9.
Для (1, -1) — -4 и 2.
Проверка на пересечение
Если по крайней мере одна плоскость не пересекается, то вся структура также не пересекается.
Только если все интервалы/плоскости пересекаются, тогда пересекается сама структура k-DOP. Но следует заметить, что описываемый объект может и не пересекаться.
Поэтому говорится, если k-DOP структуры двух объектов сталкиваются (collide), то их описываемые объекты могут сталкиваться.
bool overlapped(const KDop& a, const KDop& b, unsigned k)
{
for (unsigned i = 0; i < k / 2; ++i)
{
if (a.min[i] > b.max[i] || a.max[i] < b.min[i])
{
return false;
}
}
return true;
}
Иерархии ограничивающих объемов (Bounding Volume Hierarchy)
Как выяснилось, использование ограничивающих объемов позволяет упростить проверку на столкновения, но теряет немного в точности.
Поэтому для простых объектов, чтобы исключить не нужные проверки, тестируют сначала их ограничивающие объемы, как AABB или k-DOP, а после уже переходят на примитивы.
Но при сложно структурированных объектах применяют иерархии ограничивающих объемов. Часто это просто бинарные деревья, где ноды определяют какой-то объект или часть объекта, ограниченный каким-то объемом.

Рис 5. Дерево объектов.
Использование таких деревьев нужно для снижения количества вычислений.
Очевидно, что если проверку на коллизии производить непосредственно на объектах, это может потребовать слишком много времени. Применение ограничивающих объемов позволяет немного облегчить это задачу. А объединение ограничивающих объемов в иерархическую систему дает возможность исключить заведомо непересекающиеся части объекта.
Обычно создание дерева происходит одним способом из трех.
Сложный объект (рутовая нода) делится на менее сложные (дочерние ноды). Например, пока объекты не закончатся или пока не выполнится какое-то условие. (top down method)
Простые объекты (ноды) объединяются в более сложные пока не останется один сложный рутовый объект (bottom up method).
Или добавление объекта в уже сформированное дерево (insertion method).
При сбалансированном таком дереве сложность поиска равна сложности других сбалансированных бинарных деревьях поиска — O(logN).
Наиболее интересный вопрос каким же способом делить объект на дочерние.
Критерий сравнения частей объекта, чтобы помещать в левое или правое поддерево могут различаться.
Наиболее простым является простое деление пространства пополам: все объекты с координатами выше определенной идут в правое поддерево, все остальные в левое.
Также может быть подсчет среднего значения, например, по выбранной оси.
Или построение медианы. Или любым другим способом.
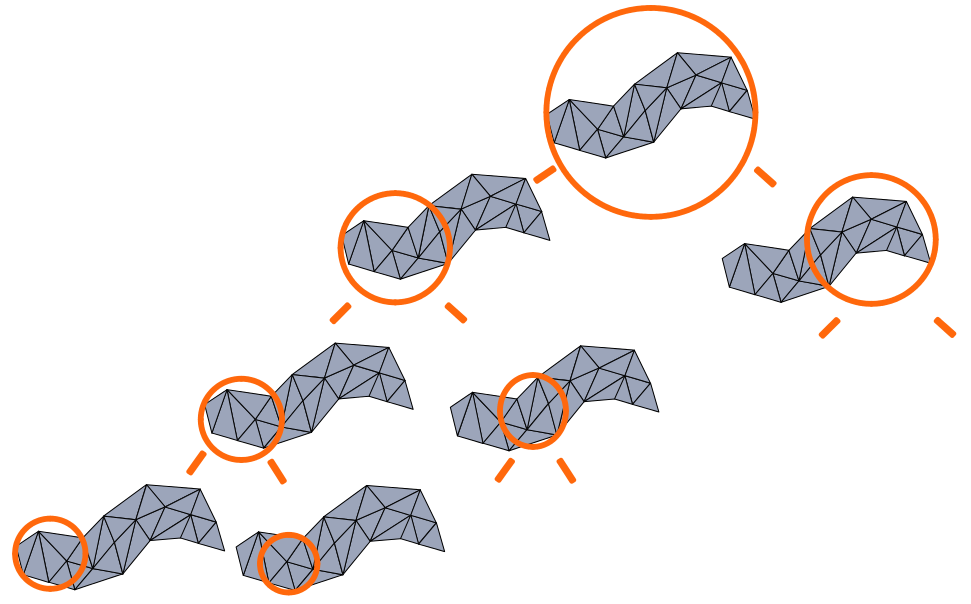
Рис 6. Другое абстрактное дерево объектов.
Поиск коллизий
Поиск столкновений на двух иерархических структур, в свою очередь, тоже может быть реализован разными способами.
Чтобы проверить на пересечения двух объектов, необходимо просто создать дерево (BVH-tree) на каждый объект, где нода определяет свою часть объекта через какой-то ограничивающий объем.
Далее нужно пройтись по деревьям и сопоставить ноду с одного дерева с нодами другого, таким образом, чтобы двигаться только в том направлении, где есть пересечение их ограничивающих объемов.
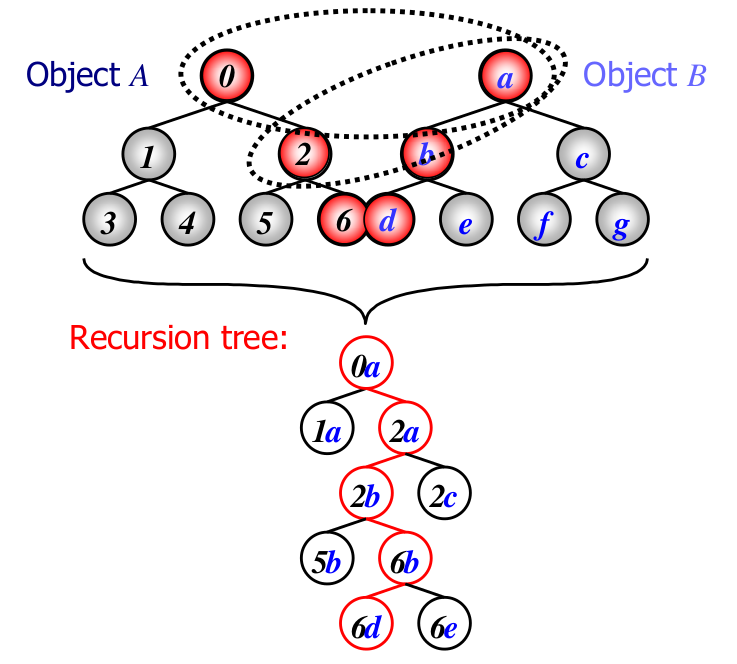
Рис 7. Дерево рекурсии сопоставления объектов.
Иллюстрации и информация
1. Christer Ericson. Real-Time Collision Detection, Volume 1. — Треугольничек и полезный абзац про многогранники.
2. Hamzah Asyrani Sulaiman and Abdullah Bade. Bounding Volume Hierarchies for Collision Detection. — Экскаватор, зайчик и совсем просто про коллизии, иерархии.
3. Johannes Mezger. Collision Handling in Dynamic Simulation Environments: Bounding Volume Hierarchies. — Дерево и интервалы многогранников. Коротко и тезисно про основные вопросы иерархических структур ограничивающих объемов.
4. Rolf Lakaemper. Game Programming. Introduction To Collision Detection — Титульное завлекалово и шедевр с человечками. Простой обзор по определению коллизий.
5. Пример простой реализации поиска пересечений или коллизий с помощью BVH дерева и дискретно-ориентированных многогранников.