Сегодня мы познакомимся с многослойными зеркалами, узнаем, зачем они нужны и как их моделируют при помощи метода матриц переноса.

Обычное зеркало из ванной (и его более качественные собратья) – это ни что иное как тонкая гладкая металлическая пленка. При отражении от нее теряется примерно пять процентов света. Иногда это бывает критично – скажем, в телекоме (чем меньше сигнала теряем, тем меньше ставить промежуточных усилителей) или в сложной оптике типа перископов (если терять на каждом зеркале по 5%, до наблюдателя дойдет очень и очень немного).
С другой стороны, поглощение света на зеркале вызывает его нагрев. И если 5 % от лазерной указки – это что-то эфемерное, то 5 % от промышленного лазера для резки – это около ватта, что может заметно нагреть тонкую пленку. Все еще интереснее у импульсных лазеров, где пиковая мощность достаточна для того, чтобы расплавить зеркало. Примерно вот так:

Наверное, многие слышали про просветление оптики. Это хитрое покрытие линз, позволяющее снизить отражение от их передней поверхности почти до нуля. То есть свет не будет тратиться на отражение, а полностью пойдет в оптическую систему. Физически это происходит за счет деструктивной интерференции от разных слоев просветляющего покрытия.

Бинокль с просветляющим покрытием.
Эту же идею можно использовать в обратную сторону: чтобы отражение не ослаблялось, а наоборот, усиливалось. Нам понадобится слоеный пирог из двух разных материалов, каждый толщиной в четверть длины волны. На каждом из стыков двух материалов часть света отражается назад. Если все отражения, вышедшие наружу, будут иметь одну и ту же фазу, произойдет конструктивная интерференция и отраженный сигнал будет иметь максимально возможную интенсивность.

Такой «слоеный пирог» называют диэлектрическим зеркалом, многослойным зеркалом, или же распределенным брэгговским отражателем (по-английски distributed Bragg reflector, DBR). «Распределенный» он потому, что отражение происходит не на одной поверхности, а сразу на нескольких. Коэффициент отражения может запросто достигать 99.99 %, а значит по сравнению с металлическими зеркалами потери снижаются на 2-3 порядка.
Давайте подробнее посмотрим на схему отражений. Падающий луч отражается назад на каждой из границ двух сред. Правда, каждый отраженный лучик тоже отражается на каждой из границ, которую он проходит по пути назад – теперь уже в другую сторону. Каждый из этих лучиков еще раз отражается… черт, как же их всех сосчитать?
На помощь приходит метод матриц переноса. Суть его в том, что мы перестаем следить за каждым лучиком в отдельности, а смотрим лишь на результат их сложения. То есть мы задаем вектор, описывающий волну в каждой точке.
Вообще говоря, в каждой точке есть две волны: одна распространяется направо (назовем ее ER), вторая – налево (EL). Тогда наш вектор имеет два элемента, причем комплексных: ведь нас интересуют как амплитуда света (модуль числа), так и его фаза (соответственно, фаза числа).
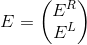
Для любых двух точек вектора будут связаны неким линейным выражением, учитывающим распространение света через среду и через границы двух сред. Записать это выражение можно при помощи матриц. В принципе, нам нужно две матрицы. Первая (назовем ее М1) связывает вектора слева и справа от границы раздела. Вторая (М2) описывает распространение волны в однородной среде (между границами раздела).
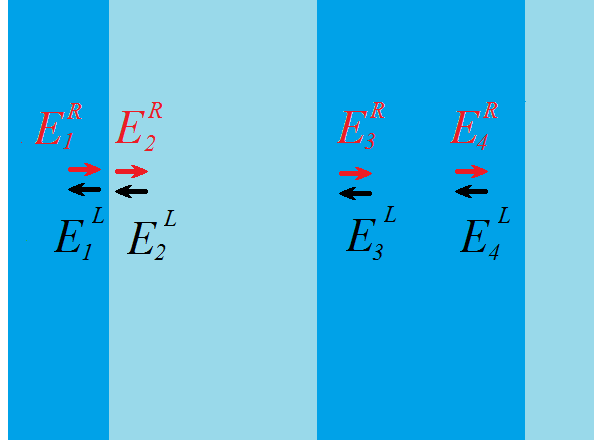
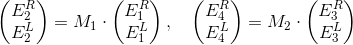
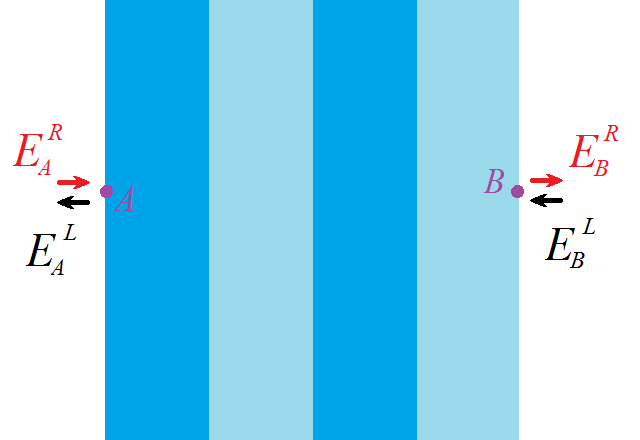
Комбинируя М1 и М2, мы можем связать два вектора в любых точках пространства. Например, между точками А и В на рисунке ниже зависимость будет такая:
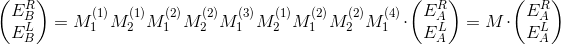
То есть мы просто перемножаем подряд матрицы для всего, через что проходит свет (идет он слева направо):
— граница воздуха и 1 слоя (вход в зеркало)
— распространение в первом слое
— граница 1-2 слоев
— распространение во втором слое
— граница 2-3 слоев
и так далее до выхода из зеркала. И получаем одну матрицу 2х2, описывающую все зеркало сразу!
Я не случайно выбрал точки с двух сторон зеркала. В точке А верхняя компонента вектора (которая летит направо) – это волна, которую мы посылаем на зеркало. Нижняя компонента – это отражение, которое мы хотим посчитать. В точке В (сразу за зеркалом) верхняя компонента – это пропускание зеркала, а нижняя равна нулю потому, что с обратной стороны на зеркало ничего не падает. В итоге получается элементарное матричное уравнение
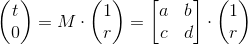
где r и t – отражение и пропускание соответственно. Отсюда, не забывая, что интенсивность – это квадрат амплитуды, получаем отражение
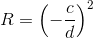
В заключение заметим, что для других длин волн слои будут иметь толщину, отличную от четверти длины волны, поэтому коэффициент отражения может измениться. Чтобы узнать, в каком спектральном диапазоне зеркало будет отражать, придется повторить расчет для разных длин волн.
Код прямолинеен. Для каждой длины волны нужно вычислить М1 и М2, после чего перемножить их нужное количество раз. Так как результаты для разных длин волн независимы, вычисления хорошо параллелятся на многоядерных процессорах. Код, на котором считались примеры ниже, написан на MATLAB’е. Упомяну несколько тонкостей.
1. М1 и М2 для разных длин волн различаются из-за разных показателей преломления (это называется словом дисперсия). Обычно значения показателей преломления табулированы и меняются достаточно гладко, поэтому они хорошо интерполируются полиномом.
Проблема возникает, если начиная с определенной длины волны материал начинает поглощать свет (скажем, так ведут себя полупроводники). Обычно для длины волны, на которой начинается поглощение, хороших табулированных данных нет вообще; а между значениями слева и справа от нее есть разрыв. В этом случае интерполируют отдельно области слева и справа от «плохой» точки, а саму точку игнорируют.
2. Если зеркало состоит из N пар слоев, то вместо вычисления М1 и М2 для каждого слоя можно вычислить их один раз для пары слоев, а потом перемножить их N раз в нужном порядке. Иными словами, сначала посчитать матрицу переноса для пары слоев, а затем возвести ее в N-ую степень. В этом могут здорово помочь полиномы Чебышева.
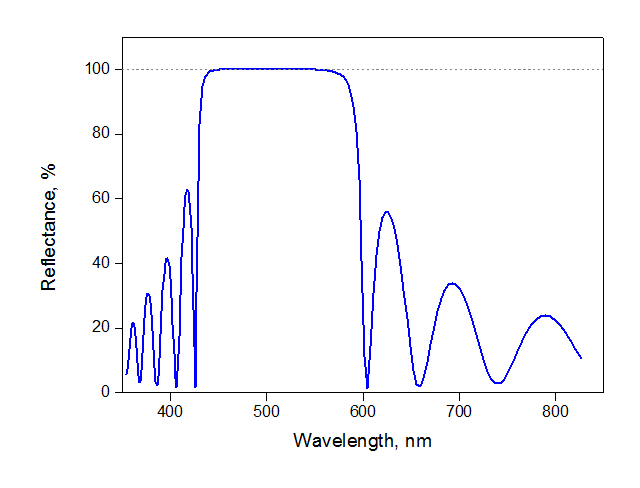
1. Типичный спектр отражения. Простой пример – зеркало из чередующихся слоев TiO2 и SiO2, каждого по 10 раз. Отражение достигает максимума в определенном диапазоне: на картинке – от 420 до 600 нм, то есть наше зеркало работает в сине-зеленой области. Вне рабочего диапазона отражение скачет от нуля до небольших значений; в этих областях зеркалоне совсем совсем не зеркало, а просто бесполезный кусок стекла. В максимуме отражение примерно равно 99.97%.
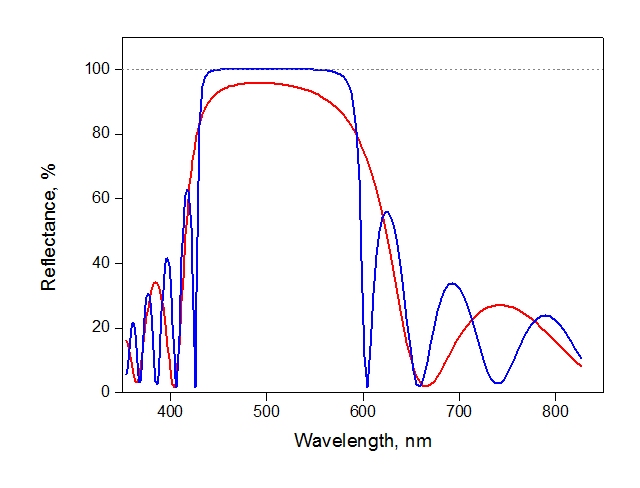
2. Больше слоев – лучше отражение. Кстати, принято считать не слои, а их пары. На картинке ниже красный спектр – 5 пар TiO2/SiO2, синий – 10 пар. На практике не используют слишком много пар, потому что это увеличивает время изготовления. Примерные числа – 5-7 пар для зеркал в обычных лазерных диодах и волоконных лазерах; 20-30 для очень специфичных применений типа квантовой оптики.
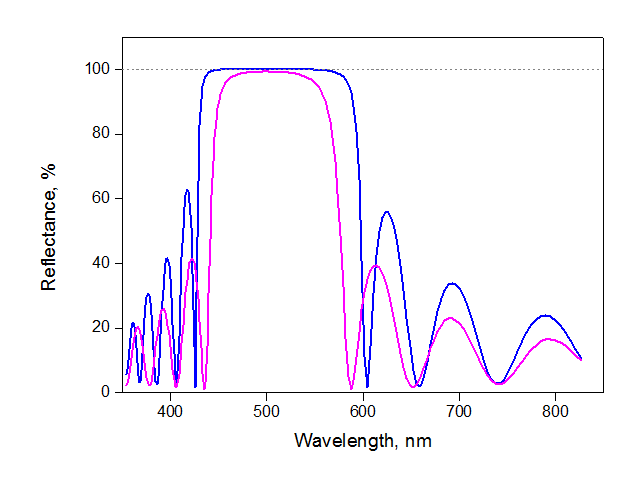
3. Контраст или разница показателей преломления двух материалов. Чем она больше, тем меньше пар нужно для зеркала того же качества. На картинке ниже спектры зеркал из 10 пар TiO2/SiO2 (синий) и ZrO/SiO2 (сиреневый). У последнего разница показателей преломления меньше, поэтому максимальное отражение 99.24% (против 99.97% у TiO2/SiO2) – иными словами, потери в ZrO/SiO2 зеркале в 25 раз больше.
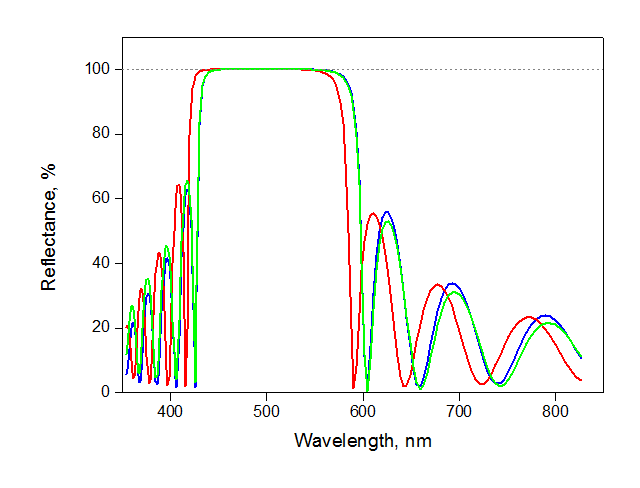
4. Точность изготовления. Слои крайне тонкие (0.1-0.2 микрона), и небольшие отклонения заметно влияют на качество. Для воспроизводимости спектра критично отслеживать не толщину каждого слоя, а толщину пары. Посмотрим, что случится с нашим зеркалом из 10 пар TiO2/SiO2 (синий спектр) при различных ошибках в изготовлении. Если все слои одного материала будут на 10% толще, а второго – на 10% тоньше (зеленый), то толщина пары сохранится неизменной и качество зеркала изменится довольно слабо. В то же время отклонение только одного слоя на 5% меняет толщину пары и заметно сдвигает спектр (красная кривая).
Само собой, в первую очередь метод матриц переноса нужен соответствующим R&D. Лазерные диоды, волоконные лазеры, зеркала (в диапазоне от терагерцовых до мягкого рентгена), узкополосные фильтры и даже просветление оптики считается именно ими.
Дальше, мы видели, что интерференция очень чувствительна к толщине слоев. В принципе, если мы примерно знаем состав некой слоистой структуры, можно определить толщину ее слоев с точностью порядка нанометра. Для этого нужно измерить ее спектр отражения и подогнать его, варьируя толщины слоев в алгоритме. Получается такая система для реверс-инжиниринга слоистых структур. Причем ее стоимость на порядки меньше стоимости электронного микроскопа с таким же разрешением.
Отсюда вытекает еще одно применение – фидбэк на производстве зеркал. Спектр отражения изготовленного зеркала легко померить и сравнить с теоретическим. Если различия существенны, моделирование может показать, что именно пошло не так в техпроцессе. Более того, фидбэк можно получать в реальном времени в процессе изготовления: на напыляемое зеркало светит лампочка, а измеренный спектр отражения выводится на экран.
Формулы выше описывают нормальное отражение (т.е. перпендикулярное зеркалу). В реальности часто нужны зеркала, отражающие под углом. Для таких расчетов алгоритм немного усложняется: приходится добавлять еще один цикл по разным значениям углов.
Чуть сложнее рассчитать вогнутое или выпуклое зеркало: надо отдельно рассматривать разные участки поверхности. Обычно в такой ситуации приходится чем-то жертвовать: спектром, углами отражения, поляризационными свойствами. Эту задачу часто доверяют генетическому алгоритму, настроенному на максимизацию необходимых параметров. Скажем, можно сделать зеркало, отражающее свет подо всеми углами, но спектр и качество будут не лучшими. Или сделать зеркало с отражением около 99.999% – но только для одной длины волны и под одним углом.
Небольшой плюс в том, что необязательно использовать периодическую структуру: толщина слоев может меняться как угодно (такое зеркало называется апериодическим). Можно варьировать сразу десяток толщин – какое раздолье для генетического алгоритма! Именно так рассчитывают зеркала для рентгеновской литографии, которая используется в современных техпроцессах в микроэлектронике.
М. Борн, Э. Вольф «Основы оптики».
На форуме dxdy хорошая заметка про полиномы Чебышева.
Картинки: КДПВ, 1, 2, 3.

Что не так с обычными зеркалами?
Обычное зеркало из ванной (и его более качественные собратья) – это ни что иное как тонкая гладкая металлическая пленка. При отражении от нее теряется примерно пять процентов света. Иногда это бывает критично – скажем, в телекоме (чем меньше сигнала теряем, тем меньше ставить промежуточных усилителей) или в сложной оптике типа перископов (если терять на каждом зеркале по 5%, до наблюдателя дойдет очень и очень немного).
С другой стороны, поглощение света на зеркале вызывает его нагрев. И если 5 % от лазерной указки – это что-то эфемерное, то 5 % от промышленного лазера для резки – это около ватта, что может заметно нагреть тонкую пленку. Все еще интереснее у импульсных лазеров, где пиковая мощность достаточна для того, чтобы расплавить зеркало. Примерно вот так:

Немного физики
Наверное, многие слышали про просветление оптики. Это хитрое покрытие линз, позволяющее снизить отражение от их передней поверхности почти до нуля. То есть свет не будет тратиться на отражение, а полностью пойдет в оптическую систему. Физически это происходит за счет деструктивной интерференции от разных слоев просветляющего покрытия.

Бинокль с просветляющим покрытием.
Эту же идею можно использовать в обратную сторону: чтобы отражение не ослаблялось, а наоборот, усиливалось. Нам понадобится слоеный пирог из двух разных материалов, каждый толщиной в четверть длины волны. На каждом из стыков двух материалов часть света отражается назад. Если все отражения, вышедшие наружу, будут иметь одну и ту же фазу, произойдет конструктивная интерференция и отраженный сигнал будет иметь максимально возможную интенсивность.

Такой «слоеный пирог» называют диэлектрическим зеркалом, многослойным зеркалом, или же распределенным брэгговским отражателем (по-английски distributed Bragg reflector, DBR). «Распределенный» он потому, что отражение происходит не на одной поверхности, а сразу на нескольких. Коэффициент отражения может запросто достигать 99.99 %, а значит по сравнению с металлическими зеркалами потери снижаются на 2-3 порядка.
Немного математики
Давайте подробнее посмотрим на схему отражений. Падающий луч отражается назад на каждой из границ двух сред. Правда, каждый отраженный лучик тоже отражается на каждой из границ, которую он проходит по пути назад – теперь уже в другую сторону. Каждый из этих лучиков еще раз отражается… черт, как же их всех сосчитать?
На помощь приходит метод матриц переноса. Суть его в том, что мы перестаем следить за каждым лучиком в отдельности, а смотрим лишь на результат их сложения. То есть мы задаем вектор, описывающий волну в каждой точке.
Вообще говоря, в каждой точке есть две волны: одна распространяется направо (назовем ее ER), вторая – налево (EL). Тогда наш вектор имеет два элемента, причем комплексных: ведь нас интересуют как амплитуда света (модуль числа), так и его фаза (соответственно, фаза числа).
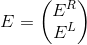
Для любых двух точек вектора будут связаны неким линейным выражением, учитывающим распространение света через среду и через границы двух сред. Записать это выражение можно при помощи матриц. В принципе, нам нужно две матрицы. Первая (назовем ее М1) связывает вектора слева и справа от границы раздела. Вторая (М2) описывает распространение волны в однородной среде (между границами раздела).
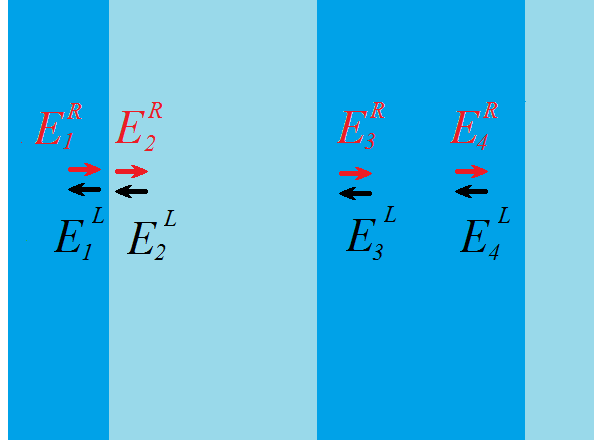
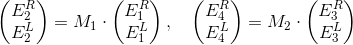
Как все это выводится
Начнем с М1. Представим, что на границу раздела двух сред свет падает с обеих сторон. Для каждого из лучиков мы можем посчитать процент отражения и преломления, а затем сложить результаты. Выражения получаются из формул Френеля. Если бы свет падал только слева (E1R), то отражение и преломление давались бы формулами
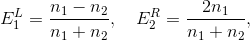
где n1 и n2 – показатели преломления двух сред. Если бы свет падал только справа (E2L), мы бы имели соответственно
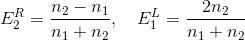
Комбинируя выражения, получаем
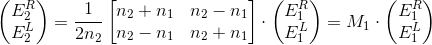
Матрица М2 выглядит гораздо проще. Так как лучи, летящие влево и вправо, не взаимодействуют, матрица диагональна. Амплитуда света не меняется – значит, модуль элементов матрицы равен 1. Изменяется только фаза: у луча, летящего вправо она увеличивается, у летящего влево – уменьшается (знак минус в экспоненте). Получается
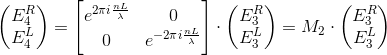
где L – толщина слоя, лямбда – длина волны.
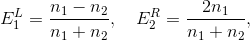
где n1 и n2 – показатели преломления двух сред. Если бы свет падал только справа (E2L), мы бы имели соответственно
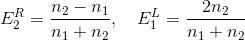
Комбинируя выражения, получаем
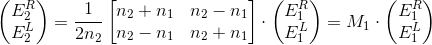
Матрица М2 выглядит гораздо проще. Так как лучи, летящие влево и вправо, не взаимодействуют, матрица диагональна. Амплитуда света не меняется – значит, модуль элементов матрицы равен 1. Изменяется только фаза: у луча, летящего вправо она увеличивается, у летящего влево – уменьшается (знак минус в экспоненте). Получается
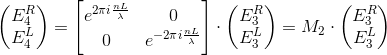
где L – толщина слоя, лямбда – длина волны.
Комбинируя М1 и М2, мы можем связать два вектора в любых точках пространства. Например, между точками А и В на рисунке ниже зависимость будет такая:

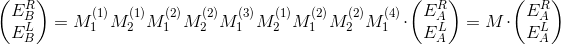
То есть мы просто перемножаем подряд матрицы для всего, через что проходит свет (идет он слева направо):
— граница воздуха и 1 слоя (вход в зеркало)
— распространение в первом слое
— граница 1-2 слоев
— распространение во втором слое
— граница 2-3 слоев
и так далее до выхода из зеркала. И получаем одну матрицу 2х2, описывающую все зеркало сразу!
Я не случайно выбрал точки с двух сторон зеркала. В точке А верхняя компонента вектора (которая летит направо) – это волна, которую мы посылаем на зеркало. Нижняя компонента – это отражение, которое мы хотим посчитать. В точке В (сразу за зеркалом) верхняя компонента – это пропускание зеркала, а нижняя равна нулю потому, что с обратной стороны на зеркало ничего не падает. В итоге получается элементарное матричное уравнение
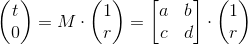
где r и t – отражение и пропускание соответственно. Отсюда, не забывая, что интенсивность – это квадрат амплитуды, получаем отражение
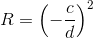
В заключение заметим, что для других длин волн слои будут иметь толщину, отличную от четверти длины волны, поэтому коэффициент отражения может измениться. Чтобы узнать, в каком спектральном диапазоне зеркало будет отражать, придется повторить расчет для разных длин волн.
Код и немного оптимизации
Код прямолинеен. Для каждой длины волны нужно вычислить М1 и М2, после чего перемножить их нужное количество раз. Так как результаты для разных длин волн независимы, вычисления хорошо параллелятся на многоядерных процессорах. Код, на котором считались примеры ниже, написан на MATLAB’е. Упомяну несколько тонкостей.
1. М1 и М2 для разных длин волн различаются из-за разных показателей преломления (это называется словом дисперсия). Обычно значения показателей преломления табулированы и меняются достаточно гладко, поэтому они хорошо интерполируются полиномом.
Проблема возникает, если начиная с определенной длины волны материал начинает поглощать свет (скажем, так ведут себя полупроводники). Обычно для длины волны, на которой начинается поглощение, хороших табулированных данных нет вообще; а между значениями слева и справа от нее есть разрыв. В этом случае интерполируют отдельно области слева и справа от «плохой» точки, а саму точку игнорируют.
2. Если зеркало состоит из N пар слоев, то вместо вычисления М1 и М2 для каждого слоя можно вычислить их один раз для пары слоев, а потом перемножить их N раз в нужном порядке. Иными словами, сначала посчитать матрицу переноса для пары слоев, а затем возвести ее в N-ую степень. В этом могут здорово помочь полиномы Чебышева.
Возведение в степень при помощи полиномов Чебышева.
Пусть M – унимодулярная матрица 2х2 (т.е. детерминант ее равен 1 или -1). Тогда
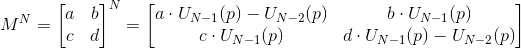
где
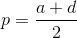 ,
,
a
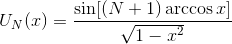
— полиномы Чебышева второго рода.
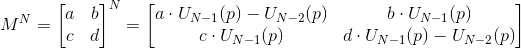
где
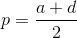 ,
,a
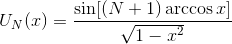
— полиномы Чебышева второго рода.
Интересные результаты
1. Типичный спектр отражения. Простой пример – зеркало из чередующихся слоев TiO2 и SiO2, каждого по 10 раз. Отражение достигает максимума в определенном диапазоне: на картинке – от 420 до 600 нм, то есть наше зеркало работает в сине-зеленой области. Вне рабочего диапазона отражение скачет от нуля до небольших значений; в этих областях зеркало

2. Больше слоев – лучше отражение. Кстати, принято считать не слои, а их пары. На картинке ниже красный спектр – 5 пар TiO2/SiO2, синий – 10 пар. На практике не используют слишком много пар, потому что это увеличивает время изготовления. Примерные числа – 5-7 пар для зеркал в обычных лазерных диодах и волоконных лазерах; 20-30 для очень специфичных применений типа квантовой оптики.

3. Контраст или разница показателей преломления двух материалов. Чем она больше, тем меньше пар нужно для зеркала того же качества. На картинке ниже спектры зеркал из 10 пар TiO2/SiO2 (синий) и ZrO/SiO2 (сиреневый). У последнего разница показателей преломления меньше, поэтому максимальное отражение 99.24% (против 99.97% у TiO2/SiO2) – иными словами, потери в ZrO/SiO2 зеркале в 25 раз больше.

4. Точность изготовления. Слои крайне тонкие (0.1-0.2 микрона), и небольшие отклонения заметно влияют на качество. Для воспроизводимости спектра критично отслеживать не толщину каждого слоя, а толщину пары. Посмотрим, что случится с нашим зеркалом из 10 пар TiO2/SiO2 (синий спектр) при различных ошибках в изготовлении. Если все слои одного материала будут на 10% толще, а второго – на 10% тоньше (зеленый), то толщина пары сохранится неизменной и качество зеркала изменится довольно слабо. В то же время отклонение только одного слоя на 5% меняет толщину пары и заметно сдвигает спектр (красная кривая).

Где это нужно
Само собой, в первую очередь метод матриц переноса нужен соответствующим R&D. Лазерные диоды, волоконные лазеры, зеркала (в диапазоне от терагерцовых до мягкого рентгена), узкополосные фильтры и даже просветление оптики считается именно ими.
Дальше, мы видели, что интерференция очень чувствительна к толщине слоев. В принципе, если мы примерно знаем состав некой слоистой структуры, можно определить толщину ее слоев с точностью порядка нанометра. Для этого нужно измерить ее спектр отражения и подогнать его, варьируя толщины слоев в алгоритме. Получается такая система для реверс-инжиниринга слоистых структур. Причем ее стоимость на порядки меньше стоимости электронного микроскопа с таким же разрешением.
Отсюда вытекает еще одно применение – фидбэк на производстве зеркал. Спектр отражения изготовленного зеркала легко померить и сравнить с теоретическим. Если различия существенны, моделирование может показать, что именно пошло не так в техпроцессе. Более того, фидбэк можно получать в реальном времени в процессе изготовления: на напыляемое зеркало светит лампочка, а измеренный спектр отражения выводится на экран.
Что дальше
Формулы выше описывают нормальное отражение (т.е. перпендикулярное зеркалу). В реальности часто нужны зеркала, отражающие под углом. Для таких расчетов алгоритм немного усложняется: приходится добавлять еще один цикл по разным значениям углов.
Чуть сложнее рассчитать вогнутое или выпуклое зеркало: надо отдельно рассматривать разные участки поверхности. Обычно в такой ситуации приходится чем-то жертвовать: спектром, углами отражения, поляризационными свойствами. Эту задачу часто доверяют генетическому алгоритму, настроенному на максимизацию необходимых параметров. Скажем, можно сделать зеркало, отражающее свет подо всеми углами, но спектр и качество будут не лучшими. Или сделать зеркало с отражением около 99.999% – но только для одной длины волны и под одним углом.
Небольшой плюс в том, что необязательно использовать периодическую структуру: толщина слоев может меняться как угодно (такое зеркало называется апериодическим). Можно варьировать сразу десяток толщин – какое раздолье для генетического алгоритма! Именно так рассчитывают зеркала для рентгеновской литографии, которая используется в современных техпроцессах в микроэлектронике.
Источники
М. Борн, Э. Вольф «Основы оптики».
На форуме dxdy хорошая заметка про полиномы Чебышева.
Картинки: КДПВ, 1, 2, 3.